info
large_stringlengths 120
50k
| question
large_stringlengths 504
10.4k
| avg@8_qwen3_4b_instruct_2507
float64 0
0.88
|
|---|---|---|
{"tests": "{\"inputs\": [\"winlose???winl???w??\\nwin\\n\", \"glo?yto?e??an?\\nor\\n\", \"??c?????\\nabcab\\n\", \"ddddd\\nd\\n\", \"ww?ww\\nw\\n\", \"?????\\nn\\n\", \"xznxr\\nxznxr\\n\", \"wnfbhg?dkhdbh?hdmfjkcunzbh?hdbjjrbh?hddmh?zubhgh?qbjbhghdpwr?bhghdfjnjf?qbhghdqq?qebhgh?umvbhghdivvj\\nbhghd\\n\", \"emnd?t??m?gd?t?p?s??m?dp??t???m?????m?d?ydo????????i??u?d??dp??h??d?tdp???cj?dm?dpxf?hsf??rdmt?pu?tw\\ndmtdp\\n\", \"t?t?t?xnu?\\ntstx\\n\", \"p??p??????\\numpq\\n\", \"irsdljdahusytoclelxidaaiaiaicaiaiaiaiiaiaiyyexmohdwmeyycaiaiaitclluaiaiaiznxweleaiaiaiixdwehyruhizbc\\naiaiai\\n\", \"qjcenuvdsn?ytytyt?yrznaaqeol?tyttyty?ycfaiphfmo?qpvtmhk?xzfr?tytytytytyty?oeqotyt?tyjhdhjtyt?tyyewxh\\ntytyty\\n\", \"zubxnxnxnxn?xixiox?oxinoxnox?xnoxxnox?xnoxixxnox?oxii?xnoxiin?noxixnoxiox?noxixxnox?noxxnoxi?xnoxinn\\nxnoxi\\n\", \"????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????\\nrcmcscoffidfyaeeanevbcfloxrhzxnitikwyidszzgmvicjupbfzhlbkzjbyidpdaeagaanokohwofzvfsvmcwvrqkvgbwnxomajvotbpzqgiyifngpnfvmtsoovrstzhtkeqamskzdmspvihochmajwkdoeozqpkdoxffhokosfqnaqshxbsfnkjsbbkxhrzgqhufq\\n\", \"????ufu\\nfufu\\n\", \"??????c???\\nabcabc\\n\", \"a???????abcax\\naxabcax\\n\", \"cb???????a\\ncbacba\\n\", \"a???????bc\\nabcabc\\n\", \"a????ab\\nabab\\n\", \"pe????????????petooh\\npetoohpetooh\\n\", \"hacking????????????????????????hackingisfun\\nhackingisfunhackingisfun\\n\", \"youdontgiveup????????????????????????????????????youyoudontgiveupdoyo?youyoudontgiveupdoyou\\nyoudontgiveupdoyouyoudontgiveupdoyou\\n\", \"????b?b\\nabab\\n\", \"a\\nb\\n\", \"???a??????a??b?a??a????aabc??a???a?????ab???????b????????????????ab?a?????a????a??a??????b??cb?????????????b?????c????a??????????b????c????????ca?b???????c??bc????????a?b??b??a??cc?b???????a??a?ab?a?ca?a???????c????????b????b?c\\nabaab\\n\", \"????????baaab\\naaabaaab\\n\", \"baaab????????\\nbaaabaaa\\n\", \"??????????????????????????\\nabacaba\\n\", \"ww?ww\\nw\\n\", \"xznxr\\nxznxr\\n\", \"????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????\\nrcmcscoffidfyaeeanevbcfloxrhzxnitikwyidszzgmvicjupbfzhlbkzjbyidpdaeagaanokohwofzvfsvmcwvrqkvgbwnxomajvotbpzqgiyifngpnfvmtsoovrstzhtkeqamskzdmspvihochmajwkdoeozqpkdoxffhokosfqnaqshxbsfnkjsbbkxhrzgqhufq\\n\", \"???a??????a??b?a??a????aabc??a???a?????ab???????b????????????????ab?a?????a????a??a??????b??cb?????????????b?????c????a??????????b????c????????ca?b???????c??bc????????a?b??b??a??cc?b???????a??a?ab?a?ca?a???????c????????b????b?c\\nabaab\\n\", \"a???????bc\\nabcabc\\n\", \"t?t?t?xnu?\\ntstx\\n\", \"zubxnxnxnxn?xixiox?oxinoxnox?xnoxxnox?xnoxixxnox?oxii?xnoxiin?noxixnoxiox?noxixxnox?noxxnoxi?xnoxinn\\nxnoxi\\n\", \"a????ab\\nabab\\n\", \"qjcenuvdsn?ytytyt?yrznaaqeol?tyttyty?ycfaiphfmo?qpvtmhk?xzfr?tytytytytyty?oeqotyt?tyjhdhjtyt?tyyewxh\\ntytyty\\n\", \"hacking????????????????????????hackingisfun\\nhackingisfunhackingisfun\\n\", \"pe????????????petooh\\npetoohpetooh\\n\", \"cb???????a\\ncbacba\\n\", \"????b?b\\nabab\\n\", \"youdontgiveup????????????????????????????????????youyoudontgiveupdoyo?youyoudontgiveupdoyou\\nyoudontgiveupdoyouyoudontgiveupdoyou\\n\", \"????ufu\\nfufu\\n\", \"emnd?t??m?gd?t?p?s??m?dp??t???m?????m?d?ydo????????i??u?d??dp??h??d?tdp???cj?dm?dpxf?hsf??rdmt?pu?tw\\ndmtdp\\n\", \"a\\nb\\n\", \"??????c???\\nabcabc\\n\", \"p??p??????\\numpq\\n\", \"?????\\nn\\n\", \"????????baaab\\naaabaaab\\n\", \"ddddd\\nd\\n\", \"a???????abcax\\naxabcax\\n\", \"irsdljdahusytoclelxidaaiaiaicaiaiaiaiiaiaiyyexmohdwmeyycaiaiaitclluaiaiaiznxweleaiaiaiixdwehyruhizbc\\naiaiai\\n\", \"wnfbhg?dkhdbh?hdmfjkcunzbh?hdbjjrbh?hddmh?zubhgh?qbjbhghdpwr?bhghdfjnjf?qbhghdqq?qebhgh?umvbhghdivvj\\nbhghd\\n\", \"??????????????????????????\\nabacaba\\n\", \"baaab????????\\nbaaabaaa\\n\", \"wv?ww\\nw\\n\", \"rxnzx\\nxznxr\\n\", \"????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????\\nrcmcscoffidfyaeeanevbcfloxrhzxnitikwyddszzgmvicjupbfzhlbkzjbyidpdaeagaanokohwofzvfsvmcwvrqkvgbwnxomajvotbpzqgiyifngpnfvmtsoovrstzhtkeqamskzimspvihochmajwkdoeozqpkdoxffhokosfqnaqshxbsfnkjsbbkxhrzgqhufq\\n\", \"???a??????a??b?a??a????aabc??a???a?????ab???????b????????????????ab?a?????a????a??a??????b??cb?????????????b?????c????a??????????b????c????????ca?b???????c??bc????????a?b??b??a??cc?b???????a??a?ab?a?ca?a???????c????????b????b?c\\nabaac\\n\", \"hxweyyt?tytjhdhjyt?tytoqeo?ytytytytytyt?rfzx?khmtvpq?omfhpiafcy?ytyttyt?loeqaanzry?tytyty?nsdvunecjq\\ntytyty\\n\", \"????b?b\\nbaba\\n\", \"emnd?t??m?gd?t?p?s??m?dp??t???m?????m?d?ydo????????i??u?d??dp??h??d?tdp???cj?dm?dpxf?hsf??rdmt?pu?tw\\ncmtdp\\n\", \"?na??e?oty?olg\\nro\\n\", \"hxweyyt?tytjhdhjyt?tytoqep?ytytytytytyt?rfzx?khmtvpq?omfhpiafcy?ytyttyt?loeqaanzry?tytyty?nsdvunecjq\\nytytyt\\n\", \"a???????bc\\naccabc\\n\", \"t?t?t?xnu?\\ntstw\\n\", \"zubxnxnxnxn?xixiox?oxinoxnox?xnoxxnox?xnoxixxnox?oxii?xnoxiin?noxixnoxiox?noxixxnox?noxxnoxi?xnoxinn\\nixonx\\n\", \"pe????????????petooh\\npetooopetohh\\n\", \"cb???????a\\ncbacbb\\n\", \"youdontgiveup?????????????????????????????u??????youyoudontgiveupdoyo?youyo?dontgiveupdoyou\\nyoudontgiveupdoyouyoudontgiveupdoyou\\n\", \"????ufu\\nfvfu\\n\", \"a\\nc\\n\", \"??????c???\\naacbbc\\n\", \"p??p??????\\nulpq\\n\", \"?????\\nm\\n\", \"ddddd\\ne\\n\", \"wnfbhg?dkhdbh?hdmfjkcunzbh?hdbjjrbh?hddmh?zubhgh?qbjbhghdpwr?bhghdfjnjf?qbhghdqq?qebhgh?umvbhghdivvj\\ndhghb\\n\", \"baaab????????\\nbaabbaaa\\n\", \"?na??e?oty?olg\\nor\\n\", \"??b?????\\nabcab\\n\", \"winlose???winl???w??\\nniw\\n\", \"wv?ww\\nx\\n\", \"rxnzx\\nxxnzr\\n\", \"????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????\\nqfuhqgzrhxkbbsjknfsbxhsqanqfsokohffxodkpqzoeodkwjamhcohivpsmizksmaqekthztsrvoostmvfnpgnfiyigqzpbtovjamoxnwbgvkqrvwcmvsfvzfowhokonaagaeadpdiybjzkblhzfbpujcivmgzzsddywkitinxzhrxolfcbvenaeeayfdiffocscmcr\\n\", \"a???????bc\\nccaabc\\n\", \"t?t??txnu?\\ntstw\\n\", \"zubxnxnxnxn?xixiox?oxinoxnox?xnoxxnox?xnoxixxnox?oxih?xnoxiin?noxixnoxiox?noxixxnox?noxxnoxi?xnoxinn\\nixonx\\n\", \"hxweyyt?tytjhdhjyt?tytoqep?ytytytytytyt?rfzx?khmtvpq?omfhpiafcy?ytyttyt?loeqaanzry?tytyty?nsdvunecjq\\ntytyty\\n\", \"pe????????????petoph\\npetooopetohh\\n\", \"cb???????a\\nbcacbb\\n\", \"youeontgiveup?????????????????????????????u??????youyoudontgiveupdoyo?youyo?dontgiveupdoyou\\nyoudontgiveupdoyouyoudontgiveupdoyou\\n\", \"???u?fu\\nfvfu\\n\", \"wt?up?tmdr??fsh?fxpd?md?jc???pdt?d??h??pd??d?u??i????????ody?d?m?????m???t??pd?m??s?p?t?dg?m??t?dnme\\ncmtdp\\n\", \"??????p??p\\nulpq\\n\", \"ddded\\ne\\n\", \"wnfbhg?dkhdbh?hdmfjkcunzbh?hdbjjrbh?hddmh?zubhgh?qbjbhghdpvr?bhghdfjnjf?qbhghdqq?qebhgh?umvbhghdivvj\\ndhghb\\n\", \"baaab????????\\nbaacbaaa\\n\", \"winlose???winl???w??\\nniv\\n\", \"ww?ww\\nx\\n\", \"rxnzx\\nxynzr\\n\", \"a???????bc\\ncbaacc\\n\", \"t?t??txnu?\\ntstv\\n\", \"zubxnxnxnxn?xixiox?oxinoxnox?xnoxxnox?xnoxixxnox?oxih?xnoxiin?noxixnoxiox?noxixxnox?noxxnoxi?xnoxinn\\nioxnx\\n\", \"pe????????????petoph\\nhhotepoootep\\n\", \"cb???????a\\nbcacba\\n\", \"???u?fu\\nufvf\\n\", \"p??p??????\\nqplu\\n\", \"ddded\\nd\\n\", \"wnfbbg?dkhdbh?hdmfjkcunzbh?hdbjjrbh?hddmh?zubhgh?qhjbhghdpvr?bhghdfjnjf?qbhghdqq?qebhgh?umvbhghdivvj\\ndhghb\\n\", \"baaab????????\\nbaacbaab\\n\", \"glo?yto?e??an?\\nro\\n\", \"winlose???winl???w??\\noiv\\n\", \"ww?ww\\nv\\n\", \"xznxr\\nxynzr\\n\", \"t?t??tynu?\\ntstv\\n\", \"zubxnxnxnxn?xixiox?oxinoxnox?xnoxxnox?xnoxixxnox?oxih?xnoxiin?noxixnoxiox?noxixxnox?noxxnoxi?xnoxinn\\nioxny\\n\", \"glo?yto?e??an?\\nor\\n\", \"??c?????\\nabcab\\n\", \"winlose???winl???w??\\nwin\\n\"], \"outputs\": [\"5\\n\", \"3\\n\", \"2\\n\", \"5\\n\", \"5\\n\", \"5\\n\", \"1\\n\", \"10\\n\", \"11\\n\", \"1\\n\", \"2\\n\", \"6\\n\", \"9\\n\", \"13\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"0\\n\", \"55\\n\", \"2\\n\", \"2\\n\", \"5\\n\", \"5\", \"1\", \"1\", \"55\", \"2\", \"1\", \"13\", \"2\", \"9\", \"2\", \"2\", \"2\", \"2\", \"2\", \"2\", \"11\", \"0\", \"2\", \"2\", \"5\", \"2\", \"5\", \"2\", \"6\", \"10\", \"5\", \"2\", \"4\\n\", \"0\\n\", \"1\\n\", \"34\\n\", \"6\\n\", \"2\\n\", \"5\\n\", \"3\\n\", \"9\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \"5\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"6\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"4\\n\", \"2\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"2\\n\", \"4\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"3\", \"2\", \"5\"]}", "source": "taco"}
|
Berland has a long and glorious history. To increase awareness about it among younger citizens, King of Berland decided to compose an anthem.
Though there are lots and lots of victories in history of Berland, there is the one that stand out the most. King wants to mention it in the anthem as many times as possible.
He has already composed major part of the anthem and now just needs to fill in some letters. King asked you to help him with this work.
The anthem is the string s of no more than 10^5 small Latin letters and question marks. The most glorious victory is the string t of no more than 10^5 small Latin letters. You should replace all the question marks with small Latin letters in such a way that the number of occurrences of string t in string s is maximal.
Note that the occurrences of string t in s can overlap. Check the third example for clarification.
-----Input-----
The first line contains string of small Latin letters and question marks s (1 ≤ |s| ≤ 10^5).
The second line contains string of small Latin letters t (1 ≤ |t| ≤ 10^5).
Product of lengths of strings |s|·|t| won't exceed 10^7.
-----Output-----
Output the maximum number of occurrences of string t you can achieve by replacing all the question marks in string s with small Latin letters.
-----Examples-----
Input
winlose???winl???w??
win
Output
5
Input
glo?yto?e??an?
or
Output
3
Input
??c?????
abcab
Output
2
-----Note-----
In the first example the resulting string s is "winlosewinwinlwinwin"
In the second example the resulting string s is "glorytoreorand". The last letter of the string can be arbitrary.
In the third example occurrences of string t are overlapping. String s with maximal number of occurrences of t is "abcabcab".
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4\\n1 2 4 3\\n\", \"4\\n2 1 4 3\\n\", \"10\\n1 2 10 9 7 4 8 3 6 5\\n\", \"10\\n1 7 10 6 5 2 3 8 9 4\\n\", \"4\\n4 3 2 1\\n\", \"4\\n2 1 3 4\\n\", \"10\\n1 10 9 5 3 2 4 7 8 6\\n\", \"4\\n2 3 1 4\\n\", \"4\\n2 4 3 1\\n\", \"10\\n1 5 10 8 4 3 9 2 7 6\\n\", \"4\\n1 4 3 2\\n\", \"10\\n1 8 10 6 2 4 9 3 7 5\\n\", \"4\\n2 3 4 1\\n\", \"10\\n2 6 10 1 9 7 4 8 5 3\\n\", \"4\\n4 1 2 3\\n\", \"10\\n1 9 10 5 6 7 3 8 4 2\\n\", \"4\\n4 2 1 3\\n\", \"4\\n3 1 4 2\\n\", \"10\\n1 2 3 4 6 5 7 9 10 8\\n\", \"4\\n4 3 1 2\\n\", \"4\\n1 3 4 2\\n\", \"10\\n2 5 10 3 6 4 9 1 8 7\\n\", \"10\\n2 1 10 5 8 4 9 3 7 6\\n\", \"4\\n3 1 2 4\\n\", \"10\\n1 6 10 7 9 5 3 8 4 2\\n\", \"2\\n1 2\\n\", \"10\\n1 3 10 9 4 7 5 8 6 2\\n\", \"4\\n1 3 2 4\\n\", \"4\\n4 2 3 1\\n\", \"4\\n3 2 1 4\\n\", \"4\\n3 2 4 1\\n\", \"4\\n1 2 3 4\\n\", \"10\\n2 7 10 1 6 3 4 8 9 5\\n\", \"2\\n2 1\\n\", \"4\\n3 4 2 1\\n\", \"4\\n3 4 1 2\\n\", \"10\\n10 1 9 2 8 3 7 4 6 5\\n\", \"10\\n1 4 10 8 9 2 3 6 7 5\\n\", \"10\\n2 3 10 5 4 8 6 9 7 1\\n\", \"108\\n1 102 33 99 6 83 4 20 61 100 76 71 44 9 24 87 57 2 81 82 90 85 12 30 66 53 47 36 43 29 31 64 96 84 77 23 93 78 58 68 42 55 13 70 62 19 92 14 10 65 63 75 91 48 11 105 37 50 32 94 18 26 52 89 104 106 86 97 80 95 17 72 40 22 79 103 25 101 35 51 15 98 67 5 34 69 54 27 45 88 56 16 46 60 74 108 21 41 73 39 107 59 3 8 28 49 7 38\\n\", \"4\\n4 1 3 2\\n\", \"4\\n2 4 1 3\\n\", \"10\\n2 4 10 3 9 1 5 7 8 6\\n\", \"4\\n1 4 2 3\\n\", \"3\\n3 2 1\\n\", \"3\\n1 2 3\\n\", \"3\\n2 3 1\\n\"], \"outputs\": [\"2 0\\n\", \"4 0\\n\", \"26 5\\n\", \"26 6\\n\", \"4 1\\n\", \"2 0\\n\", \"20 7\\n\", \"4 0\\n\", \"2 1\\n\", \"26 6\\n\", \"4 0\\n\", \"24 6\\n\", \"0 1\\n\", \"28 1\\n\", \"0 3\\n\", \"26 1\\n\", \"2 3\\n\", \"4 1\\n\", \"6 0\\n\", \"2 2\\n\", \"2 1\\n\", \"28 0\\n\", \"28 0\\n\", \"2 3\\n\", \"24 4\\n\", \"0 0\\n\", \"22 1\\n\", \"2 0\\n\", \"4 1\\n\", \"4 0\\n\", \"2 1\\n\", \"0 0\\n\", \"20 7\\n\", \"0 1\\n\", \"2 2\\n\", \"0 2\\n\", \"24 7\\n\", \"20 5\\n\", \"14 1\\n\", \"3428 30\\n\", \"2 3\\n\", \"2 2\\n\", \"28 0\\n\", \"4 0\\n\", \"2 1\\n\", \"0 0\\n\", \"0 1\\n\"]}", "source": "taco"}
|
Some time ago Mister B detected a strange signal from the space, which he started to study.
After some transformation the signal turned out to be a permutation p of length n or its cyclic shift. For the further investigation Mister B need some basis, that's why he decided to choose cyclic shift of this permutation which has the minimum possible deviation.
Let's define the deviation of a permutation p as <image>.
Find a cyclic shift of permutation p with minimum possible deviation. If there are multiple solutions, print any of them.
Let's denote id k (0 ≤ k < n) of a cyclic shift of permutation p as the number of right shifts needed to reach this shift, for example:
* k = 0: shift p1, p2, ... pn,
* k = 1: shift pn, p1, ... pn - 1,
* ...,
* k = n - 1: shift p2, p3, ... pn, p1.
Input
First line contains single integer n (2 ≤ n ≤ 106) — the length of the permutation.
The second line contains n space-separated integers p1, p2, ..., pn (1 ≤ pi ≤ n) — the elements of the permutation. It is guaranteed that all elements are distinct.
Output
Print two integers: the minimum deviation of cyclic shifts of permutation p and the id of such shift. If there are multiple solutions, print any of them.
Examples
Input
3
1 2 3
Output
0 0
Input
3
2 3 1
Output
0 1
Input
3
3 2 1
Output
2 1
Note
In the first sample test the given permutation p is the identity permutation, that's why its deviation equals to 0, the shift id equals to 0 as well.
In the second sample test the deviation of p equals to 4, the deviation of the 1-st cyclic shift (1, 2, 3) equals to 0, the deviation of the 2-nd cyclic shift (3, 1, 2) equals to 4, the optimal is the 1-st cyclic shift.
In the third sample test the deviation of p equals to 4, the deviation of the 1-st cyclic shift (1, 3, 2) equals to 2, the deviation of the 2-nd cyclic shift (2, 1, 3) also equals to 2, so the optimal are both 1-st and 2-nd cyclic shifts.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.875
|
{"tests": "{\"inputs\": [\"6\\n1 1 1 2 1 1\\n6\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"10\\n5 1 5 1 4 4 2 2 4 4\\n15\\n- 1\\n- 4\\n+ 2\\n+ 2\\n- 5\\n- 5\\n- 4\\n- 4\\n+ 10\\n+ 10\\n+ 10\\n+ 10\\n- 2\\n+ 1\\n- 4\\n\", \"1\\n1\\n34\\n- 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n- 1\\n- 1\\n- 1\\n- 1\\n- 1\\n+ 2\\n+ 2\\n+ 2\\n+ 2\\n- 1\\n+ 2\\n+ 2\\n- 1\\n+ 2\\n- 1\\n+ 3\\n+ 3\\n+ 1\\n- 2\\n- 2\\n- 2\\n- 2\\n+ 1\\n+ 3\\n\", \"11\\n1 1 1 1 1 1 2 2 2 2 2\\n1\\n+ 2\\n\", \"10\\n1 1 1 1 1 1 1 1 1 1\\n1\\n+ 1\\n\", \"12\\n1 1 1 1 2 2 2 2 3 3 3 3\\n1\\n+ 10\\n\", \"5\\n1 1 1 1 1\\n1\\n+ 1\\n\", \"10\\n1 1 1 1 1 1 1 1 1 1\\n1\\n+ 1\\n\", \"1\\n1\\n34\\n- 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n- 1\\n- 1\\n- 1\\n- 1\\n- 1\\n+ 2\\n+ 2\\n+ 2\\n+ 2\\n- 1\\n+ 2\\n+ 2\\n- 1\\n+ 2\\n- 1\\n+ 3\\n+ 3\\n+ 1\\n- 2\\n- 2\\n- 2\\n- 2\\n+ 1\\n+ 3\\n\", \"12\\n1 1 1 1 2 2 2 2 3 3 3 3\\n2\\n+ 3\\n+ 3\\n\", \"11\\n1 1 1 1 1 1 2 2 2 2 2\\n1\\n+ 2\\n\", \"10\\n5 1 5 1 4 4 2 2 4 4\\n15\\n- 1\\n- 4\\n+ 2\\n+ 2\\n- 5\\n- 5\\n- 4\\n- 4\\n+ 10\\n+ 10\\n+ 10\\n+ 10\\n- 2\\n+ 1\\n- 4\\n\", \"12\\n1 1 1 1 2 2 2 2 3 3 3 2\\n1\\n+ 10\\n\", \"1\\n1\\n34\\n- 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n- 1\\n- 1\\n- 1\\n- 1\\n- 1\\n+ 2\\n+ 2\\n+ 2\\n+ 2\\n- 1\\n+ 2\\n+ 2\\n- 1\\n+ 2\\n- 1\\n+ 3\\n+ 3\\n+ 1\\n- 1\\n- 2\\n- 2\\n- 2\\n+ 1\\n+ 3\\n\", \"12\\n1 1 1 1 2 2 2 2 3 0 3 3\\n2\\n+ 3\\n+ 3\\n\", \"6\\n1 1 1 2 1 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"6\\n1 1 1 2 2 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"5\\n1 1 1 2 1\\n1\\n+ 1\\n\", \"1\\n1\\n34\\n- 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n+ 1\\n- 1\\n- 1\\n- 1\\n- 1\\n- 1\\n+ 2\\n+ 2\\n+ 2\\n+ 2\\n- 1\\n+ 2\\n+ 2\\n- 1\\n+ 2\\n- 1\\n+ 4\\n+ 3\\n+ 1\\n- 2\\n- 2\\n- 2\\n- 2\\n+ 1\\n+ 3\\n\", \"6\\n1 1 1 4 1 1\\n6\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"10\\n1 1 1 1 0 1 1 1 1 1\\n1\\n+ 1\\n\", \"11\\n1 0 1 1 1 1 2 2 2 2 2\\n1\\n+ 2\\n\", \"12\\n1 1 1 1 2 2 2 0 3 3 3 2\\n1\\n+ 10\\n\", \"10\\n1 2 1 1 0 1 1 1 1 1\\n1\\n+ 1\\n\", \"11\\n1 0 1 1 1 1 0 2 2 2 2\\n1\\n+ 2\\n\", \"11\\n1 0 1 1 1 2 0 2 2 2 2\\n1\\n+ 2\\n\", \"6\\n0 1 1 2 2 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"11\\n1 0 2 1 1 2 0 2 2 2 2\\n1\\n+ 2\\n\", \"6\\n0 1 1 2 3 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"11\\n1 0 2 1 1 4 0 2 2 2 2\\n1\\n+ 2\\n\", \"6\\n0 0 1 2 3 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"11\\n1 1 2 1 1 4 0 2 2 2 2\\n1\\n+ 2\\n\", \"11\\n1 1 0 1 1 4 0 2 2 2 2\\n1\\n+ 2\\n\", \"11\\n1 1 0 1 1 5 0 2 2 2 2\\n1\\n+ 2\\n\", \"12\\n1 1 1 1 2 2 2 1 3 3 3 3\\n1\\n+ 10\\n\", \"12\\n1 1 1 0 2 2 2 2 3 3 3 3\\n2\\n+ 3\\n+ 3\\n\", \"11\\n1 1 0 1 1 1 2 2 2 2 2\\n1\\n+ 2\\n\", \"12\\n0 1 1 1 2 2 2 2 3 0 3 3\\n2\\n+ 3\\n+ 3\\n\", \"11\\n1 0 0 1 1 1 2 2 2 2 2\\n1\\n+ 2\\n\", \"12\\n1 1 1 1 2 2 2 0 3 3 5 2\\n1\\n+ 10\\n\", \"11\\n1 0 1 1 1 1 0 2 2 1 2\\n1\\n+ 2\\n\", \"6\\n1 1 1 2 2 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 0\\n- 1\\n+ 2\\n\", \"11\\n1 0 1 1 1 2 0 0 2 2 2\\n1\\n+ 2\\n\", \"6\\n0 1 2 2 2 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"11\\n1 0 2 1 1 2 0 2 2 2 2\\n1\\n+ 1\\n\", \"6\\n0 1 1 2 3 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 0\\n\", \"11\\n1 0 2 1 1 2 0 2 0 2 2\\n1\\n+ 2\\n\", \"6\\n0 1 1 2 3 1\\n6\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"11\\n1 1 0 1 1 4 0 2 3 2 2\\n1\\n+ 2\\n\", \"12\\n1 1 1 1 2 2 2 1 3 0 3 3\\n1\\n+ 10\\n\", \"5\\n1 1 1 4 1\\n1\\n+ 1\\n\", \"12\\n1 1 1 0 2 2 2 2 3 3 2 3\\n2\\n+ 3\\n+ 3\\n\", \"11\\n1 1 0 1 1 1 2 2 2 3 2\\n1\\n+ 2\\n\", \"12\\n0 1 1 0 2 2 2 2 3 0 3 3\\n2\\n+ 3\\n+ 3\\n\", \"11\\n1 0 1 1 1 1 0 2 4 1 2\\n1\\n+ 2\\n\", \"6\\n1 1 1 2 1 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 0\\n- 1\\n+ 2\\n\", \"6\\n0 1 2 2 1 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\", \"11\\n1 0 2 1 1 2 0 2 2 2 0\\n1\\n+ 1\\n\", \"11\\n1 1 0 1 1 4 0 2 3 2 2\\n1\\n+ 3\\n\", \"5\\n1 1 1 8 1\\n1\\n+ 1\\n\", \"12\\n1 1 1 0 2 2 2 2 2 3 2 3\\n2\\n+ 3\\n+ 3\\n\", \"11\\n1 1 0 1 1 1 2 2 2 4 2\\n1\\n+ 2\\n\", \"11\\n1 0 1 1 1 1 0 4 4 1 2\\n1\\n+ 2\\n\", \"6\\n0 1 2 2 1 1\\n3\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 2\\n+ 2\\n\", \"11\\n2 0 2 1 1 2 0 2 2 2 0\\n1\\n+ 1\\n\", \"11\\n1 1 0 1 1 4 0 2 3 4 2\\n1\\n+ 3\\n\", \"12\\n1 0 1 0 2 2 2 2 2 3 2 3\\n2\\n+ 3\\n+ 3\\n\", \"11\\n1 1 0 1 1 1 2 2 2 4 2\\n1\\n+ 1\\n\", \"11\\n1 0 0 1 1 1 0 4 4 1 2\\n1\\n+ 2\\n\", \"6\\n0 1 2 2 1 1\\n3\\n+ 2\\n+ 1\\n- 2\\n+ 2\\n- 2\\n+ 2\\n\", \"11\\n1 1 0 1 1 4 0 2 3 4 3\\n1\\n+ 3\\n\", \"12\\n1 0 1 0 2 2 2 2 2 3 2 3\\n1\\n+ 3\\n+ 3\\n\", \"11\\n1 1 1 1 1 1 2 2 2 4 2\\n1\\n+ 1\\n\", \"11\\n1 0 0 1 1 1 1 4 4 1 2\\n1\\n+ 2\\n\", \"6\\n0 1 4 2 1 1\\n3\\n+ 2\\n+ 1\\n- 2\\n+ 2\\n- 2\\n+ 2\\n\", \"12\\n1 0 1 0 3 2 2 2 2 3 2 3\\n1\\n+ 3\\n+ 3\\n\", \"11\\n2 1 1 1 1 1 2 2 2 4 2\\n1\\n+ 1\\n\", \"11\\n1 0 0 1 2 1 1 4 4 1 2\\n1\\n+ 2\\n\", \"6\\n0 1 4 2 1 1\\n3\\n+ 2\\n+ 1\\n- 2\\n* 2\\n- 2\\n+ 2\\n\", \"11\\n2 1 1 1 1 2 2 2 2 4 2\\n1\\n+ 1\\n\", \"11\\n1 0 0 1 2 1 1 4 4 1 1\\n1\\n+ 2\\n\", \"6\\n0 0 4 2 1 1\\n3\\n+ 2\\n+ 1\\n- 2\\n* 2\\n- 2\\n+ 2\\n\", \"11\\n2 1 1 1 1 2 2 2 2 4 1\\n1\\n+ 1\\n\", \"11\\n1 0 0 1 2 1 2 4 4 1 1\\n1\\n+ 2\\n\", \"6\\n0 0 4 2 1 1\\n3\\n+ 2\\n+ 1\\n- 2\\n* 4\\n- 2\\n+ 2\\n\", \"11\\n2 1 0 1 1 2 2 2 2 4 1\\n1\\n+ 1\\n\", \"11\\n1 0 0 1 2 1 2 4 4 0 1\\n1\\n+ 2\\n\", \"11\\n2 1 0 1 1 2 2 4 2 4 1\\n1\\n+ 1\\n\", \"6\\n1 1 1 2 1 1\\n6\\n+ 2\\n+ 1\\n- 1\\n+ 2\\n- 1\\n+ 2\\n\"], \"outputs\": [\"NO\\nYES\\nNO\\nNO\\nNO\\nYES\\n\", \"YES\\nNO\\nNO\\nYES\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nNO\\nYES\\nYES\\n\", \"NO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nYES\\nYES\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nNO\\nNO\\nYES\\nYES\\nYES\\nNO\\nNO\\nYES\\nYES\\nYES\\nYES\\nYES\\nNO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nYES\\nYES\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nNO\\nNO\\nYES\\nYES\\nYES\\nNO\\nNO\\nYES\\nYES\\nYES\\nYES\\nYES\\nNO\\nNO\\nNO\\n\", \"YES\\nYES\\n\", \"YES\\n\", \"YES\\nNO\\nNO\\nYES\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nNO\\nYES\\nYES\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nYES\\nYES\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nNO\\nNO\\nYES\\nYES\\nYES\\nNO\\nNO\\nYES\\nYES\\nYES\\nYES\\nNO\\nNO\\nYES\\nYES\\n\", \"YES\\nYES\\n\", \"NO\\nYES\\nNO\\n\", \"NO\\nNO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nYES\\nYES\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nNO\\nYES\\nNO\\nNO\\nYES\\nYES\\nYES\\nNO\\nNO\\nNO\\nYES\\nYES\\nNO\\nNO\\nNO\\nNO\\nNO\\n\", \"NO\\nNO\\nNO\\nNO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\nYES\\n\", \"YES\\n\", \"YES\\nYES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\nNO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"YES\\nYES\\n\", \"YES\\n\", \"YES\\nYES\\n\", \"YES\\n\", \"NO\\nYES\\nNO\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"YES\\nYES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\nYES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"NO\\nNO\\nNO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\nYES\\nNO\\nNO\\nNO\\nYES\\n\"]}", "source": "taco"}
|
This year in Equestria was a year of plenty, so Applejack has decided to build some new apple storages. According to the advice of the farm designers, she chose to build two storages with non-zero area: one in the shape of a square and another one in the shape of a rectangle (which possibly can be a square as well).
Applejack will build the storages using planks, she is going to spend exactly one plank on each side of the storage. She can get planks from her friend's company. Initially, the company storehouse has $n$ planks, Applejack knows their lengths. The company keeps working so it receives orders and orders the planks itself. Applejack's friend can provide her with information about each operation. For convenience, he will give her information according to the following format:
$+$ $x$: the storehouse received a plank with length $x$ $-$ $x$: one plank with length $x$ was removed from the storehouse (it is guaranteed that the storehouse had some planks with length $x$).
Applejack is still unsure about when she is going to order the planks so she wants to know if she can order the planks to build rectangular and square storages out of them after every event at the storehouse. Applejack is busy collecting apples and she has completely no time to do the calculations so she asked you for help!
We remind you that all four sides of a square are equal, and a rectangle has two pairs of equal sides.
-----Input-----
The first line contains a single integer $n$ ($1 \le n \le 10^5$): the initial amount of planks at the company's storehouse, the second line contains $n$ integers $a_1, a_2, \ldots, a_n$ ($1 \le a_i \le 10^5$): the lengths of the planks.
The third line contains a single integer $q$ ($1 \le q \le 10^5$): the number of events in the company. Each of the next $q$ lines contains a description of the events in a given format: the type of the event (a symbol $+$ or $-$) is given first, then goes the integer $x$ ($1 \le x \le 10^5$).
-----Output-----
After every event in the company, print "YES" if two storages of the required shape can be built from the planks of that company's set, and print "NO" otherwise. You can print each letter in any case (upper or lower).
-----Example-----
Input
6
1 1 1 2 1 1
6
+ 2
+ 1
- 1
+ 2
- 1
+ 2
Output
NO
YES
NO
NO
NO
YES
-----Note-----
After the second event Applejack can build a rectangular storage using planks with lengths $1$, $2$, $1$, $2$ and a square storage using planks with lengths $1$, $1$, $1$, $1$.
After the sixth event Applejack can build a rectangular storage using planks with lengths $2$, $2$, $2$, $2$ and a square storage using planks with lengths $1$, $1$, $1$, $1$.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [\"1 1 1 8\\n\", \"4 2 2 6\\n\", \"3 7 4 6\\n\", \"4 5 1 1\\n\", \"12 12 1 1000\\n\", \"12 1 1000 1000\\n\", \"3 4 701 703\\n\", \"12 12 13 1000000000\\n\", \"3 4 999999999 1000000000\\n\", \"5 6 1000000000 1000000000\\n\", \"1 1 1 1\\n\", \"12 1 100000011 100000024\\n\", \"10 12 220000011 220000032\\n\", \"1 1 1 1000000000\\n\", \"1 1 999999999 1000000000\\n\", \"1 1 1000000000 1000000000\\n\", \"12 12 1 24\\n\", \"12 12 876543210 1000000000\\n\", \"5 11 654321106 654321117\\n\", \"5 11 654321117 654321140\\n\", \"9 12 654321114 654321128\\n\", \"5 12 654321101 654321140\\n\", \"2 12 654321104 654321122\\n\", \"6 1 654321100 654321115\\n\", \"2 1 654321122 654321129\\n\", \"6 2 654321100 654321140\\n\", \"6 2 654321113 654321123\\n\", \"1 7 654321103 654321105\\n\", \"5 3 654321111 654321117\\n\", \"1 3 654321122 654321140\\n\", \"5 8 654321118 654321137\\n\", \"5 8 654321103 654321106\\n\", \"9 8 654321109 654321126\\n\", \"2 2 987654333 987654335\\n\", \"4 8 987654341 987654343\\n\", \"3 12 987654345 987654347\\n\", \"8 1 987654349 987654354\\n\", \"6 8 987654322 987654327\\n\", \"6 10 987654330 987654337\\n\", \"11 4 987654330 987654343\\n\", \"10 7 987654339 987654340\\n\", \"12 12 987654321 987654328\\n\", \"3 10 498103029 647879228\\n\", \"11 3 378541409 796916287\\n\", \"3 3 240953737 404170887\\n\", \"3 8 280057261 834734290\\n\", \"7 8 305686738 573739036\\n\", \"3 8 36348920 167519590\\n\", \"10 2 1 1000000000\\n\", \"4 1 1 100000\\n\", \"2 1 288 300\\n\", \"5 1 1 100\\n\", \"3 3 3 8\\n\", \"5 1 1 100000\\n\", \"5 1 1 1000\\n\", \"6 1 1 10000\\n\", \"12 1 1 100\\n\", \"2 1 1 1000000\\n\", \"10 1 100 1000000000\\n\", \"2 2 7 12\\n\", \"12 1 1 1000\\n\", \"4 1 1 9\\n\", \"5 2 5 1000\\n\", \"3 1 4 10\\n\", \"12 1 1 1000000\\n\", \"10 5 1 1000000000\\n\", \"10 10 1999 3998\\n\", \"3 1 1 1000\\n\", \"10 1 1 21\\n\", \"5 3 15 18\\n\", \"4 4 2 10\\n\", \"6 1 1 10000\\n\", \"2 1 288 300\\n\", \"5 8 654321103 654321106\\n\", \"5 6 1000000000 1000000000\\n\", \"3 4 999999999 1000000000\\n\", \"10 5 1 1000000000\\n\", \"3 3 3 8\\n\", \"12 1 1 1000000\\n\", \"6 2 654321113 654321123\\n\", \"3 8 280057261 834734290\\n\", \"10 1 1 21\\n\", \"4 5 1 1\\n\", \"3 8 36348920 167519590\\n\", \"3 12 987654345 987654347\\n\", \"1 1 1000000000 1000000000\\n\", \"6 10 987654330 987654337\\n\", \"6 1 654321100 654321115\\n\", \"12 12 987654321 987654328\\n\", \"4 1 1 100000\\n\", \"10 12 220000011 220000032\\n\", \"11 4 987654330 987654343\\n\", \"2 1 654321122 654321129\\n\", \"3 4 701 703\\n\", \"9 12 654321114 654321128\\n\", \"3 1 1 1000\\n\", \"3 1 4 10\\n\", \"6 2 654321100 654321140\\n\", \"8 1 987654349 987654354\\n\", \"9 8 654321109 654321126\\n\", \"4 1 1 9\\n\", \"1 1 999999999 1000000000\\n\", \"5 11 654321117 654321140\\n\", \"3 3 240953737 404170887\\n\", \"5 1 1 100000\\n\", \"5 1 1 1000\\n\", \"3 10 498103029 647879228\\n\", \"11 3 378541409 796916287\\n\", \"4 4 2 10\\n\", \"12 12 1 24\\n\", \"12 1 1 100\\n\", \"10 7 987654339 987654340\\n\", \"2 12 654321104 654321122\\n\", \"12 12 13 1000000000\\n\", \"12 12 1 1000\\n\", \"6 8 987654322 987654327\\n\", \"5 3 654321111 654321117\\n\", \"2 2 987654333 987654335\\n\", \"1 1 1 1000000000\\n\", \"12 1 1 1000\\n\", \"1 1 1 1\\n\", \"5 2 5 1000\\n\", \"2 2 7 12\\n\", \"5 11 654321106 654321117\\n\", \"5 3 15 18\\n\", \"5 12 654321101 654321140\\n\", \"5 1 1 100\\n\", \"12 12 876543210 1000000000\\n\", \"10 2 1 1000000000\\n\", \"10 1 100 1000000000\\n\", \"4 8 987654341 987654343\\n\", \"10 10 1999 3998\\n\", \"7 8 305686738 573739036\\n\", \"12 1 100000011 100000024\\n\", \"12 1 1000 1000\\n\", \"5 8 654321118 654321137\\n\", \"1 3 654321122 654321140\\n\", \"1 7 654321103 654321105\\n\", \"2 1 1 1000000\\n\", \"5 10 1000000000 1000000000\\n\", \"10 5 1 1001000000\\n\", \"12 1 1 1100000\\n\", \"1 8 280057261 834734290\\n\", \"10 2 1 21\\n\", \"3 11 36348920 167519590\\n\", \"6 1 541070166 654321115\\n\", \"4 1 1 110000\\n\", \"3 1 701 703\\n\", \"12 12 654321114 654321128\\n\", \"4 2 654321100 654321140\\n\", \"5 2 1 100000\\n\", \"11 3 378541409 1077499882\\n\", \"12 12 13 1000100000\\n\", \"8 2 5 1000\\n\", \"10 2 2 1000000000\\n\", \"4 8 987654341 1462890902\\n\", \"7 5 1 1\\n\", \"3 12 848957522 987654347\\n\", \"2 1 1000000000 1000000000\\n\", \"1 10 987654330 987654337\\n\", \"10 12 370300 220000032\\n\", \"4 1 1 1000\\n\", \"13 1 987654349 987654354\\n\", \"5 21 654321117 654321140\\n\", \"12 12 2 24\\n\", \"5 7 987654339 987654340\\n\", \"12 12 2 1000\\n\", \"6 9 987654322 987654327\\n\", \"2 2 987654333 1718649494\\n\", \"1 1 1 1001000000\\n\", \"5 12 130669505 654321140\\n\", \"5 1 1 110\\n\", \"10 1 100 1000000010\\n\", \"10 1 1999 3998\\n\", \"7 15 305686738 573739036\\n\", \"5 8 654321118 896207631\\n\", \"1 1 654321122 654321140\\n\", \"2 7 654321103 654321105\\n\", \"2 1 1 1001000\\n\", \"4 3 2 6\\n\", \"1 1 1 9\\n\", \"3 7 6 6\\n\", \"10 5 1 1001100000\\n\", \"12 1 2 1100000\\n\", \"4 2 2 6\\n\", \"1 1 1 8\\n\", \"3 7 4 6\\n\"], \"outputs\": [\"2\", \"3\", \"1\", \"1\", \"13\", \"1\", \"3\", \"13\", \"1\", \"1\", \"1\", \"13\", \"11\", \"2\", \"1\", \"1\", \"12\", \"13\", \"4\", \"6\", \"4\", \"6\", \"3\", \"11\", \"3\", \"10\", \"7\", \"2\", \"6\", \"2\", \"6\", \"1\", \"10\", \"2\", \"1\", \"3\", \"6\", \"3\", \"2\", \"12\", \"2\", \"4\", \"4\", \"19\", \"4\", \"4\", \"8\", \"4\", \"18\", \"7\", \"3\", \"9\", \"3\", \"9\", \"9\", \"11\", \"23\", \"3\", \"19\", \"3\", \"23\", \"7\", \"8\", \"4\", \"23\", \"15\", \"11\", \"5\", \"19\", \"3\", \"4\", \"11\\n\", \"3\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"15\\n\", \"3\\n\", \"23\\n\", \"7\\n\", \"4\\n\", \"19\\n\", \"1\\n\", \"4\\n\", \"3\\n\", \"1\\n\", \"2\\n\", \"11\\n\", \"4\\n\", \"7\\n\", \"11\\n\", \"12\\n\", \"3\\n\", \"3\\n\", \"4\\n\", \"5\\n\", \"4\\n\", \"10\\n\", \"6\\n\", \"10\\n\", \"7\\n\", \"1\\n\", \"6\\n\", \"4\\n\", \"9\\n\", \"9\\n\", \"4\\n\", \"19\\n\", \"4\\n\", \"12\\n\", \"23\\n\", \"2\\n\", \"3\\n\", \"13\\n\", \"13\\n\", \"3\\n\", \"6\\n\", \"2\\n\", \"2\\n\", \"23\\n\", \"1\\n\", \"8\\n\", \"3\\n\", \"4\\n\", \"3\\n\", \"6\\n\", \"9\\n\", \"13\\n\", \"18\\n\", \"19\\n\", \"1\\n\", \"11\\n\", \"8\\n\", \"13\\n\", \"1\\n\", \"6\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"1\\n\", \"15\\n\", \"23\\n\", \"2\\n\", \"17\\n\", \"4\\n\", \"11\\n\", \"7\\n\", \"3\\n\", \"9\\n\", \"6\\n\", \"8\\n\", \"19\\n\", \"13\\n\", \"14\\n\", \"18\\n\", \"5\\n\", \"1\\n\", \"4\\n\", \"1\\n\", \"1\\n\", \"11\\n\", \"7\\n\", \"6\\n\", \"6\\n\", \"11\\n\", \"2\\n\", \"13\\n\", \"1\\n\", \"3\\n\", \"2\\n\", \"6\\n\", \"9\\n\", \"19\\n\", \"19\\n\", \"8\\n\", \"6\\n\", \"2\\n\", \"1\\n\", \"3\\n\", \"3\\n\", \"2\\n\", \"1\\n\", \"15\\n\", \"23\\n\", \"3\\n\", \"2\\n\", \"1\\n\"]}", "source": "taco"}
|
Sometimes Mister B has free evenings when he doesn't know what to do. Fortunately, Mister B found a new game, where the player can play against aliens.
All characters in this game are lowercase English letters. There are two players: Mister B and his competitor.
Initially the players have a string s consisting of the first a English letters in alphabetical order (for example, if a = 5, then s equals to "abcde").
The players take turns appending letters to string s. Mister B moves first.
Mister B must append exactly b letters on each his move. He can arbitrary choose these letters. His opponent adds exactly a letters on each move.
Mister B quickly understood that his opponent was just a computer that used a simple algorithm. The computer on each turn considers the suffix of string s of length a and generates a string t of length a such that all letters in the string t are distinct and don't appear in the considered suffix. From multiple variants of t lexicographically minimal is chosen (if a = 4 and the suffix is "bfdd", the computer chooses string t equal to "aceg"). After that the chosen string t is appended to the end of s.
Mister B soon found the game boring and came up with the following question: what can be the minimum possible number of different letters in string s on the segment between positions l and r, inclusive. Letters of string s are numerated starting from 1.
-----Input-----
First and only line contains four space-separated integers: a, b, l and r (1 ≤ a, b ≤ 12, 1 ≤ l ≤ r ≤ 10^9) — the numbers of letters each player appends and the bounds of the segment.
-----Output-----
Print one integer — the minimum possible number of different letters in the segment from position l to position r, inclusive, in string s.
-----Examples-----
Input
1 1 1 8
Output
2
Input
4 2 2 6
Output
3
Input
3 7 4 6
Output
1
-----Note-----
In the first sample test one of optimal strategies generate string s = "abababab...", that's why answer is 2.
In the second sample test string s = "abcdbcaefg..." can be obtained, chosen segment will look like "bcdbc", that's why answer is 3.
In the third sample test string s = "abczzzacad..." can be obtained, chosen, segment will look like "zzz", that's why answer is 1.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"13\\n....LLLLLL...\\n\", \"3\\n.L.\\n\", \"3\\n.R.\\n\", \"4\\n.RL.\\n\", \"17\\n.......RRRRR.....\\n\", \"13\\n...LLLLLL....\\n\", \"17\\n.....RRRRR.......\\n\", \"4\\n..RL\\n\", \"17\\n......RRRRR......\\n\", \"11\\n.RRRLLLLL..\\n\", \"9\\n..RRLL...\\n\"], \"outputs\": [\"10 4\\n\", \"2 1\\n\", \"2 3\\n\", \"2 2\\n\", \"8 13\\n\", \"9 3\\n\", \"6 11\\n\", \"3 3\\n\", \"7 12\\n\", \"2 4\\n\", \"3 4\\n\"]}", "source": "taco"}
|
There is a straight snowy road, divided into n blocks. The blocks are numbered from 1 to n from left to right. If one moves from the i-th block to the (i + 1)-th block, he will leave a right footprint on the i-th block. Similarly, if one moves from the i-th block to the (i - 1)-th block, he will leave a left footprint on the i-th block. If there already is a footprint on the i-th block, the new footprint will cover the old one.
<image>
At the beginning, there were no footprints. Then polar bear Alice starts from the s-th block, makes a sequence of moves and ends in the t-th block. It is known that Alice never moves outside of the road.
You are given the description of Alice's footprints. Your task is to find a pair of possible values of s, t by looking at the footprints.
Input
The first line of the input contains integer n (3 ≤ n ≤ 1000).
The second line contains the description of the road — the string that consists of n characters. Each character will be either "." (a block without footprint), or "L" (a block with a left footprint), "R" (a block with a right footprint).
It's guaranteed that the given string contains at least one character not equal to ".". Also, the first and the last character will always be ".". It's guaranteed that a solution exists.
Output
Print two space-separated integers — the values of s and t. If there are several possible solutions you can print any of them.
Examples
Input
9
..RRLL...
Output
3 4
Input
11
.RRRLLLLL..
Output
7 5
Note
The first test sample is the one in the picture.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[1], [10], [11], [15], [18], [21], [26], [30], [30.49], [35], [100], [1000000], [0], [-3], [null], [\"monkey\"], [[]], [{}]], \"outputs\": [[0.1], [1], [1.07], [1.35], [1.56], [1.75], [2], [2.2], [2.21], [2.35], [4.3], [30001.3], [0], [0], [0], [0], [0], [0]]}", "source": "taco"}
|
Write a function to calculate compound tax using the following table:
For $10 and under, the tax rate should be 10%.
For $20 and under, the tax rate on the first $10 is %10, and the tax on the rest is 7%.
For $30 and under, the tax rate on the first $10 is still %10, the rate for the next $10 is still 7%, and everything else is 5%.
Tack on an additional 3% for the portion of the total above $30.
Return 0 for invalid input(anything that's not a positive real number).
Examples:
An input of 10, should return 1 (1 is 10% of 10)
An input of 21, should return 1.75 (10% of 10 + 7% of 10 + 5% of 1)
* Note that the returned value should be rounded to the nearest penny.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[440], [220], [880], [523.25], [261.625], [1046.5]], \"outputs\": [[\"A\"], [\"A\"], [\"A\"], [\"C\"], [\"C\"], [\"C\"]]}", "source": "taco"}
|
In music, if you double (or halve) the pitch of any note you will get to the same note again.
"Concert A" is fixed at 440 Hz, and every other note is defined based on that. 880 Hz is also an A, as is 1760 Hz, as is 220 Hz.
There are 12 notes in Western music: A, A#, B, C, C#, D, D#, E, F, F#, G, G#. You are given a preloaded dictionary with these 12 notes and one of the pitches that creates that note (starting at Concert A).
Now, given a pitch (in Hz), return the corresponding note. (All inputs will be valid notes).
For reference, the notes dictionary looks like this:
```python
notes_dictionary = {
440: "A",
466.16: "A#",
493.88: "B",
523.25: "C",
554.37: "C#",
587.33: "D",
622.25: "D#",
659.25: "E",
698.46: "F",
739.99: "F#",
783.99: "G",
830.61: "G#"
}
```
Musicians: all pitches based on equal tempermanent, taken from [here](http://pages.mtu.edu/~suits/notefreqs.html).
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.5
|
{"tests": "{\"inputs\": [\"4 5\\n8 8 8 8 8\", \"5 2\\n5 5 6 5\", \"100 3\\n1 3 3\", \"4 5\\n8 8 2 8 8\", \"4 5\\n8 8 2 0 8\", \"4 5\\n8 7 2 0 8\", \"1 5\\n8 7 2 0 8\", \"1 5\\n8 7 4 0 8\", \"0 5\\n8 7 4 0 8\", \"5 4\\n2 7 5 10\", \"0 5\\n8 7 4 0 15\", \"0 5\\n11 7 4 0 15\", \"0 1\\n11 7 4 0 15\", \"5 2\\n1 15 11 10\", \"1 3\\n-1 27 19 0\", \"1 3\\n-2 27 19 0\", \"4 5\\n8 9 8 8 8\", \"0 5\\n8 7 2 0 8\", \"0 5\\n8 7 4 1 8\", \"0 5\\n11 7 4 -1 15\", \"0 2\\n11 7 6 0 6\", \"1 3\\n-1 27 36 0\", \"1 3\\n-2 27 9 0\", \"1 3\\n-2 95 19 0\", \"0 5\\n8 7 3 0 8\", \"1 5\\n8 7 1 0 8\", \"0 0\\n8 7 4 1 8\", \"1 2\\n11 9 6 0 4\", \"0 3\\n1 15 14 1\", \"1 3\\n-2 82 19 0\", \"1 3\\n-2 97 19 0\", \"0 1\\n15 0 -1 -1 1\", \"0 3\\n-2 97 19 0\", \"2 3\\n-2 19 29 0\", \"0 3\\n-2 97 29 0\", \"1 3\\n-2 97 29 0\", \"0 4\\n16 0 6 -1 0\", \"0 3\\n11 7 6 0 10\", \"1 3\\n0 97 29 -1\", \"1 4\\n0 29 8 2\", \"0 4\\n3 2 16 8\", \"0 4\\n3 2 28 6\", \"0 4\\n3 4 28 6\", \"0 1\\n45 -3 -1 1 2\", \"0 4\\n3 4 55 6\", \"0 4\\n3 4 35 6\", \"0 2\\n56 -3 -1 1 2\", \"0 4\\n3 4 35 9\", \"0 4\\n56 -3 0 1 0\", \"0 4\\n56 -3 0 2 0\", \"0 4\\n75 -3 0 0 0\", \"0 1\\n75 -3 0 0 0\", \"5 2\\n3 5 6 5\", \"000 3\\n1 3 3\", \"5 2\\n3 7 6 5\", \"010 3\\n1 3 3\", \"5 2\\n3 7 6 10\", \"010 3\\n1 3 5\", \"5 2\\n2 7 6 10\", \"5 2\\n2 7 5 10\", \"5 4\\n2 7 9 10\", \"5 4\\n2 9 9 10\", \"6 4\\n2 9 9 10\", \"0 1\\n11 7 6 0 15\", \"6 4\\n2 11 9 10\", \"0 1\\n11 7 6 0 17\", \"6 4\\n2 11 11 10\", \"0 1\\n11 7 6 0 27\", \"6 4\\n2 12 11 10\", \"0 1\\n11 7 6 0 3\", \"5 4\\n2 12 11 10\", \"0 1\\n11 7 6 0 6\", \"5 4\\n0 12 11 10\", \"0 1\\n11 7 6 0 2\", \"5 4\\n0 15 11 10\", \"0 1\\n11 9 6 0 2\", \"5 4\\n1 15 11 10\", \"1 1\\n11 9 6 0 2\", \"1 1\\n11 2 6 0 2\", \"5 2\\n1 15 19 10\", \"1 2\\n11 2 6 0 2\", \"5 3\\n1 15 19 10\", \"1 2\\n11 1 6 0 2\", \"5 3\\n1 15 19 1\", \"1 2\\n11 1 6 1 2\", \"5 3\\n0 15 19 1\", \"1 1\\n11 1 6 1 2\", \"5 3\\n0 15 19 0\", \"1 1\\n11 1 6 1 1\", \"5 3\\n0 27 19 0\", \"1 1\\n11 1 6 0 1\", \"5 3\\n-1 27 19 0\", \"1 1\\n11 0 6 0 1\", \"1 1\\n11 0 0 0 1\", \"1 2\\n11 0 0 0 1\", \"1 3\\n-2 50 19 0\", \"1 1\\n9 0 0 0 1\", \"1 1\\n9 0 -1 0 1\", \"2 1\\n9 0 -1 0 1\", \"2 1\\n9 0 -2 0 1\", \"7 5\\n8 8 8 8 8\", \"5 4\\n5 5 6 5\", \"100 3\\n3 3 3\"], \"outputs\": [\"8\\n\", \"2\\n\", \"1\\n\", \"7\\n\", \"6\\n\", \"5\\n\", \"13\\n\", \"14\\n\", \"27\\n\", \"4\\n\", \"34\\n\", \"37\\n\", \"11\\n\", \"3\\n\", \"23\\n\", \"22\\n\", \"9\\n\", \"25\\n\", \"28\\n\", \"36\\n\", \"18\\n\", \"31\\n\", \"17\\n\", \"56\\n\", \"26\\n\", \"12\\n\", \"0\\n\", \"10\\n\", \"30\\n\", \"50\\n\", \"57\\n\", \"15\\n\", \"114\\n\", \"16\\n\", \"124\\n\", \"62\\n\", \"21\\n\", \"24\\n\", \"63\\n\", \"20\\n\", \"29\\n\", \"39\\n\", \"41\\n\", \"45\\n\", \"68\\n\", \"48\\n\", \"53\\n\", \"51\\n\", \"54\\n\", \"55\\n\", \"72\\n\", \"75\\n\", \"2\\n\", \"7\\n\", \"2\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"5\\n\", \"5\\n\", \"5\\n\", \"11\\n\", \"5\\n\", \"11\\n\", \"5\\n\", \"11\\n\", \"5\\n\", \"11\\n\", \"6\\n\", \"11\\n\", \"6\\n\", \"11\\n\", \"6\\n\", \"11\\n\", \"7\\n\", \"6\\n\", \"6\\n\", \"3\\n\", \"7\\n\", \"6\\n\", \"6\\n\", \"6\\n\", \"6\\n\", \"6\\n\", \"6\\n\", \"6\\n\", \"6\\n\", \"8\\n\", \"6\\n\", \"8\\n\", \"6\\n\", \"6\\n\", \"6\\n\", \"34\\n\", \"5\\n\", \"5\\n\", \"3\\n\", \"3\\n\", \"5\", \"4\", \"1\"]}", "source": "taco"}
|
I’m planning to have a party on my birthday. Many of my friends will come to the party. Some of them will come with one or more pieces of cakes, but it is not certain if the number of the cakes is a multiple of the number of people coming.
I wish to enjoy the cakes equally among the partiers. So, I decided to apply the following rules. First, all the party attendants are given the same number of cakes. If some remainder occurs, a piece goes on a priority basis to the party host (that’s me!). How many pieces of cake can I enjoy?
Given the number of my friends and cake information, make a program to calculate how many pieces of cake I can enjoy. Note that I am not counted in the number of my friends.
Input
The input is given in the following format.
$N$ $C$
$p_1$ $p_2$ ... $p_C$
The first line provides the number of my friends $N$ ($1 \leq N \leq 100$) and the number of those among them who brought one or more pieces of cake with them $C$ ($1 \leq C \leq N$). The second line provides an array of integers $p_i$ ($1 \leq p_i \leq100$), each of which shows the number of cakes of the $i$-th friend of mine who was willing to come up with one or more pieces of cake.
Output
Output the number of cakes I can enjoy.
Examples
Input
5 4
5 5 6 5
Output
4
Input
7 5
8 8 8 8 8
Output
5
Input
100 3
3 3 3
Output
1
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\\n1 2\\n3 4\\n5 6\\n\", \"3\\n1010 10\\n1000 1\\n20 1020\\n\", \"2\\n1 1\\n1000000000 1000000000\\n\", \"2\\n1 1\\n1000000000 1000000100\", \"3\\n1 2\\n3 4\\n3 6\", \"3\\n1010 10\\n1000 1\\n20 294\", \"2\\n1 1\\n1000000000 1000100100\", \"3\\n1010 10\\n1000 1\\n26 294\", \"3\\n1 2\\n3 4\\n3 9\", \"3\\n1010 10\\n1000 1\\n50 294\", \"3\\n0 2\\n3 4\\n3 9\", \"3\\n1010 10\\n0000 1\\n50 294\", \"3\\n1010 0\\n0000 1\\n50 294\", \"3\\n1011 0\\n0000 1\\n50 294\", \"2\\n1 1\\n1100000000 1000000000\", \"3\\n1 2\\n3 4\\n5 3\", \"3\\n1011 10\\n1000 1\\n20 1020\", \"3\\n1011 10\\n1000 1\\n20 294\", \"2\\n1 1\\n1000000000 1000100000\", \"3\\n1 2\\n3 3\\n5 6\", \"3\\n1 3\\n3 4\\n3 9\", \"3\\n1110 10\\n1000 1\\n50 294\", \"3\\n0 2\\n3 4\\n0 9\", \"3\\n1010 0\\n0000 1\\n91 294\", \"3\\n1011 0\\n0100 1\\n50 294\", \"2\\n1 1\\n1100000000 1000001000\", \"3\\n1 4\\n3 4\\n5 3\", \"3\\n1011 10\\n1000 2\\n20 1020\", \"3\\n1011 10\\n1000 1\\n20 108\", \"2\\n1 1\\n1000000010 1000100000\", \"3\\n1110 10\\n1001 1\\n26 294\", \"3\\n1110 0\\n1000 1\\n50 294\", \"3\\n0 2\\n1 4\\n0 9\", \"3\\n1110 0\\n0000 1\\n91 294\", \"3\\n1011 0\\n0101 1\\n50 294\", \"3\\n1010 0\\n0001 1\\n77 279\", \"3\\n2 2\\n6 4\\n1 6\", \"3\\n1111 10\\n1000 1\\n20 108\", \"2\\n1 1\\n1000000010 1000101000\", \"3\\n1110 10\\n1001 1\\n33 294\", \"3\\n0110 0\\n1000 1\\n50 294\", \"3\\n1111 0\\n0000 1\\n91 294\", \"3\\n1010 1\\n0001 1\\n77 279\", \"3\\n1011 3\\n1000 2\\n24 1020\", \"3\\n1101 10\\n1000 1\\n20 108\", \"2\\n1 1\\n1000000010 0000100000\", \"3\\n1110 10\\n1001 1\\n29 294\", \"3\\n1110 -1\\n1000 1\\n50 294\", \"3\\n1010 19\\n0000 0\\n40 519\", \"3\\n1111 0\\n0000 1\\n138 294\", \"3\\n1111 0\\n0101 1\\n29 294\", \"3\\n1010 1\\n0101 1\\n77 279\", \"3\\n1011 3\\n1100 2\\n24 1020\", \"3\\n1 4\\n6 4\\n1 6\", \"3\\n1101 10\\n1000 1\\n20 192\", \"3\\n1111 10\\n1001 1\\n29 294\", \"3\\n1110 -1\\n1000 1\\n50 115\", \"3\\n1010 19\\n0000 0\\n9 519\", \"3\\n1111 -1\\n0000 1\\n138 294\", \"3\\n1111 1\\n0101 1\\n29 294\", \"3\\n1010 1\\n0101 1\\n153 279\", \"3\\n2 4\\n6 4\\n8 0\", \"3\\n1010 3\\n1100 2\\n24 1020\", \"3\\n1101 0\\n1000 1\\n20 192\", \"3\\n1111 10\\n1001 1\\n29 296\", \"3\\n1110 -1\\n1000 1\\n67 115\", \"3\\n0000 15\\n1110 1\\n50 294\", \"3\\n2 4\\n12 4\\n8 0\", \"3\\n1010 3\\n0100 2\\n24 1020\", \"3\\n1101 10\\n1001 1\\n29 296\", \"3\\n1110 0\\n1000 1\\n67 115\", \"3\\n1010 22\\n0000 1\\n9 519\", \"3\\n1111 -2\\n0000 1\\n138 186\", \"3\\n1111 1\\n0101 0\\n16 294\", \"3\\n1010 1\\n0101 0\\n153 323\", \"3\\n1010 3\\n0101 2\\n24 1020\", \"3\\n1101 0\\n1000 0\\n20 202\", \"3\\n1101 10\\n1001 1\\n29 105\", \"3\\n0000 15\\n1010 1\\n44 294\", \"3\\n1010 22\\n0100 1\\n9 519\", \"3\\n1111 -2\\n0000 2\\n138 186\", \"3\\n1111 1\\n0101 -1\\n16 294\", \"3\\n1 2\\n8 5\\n1 7\", \"3\\n1101 0\\n1000 0\\n20 303\", \"3\\n0101 10\\n1001 1\\n29 105\", \"3\\n1110 0\\n1100 1\\n67 27\", \"3\\n0000 15\\n1000 1\\n44 294\", \"3\\n0010 22\\n0100 1\\n9 519\", \"3\\n1111 -2\\n0000 2\\n27 186\", \"3\\n1111 1\\n0101 -1\\n16 95\", \"3\\n1010 2\\n0101 0\\n217 323\", \"3\\n1010 6\\n0101 2\\n24 1863\", \"3\\n1101 0\\n1000 0\\n20 377\", \"3\\n0101 10\\n1001 1\\n50 105\", \"3\\n0000 15\\n1010 1\\n83 294\", \"3\\n1111 -2\\n0100 2\\n27 186\", \"3\\n1111 1\\n0101 -1\\n18 95\", \"3\\n1010 2\\n0101 0\\n151 323\", \"3\\n1010 6\\n0101 2\\n18 1863\", \"3\\n1101 0\\n0000 0\\n20 377\", \"3\\n-1 0\\n1 2\\n1 9\", \"3\\n0001 15\\n1010 1\\n83 294\", \"3\\n0011 22\\n0110 1\\n9 519\", \"2\\n1 1\\n1000000000 1000000000\", \"3\\n1 2\\n3 4\\n5 6\", \"3\\n1010 10\\n1000 1\\n20 1020\"], \"outputs\": [\"15\\n\", \"380\\n\", \"999999998000000001\\n\", \"1000000097999999901\\n\", \"5\\n\", \"13604\\n\", \"1000100097999899901\\n\", \"17900\\n\", \"8\\n\", \"35084\\n\", \"9\\n\", \"49490\\n\", \"50450\\n\", \"50500\\n\", \"1099999997900000001\\n\", \"4\\n\", \"380\\n\", \"13623\\n\", \"1000099997999900001\\n\", \"15\\n\", \"0\\n\", \"39984\\n\", \"21\\n\", \"91819\\n\", \"45550\\n\", \"1100001097899999001\\n\", \"2\\n\", \"360\\n\", \"17157\\n\", \"1000100008000899991\\n\", \"20400\\n\", \"40800\\n\", \"7\\n\", \"100919\\n\", \"45500\\n\", \"77693\\n\", \"12\\n\", \"19057\\n\", \"1000101008000908991\\n\", \"26112\\n\", \"44500\\n\", \"101010\\n\", \"76684\\n\", \"440\\n\", \"18867\\n\", \"99999000899991\\n\", \"22848\\n\", \"41616\\n\", \"40400\\n\", \"153180\\n\", \"29290\\n\", \"69084\\n\", \"1958\\n\", \"6\\n\", \"17271\\n\", \"22876\\n\", \"50745\\n\", \"19190\\n\", \"154290\\n\", \"28280\\n\", \"138168\\n\", \"16\\n\", \"1980\\n\", \"18180\\n\", \"22820\\n\", \"67660\\n\", \"54390\\n\", \"32\\n\", \"20240\\n\", \"22540\\n\", \"66665\\n\", \"21210\\n\", \"155400\\n\", \"16160\\n\", \"139077\\n\", \"20218\\n\", \"17980\\n\", \"27888\\n\", \"43430\\n\", \"19110\\n\", \"155260\\n\", \"17170\\n\", \"24\\n\", \"15960\\n\", \"25200\\n\", \"28161\\n\", \"43000\\n\", \"4473\\n\", \"32161\\n\", \"17272\\n\", \"197253\\n\", \"38764\\n\", \"14480\\n\", \"44100\\n\", \"82585\\n\", \"29319\\n\", \"19304\\n\", \"137259\\n\", \"28192\\n\", \"22020\\n\", \"10\\n\", \"81590\\n\", \"4970\\n\", \"999999998000000001\", \"15\", \"380\"]}", "source": "taco"}
|
There are N bags, each containing two white balls. The i-th box contains two balls with integers x_i and y_i written on them, respectively.
For each of these bags, you will paint one of the balls red, and paint the other blue.
Afterwards, the 2N balls will be classified according to color.
Then, we will define the following:
- R_{max}: the maximum integer written on a ball painted in red
- R_{min}: the minimum integer written on a ball painted in red
- B_{max}: the maximum integer written on a ball painted in blue
- B_{min}: the minimum integer written on a ball painted in blue
Find the minimum possible value of (R_{max} - R_{min}) \times (B_{max} - B_{min}).
-----Constraints-----
- 1 ≤ N ≤ 200,000
- 1 ≤ x_i, y_i ≤ 10^9
-----Input-----
Input is given from Standard Input in the following format:
N
x_1 y_1
x_2 y_2
:
x_N y_N
-----Output-----
Print the minimum possible value.
-----Sample Input-----
3
1 2
3 4
5 6
-----Sample Output-----
15
The optimal solution is to paint the balls with x_1, x_2, y_3 red, and paint the balls with y_1, y_2, x_3 blue.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [\"3\\n3 1\\n2 1\\n4 0\\n\", \"5\\n200000 200000\\n24567 23423\\n1 200000\\n200000 1\\n200000 0\\n\", \"5\\n2 200000\\n199991 200000\\n100000 1024\\n1024 0\\n200000 2048\\n\", \"5\\n199991 200000\\n199992 200000\\n199992 200000\\n199992 200000\\n199996 200000\\n\", \"5\\n200000 200000\\n200000 200000\\n200000 200000\\n200000 200000\\n200000 200000\\n\", \"5\\n60522 167713\\n36426 133836\\n48772 148202\\n133447 125228\\n103497 63591\\n\", \"5\\n60522 200000\\n36426 200000\\n48772 200000\\n133447 200000\\n103497 200000\\n\", \"5\\n22 167713\\n26 133836\\n72 148202\\n47 125228\\n97 63591\\n\", \"5\\n22 59\\n26 60\\n72 72\\n47 3\\n97 16\\n\", \"5\\n22 578\\n26 604\\n72 839\\n47 857\\n97 400\\n\", \"5\\n522 1981\\n426 1890\\n772 1010\\n1447 1859\\n1497 1362\\n\", \"5\\n522 3161\\n426 3209\\n772 2238\\n1447 1372\\n3497 3893\\n\", \"5\\n2522 4467\\n426 3791\\n772 4195\\n1447 2006\\n5497 2673\\n\", \"5\\n4522 2314\\n4426 2886\\n772 5081\\n5447 5120\\n7497 7239\\n\", \"5\\n522 1278\\n6426 4981\\n8772 2685\\n3447 3137\\n3497 8752\\n\", \"5\\n8522 11028\\n426 7666\\n772 1884\\n1447 9437\\n11497 840\\n\", \"5\\n12522 19\\n6426 11199\\n10772 1658\\n3447 5303\\n3497 2454\\n\", \"5\\n4522 7771\\n4426 15425\\n772 9303\\n13447 13626\\n15497 8407\\n\", \"5\\n8522 3000\\n6426 17386\\n6772 11564\\n1447 9637\\n5497 16252\\n\", \"5\\n522 2785\\n16426 4821\\n8772 9458\\n13447 4313\\n3497 17838\\n\", \"5\\n14522 5674\\n16426 10901\\n10772 1084\\n15447 20499\\n17497 3424\\n\", \"5\\n20522 18433\\n12426 1766\\n772 12777\\n13447 20072\\n23497 22354\\n\", \"5\\n6522 1207\\n12426 6846\\n2772 4748\\n17447 20123\\n5497 2514\\n\", \"5\\n12522 27839\\n20426 6881\\n24772 26346\\n17447 22381\\n3497 17251\\n\", \"5\\n20522 18989\\n6426 23733\\n18772 19072\\n13447 4385\\n23497 10041\\n\", \"5\\n20522 2314\\n4426 7311\\n16772 25205\\n13447 30239\\n15497 27795\\n\", \"5\\n522 8443\\n8426 120\\n6772 32508\\n5447 9690\\n23497 31112\\n\", \"5\\n8522 19723\\n24426 317\\n24772 34\\n1447 2271\\n23497 29933\\n\", \"5\\n20522 9466\\n18426 17637\\n16772 16118\\n35447 22061\\n23497 36309\\n\", \"5\\n20522 12967\\n36426 14501\\n8772 19546\\n13447 38726\\n23497 3234\\n\", \"5\\n26522 28224\\n6426 4535\\n24772 21028\\n31447 35982\\n17497 28737\\n\", \"5\\n36522 17830\\n16426 33675\\n32772 1463\\n37447 18818\\n39497 38127\\n\", \"5\\n18522 39204\\n30426 32870\\n32772 13018\\n7447 37823\\n5497 27005\\n\", \"5\\n20522 15275\\n36426 23993\\n772 4851\\n13447 47491\\n47497 10125\\n\", \"5\\n10522 49291\\n36426 49737\\n48772 14993\\n33447 42227\\n3497 6588\\n\", \"5\\n32522 22058\\n12426 18213\\n28772 45814\\n17447 46926\\n31497 1982\\n\", \"5\\n26522 46763\\n24426 20644\\n42772 46922\\n1447 50380\\n23497 32679\\n\", \"5\\n12522 2866\\n20426 46782\\n24772 15392\\n45447 8381\\n31497 32520\\n\", \"5\\n46522 40903\\n2426 51978\\n6772 5583\\n43447 16967\\n5497 14176\\n\", \"5\\n20522 4881\\n36426 45854\\n48772 33403\\n13447 20564\\n23497 16268\\n\", \"5\\n12522 3232\\n24426 29310\\n38772 39110\\n55447 18296\\n15497 9786\\n\", \"5\\n52522 10077\\n4426 42688\\n16772 59779\\n13447 55100\\n47497 39698\\n\", \"5\\n14522 43036\\n60426 4985\\n54772 28204\\n37447 11075\\n17497 16728\\n\", \"5\\n522 28717\\n8426 35475\\n40772 49700\\n5447 42746\\n23497 29250\\n\", \"5\\n40522 32643\\n6426 10515\\n38772 15930\\n3447 27180\\n3497 49771\\n\", \"5\\n44522 55545\\n60426 6915\\n24772 6685\\n37447 10900\\n23497 34907\\n\", \"5\\n4522 31786\\n2426 2907\\n66772 47\\n5447 64736\\n47497 48777\\n\", \"5\\n20522 53736\\n56426 4658\\n16772 40371\\n73447 29991\\n23497 62948\\n\", \"5\\n32522 70109\\n12426 71675\\n54772 11619\\n43447 61148\\n5497 59767\\n\", \"5\\n20522 27100\\n36426 19806\\n48772 30101\\n13447 72881\\n63497 20955\\n\", \"5\\n26522 80986\\n62426 38438\\n76772 37666\\n43447 27239\\n13497 10653\\n\", \"5\\n68522 77585\\n48426 29779\\n24772 57939\\n73447 34586\\n59497 1126\\n\", \"5\\n28522 21694\\n40426 71172\\n52772 47783\\n61447 31928\\n27497 72150\\n\", \"5\\n36522 6298\\n60426 65175\\n32772 49609\\n37447 40527\\n39497 68728\\n\", \"5\\n80522 13536\\n6426 18454\\n78772 78078\\n73447 880\\n23497 82319\\n\", \"5\\n64522 50719\\n76426 17985\\n32772 22133\\n53447 62282\\n51497 50268\\n\", \"5\\n48522 65231\\n22426 75375\\n66772 58717\\n17447 24560\\n55497 76940\\n\", \"5\\n20522 53850\\n36426 13980\\n48772 85787\\n13447 69672\\n47497 92782\\n\", \"5\\n68522 72136\\n62426 69558\\n38772 16169\\n31447 52010\\n17497 84468\\n\", \"5\\n60522 34392\\n36426 92971\\n48772 47765\\n33447 90408\\n3497 41078\\n\", \"1\\n1 0\\n\", \"5\\n10522 49291\\n36426 49737\\n48772 14993\\n33447 42227\\n3497 6588\\n\", \"5\\n26522 28224\\n6426 4535\\n24772 21028\\n31447 35982\\n17497 28737\\n\", \"5\\n40522 32643\\n6426 10515\\n38772 15930\\n3447 27180\\n3497 49771\\n\", \"5\\n20522 18989\\n6426 23733\\n18772 19072\\n13447 4385\\n23497 10041\\n\", \"5\\n20522 18433\\n12426 1766\\n772 12777\\n13447 20072\\n23497 22354\\n\", \"5\\n32522 70109\\n12426 71675\\n54772 11619\\n43447 61148\\n5497 59767\\n\", \"5\\n60522 34392\\n36426 92971\\n48772 47765\\n33447 90408\\n3497 41078\\n\", \"5\\n20522 9466\\n18426 17637\\n16772 16118\\n35447 22061\\n23497 36309\\n\", \"5\\n20522 53850\\n36426 13980\\n48772 85787\\n13447 69672\\n47497 92782\\n\", \"5\\n68522 77585\\n48426 29779\\n24772 57939\\n73447 34586\\n59497 1126\\n\", \"5\\n26522 80986\\n62426 38438\\n76772 37666\\n43447 27239\\n13497 10653\\n\", \"5\\n22 59\\n26 60\\n72 72\\n47 3\\n97 16\\n\", \"5\\n36522 6298\\n60426 65175\\n32772 49609\\n37447 40527\\n39497 68728\\n\", \"5\\n52522 10077\\n4426 42688\\n16772 59779\\n13447 55100\\n47497 39698\\n\", \"5\\n522 8443\\n8426 120\\n6772 32508\\n5447 9690\\n23497 31112\\n\", \"5\\n8522 3000\\n6426 17386\\n6772 11564\\n1447 9637\\n5497 16252\\n\", \"5\\n26522 46763\\n24426 20644\\n42772 46922\\n1447 50380\\n23497 32679\\n\", \"5\\n2522 4467\\n426 3791\\n772 4195\\n1447 2006\\n5497 2673\\n\", \"5\\n48522 65231\\n22426 75375\\n66772 58717\\n17447 24560\\n55497 76940\\n\", \"5\\n522 1278\\n6426 4981\\n8772 2685\\n3447 3137\\n3497 8752\\n\", \"5\\n64522 50719\\n76426 17985\\n32772 22133\\n53447 62282\\n51497 50268\\n\", \"5\\n20522 15275\\n36426 23993\\n772 4851\\n13447 47491\\n47497 10125\\n\", \"5\\n8522 19723\\n24426 317\\n24772 34\\n1447 2271\\n23497 29933\\n\", \"5\\n14522 43036\\n60426 4985\\n54772 28204\\n37447 11075\\n17497 16728\\n\", \"5\\n46522 40903\\n2426 51978\\n6772 5583\\n43447 16967\\n5497 14176\\n\", \"5\\n60522 200000\\n36426 200000\\n48772 200000\\n133447 200000\\n103497 200000\\n\", \"5\\n522 1981\\n426 1890\\n772 1010\\n1447 1859\\n1497 1362\\n\", \"5\\n4522 31786\\n2426 2907\\n66772 47\\n5447 64736\\n47497 48777\\n\", \"5\\n200000 200000\\n24567 23423\\n1 200000\\n200000 1\\n200000 0\\n\", \"5\\n12522 19\\n6426 11199\\n10772 1658\\n3447 5303\\n3497 2454\\n\", \"5\\n28522 21694\\n40426 71172\\n52772 47783\\n61447 31928\\n27497 72150\\n\", \"5\\n18522 39204\\n30426 32870\\n32772 13018\\n7447 37823\\n5497 27005\\n\", \"5\\n22 167713\\n26 133836\\n72 148202\\n47 125228\\n97 63591\\n\", \"5\\n14522 5674\\n16426 10901\\n10772 1084\\n15447 20499\\n17497 3424\\n\", \"5\\n68522 72136\\n62426 69558\\n38772 16169\\n31447 52010\\n17497 84468\\n\", \"1\\n1 0\\n\", \"5\\n12522 27839\\n20426 6881\\n24772 26346\\n17447 22381\\n3497 17251\\n\", \"5\\n12522 3232\\n24426 29310\\n38772 39110\\n55447 18296\\n15497 9786\\n\", \"5\\n8522 11028\\n426 7666\\n772 1884\\n1447 9437\\n11497 840\\n\", \"5\\n20522 27100\\n36426 19806\\n48772 30101\\n13447 72881\\n63497 20955\\n\", \"5\\n522 28717\\n8426 35475\\n40772 49700\\n5447 42746\\n23497 29250\\n\", \"5\\n60522 167713\\n36426 133836\\n48772 148202\\n133447 125228\\n103497 63591\\n\", \"5\\n20522 4881\\n36426 45854\\n48772 33403\\n13447 20564\\n23497 16268\\n\", \"5\\n6522 1207\\n12426 6846\\n2772 4748\\n17447 20123\\n5497 2514\\n\", \"5\\n522 2785\\n16426 4821\\n8772 9458\\n13447 4313\\n3497 17838\\n\", \"5\\n522 3161\\n426 3209\\n772 2238\\n1447 1372\\n3497 3893\\n\", \"5\\n44522 55545\\n60426 6915\\n24772 6685\\n37447 10900\\n23497 34907\\n\", \"5\\n199991 200000\\n199992 200000\\n199992 200000\\n199992 200000\\n199996 200000\\n\", \"5\\n32522 22058\\n12426 18213\\n28772 45814\\n17447 46926\\n31497 1982\\n\", \"5\\n4522 7771\\n4426 15425\\n772 9303\\n13447 13626\\n15497 8407\\n\", \"5\\n2 200000\\n199991 200000\\n100000 1024\\n1024 0\\n200000 2048\\n\", \"5\\n20522 53736\\n56426 4658\\n16772 40371\\n73447 29991\\n23497 62948\\n\", \"5\\n12522 2866\\n20426 46782\\n24772 15392\\n45447 8381\\n31497 32520\\n\", \"5\\n22 578\\n26 604\\n72 839\\n47 857\\n97 400\\n\", \"5\\n80522 13536\\n6426 18454\\n78772 78078\\n73447 880\\n23497 82319\\n\", \"5\\n4522 2314\\n4426 2886\\n772 5081\\n5447 5120\\n7497 7239\\n\", \"5\\n200000 200000\\n200000 200000\\n200000 200000\\n200000 200000\\n200000 200000\\n\", \"5\\n36522 17830\\n16426 33675\\n32772 1463\\n37447 18818\\n39497 38127\\n\", \"5\\n20522 12967\\n36426 14501\\n8772 19546\\n13447 38726\\n23497 3234\\n\", \"5\\n20522 2314\\n4426 7311\\n16772 25205\\n13447 30239\\n15497 27795\\n\", \"5\\n10368 49291\\n36426 49737\\n48772 14993\\n33447 42227\\n3497 6588\\n\", \"5\\n26522 28224\\n6426 4535\\n24772 21028\\n53597 35982\\n17497 28737\\n\", \"5\\n40522 32643\\n6426 10515\\n38772 15930\\n3447 27180\\n3497 87432\\n\", \"5\\n20522 22180\\n6426 23733\\n18772 19072\\n13447 4385\\n23497 10041\\n\", \"5\\n20522 18334\\n12426 1766\\n772 12777\\n13447 20072\\n23497 22354\\n\", \"5\\n32522 70109\\n12426 71675\\n54772 11619\\n43447 28437\\n5497 59767\\n\", \"5\\n60522 34392\\n36426 92971\\n48772 47765\\n33447 90408\\n1977 41078\\n\", \"5\\n20522 9466\\n18426 17637\\n16772 16118\\n28836 22061\\n23497 36309\\n\", \"5\\n20522 53850\\n36426 24758\\n48772 85787\\n13447 69672\\n47497 92782\\n\", \"5\\n68522 77585\\n48426 29779\\n30653 57939\\n73447 34586\\n59497 1126\\n\", \"5\\n26522 80986\\n62426 38438\\n76772 37666\\n43447 27239\\n7745 10653\\n\", \"5\\n22 59\\n26 60\\n79 72\\n47 3\\n97 16\\n\", \"5\\n36522 6298\\n60426 75099\\n32772 49609\\n37447 40527\\n39497 68728\\n\", \"5\\n52522 10077\\n4426 42688\\n16772 108138\\n13447 55100\\n47497 39698\\n\", \"5\\n522 8443\\n8426 120\\n6772 3377\\n5447 9690\\n23497 31112\\n\", \"5\\n8522 3000\\n6702 17386\\n6772 11564\\n1447 9637\\n5497 16252\\n\", \"5\\n26522 46763\\n24426 20644\\n42772 46922\\n1447 50380\\n12509 32679\\n\", \"5\\n2522 4467\\n426 3791\\n772 1519\\n1447 2006\\n5497 2673\\n\", \"5\\n48522 65231\\n22426 125563\\n66772 58717\\n17447 24560\\n55497 76940\\n\", \"5\\n522 1278\\n6426 4981\\n8772 718\\n3447 3137\\n3497 8752\\n\", \"5\\n64522 50719\\n76426 17985\\n32772 22133\\n53447 62282\\n34986 50268\\n\", \"5\\n20522 15275\\n36426 23993\\n772 4851\\n13447 59754\\n47497 10125\\n\", \"5\\n8522 19723\\n24426 317\\n24772 34\\n1447 2271\\n23497 28632\\n\", \"5\\n14522 43036\\n60426 4985\\n54772 28204\\n37447 14445\\n17497 16728\\n\", \"5\\n46522 40903\\n2426 51978\\n6772 5583\\n43447 16967\\n9733 14176\\n\", \"5\\n60522 200000\\n36426 200000\\n48772 200000\\n133447 200000\\n103497 78892\\n\", \"5\\n737 1981\\n426 1890\\n772 1010\\n1447 1859\\n1497 1362\\n\", \"5\\n4522 31786\\n2426 2907\\n66772 47\\n5447 64736\\n47497 86552\\n\", \"5\\n200000 200000\\n24567 23423\\n1 200000\\n184952 1\\n200000 0\\n\", \"5\\n12522 19\\n1726 11199\\n10772 1658\\n3447 5303\\n3497 2454\\n\", \"5\\n28522 21694\\n40426 71172\\n52772 47783\\n61447 31928\\n27497 9127\\n\", \"5\\n18522 39204\\n30426 32870\\n35824 13018\\n7447 37823\\n5497 27005\\n\", \"5\\n22 167713\\n26 133836\\n72 148202\\n47 125228\\n69 63591\\n\", \"5\\n14522 5674\\n16426 10901\\n10772 1084\\n15447 20499\\n32857 3424\\n\", \"5\\n45710 72136\\n62426 69558\\n38772 16169\\n31447 52010\\n17497 84468\\n\", \"5\\n12522 27839\\n20426 1298\\n24772 26346\\n17447 22381\\n3497 17251\\n\", \"5\\n12522 3232\\n24426 29310\\n38772 5175\\n55447 18296\\n15497 9786\\n\", \"5\\n8522 11028\\n426 7666\\n772 2651\\n1447 9437\\n11497 840\\n\", \"5\\n20522 27100\\n36426 19806\\n48772 30101\\n13447 72881\\n84038 20955\\n\", \"5\\n522 35586\\n8426 35475\\n40772 49700\\n5447 42746\\n23497 29250\\n\", \"5\\n60522 167713\\n36426 133836\\n86045 148202\\n133447 125228\\n103497 63591\\n\", \"5\\n20522 4881\\n36426 40575\\n48772 33403\\n13447 20564\\n23497 16268\\n\", \"5\\n6522 1821\\n12426 6846\\n2772 4748\\n17447 20123\\n5497 2514\\n\", \"5\\n865 2785\\n16426 4821\\n8772 9458\\n13447 4313\\n3497 17838\\n\", \"5\\n522 6242\\n426 3209\\n772 2238\\n1447 1372\\n3497 3893\\n\", \"5\\n44522 55545\\n60426 6915\\n24772 6685\\n37447 10900\\n23497 12835\\n\", \"5\\n32522 22058\\n12426 18213\\n28772 45814\\n17447 43203\\n31497 1982\\n\", \"5\\n4522 7771\\n5605 15425\\n772 9303\\n13447 13626\\n15497 8407\\n\", \"5\\n31850 53736\\n56426 4658\\n16772 40371\\n73447 29991\\n23497 62948\\n\", \"5\\n12522 2866\\n20426 46782\\n48762 15392\\n45447 8381\\n31497 32520\\n\", \"5\\n22 578\\n26 604\\n72 839\\n47 857\\n177 400\\n\", \"5\\n80522 13536\\n6426 18454\\n78772 78078\\n73447 880\\n23497 62117\\n\", \"5\\n4522 2314\\n4449 2886\\n772 5081\\n5447 5120\\n7497 7239\\n\", \"5\\n36522 17830\\n16426 33675\\n32772 1463\\n37447 18818\\n63108 38127\\n\", \"5\\n20522 12967\\n36426 14501\\n8772 19546\\n13447 38726\\n23497 6055\\n\", \"5\\n20522 2314\\n4426 7311\\n1765 25205\\n13447 30239\\n15497 27795\\n\", \"3\\n6 1\\n2 1\\n4 0\\n\", \"5\\n10368 49291\\n36426 49737\\n48772 14993\\n26624 42227\\n3497 6588\\n\", \"5\\n26522 28224\\n6426 4535\\n24772 30934\\n53597 35982\\n17497 28737\\n\", \"5\\n40522 32643\\n6426 10515\\n38772 15930\\n3447 27180\\n3497 33600\\n\", \"5\\n20522 22180\\n6426 34893\\n18772 19072\\n13447 4385\\n23497 10041\\n\", \"5\\n20522 18334\\n12426 1766\\n772 12777\\n13447 19836\\n23497 22354\\n\", \"5\\n32522 70109\\n12426 71675\\n54772 11619\\n43447 28437\\n5497 53533\\n\", \"5\\n60522 34392\\n14088 92971\\n48772 47765\\n33447 90408\\n1977 41078\\n\", \"5\\n20522 9466\\n18426 31405\\n16772 16118\\n28836 22061\\n23497 36309\\n\", \"5\\n20522 53850\\n36426 24758\\n48772 85787\\n13447 69672\\n47497 23545\\n\", \"5\\n68522 77585\\n48426 29779\\n37068 57939\\n73447 34586\\n59497 1126\\n\", \"5\\n26522 80986\\n62426 38438\\n76772 37666\\n43447 27511\\n7745 10653\\n\", \"5\\n22 59\\n26 60\\n79 72\\n76 3\\n97 16\\n\", \"5\\n36522 6298\\n60426 75099\\n32772 49609\\n46921 40527\\n39497 68728\\n\", \"5\\n52522 10077\\n1865 42688\\n16772 108138\\n13447 55100\\n47497 39698\\n\", \"5\\n522 8443\\n8426 120\\n6772 3377\\n5447 9690\\n23497 37620\\n\", \"5\\n8522 3000\\n6702 17296\\n6772 11564\\n1447 9637\\n5497 16252\\n\", \"5\\n26522 46763\\n24426 20644\\n42772 46922\\n2411 50380\\n12509 32679\\n\", \"5\\n2522 4467\\n426 1266\\n772 1519\\n1447 2006\\n5497 2673\\n\", \"5\\n48522 65231\\n22426 125563\\n66772 58717\\n17447 41756\\n55497 76940\\n\", \"5\\n107 1278\\n6426 4981\\n8772 718\\n3447 3137\\n3497 8752\\n\", \"5\\n64522 50719\\n76426 17985\\n32772 22133\\n9301 62282\\n34986 50268\\n\", \"5\\n20522 15275\\n36426 23993\\n772 4851\\n13447 59754\\n47497 20012\\n\", \"5\\n8522 19723\\n21761 317\\n24772 34\\n1447 2271\\n23497 28632\\n\", \"5\\n14522 43036\\n60426 4985\\n54772 14533\\n37447 14445\\n17497 16728\\n\", \"5\\n46522 40903\\n2426 51978\\n6772 5583\\n43447 16967\\n9733 12200\\n\", \"5\\n27080 200000\\n36426 200000\\n48772 200000\\n133447 200000\\n103497 78892\\n\", \"5\\n737 1981\\n426 1890\\n772 1010\\n1447 1859\\n316 1362\\n\", \"5\\n4522 31786\\n2426 2907\\n66772 5\\n5447 64736\\n47497 86552\\n\", \"5\\n200000 200000\\n19782 23423\\n1 200000\\n184952 1\\n200000 0\\n\", \"5\\n12522 19\\n1726 11199\\n10772 1658\\n3447 5934\\n3497 2454\\n\", \"5\\n28522 21694\\n40426 71172\\n52772 47783\\n61447 31928\\n39524 9127\\n\", \"5\\n18522 41373\\n30426 32870\\n35824 13018\\n7447 37823\\n5497 27005\\n\", \"5\\n22 167713\\n26 133836\\n50 148202\\n47 125228\\n69 63591\\n\", \"5\\n14522 5674\\n16426 10901\\n10772 1084\\n15447 20499\\n56303 3424\\n\", \"5\\n45710 72136\\n62426 69558\\n38772 16169\\n57181 52010\\n17497 84468\\n\", \"5\\n12522 27839\\n20426 1298\\n24772 26346\\n4970 22381\\n3497 17251\\n\", \"5\\n12522 3232\\n25390 29310\\n38772 5175\\n55447 18296\\n15497 9786\\n\", \"5\\n8522 12811\\n426 7666\\n772 2651\\n1447 9437\\n11497 840\\n\", \"5\\n20522 27100\\n36426 19806\\n48772 30101\\n13447 72881\\n84038 1108\\n\", \"5\\n522 35586\\n8426 35475\\n40772 49700\\n5447 42746\\n24579 29250\\n\", \"5\\n60522 167713\\n4179 133836\\n86045 148202\\n133447 125228\\n103497 63591\\n\", \"5\\n20522 9712\\n36426 40575\\n48772 33403\\n13447 20564\\n23497 16268\\n\", \"5\\n6522 381\\n12426 6846\\n2772 4748\\n17447 20123\\n5497 2514\\n\", \"5\\n865 2785\\n16426 4821\\n8772 9458\\n13447 5763\\n3497 17838\\n\", \"5\\n522 6242\\n426 3209\\n772 1049\\n1447 1372\\n3497 3893\\n\", \"5\\n44522 55545\\n60426 6915\\n24772 6685\\n48366 10900\\n23497 12835\\n\", \"5\\n32522 22058\\n12426 15154\\n28772 45814\\n17447 43203\\n31497 1982\\n\", \"5\\n4522 7771\\n5605 15425\\n772 9303\\n13447 13626\\n15497 16168\\n\", \"5\\n31850 53736\\n56426 4658\\n5217 40371\\n73447 29991\\n23497 62948\\n\", \"5\\n12522 2866\\n20426 46782\\n48762 15392\\n45447 1390\\n31497 32520\\n\", \"5\\n22 578\\n26 203\\n72 839\\n47 857\\n177 400\\n\", \"5\\n80522 13536\\n6426 18454\\n78772 78078\\n73447 880\\n7820 62117\\n\", \"5\\n4522 2314\\n4449 2886\\n772 5081\\n9158 5120\\n7497 7239\\n\", \"5\\n36522 17830\\n16426 33675\\n32772 1463\\n37447 18818\\n114036 38127\\n\", \"5\\n20522 12967\\n36426 14501\\n8772 19546\\n13447 38726\\n23497 9095\\n\", \"5\\n20522 2314\\n7083 7311\\n1765 25205\\n13447 30239\\n15497 27795\\n\", \"3\\n6 1\\n2 0\\n4 0\\n\", \"5\\n10368 49291\\n36426 49737\\n48772 14993\\n26624 42227\\n3497 5469\\n\", \"5\\n26522 28224\\n6426 4535\\n24772 30934\\n53597 43861\\n17497 28737\\n\", \"5\\n40522 32643\\n6426 10515\\n38772 15930\\n3447 27180\\n5126 33600\\n\", \"5\\n20522 22180\\n6426 34893\\n18772 19072\\n22778 4385\\n23497 10041\\n\", \"5\\n20522 18334\\n12426 1766\\n772 12777\\n13447 34027\\n23497 22354\\n\", \"5\\n32522 70109\\n20082 71675\\n54772 11619\\n43447 28437\\n5497 53533\\n\", \"5\\n60522 34392\\n14088 165955\\n48772 47765\\n33447 90408\\n1977 41078\\n\", \"5\\n20522 9466\\n18426 31405\\n16772 30325\\n28836 22061\\n23497 36309\\n\", \"5\\n20522 53850\\n40776 24758\\n48772 85787\\n13447 69672\\n47497 23545\\n\", \"5\\n68522 77585\\n48426 29779\\n37068 57939\\n41419 34586\\n59497 1126\\n\", \"5\\n26522 80986\\n62426 38438\\n76772 37666\\n43447 27511\\n7745 20058\\n\", \"5\\n22 59\\n26 43\\n79 72\\n76 3\\n97 16\\n\", \"5\\n36522 6298\\n60426 75099\\n32772 49609\\n24009 40527\\n39497 68728\\n\", \"5\\n52522 10077\\n3443 42688\\n16772 108138\\n13447 55100\\n47497 39698\\n\", \"5\\n522 16871\\n8426 120\\n6772 3377\\n5447 9690\\n23497 37620\\n\", \"5\\n8522 3000\\n6702 17296\\n6772 321\\n1447 9637\\n5497 16252\\n\", \"5\\n29045 46763\\n24426 20644\\n42772 46922\\n2411 50380\\n12509 32679\\n\", \"5\\n2522 4467\\n426 1266\\n772 1519\\n972 2006\\n5497 2673\\n\", \"5\\n48522 65231\\n22426 125563\\n110708 58717\\n17447 41756\\n55497 76940\\n\", \"5\\n107 1278\\n6426 4981\\n8772 718\\n3447 2681\\n3497 8752\\n\", \"5\\n64522 50719\\n76426 17985\\n32772 22133\\n9301 32614\\n34986 50268\\n\", \"5\\n4123 15275\\n36426 23993\\n772 4851\\n13447 59754\\n47497 20012\\n\", \"5\\n8522 19723\\n21761 317\\n24772 34\\n1447 2271\\n23497 9156\\n\", \"5\\n14522 73218\\n60426 4985\\n54772 14533\\n37447 14445\\n17497 16728\\n\", \"5\\n46522 40903\\n2426 51978\\n6772 4387\\n43447 16967\\n9733 12200\\n\", \"5\\n27080 200000\\n36426 200000\\n88734 200000\\n133447 200000\\n103497 78892\\n\", \"5\\n737 1981\\n306 1890\\n772 1010\\n1447 1859\\n316 1362\\n\", \"5\\n4522 37761\\n2426 2907\\n66772 5\\n5447 64736\\n47497 86552\\n\", \"5\\n200000 200000\\n19782 16610\\n1 200000\\n184952 1\\n200000 0\\n\", \"5\\n12522 19\\n1726 11199\\n10772 1658\\n3447 8193\\n3497 2454\\n\", \"5\\n28522 21694\\n40426 71172\\n52772 47783\\n61447 41291\\n39524 9127\\n\", \"5\\n18522 41373\\n30426 33815\\n35824 13018\\n7447 37823\\n5497 27005\\n\", \"5\\n22 167713\\n1 133836\\n50 148202\\n47 125228\\n69 63591\\n\", \"5\\n14522 5674\\n16426 10901\\n10772 1084\\n15447 20499\\n56303 6606\\n\", \"5\\n45710 72136\\n62426 69558\\n38772 16169\\n57181 52010\\n9433 84468\\n\", \"5\\n12522 27839\\n20426 1298\\n24772 26346\\n3276 22381\\n3497 17251\\n\", \"5\\n12522 3232\\n25390 29310\\n38772 5175\\n55447 18296\\n12296 9786\\n\", \"5\\n8522 12811\\n426 7666\\n772 2651\\n1447 9437\\n4533 840\\n\", \"5\\n20522 27100\\n36426 19806\\n11881 30101\\n13447 72881\\n84038 1108\\n\", \"5\\n522 35586\\n8426 35475\\n40772 49700\\n5447 42746\\n24579 33460\\n\", \"5\\n23718 167713\\n4179 133836\\n86045 148202\\n133447 125228\\n103497 63591\\n\", \"5\\n20522 9712\\n36426 40575\\n48772 33403\\n13447 32718\\n23497 16268\\n\", \"5\\n6522 381\\n12426 6846\\n2772 4748\\n17447 34032\\n5497 2514\\n\", \"5\\n865 2785\\n16426 4821\\n8772 9458\\n13447 1230\\n3497 17838\\n\", \"5\\n121 6242\\n426 3209\\n772 1049\\n1447 1372\\n3497 3893\\n\", \"5\\n44522 55545\\n60426 7247\\n24772 6685\\n48366 10900\\n23497 12835\\n\", \"5\\n32522 22058\\n12426 15154\\n28772 45814\\n17447 76181\\n31497 1982\\n\", \"5\\n8811 7771\\n5605 15425\\n772 9303\\n13447 13626\\n15497 16168\\n\", \"5\\n31850 21804\\n56426 4658\\n5217 40371\\n73447 29991\\n23497 62948\\n\", \"5\\n12522 2866\\n20426 46782\\n48762 15392\\n45447 1390\\n31497 57025\\n\", \"5\\n22 578\\n26 316\\n72 839\\n47 857\\n177 400\\n\", \"5\\n80522 13536\\n6426 18454\\n78772 78078\\n73447 1613\\n7820 62117\\n\", \"5\\n4522 2314\\n4449 2886\\n772 2773\\n9158 5120\\n7497 7239\\n\", \"5\\n36522 17830\\n16426 33675\\n24974 1463\\n37447 18818\\n114036 38127\\n\", \"5\\n20522 3245\\n36426 14501\\n8772 19546\\n13447 38726\\n23497 9095\\n\", \"5\\n20522 2314\\n7083 7311\\n1765 6421\\n13447 30239\\n15497 27795\\n\", \"3\\n11 1\\n2 0\\n4 0\\n\", \"5\\n10368 18873\\n36426 49737\\n48772 14993\\n26624 42227\\n3497 5469\\n\", \"5\\n26522 28224\\n6426 4535\\n24772 30934\\n53597 43861\\n17497 10385\\n\", \"5\\n40522 32643\\n6426 10515\\n59150 15930\\n3447 27180\\n5126 33600\\n\", \"5\\n17044 22180\\n6426 34893\\n18772 19072\\n22778 4385\\n23497 10041\\n\", \"5\\n36416 18334\\n12426 1766\\n772 12777\\n13447 34027\\n23497 22354\\n\", \"5\\n32522 70109\\n20082 71675\\n54772 11619\\n43447 28437\\n5497 98083\\n\", \"5\\n60522 34392\\n14088 165955\\n46278 47765\\n33447 90408\\n1977 41078\\n\", \"5\\n20522 9466\\n36350 31405\\n16772 30325\\n28836 22061\\n23497 36309\\n\", \"5\\n20522 53850\\n40776 15824\\n48772 85787\\n13447 69672\\n47497 23545\\n\", \"5\\n68522 77585\\n48426 29779\\n37068 57939\\n41419 14040\\n59497 1126\\n\", \"5\\n26522 80986\\n62426 38438\\n76772 37666\\n43447 31510\\n7745 20058\\n\", \"5\\n39 59\\n26 43\\n79 72\\n76 3\\n97 16\\n\", \"5\\n36522 6298\\n60426 50487\\n32772 49609\\n24009 40527\\n39497 68728\\n\", \"5\\n522 16871\\n8426 120\\n12587 3377\\n5447 9690\\n23497 37620\\n\", \"5\\n4332 3000\\n6702 17296\\n6772 321\\n1447 9637\\n5497 16252\\n\", \"5\\n29045 46763\\n24426 20644\\n42772 46922\\n2411 50380\\n12509 35342\\n\", \"5\\n2522 4467\\n426 1242\\n772 1519\\n972 2006\\n5497 2673\\n\", \"5\\n48522 65231\\n22426 125563\\n110708 58717\\n17447 41756\\n55497 103847\\n\", \"5\\n182 1278\\n6426 4981\\n8772 718\\n3447 2681\\n3497 8752\\n\", \"5\\n64522 50719\\n76426 17985\\n32772 22133\\n9301 32614\\n56175 50268\\n\", \"5\\n4123 15275\\n36426 23993\\n772 4851\\n13431 59754\\n47497 20012\\n\", \"5\\n8522 19723\\n21761 317\\n24772 68\\n1447 2271\\n23497 9156\\n\", \"5\\n14522 73218\\n60426 1344\\n54772 14533\\n37447 14445\\n17497 16728\\n\", \"5\\n46522 76663\\n2426 51978\\n6772 4387\\n43447 16967\\n9733 12200\\n\", \"5\\n27080 200000\\n20670 200000\\n88734 200000\\n133447 200000\\n103497 78892\\n\", \"5\\n737 1981\\n286 1890\\n772 1010\\n1447 1859\\n316 1362\\n\", \"5\\n4522 37761\\n2426 2907\\n66772 5\\n5447 64736\\n9712 86552\\n\", \"5\\n200000 123277\\n19782 16610\\n1 200000\\n184952 1\\n200000 0\\n\", \"5\\n12522 19\\n1726 11199\\n10772 2036\\n3447 8193\\n3497 2454\\n\", \"3\\n3 1\\n2 1\\n4 0\\n\"], \"outputs\": [\"5\\n2\\n1\\n\", \"226490044\\n470587519\\n175895282\\n87947641\\n1\\n\", \"4428492\\n573667126\\n741012999\\n1\\n386630993\\n\", \"573667126\\n913020909\\n913020909\\n913020909\\n41788052\\n\", \"226490044\\n226490044\\n226490044\\n226490044\\n226490044\\n\", \"418576030\\n232137381\\n395057418\\n5669223\\n765611330\\n\", \"88692754\\n877803650\\n810867890\\n817679867\\n55853432\\n\", \"304668051\\n8504791\\n826876273\\n876327971\\n867434228\\n\", \"719147166\\n712743436\\n592556526\\n300790496\\n472187775\\n\", \"31027543\\n136918279\\n784949490\\n553888953\\n423365820\\n\", \"128766123\\n527181212\\n212725943\\n540481455\\n161044419\\n\", \"270381413\\n22435266\\n915213608\\n465693385\\n486274412\\n\", \"387599759\\n635311356\\n552472895\\n752772609\\n931791909\\n\", \"583234568\\n559552720\\n122646970\\n48480085\\n917539288\\n\", \"501733812\\n294571525\\n722429686\\n914702675\\n280411108\\n\", \"513847\\n273162268\\n889133064\\n851232032\\n371101041\\n\", \"525725396\\n826606325\\n692029170\\n486489284\\n495668637\\n\", \"814565803\\n486206530\\n368488320\\n3354994\\n899076399\\n\", \"389346184\\n345023944\\n936288148\\n96774688\\n697294112\\n\", \"440235472\\n659823308\\n469802878\\n46158886\\n333866633\\n\", \"992009897\\n858050302\\n314846315\\n338328822\\n241087122\\n\", \"258002497\\n24400553\\n383535095\\n564262189\\n141733393\\n\", \"222061841\\n456839279\\n641365823\\n295160810\\n605774697\\n\", \"627048439\\n692531689\\n257860359\\n672149186\\n484947029\\n\", \"373779991\\n752041429\\n675278712\\n56027611\\n995446610\\n\", \"387713371\\n567907291\\n567266418\\n203396676\\n877257118\\n\", \"643620372\\n188787712\\n137493209\\n985755740\\n63055698\\n\", \"383106358\\n628462794\\n993108917\\n908084822\\n666947024\\n\", \"311763651\\n947379706\\n930924417\\n51525703\\n485235024\\n\", \"250838410\\n728681630\\n204085208\\n354081072\\n252539854\\n\", \"614165725\\n295215954\\n111774336\\n788811583\\n94457069\\n\", \"577845706\\n434136514\\n327930500\\n445732548\\n64901596\\n\", \"574158496\\n375944045\\n191068937\\n374319462\\n675339196\\n\", \"92383711\\n556307867\\n214845295\\n536176885\\n274345529\\n\", \"357088684\\n352090898\\n955599131\\n643643684\\n112221458\\n\", \"941012026\\n735826088\\n313320819\\n406320729\\n449754690\\n\", \"420121807\\n910007568\\n314559436\\n499243470\\n664092465\\n\", \"59985038\\n334121\\n139590791\\n847779639\\n571037452\\n\", \"967627092\\n37949128\\n600680035\\n666312473\\n626901798\\n\", \"229899021\\n477092059\\n917047148\\n793264543\\n794742767\\n\", \"696066472\\n793085020\\n101346244\\n47764496\\n12580539\\n\", \"809810100\\n223467262\\n929221981\\n920037472\\n559355407\\n\", \"819216143\\n42480091\\n344412023\\n800016372\\n228614960\\n\", \"74659798\\n451164750\\n71292169\\n55083431\\n893651755\\n\", \"964909104\\n163185257\\n287214352\\n745808150\\n311967807\\n\", \"174955742\\n88129650\\n238023853\\n148013756\\n539202850\\n\", \"243258496\\n546453886\\n657584641\\n295422815\\n581001485\\n\", \"800737564\\n983143562\\n489457079\\n594790725\\n702380134\\n\", \"259396182\\n765449308\\n27678822\\n989349622\\n136295276\\n\", \"845118508\\n102134845\\n740378448\\n957821706\\n759188985\\n\", \"15029095\\n525260305\\n861843978\\n164167061\\n701313289\\n\", \"618495042\\n550975242\\n522053296\\n783499166\\n960428842\\n\", \"518077479\\n596707440\\n638440559\\n973868480\\n799215443\\n\", \"260751469\\n836872195\\n12494412\\n153815728\\n709694981\\n\", \"812348970\\n719313504\\n248545775\\n654529015\\n5930487\\n\", \"704169853\\n729060138\\n881606279\\n991848271\\n544274182\\n\", \"936486310\\n24729470\\n774762575\\n257895456\\n323271573\\n\", \"3597531\\n233500310\\n975586073\\n89817081\\n124854905\\n\", \"991039517\\n66825943\\n357651709\\n703220994\\n505948904\\n\", \"991485105\\n482392881\\n132303178\\n849810533\\n55123956\\n\", \"1\\n\", \"357088684\\n352090898\\n955599131\\n643643684\\n112221458\\n\", \"614165725\\n295215954\\n111774336\\n788811583\\n94457069\\n\", \"964909104\\n163185257\\n287214352\\n745808150\\n311967807\\n\", \"373779991\\n752041429\\n675278712\\n56027611\\n995446610\\n\", \"258002497\\n24400553\\n383535095\\n564262189\\n141733393\\n\", \"259396182\\n765449308\\n27678822\\n989349622\\n136295276\\n\", \"991485105\\n482392881\\n132303178\\n849810533\\n55123956\\n\", \"311763651\\n947379706\\n930924417\\n51525703\\n485235024\\n\", \"3597531\\n233500310\\n975586073\\n89817081\\n124854905\\n\", \"618495042\\n550975242\\n522053296\\n783499166\\n960428842\\n\", \"15029095\\n525260305\\n861843978\\n164167061\\n701313289\\n\", \"719147166\\n712743436\\n592556526\\n300790496\\n472187775\\n\", \"260751469\\n836872195\\n12494412\\n153815728\\n709694981\\n\", \"809810100\\n223467262\\n929221981\\n920037472\\n559355407\\n\", \"643620372\\n188787712\\n137493209\\n985755740\\n63055698\\n\", \"389346184\\n345023944\\n936288148\\n96774688\\n697294112\\n\", \"420121807\\n910007568\\n314559436\\n499243470\\n664092465\\n\", \"387599759\\n635311356\\n552472895\\n752772609\\n931791909\\n\", \"936486310\\n24729470\\n774762575\\n257895456\\n323271573\\n\", \"501733812\\n294571525\\n722429686\\n914702675\\n280411108\\n\", \"704169853\\n729060138\\n881606279\\n991848271\\n544274182\\n\", \"92383711\\n556307867\\n214845295\\n536176885\\n274345529\\n\", \"383106358\\n628462794\\n993108917\\n908084822\\n666947024\\n\", \"819216143\\n42480091\\n344412023\\n800016372\\n228614960\\n\", \"967627092\\n37949128\\n600680035\\n666312473\\n626901798\\n\", \"88692754\\n877803650\\n810867890\\n817679867\\n55853432\\n\", \"128766123\\n527181212\\n212725943\\n540481455\\n161044419\\n\", \"243258496\\n546453886\\n657584641\\n295422815\\n581001485\\n\", \"226490044\\n470587519\\n175895282\\n87947641\\n1\\n\", \"525725396\\n826606325\\n692029170\\n486489284\\n495668637\\n\", \"518077479\\n596707440\\n638440559\\n973868480\\n799215443\\n\", \"574158496\\n375944045\\n191068937\\n374319462\\n675339196\\n\", \"304668051\\n8504791\\n826876273\\n876327971\\n867434228\\n\", \"992009897\\n858050302\\n314846315\\n338328822\\n241087122\\n\", \"991039517\\n66825943\\n357651709\\n703220994\\n505948904\\n\", \"1\\n\", \"627048439\\n692531689\\n257860359\\n672149186\\n484947029\\n\", \"696066472\\n793085020\\n101346244\\n47764496\\n12580539\\n\", \"513847\\n273162268\\n889133064\\n851232032\\n371101041\\n\", \"845118508\\n102134845\\n740378448\\n957821706\\n759188985\\n\", \"74659798\\n451164750\\n71292169\\n55083431\\n893651755\\n\", \"418576030\\n232137381\\n395057418\\n5669223\\n765611330\\n\", \"229899021\\n477092059\\n917047148\\n793264543\\n794742767\\n\", \"222061841\\n456839279\\n641365823\\n295160810\\n605774697\\n\", \"440235472\\n659823308\\n469802878\\n46158886\\n333866633\\n\", \"270381413\\n22435266\\n915213608\\n465693385\\n486274412\\n\", \"174955742\\n88129650\\n238023853\\n148013756\\n539202850\\n\", \"573667126\\n913020909\\n913020909\\n913020909\\n41788052\\n\", \"941012026\\n735826088\\n313320819\\n406320729\\n449754690\\n\", \"814565803\\n486206530\\n368488320\\n3354994\\n899076399\\n\", \"4428492\\n573667126\\n741012999\\n1\\n386630993\\n\", \"800737564\\n983143562\\n489457079\\n594790725\\n702380134\\n\", \"59985038\\n334121\\n139590791\\n847779639\\n571037452\\n\", \"31027543\\n136918279\\n784949490\\n553888953\\n423365820\\n\", \"812348970\\n719313504\\n248545775\\n654529015\\n5930487\\n\", \"583234568\\n559552720\\n122646970\\n48480085\\n917539288\\n\", \"226490044\\n226490044\\n226490044\\n226490044\\n226490044\\n\", \"577845706\\n434136514\\n327930500\\n445732548\\n64901596\\n\", \"250838410\\n728681630\\n204085208\\n354081072\\n252539854\\n\", \"387713371\\n567907291\\n567266418\\n203396676\\n877257118\\n\", \"962519939\\n352090898\\n955599131\\n643643684\\n112221458\\n\", \"614165725\\n295215954\\n111774336\\n548395046\\n94457069\\n\", \"964909104\\n163185257\\n287214352\\n745808150\\n422886835\\n\", \"843604177\\n752041429\\n675278712\\n56027611\\n995446610\\n\", \"84418281\\n24400553\\n383535095\\n564262189\\n141733393\\n\", \"259396182\\n765449308\\n27678822\\n475160540\\n136295276\\n\", \"991485105\\n482392881\\n132303178\\n849810533\\n515606795\\n\", \"311763651\\n947379706\\n930924417\\n434744855\\n485235024\\n\", \"3597531\\n988611239\\n975586073\\n89817081\\n124854905\\n\", \"618495042\\n550975242\\n658781405\\n783499166\\n960428842\\n\", \"15029095\\n525260305\\n861843978\\n164167061\\n722916729\\n\", \"719147166\\n712743436\\n465791863\\n300790496\\n472187775\\n\", \"260751469\\n712135690\\n12494412\\n153815728\\n709694981\\n\", \"809810100\\n223467262\\n366557486\\n920037472\\n559355407\\n\", \"643620372\\n188787712\\n156698449\\n985755740\\n63055698\\n\", \"389346184\\n169580882\\n936288148\\n96774688\\n697294112\\n\", \"420121807\\n910007568\\n314559436\\n499243470\\n269022892\\n\", \"387599759\\n635311356\\n583820765\\n752772609\\n931791909\\n\", \"936486310\\n969932624\\n774762575\\n257895456\\n323271573\\n\", \"501733812\\n294571525\\n310829741\\n914702675\\n280411108\\n\", \"704169853\\n729060138\\n881606279\\n991848271\\n578744329\\n\", \"92383711\\n556307867\\n214845295\\n335360331\\n274345529\\n\", \"383106358\\n628462794\\n993108917\\n908084822\\n575141644\\n\", \"819216143\\n42480091\\n344412023\\n85494388\\n228614960\\n\", \"967627092\\n37949128\\n600680035\\n666312473\\n885941179\\n\", \"88692754\\n877803650\\n810867890\\n817679867\\n361071905\\n\", \"659183945\\n527181212\\n212725943\\n540481455\\n161044419\\n\", \"243258496\\n546453886\\n657584641\\n295422815\\n216327584\\n\", \"226490044\\n470587519\\n175895282\\n576054208\\n1\\n\", \"525725396\\n203476650\\n692029170\\n486489284\\n495668637\\n\", \"518077479\\n596707440\\n638440559\\n973868480\\n6241081\\n\", \"574158496\\n375944045\\n916672881\\n374319462\\n675339196\\n\", \"304668051\\n8504791\\n826876273\\n876327971\\n324620302\\n\", \"992009897\\n858050302\\n314846315\\n338328822\\n787155175\\n\", \"667900504\\n66825943\\n357651709\\n703220994\\n505948904\\n\", \"627048439\\n207289780\\n257860359\\n672149186\\n484947029\\n\", \"696066472\\n793085020\\n381400197\\n47764496\\n12580539\\n\", \"513847\\n273162268\\n553311777\\n851232032\\n371101041\\n\", \"845118508\\n102134845\\n740378448\\n957821706\\n435195756\\n\", \"264326675\\n451164750\\n71292169\\n55083431\\n893651755\\n\", \"418576030\\n232137381\\n676216440\\n5669223\\n765611330\\n\", \"229899021\\n205656744\\n917047148\\n793264543\\n794742767\\n\", \"816980437\\n456839279\\n641365823\\n295160810\\n605774697\\n\", \"430750420\\n659823308\\n469802878\\n46158886\\n333866633\\n\", \"624112505\\n22435266\\n915213608\\n465693385\\n486274412\\n\", \"174955742\\n88129650\\n238023853\\n148013756\\n365269213\\n\", \"941012026\\n735826088\\n313320819\\n3034297\\n449754690\\n\", \"814565803\\n263786832\\n368488320\\n3354994\\n899076399\\n\", \"618413483\\n983143562\\n489457079\\n594790725\\n702380134\\n\", \"59985038\\n334121\\n770561942\\n847779639\\n571037452\\n\", \"31027543\\n136918279\\n784949490\\n553888953\\n674573905\\n\", \"812348970\\n719313504\\n248545775\\n654529015\\n466200220\\n\", \"583234568\\n379201756\\n122646970\\n48480085\\n917539288\\n\", \"577845706\\n434136514\\n327930500\\n445732548\\n355226183\\n\", \"250838410\\n728681630\\n204085208\\n354081072\\n301303785\\n\", \"387713371\\n567907291\\n169751889\\n203396676\\n877257118\\n\", \"32\\n2\\n1\\n\", \"962519939\\n352090898\\n955599131\\n720530893\\n112221458\\n\", \"614165725\\n295215954\\n652862586\\n548395046\\n94457069\\n\", \"964909104\\n163185257\\n287214352\\n745808150\\n806639655\\n\", \"843604177\\n374949698\\n675278712\\n56027611\\n995446610\\n\", \"84418281\\n24400553\\n383535095\\n345940935\\n141733393\\n\", \"259396182\\n765449308\\n27678822\\n475160540\\n323672158\\n\", \"991485105\\n343080265\\n132303178\\n849810533\\n515606795\\n\", \"311763651\\n883093407\\n930924417\\n434744855\\n485235024\\n\", \"3597531\\n988611239\\n975586073\\n89817081\\n411836263\\n\", \"618495042\\n550975242\\n878068245\\n783499166\\n960428842\\n\", \"15029095\\n525260305\\n861843978\\n843200081\\n722916729\\n\", \"719147166\\n712743436\\n465791863\\n27289574\\n472187775\\n\", \"260751469\\n712135690\\n12494412\\n103120306\\n709694981\\n\", \"809810100\\n681108238\\n366557486\\n920037472\\n559355407\\n\", \"643620372\\n188787712\\n156698449\\n985755740\\n750830809\\n\", \"389346184\\n390067143\\n936288148\\n96774688\\n697294112\\n\", \"420121807\\n910007568\\n314559436\\n315340067\\n269022892\\n\", \"387599759\\n635025671\\n583820765\\n752772609\\n931791909\\n\", \"936486310\\n969932624\\n774762575\\n957183965\\n323271573\\n\", \"932478654\\n294571525\\n310829741\\n914702675\\n280411108\\n\", \"704169853\\n729060138\\n881606279\\n528131859\\n578744329\\n\", \"92383711\\n556307867\\n214845295\\n335360331\\n652805338\\n\", \"383106358\\n457707572\\n993108917\\n908084822\\n575141644\\n\", \"819216143\\n42480091\\n77519662\\n85494388\\n228614960\\n\", \"967627092\\n37949128\\n600680035\\n666312473\\n566628432\\n\", \"354580771\\n877803650\\n810867890\\n817679867\\n361071905\\n\", \"659183945\\n527181212\\n212725943\\n540481455\\n839739738\\n\", \"243258496\\n546453886\\n762804059\\n295422815\\n216327584\\n\", \"226490044\\n590440006\\n175895282\\n576054208\\n1\\n\", \"525725396\\n203476650\\n692029170\\n522870460\\n495668637\\n\", \"518077479\\n596707440\\n638440559\\n973868480\\n192786667\\n\", \"415001464\\n375944045\\n916672881\\n374319462\\n675339196\\n\", \"304668051\\n8504791\\n514187665\\n876327971\\n324620302\\n\", \"992009897\\n858050302\\n314846315\\n338328822\\n439624004\\n\", \"667900504\\n66825943\\n357651709\\n200620862\\n505948904\\n\", \"627048439\\n207289780\\n257860359\\n943997152\\n484947029\\n\", \"696066472\\n425743690\\n381400197\\n47764496\\n12580539\\n\", \"439196343\\n273162268\\n553311777\\n851232032\\n371101041\\n\", \"845118508\\n102134845\\n740378448\\n957821706\\n143037953\\n\", \"264326675\\n451164750\\n71292169\\n55083431\\n725128449\\n\", \"418576030\\n966230899\\n676216440\\n5669223\\n765611330\\n\", \"30999455\\n205656744\\n917047148\\n793264543\\n794742767\\n\", \"249206783\\n456839279\\n641365823\\n295160810\\n605774697\\n\", \"430750420\\n659823308\\n469802878\\n429850710\\n333866633\\n\", \"624112505\\n22435266\\n144141158\\n465693385\\n486274412\\n\", \"174955742\\n88129650\\n238023853\\n767802751\\n365269213\\n\", \"941012026\\n323485130\\n313320819\\n3034297\\n449754690\\n\", \"814565803\\n263786832\\n368488320\\n3354994\\n467927453\\n\", \"618413483\\n983143562\\n116464894\\n594790725\\n702380134\\n\", \"59985038\\n334121\\n770561942\\n295577166\\n571037452\\n\", \"31027543\\n235861555\\n784949490\\n553888953\\n674573905\\n\", \"812348970\\n719313504\\n248545775\\n654529015\\n73728753\\n\", \"583234568\\n379201756\\n122646970\\n992779010\\n917539288\\n\", \"577845706\\n434136514\\n327930500\\n445732548\\n813578087\\n\", \"250838410\\n728681630\\n204085208\\n354081072\\n691372911\\n\", \"387713371\\n820001731\\n169751889\\n203396676\\n877257118\\n\", \"32\\n1\\n1\\n\", \"962519939\\n352090898\\n955599131\\n720530893\\n679469099\\n\", \"614165725\\n295215954\\n652862586\\n732463604\\n94457069\\n\", \"964909104\\n163185257\\n287214352\\n745808150\\n827844317\\n\", \"843604177\\n374949698\\n675278712\\n223013178\\n995446610\\n\", \"84418281\\n24400553\\n383535095\\n620476574\\n141733393\\n\", \"259396182\\n739631633\\n27678822\\n475160540\\n323672158\\n\", \"991485105\\n117741821\\n132303178\\n849810533\\n515606795\\n\", \"311763651\\n883093407\\n883590317\\n434744855\\n485235024\\n\", \"3597531\\n626956516\\n975586073\\n89817081\\n411836263\\n\", \"618495042\\n550975242\\n878068245\\n31097867\\n960428842\\n\", \"15029095\\n525260305\\n861843978\\n843200081\\n479668196\\n\", \"719147166\\n759166884\\n465791863\\n27289574\\n472187775\\n\", \"260751469\\n712135690\\n12494412\\n413875199\\n709694981\\n\", \"809810100\\n893455267\\n366557486\\n920037472\\n559355407\\n\", \"33173077\\n188787712\\n156698449\\n985755740\\n750830809\\n\", \"389346184\\n390067143\\n570166281\\n96774688\\n697294112\\n\", \"402000702\\n910007568\\n314559436\\n315340067\\n269022892\\n\", \"387599759\\n635025671\\n583820765\\n645621117\\n931791909\\n\", \"936486310\\n969932624\\n66184061\\n957183965\\n323271573\\n\", \"932478654\\n294571525\\n310829741\\n900536321\\n280411108\\n\", \"704169853\\n729060138\\n881606279\\n176050154\\n578744329\\n\", \"125852900\\n556307867\\n214845295\\n335360331\\n652805338\\n\", \"383106358\\n457707572\\n993108917\\n908084822\\n262602760\\n\", \"780240633\\n42480091\\n77519662\\n85494388\\n228614960\\n\", \"967627092\\n37949128\\n322806260\\n666312473\\n566628432\\n\", \"354580771\\n877803650\\n109729035\\n817679867\\n361071905\\n\", \"659183945\\n702889497\\n212725943\\n540481455\\n839739738\\n\", \"849907481\\n546453886\\n762804059\\n295422815\\n216327584\\n\", \"226490044\\n733390771\\n175895282\\n576054208\\n1\\n\", \"525725396\\n203476650\\n692029170\\n495091604\\n495668637\\n\", \"518077479\\n596707440\\n638440559\\n888898409\\n192786667\\n\", \"415001464\\n215780429\\n916672881\\n374319462\\n675339196\\n\", \"304668051\\n643726300\\n514187665\\n876327971\\n324620302\\n\", \"992009897\\n858050302\\n314846315\\n338328822\\n859169016\\n\", \"667900504\\n66825943\\n357651709\\n200620862\\n931635169\\n\", \"627048439\\n207289780\\n257860359\\n134948499\\n484947029\\n\", \"696066472\\n425743690\\n381400197\\n47764496\\n801971437\\n\", \"439196343\\n273162268\\n553311777\\n851232032\\n961564829\\n\", \"845118508\\n102134845\\n308421711\\n957821706\\n143037953\\n\", \"264326675\\n451164750\\n71292169\\n55083431\\n926255880\\n\", \"200295862\\n966230899\\n676216440\\n5669223\\n765611330\\n\", \"30999455\\n205656744\\n917047148\\n910134552\\n794742767\\n\", \"249206783\\n456839279\\n641365823\\n267998238\\n605774697\\n\", \"430750420\\n659823308\\n469802878\\n409505146\\n333866633\\n\", \"219563830\\n22435266\\n144141158\\n465693385\\n486274412\\n\", \"174955742\\n618617105\\n238023853\\n767802751\\n365269213\\n\", \"941012026\\n323485130\\n313320819\\n312544445\\n449754690\\n\", \"61897272\\n263786832\\n368488320\\n3354994\\n467927453\\n\", \"651169113\\n983143562\\n116464894\\n594790725\\n702380134\\n\", \"59985038\\n334121\\n770561942\\n295577166\\n333277452\\n\", \"31027543\\n449620269\\n784949490\\n553888953\\n674573905\\n\", \"812348970\\n719313504\\n248545775\\n663680543\\n73728753\\n\", \"583234568\\n379201756\\n215924075\\n992779010\\n917539288\\n\", \"577845706\\n434136514\\n729412809\\n445732548\\n813578087\\n\", \"776910153\\n728681630\\n204085208\\n354081072\\n691372911\\n\", \"387713371\\n820001731\\n837042964\\n203396676\\n877257118\\n\", \"1025\\n1\\n1\\n\", \"642407172\\n352090898\\n955599131\\n720530893\\n679469099\\n\", \"614165725\\n295215954\\n652862586\\n732463604\\n724391587\\n\", \"964909104\\n163185257\\n87885121\\n745808150\\n827844317\\n\", \"402409330\\n374949698\\n675278712\\n223013178\\n995446610\\n\", \"955416096\\n24400553\\n383535095\\n620476574\\n141733393\\n\", \"259396182\\n739631633\\n27678822\\n475160540\\n172956203\\n\", \"991485105\\n117741821\\n46688961\\n849810533\\n515606795\\n\", \"311763651\\n538362821\\n883590317\\n434744855\\n485235024\\n\", \"3597531\\n612281034\\n975586073\\n89817081\\n411836263\\n\", \"618495042\\n550975242\\n878068245\\n481236227\\n960428842\\n\", \"15029095\\n525260305\\n861843978\\n171922684\\n479668196\\n\", \"983579342\\n759166884\\n465791863\\n27289574\\n472187775\\n\", \"260751469\\n867808244\\n12494412\\n413875199\\n709694981\\n\", \"33173077\\n188787712\\n811351276\\n985755740\\n750830809\\n\", \"884618132\\n390067143\\n570166281\\n96774688\\n697294112\\n\", \"402000702\\n910007568\\n314559436\\n315340067\\n935519964\\n\", \"387599759\\n656184174\\n583820765\\n645621117\\n931791909\\n\", \"936486310\\n969932624\\n66184061\\n957183965\\n578491542\\n\", \"245933601\\n294571525\\n310829741\\n900536321\\n280411108\\n\", \"704169853\\n729060138\\n881606279\\n176050154\\n343356380\\n\", \"125852900\\n556307867\\n214845295\\n5313405\\n652805338\\n\", \"383106358\\n457707572\\n753919688\\n908084822\\n262602760\\n\", \"780240633\\n258347426\\n77519662\\n85494388\\n228614960\\n\", \"482723877\\n37949128\\n322806260\\n666312473\\n566628432\\n\", \"354580771\\n781975774\\n109729035\\n817679867\\n361071905\\n\", \"659183945\\n880631845\\n212725943\\n540481455\\n839739738\\n\", \"849907481\\n546453886\\n762804059\\n295422815\\n81777252\\n\", \"70726467\\n733390771\\n175895282\\n576054208\\n1\\n\", \"525725396\\n203476650\\n391705876\\n495091604\\n495668637\\n\", \"5\\n2\\n1\\n\"]}", "source": "taco"}
|
Moamen and Ezzat are playing a game. They create an array $a$ of $n$ non-negative integers where every element is less than $2^k$.
Moamen wins if $a_1 \,\&\, a_2 \,\&\, a_3 \,\&\, \ldots \,\&\, a_n \ge a_1 \oplus a_2 \oplus a_3 \oplus \ldots \oplus a_n$.
Here $\&$ denotes the bitwise AND operation , and $\oplus$ denotes the bitwise XOR operation .
Please calculate the number of winning for Moamen arrays $a$.
As the result may be very large, print the value modulo $1000000\,007$ ($10^9 + 7$).
-----Input-----
The first line contains a single integer $t$ ($1 \le t \le 5$)— the number of test cases.
Each test case consists of one line containing two integers $n$ and $k$ ($1 \le n\le 2\cdot 10^5$, $0 \le k \le 2\cdot 10^5$).
-----Output-----
For each test case, print a single value — the number of different arrays that Moamen wins with.
Print the result modulo $1000000\,007$ ($10^9 + 7$).
-----Examples-----
Input
3
3 1
2 1
4 0
Output
5
2
1
-----Note-----
In the first example, $n = 3$, $k = 1$. As a result, all the possible arrays are $[0,0,0]$, $[0,0,1]$, $[0,1,0]$, $[1,0,0]$, $[1,1,0]$, $[0,1,1]$, $[1,0,1]$, and $[1,1,1]$.
Moamen wins in only $5$ of them: $[0,0,0]$, $[1,1,0]$, $[0,1,1]$, $[1,0,1]$, and $[1,1,1]$.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"5 2\\n50 110 130 40 120\\n\", \"4 1\\n2 3 4 1\\n\", \"1 1\\n4\\n\", \"2 2\\n7 5\\n\", \"3 2\\n34 3 75\\n\", \"5 2\\n932 328 886 96 589\\n\", \"10 4\\n810 8527 9736 3143 2341 6029 7474 707 2513 2023\\n\", \"20 11\\n924129 939902 178964 918687 720767 695035 577430 407131 213304 810868 596349 266075 123602 376312 36680 18426 716200 121546 61834 851586\\n\", \"100 28\\n1 2 3 5 1 1 1 4 1 5 2 4 3 2 5 4 1 1 4 1 4 5 4 1 4 5 1 3 5 1 1 1 4 2 5 2 3 5 2 2 3 2 4 5 5 5 5 1 2 4 1 3 1 1 1 4 3 1 5 2 5 1 3 3 2 4 5 1 1 3 4 1 1 3 3 1 2 4 3 3 4 4 3 1 2 1 5 1 4 4 2 3 1 3 3 4 2 4 1 1\\n\", \"101 9\\n3 2 2 1 4 1 3 2 3 4 3 2 3 1 4 4 1 1 4 1 3 3 4 1 2 1 1 3 1 2 2 4 3 1 4 3 1 1 4 4 1 2 1 1 4 2 3 4 1 2 1 4 4 1 4 3 1 4 2 1 2 1 4 3 4 3 4 2 2 4 3 2 1 3 4 3 2 2 4 3 3 2 4 1 3 2 2 4 1 3 4 2 1 3 3 2 2 1 1 3 1\\n\", \"2 2\\n1 1000000000\\n\", \"2 1\\n1 1000000000\\n\", \"11 3\\n412 3306 3390 2290 1534 316 1080 2860 253 230 3166\\n\", \"10 3\\n2414 294 184 666 2706 1999 2201 1270 904 653\\n\", \"24 4\\n33 27 12 65 19 6 46 33 57 2 21 50 73 13 59 69 51 45 39 1 6 64 39 27\\n\", \"24 4\\n33 27 12 65 19 6 46 33 57 2 21 50 73 13 59 69 51 45 39 1 6 64 39 27\\n\", \"10 4\\n810 8527 9736 3143 2341 6029 7474 707 2513 2023\\n\", \"11 3\\n412 3306 3390 2290 1534 316 1080 2860 253 230 3166\\n\", \"2 2\\n1 1000000000\\n\", \"1 1\\n4\\n\", \"101 9\\n3 2 2 1 4 1 3 2 3 4 3 2 3 1 4 4 1 1 4 1 3 3 4 1 2 1 1 3 1 2 2 4 3 1 4 3 1 1 4 4 1 2 1 1 4 2 3 4 1 2 1 4 4 1 4 3 1 4 2 1 2 1 4 3 4 3 4 2 2 4 3 2 1 3 4 3 2 2 4 3 3 2 4 1 3 2 2 4 1 3 4 2 1 3 3 2 2 1 1 3 1\\n\", \"10 3\\n2414 294 184 666 2706 1999 2201 1270 904 653\\n\", \"3 2\\n34 3 75\\n\", \"20 11\\n924129 939902 178964 918687 720767 695035 577430 407131 213304 810868 596349 266075 123602 376312 36680 18426 716200 121546 61834 851586\\n\", \"2 1\\n1 1000000000\\n\", \"5 2\\n932 328 886 96 589\\n\", \"2 2\\n7 5\\n\", \"100 28\\n1 2 3 5 1 1 1 4 1 5 2 4 3 2 5 4 1 1 4 1 4 5 4 1 4 5 1 3 5 1 1 1 4 2 5 2 3 5 2 2 3 2 4 5 5 5 5 1 2 4 1 3 1 1 1 4 3 1 5 2 5 1 3 3 2 4 5 1 1 3 4 1 1 3 3 1 2 4 3 3 4 4 3 1 2 1 5 1 4 4 2 3 1 3 3 4 2 4 1 1\\n\", \"24 4\\n33 27 12 65 19 6 46 33 57 4 21 50 73 13 59 69 51 45 39 1 6 64 39 27\\n\", \"10 4\\n810 8527 9736 3143 2341 6029 7474 707 2513 637\\n\", \"11 3\\n789 3306 3390 2290 1534 316 1080 2860 253 230 3166\\n\", \"2 2\\n2 1000000000\\n\", \"101 9\\n3 2 2 1 4 1 3 2 3 4 3 2 3 1 4 4 1 1 4 1 3 3 4 1 2 1 1 3 1 2 2 4 3 1 4 3 1 1 4 4 1 2 1 1 4 2 3 4 1 2 1 4 4 1 4 3 1 4 2 1 2 1 4 3 4 3 4 2 2 4 3 2 1 1 4 3 2 2 4 3 3 2 4 1 3 2 2 4 1 3 4 2 1 3 3 2 2 1 1 3 1\\n\", \"10 3\\n2414 445 184 666 2706 1999 2201 1270 904 653\\n\", \"20 20\\n924129 939902 178964 918687 720767 695035 577430 407131 213304 810868 596349 266075 123602 376312 36680 18426 716200 121546 61834 851586\\n\", \"5 2\\n932 328 173 96 589\\n\", \"2 2\\n12 5\\n\", \"100 28\\n1 2 3 5 1 1 1 4 1 5 2 4 3 2 5 4 1 1 4 1 4 5 4 1 4 5 1 3 5 1 1 1 4 2 5 2 3 5 2 2 3 2 4 5 5 5 5 1 2 4 1 3 1 1 1 4 3 1 5 2 5 1 3 3 2 4 5 1 1 3 4 1 1 3 3 1 2 4 3 3 4 4 3 1 2 1 5 1 4 4 2 3 1 6 3 4 2 4 1 1\\n\", \"5 2\\n50 110 178 40 120\\n\", \"24 4\\n33 46 12 65 19 6 46 33 57 4 21 50 73 13 59 69 51 45 39 1 6 64 39 27\\n\", \"2 2\\n6 5\\n\", \"5 2\\n50 110 243 40 120\\n\", \"24 6\\n33 46 12 65 19 6 46 33 57 4 21 50 73 13 59 69 51 45 39 1 6 64 39 27\\n\", \"10 3\\n2787 445 184 666 2706 1999 2201 1270 847 653\\n\", \"20 20\\n924129 1131612 178964 918687 720767 695035 577430 407131 213304 810868 564435 266075 123602 376312 36680 18426 716200 121546 61834 851586\\n\", \"5 2\\n969 171 173 96 589\\n\", \"5 2\\n50 110 366 40 120\\n\", \"10 4\\n810 4412 9736 3143 3344 6029 6689 707 2513 637\\n\", \"5 2\\n969 171 173 96 547\\n\", \"24 6\\n33 46 12 65 19 6 46 33 57 4 21 50 73 13 75 69 51 45 39 1 6 64 38 27\\n\", \"24 6\\n33 46 12 65 19 6 46 33 57 4 21 50 73 13 75 69 51 45 39 1 6 22 38 27\\n\", \"24 6\\n33 46 12 65 19 6 46 33 57 4 21 50 73 13 75 69 50 45 39 1 6 22 38 27\\n\", \"10 3\\n955 445 184 666 2706 1999 1226 931 847 653\\n\", \"10 3\\n955 445 184 666 2706 1999 396 931 847 653\\n\", \"24 6\\n33 46 12 65 19 6 46 33 57 0 21 50 73 13 75 126 50 45 39 1 6 22 12 27\\n\", \"10 3\\n955 445 184 666 5092 1999 396 710 847 653\\n\", \"10 3\\n955 445 184 666 5092 1999 396 1085 847 653\\n\", \"4 1\\n2 3 4 2\\n\", \"10 4\\n810 8527 9736 3143 2341 6029 6689 707 2513 637\\n\", \"11 1\\n789 3306 3390 2290 1534 316 1080 2860 253 230 3166\\n\", \"10 3\\n2414 445 184 666 2706 1999 2201 1270 847 653\\n\", \"20 20\\n924129 939902 178964 918687 720767 695035 577430 407131 213304 810868 564435 266075 123602 376312 36680 18426 716200 121546 61834 851586\\n\", \"5 2\\n932 171 173 96 589\\n\", \"100 28\\n1 2 3 5 1 1 1 4 1 5 2 4 3 2 5 4 1 1 4 1 4 5 4 1 4 5 1 3 5 1 1 1 4 2 5 2 3 5 2 2 0 2 4 5 5 5 5 1 2 4 1 3 1 1 1 4 3 1 5 2 5 1 3 3 2 4 5 1 1 3 4 1 1 3 3 1 2 4 3 3 4 4 3 1 2 1 5 1 4 4 2 3 1 6 3 4 2 4 1 1\\n\", \"10 4\\n810 8527 9736 3143 3344 6029 6689 707 2513 637\\n\", \"11 1\\n789 3306 3390 2290 1534 316 1080 4988 253 230 3166\\n\", \"100 28\\n1 2 3 5 1 2 1 4 1 5 2 4 3 2 5 4 1 1 4 1 4 5 4 1 4 5 1 3 5 1 1 1 4 2 5 2 3 5 2 2 0 2 4 5 5 5 5 1 2 4 1 3 1 1 1 4 3 1 5 2 5 1 3 3 2 4 5 1 1 3 4 1 1 3 3 1 2 4 3 3 4 4 3 1 2 1 5 1 4 4 2 3 1 6 3 4 2 4 1 1\\n\", \"24 6\\n33 46 12 65 19 6 46 33 57 4 21 50 73 13 75 69 51 45 39 1 6 64 39 27\\n\", \"11 1\\n789 3306 3390 2290 1534 316 1080 1648 253 230 3166\\n\", \"10 3\\n2787 445 184 666 2706 1999 2201 931 847 653\\n\", \"20 20\\n924129 1131612 178964 918687 720767 695035 577430 407131 153820 810868 564435 266075 123602 376312 36680 18426 716200 121546 61834 851586\\n\", \"100 28\\n1 2 3 5 1 2 1 4 1 5 2 4 3 2 5 4 1 1 4 1 4 5 1 1 4 5 1 3 5 1 1 1 4 2 5 2 3 5 2 2 0 2 4 5 5 5 5 1 2 4 1 3 1 1 1 4 3 1 5 2 5 1 3 3 2 4 5 1 1 3 4 1 1 3 3 1 2 4 3 3 4 4 3 1 2 1 5 1 4 4 2 3 1 6 3 4 2 4 1 1\\n\", \"5 2\\n21 110 366 40 120\\n\", \"11 1\\n789 3306 3390 2290 2568 316 1080 1648 253 230 3166\\n\", \"10 3\\n513 445 184 666 2706 1999 2201 931 847 653\\n\", \"20 20\\n924129 1131612 178964 918687 720767 695035 577430 407131 153820 810868 564435 266075 81395 376312 36680 18426 716200 121546 61834 851586\\n\", \"100 28\\n1 2 3 5 1 2 1 4 1 5 2 4 3 2 5 4 1 1 4 1 4 5 1 1 4 5 1 3 5 1 1 1 4 2 5 2 3 5 2 2 0 2 4 5 5 5 5 1 2 4 1 3 1 1 1 4 3 1 5 2 5 1 3 5 2 4 5 1 1 3 4 1 1 3 3 1 2 4 3 3 4 4 3 1 2 1 5 1 4 4 2 3 1 6 3 4 2 4 1 1\\n\", \"5 2\\n21 110 366 35 120\\n\", \"11 1\\n594 3306 3390 2290 2568 316 1080 1648 253 230 3166\\n\", \"10 3\\n955 445 184 666 2706 1999 2201 931 847 653\\n\", \"20 20\\n924129 1131612 178964 918687 422285 695035 577430 407131 153820 810868 564435 266075 81395 376312 36680 18426 716200 121546 61834 851586\\n\", \"100 28\\n1 2 3 5 1 2 1 4 1 5 2 4 3 2 5 4 1 1 4 1 4 5 1 1 4 5 1 3 2 1 1 1 4 2 5 2 3 5 2 2 0 2 4 5 5 5 5 1 2 4 1 3 1 1 1 4 3 1 5 2 5 1 3 5 2 4 5 1 1 3 4 1 1 3 3 1 2 4 3 3 4 4 3 1 2 1 5 1 4 4 2 3 1 6 3 4 2 4 1 1\\n\", \"5 1\\n21 110 366 35 120\\n\", \"11 1\\n594 3306 3390 2290 4207 316 1080 1648 253 230 3166\\n\", \"100 28\\n1 2 3 5 1 2 1 4 1 5 2 4 3 2 3 4 1 1 4 1 4 5 1 1 4 5 1 3 2 1 1 1 4 2 5 2 3 5 2 2 0 2 4 5 5 5 5 1 2 4 1 3 1 1 1 4 3 1 5 2 5 1 3 5 2 4 5 1 1 3 4 1 1 3 3 1 2 4 3 3 4 4 3 1 2 1 5 1 4 4 2 3 1 6 3 4 2 4 1 1\\n\", \"5 1\\n21 111 366 35 120\\n\", \"24 6\\n33 46 12 65 19 6 46 33 57 0 21 50 73 13 75 69 50 45 39 1 6 22 38 27\\n\", \"5 1\\n21 111 366 35 55\\n\", \"24 6\\n33 46 12 65 19 6 46 33 57 0 21 50 73 13 75 69 50 45 39 1 6 22 12 27\\n\", \"10 3\\n955 445 184 666 2706 1999 396 710 847 653\\n\", \"24 6\\n33 46 12 65 3 6 46 33 57 0 21 50 73 13 75 126 50 45 39 1 6 22 12 27\\n\", \"24 6\\n33 46 12 65 3 6 46 33 57 0 21 28 73 13 75 126 50 45 39 1 6 22 12 27\\n\", \"10 3\\n955 445 184 666 5092 1999 396 453 847 653\\n\", \"5 2\\n50 110 130 40 120\\n\", \"4 1\\n2 3 4 1\\n\"], \"outputs\": [\"20\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"72\\n\", \"343\\n\", \"3707\\n\", \"921476\\n\", \"1\\n\", \"0\\n\", \"999999999\\n\", \"0\\n\", \"1122\\n\", \"707\\n\", \"9\\n\", \"9\", \"3707\", \"1122\", \"999999999\", \"0\", \"0\", \"707\", \"72\", \"921476\", \"0\", \"343\", \"2\", \"1\", \"9\\n\", \"3707\\n\", \"1100\\n\", \"999999998\\n\", \"0\\n\", \"707\\n\", \"921476\\n\", \"343\\n\", \"7\\n\", \"2\\n\", \"68\\n\", \"12\\n\", \"1\\n\", \"123\\n\", \"20\\n\", \"788\\n\", \"1113186\\n\", \"380\\n\", \"246\\n\", \"5324\\n\", \"422\\n\", \"19\\n\", \"24\\n\", \"25\\n\", \"1480\\n\", \"1751\\n\", \"76\\n\", \"4137\\n\", \"4007\\n\", \"0\\n\", \"3707\\n\", \"0\\n\", \"707\\n\", \"921476\\n\", \"343\\n\", \"2\\n\", \"3707\\n\", \"0\\n\", \"2\\n\", \"20\\n\", \"0\\n\", \"788\\n\", \"1113186\\n\", \"2\\n\", \"246\\n\", \"0\\n\", \"707\\n\", \"1113186\\n\", \"2\\n\", \"246\\n\", \"0\\n\", \"707\\n\", \"1113186\\n\", \"2\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"25\\n\", \"0\\n\", \"25\\n\", \"1751\\n\", \"76\\n\", \"76\\n\", \"4137\\n\", \"20\", \"0\"]}", "source": "taco"}
|
Evlampiy has found one more cool application to process photos. However the application has certain limitations.
Each photo i has a contrast v_{i}. In order for the processing to be truly of high quality, the application must receive at least k photos with contrasts which differ as little as possible.
Evlampiy already knows the contrast v_{i} for each of his n photos. Now he wants to split the photos into groups, so that each group contains at least k photos. As a result, each photo must belong to exactly one group.
He considers a processing time of the j-th group to be the difference between the maximum and minimum values of v_{i} in the group. Because of multithreading the processing time of a division into groups is the maximum processing time among all groups.
Split n photos into groups in a such way that the processing time of the division is the minimum possible, i.e. that the the maximum processing time over all groups as least as possible.
-----Input-----
The first line contains two integers n and k (1 ≤ k ≤ n ≤ 3·10^5) — number of photos and minimum size of a group.
The second line contains n integers v_1, v_2, ..., v_{n} (1 ≤ v_{i} ≤ 10^9), where v_{i} is the contrast of the i-th photo.
-----Output-----
Print the minimal processing time of the division into groups.
-----Examples-----
Input
5 2
50 110 130 40 120
Output
20
Input
4 1
2 3 4 1
Output
0
-----Note-----
In the first example the photos should be split into 2 groups: [40, 50] and [110, 120, 130]. The processing time of the first group is 10, and the processing time of the second group is 20. Maximum among 10 and 20 is 20. It is impossible to split the photos into groups in a such way that the processing time of division is less than 20.
In the second example the photos should be split into four groups, each containing one photo. So the minimal possible processing time of a division is 0.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"2\\n4 3\\n5 0\\n1 4\\n2 2\\n\\n5 3\\n5 2\\n4 2\\n3 1\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 543828736\\n353202854 229469066\\n105035292 19740770\\n294918734 142174357\\n944609166 419900619\\n\", \"1\\n7 7\\n875211518 78149272\\n372527826 28528254\\n777595365 608227558\\n861586350 722262664\\n996903444 323312570\\n299704754 233926739\\n778198166 197484491\\n\", \"1\\n7 1\\n107402237 913999333\\n\", \"1\\n7 7\\n10122721 121764855\\n397678435 423586551\\n203091798 455230154\\n500000000 409776311\\n421303531 418861532\\n455230153 307287064\\n417664664 419771248\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 801676035\\n787324511 873108721\\n873108720 541066719\\n873108721 372607189\\n1000000000 427003887\\n\", \"1\\n7 7\\n875211518 78149272\\n372527826 28528254\\n777595365 608227558\\n861586350 722262664\\n996903444 323312570\\n299704754 233926739\\n778198166 197484491\\n\", \"1\\n7 7\\n10122721 121764855\\n397678435 423586551\\n203091798 455230154\\n500000000 409776311\\n421303531 418861532\\n455230153 307287064\\n417664664 419771248\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 543828736\\n353202854 229469066\\n105035292 19740770\\n294918734 142174357\\n944609166 419900619\\n\", \"1\\n7 1\\n107402237 913999333\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 801676035\\n787324511 873108721\\n873108720 541066719\\n873108721 372607189\\n1000000000 427003887\\n\", \"1\\n7 7\\n875211518 78149272\\n736672479 28528254\\n777595365 608227558\\n861586350 722262664\\n996903444 323312570\\n299704754 233926739\\n778198166 197484491\\n\", \"1\\n7 7\\n10122721 111374321\\n397678435 423586551\\n203091798 455230154\\n500000000 409776311\\n421303531 418861532\\n455230153 307287064\\n417664664 419771248\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 543828736\\n353202854 229469066\\n105035292 19724161\\n294918734 142174357\\n944609166 419900619\\n\", \"1\\n11 1\\n107402237 913999333\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 801676035\\n787324511 873108721\\n1130734166 541066719\\n873108721 372607189\\n1000000000 427003887\\n\", \"1\\n1 7\\n10122721 111374321\\n397678435 423586551\\n203091798 455230154\\n500000000 409776311\\n421303531 418861532\\n455230153 307287064\\n417664664 419771248\\n\", \"1\\n11 1\\n159441243 913999333\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 801676035\\n787324511 873108721\\n1130734166 541066719\\n1309378041 372607189\\n1000000000 427003887\\n\", \"1\\n20 1\\n159441243 913999333\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 801676035\\n787324511 873108721\\n1130734166 858693746\\n1309378041 372607189\\n1000000000 427003887\\n\", \"1\\n2 7\\n10122721 111374321\\n397678435 423586551\\n203091798 455230154\\n500000000 409776311\\n421303531 418861532\\n455230153 307287064\\n193341792 419771248\\n\", \"1\\n20 1\\n110656646 913999333\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 1003477544\\n787324511 873108721\\n1130734166 858693746\\n1309378041 372607189\\n1000000000 427003887\\n\", \"1\\n20 1\\n1585117 913999333\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 1003477544\\n1087176458 873108721\\n1130734166 858693746\\n1309378041 372607189\\n1000000000 427003887\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 642651681\\n353202854 229469066\\n74370560 37695451\\n294918734 127485792\\n1819372349 419900619\\n\", \"1\\n19 1\\n1585117 913999333\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 1003477544\\n1087176458 873108721\\n597828809 858693746\\n1309378041 372607189\\n1000000000 427003887\\n\", \"1\\n2 7\\n12667397 111374321\\n397678435 423586551\\n302866284 455230154\\n500000000 409776311\\n421303531 418861532\\n587000613 307287064\\n193341792 419771248\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 1003477544\\n1087176458 873108721\\n597828809 858693746\\n244593607 372607189\\n1000000000 427003887\\n\", \"1\\n2 7\\n155406 111374321\\n397678435 316668284\\n3865652 455230154\\n500000000 782638910\\n448894432 418861532\\n587000613 307287064\\n193341792 78073600\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n1700956320 1003477544\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100000 427003887\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n1700956320 1570665517\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100001 670148084\\n\", \"1\\n4 7\\n9825 111374321\\n397678435 316668284\\n3845641 455230154\\n500000000 782638910\\n448894432 418861532\\n587000613 307287064\\n278511004 78073600\\n\", \"1\\n7 7\\n873108721 62655053\\n66631086 1631791155\\n1700956320 718789302\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100001 85719248\\n\", \"1\\n4 7\\n9825 111374321\\n397678435 316668284\\n3226030 455230154\\n907568057 782638910\\n448894432 445255633\\n587000613 307287064\\n278511004 78073600\\n\", \"1\\n7 7\\n875211518 78149272\\n736672479 28528254\\n777595365 608227558\\n861586350 722262664\\n996903444 323312570\\n240321629 233926739\\n778198166 197484491\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 543828736\\n353202854 229469066\\n74370560 19724161\\n294918734 142174357\\n944609166 419900619\\n\", \"1\\n1 7\\n10122721 111374321\\n397678435 423586551\\n203091798 455230154\\n500000000 409776311\\n421303531 418861532\\n455230153 307287064\\n193341792 419771248\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 642651681\\n353202854 229469066\\n74370560 19724161\\n294918734 142174357\\n944609166 419900619\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 642651681\\n353202854 229469066\\n74370560 37695451\\n294918734 142174357\\n944609166 419900619\\n\", \"1\\n2 7\\n12667397 111374321\\n397678435 423586551\\n203091798 455230154\\n500000000 409776311\\n421303531 418861532\\n455230153 307287064\\n193341792 419771248\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 642651681\\n353202854 229469066\\n74370560 37695451\\n294918734 127485792\\n944609166 419900619\\n\", \"1\\n2 7\\n12667397 111374321\\n397678435 423586551\\n302866284 455230154\\n500000000 409776311\\n421303531 418861532\\n455230153 307287064\\n193341792 419771248\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 642651681\\n353202854 370876802\\n74370560 37695451\\n294918734 127485792\\n1819372349 419900619\\n\", \"1\\n2 7\\n12667397 111374321\\n397678435 423586551\\n2209547 455230154\\n500000000 409776311\\n421303531 418861532\\n587000613 307287064\\n193341792 419771248\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 412854544\\n353202854 370876802\\n74370560 37695451\\n294918734 127485792\\n1819372349 419900619\\n\", \"1\\n7 7\\n873108721 195635452\\n42649954 997221147\\n873108721 1003477544\\n1087176458 873108721\\n597828809 858693746\\n244593607 405771512\\n1000000000 427003887\\n\", \"1\\n2 7\\n179729 111374321\\n397678435 423586551\\n2209547 455230154\\n500000000 409776311\\n421303531 418861532\\n587000613 307287064\\n193341792 419771248\\n\", \"1\\n1 7\\n334569692 287790954\\n828776938 450248098\\n812787473 328337325\\n353202854 370876802\\n74370560 37695451\\n294918734 127485792\\n1819372349 419900619\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n873108721 1003477544\\n1087176458 873108721\\n597828809 858693746\\n244593607 405771512\\n1000000000 427003887\\n\", \"1\\n2 7\\n179729 111374321\\n397678435 423586551\\n3865652 455230154\\n500000000 409776311\\n421303531 418861532\\n587000613 307287064\\n193341792 419771248\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n873108721 1003477544\\n1087176458 873108721\\n597828809 766334130\\n244593607 405771512\\n1000000000 427003887\\n\", \"1\\n2 7\\n179729 111374321\\n397678435 316668284\\n3865652 455230154\\n500000000 409776311\\n421303531 418861532\\n587000613 307287064\\n193341792 419771248\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n873108721 1003477544\\n1087176458 873108721\\n596405150 766334130\\n244593607 405771512\\n1000000000 427003887\\n\", \"1\\n2 7\\n179729 111374321\\n397678435 316668284\\n3865652 455230154\\n500000000 409776311\\n448894432 418861532\\n587000613 307287064\\n193341792 419771248\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n873108721 1003477544\\n1087176458 873108721\\n596405150 502327152\\n244593607 405771512\\n1000000000 427003887\\n\", \"1\\n2 7\\n155406 111374321\\n397678435 316668284\\n3865652 455230154\\n500000000 409776311\\n448894432 418861532\\n587000613 307287064\\n193341792 419771248\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n873108721 1003477544\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n1000000000 427003887\\n\", \"1\\n2 7\\n155406 111374321\\n397678435 316668284\\n3865652 455230154\\n500000000 409776311\\n448894432 418861532\\n587000613 307287064\\n193341792 717728631\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n873108721 1003477544\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000000000 427003887\\n\", \"1\\n2 7\\n155406 111374321\\n397678435 316668284\\n3865652 455230154\\n500000000 409776311\\n448894432 418861532\\n587000613 307287064\\n193341792 78073600\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n873108721 1003477544\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100000 427003887\\n\", \"1\\n2 7\\n155406 111374321\\n397678435 316668284\\n3865652 455230154\\n500000000 782638910\\n448894432 418861532\\n587000613 307287064\\n278511004 78073600\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n1700956320 1003477544\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100001 427003887\\n\", \"1\\n2 7\\n5479 111374321\\n397678435 316668284\\n3865652 455230154\\n500000000 782638910\\n448894432 418861532\\n587000613 307287064\\n278511004 78073600\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n1700956320 1003477544\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100001 670148084\\n\", \"1\\n2 7\\n5479 111374321\\n397678435 316668284\\n3845641 455230154\\n500000000 782638910\\n448894432 418861532\\n587000613 307287064\\n278511004 78073600\\n\", \"1\\n2 7\\n9825 111374321\\n397678435 316668284\\n3845641 455230154\\n500000000 782638910\\n448894432 418861532\\n587000613 307287064\\n278511004 78073600\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 997221147\\n1700956320 1570665517\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100001 85719248\\n\", \"1\\n7 7\\n873108721 195635452\\n66631086 1631791155\\n1700956320 1570665517\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100001 85719248\\n\", \"1\\n4 7\\n9825 111374321\\n397678435 316668284\\n3845641 455230154\\n500000000 782638910\\n448894432 445255633\\n587000613 307287064\\n278511004 78073600\\n\", \"1\\n7 7\\n873108721 62655053\\n66631086 1631791155\\n1700956320 1570665517\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100001 85719248\\n\", \"1\\n4 7\\n9825 111374321\\n397678435 316668284\\n3226030 455230154\\n500000000 782638910\\n448894432 445255633\\n587000613 307287064\\n278511004 78073600\\n\", \"1\\n7 7\\n873108721 62655053\\n66631086 1631791155\\n1700956320 718789302\\n1087176458 779474384\\n596405150 502327152\\n244593607 405771512\\n0000100001 168165774\\n\", \"1\\n4 7\\n9825 13827829\\n397678435 316668284\\n3226030 455230154\\n907568057 782638910\\n448894432 445255633\\n587000613 307287064\\n278511004 78073600\\n\", \"1\\n7 7\\n873108721 62655053\\n66631086 1631791155\\n1700956320 718789302\\n1087176458 779474384\\n74069455 502327152\\n244593607 405771512\\n0000100001 168165774\\n\", \"2\\n4 3\\n5 0\\n1 4\\n2 2\\n\\n5 3\\n5 2\\n4 2\\n3 1\\n\"], \"outputs\": [\"14\\n16\\n\", \"944609166\\n\", \"5734020171\\n\", \"5591398235\\n\", \"3053512092\\n\", \"6152868116\\n\", \"5734020171\\n\", \"3053512092\\n\", \"944609166\\n\", \"5591398235\\n\", \"6152868116\\n\", \"5748429986\\n\", \"3053512092\\n\", \"944609166\\n\", \"9247395567\\n\", \"6410493561\\n\", \"500000000\\n\", \"9299434573\\n\", \"6846762881\\n\", \"17525428570\\n\", \"6903717141\\n\", \"955230153\\n\", \"17476643973\\n\", \"7327131104\\n\", \"17367572444\\n\", \"7410830018\\n\", \"1819372349\\n\", \"16453573111\\n\", \"7283573396\\n\", \"1087000613\\n\", \"6977672899\\n\", \"1282638910\\n\", \"7805520498\\n\", \"11124949422\\n\", \"2847916730\\n\", \"9926543181\\n\", \"3255484787\\n\", \"5748429986\\n\", \"944609166\\n\", \"500000000\\n\", \"944609166\\n\", \"944609166\\n\", \"955230153\\n\", \"944609166\\n\", \"955230153\\n\", \"1819372349\\n\", \"1087000613\\n\", \"1819372349\\n\", \"6977672899\\n\", \"1087000613\\n\", \"1819372349\\n\", \"6977672899\\n\", \"1087000613\\n\", \"6977672899\\n\", \"1087000613\\n\", \"6977672899\\n\", \"1087000613\\n\", \"6977672899\\n\", \"1087000613\\n\", \"6977672899\\n\", \"1087000613\\n\", \"6977672899\\n\", \"1087000613\\n\", \"6977672899\\n\", \"1282638910\\n\", \"7805520498\\n\", \"1282638910\\n\", \"7805520498\\n\", \"1282638910\\n\", \"1282638910\\n\", \"11124949422\\n\", \"11124949422\\n\", \"2847916730\\n\", \"11124949422\\n\", \"2847916730\\n\", \"9926543181\\n\", \"3255484787\\n\", \"9926543181\\n\", \"14\\n16\\n\"]}", "source": "taco"}
|
Vladimir would like to prepare a present for his wife: they have an anniversary! He decided to buy her exactly $n$ flowers.
Vladimir went to a flower shop, and he was amazed to see that there are $m$ types of flowers being sold there, and there is unlimited supply of flowers of each type. Vladimir wants to choose flowers to maximize the happiness of his wife. He knows that after receiving the first flower of the $i$-th type happiness of his wife increases by $a_i$ and after receiving each consecutive flower of this type her happiness increases by $b_i$. That is, if among the chosen flowers there are $x_i > 0$ flowers of type $i$, his wife gets $a_i + (x_i - 1) \cdot b_i$ additional happiness (and if there are no flowers of type $i$, she gets nothing for this particular type).
Please help Vladimir to choose exactly $n$ flowers to maximize the total happiness of his wife.
-----Input-----
The first line contains the only integer $t$ ($1 \leq t \leq 10\,000$), the number of test cases. It is followed by $t$ descriptions of the test cases.
Each test case description starts with two integers $n$ and $m$ ($1 \le n \le 10^9$, $1 \le m \le 100\,000$), the number of flowers Vladimir needs to choose and the number of types of available flowers.
The following $m$ lines describe the types of flowers: each line contains integers $a_i$ and $b_i$ ($0 \le a_i, b_i \le 10^9$) for $i$-th available type of flowers.
The test cases are separated by a blank line. It is guaranteed that the sum of values $m$ among all test cases does not exceed $100\,000$.
-----Output-----
For each test case output a single integer: the maximum total happiness of Vladimir's wife after choosing exactly $n$ flowers optimally.
-----Example-----
Input
2
4 3
5 0
1 4
2 2
5 3
5 2
4 2
3 1
Output
14
16
-----Note-----
In the first example case Vladimir can pick 1 flower of the first type and 3 flowers of the second type, in this case the total happiness equals $5 + (1 + 2 \cdot 4) = 14$.
In the second example Vladimir can pick 2 flowers of the first type, 2 flowers of the second type, and 1 flower of the third type, in this case the total happiness equals $(5 + 1 \cdot 2) + (4 + 1 \cdot 2) + 3 = 16$.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\\n2 2 1 0\\n1 1 1 1\\n1 2 3 2\\n\", \"2\\n23 1 2 1\\n1 1 1 46\\n\", \"1\\n1 1 1 46\\n\", \"1\\n1 2 2 114514\\n\", \"1\\n114514 1 1 1919810\\n\", \"1\\n1 1 1 1919810\\n\", \"1\\n1 2 2 114514\\n\", \"1\\n1 1 1 1919810\\n\", \"1\\n1 1 1 46\\n\", \"1\\n114514 1 1 1919810\\n\", \"2\\n23 1 2 1\\n1 1 1 46\\n\", \"1\\n1 2 2 70572\\n\", \"2\\n23 1 2 1\\n2 1 1 46\\n\", \"2\\n5 1 1 2\\n2 4 1 8\\n\", \"3\\n3 2 1 0\\n1 1 1 1\\n1 2 3 2\\n\", \"2\\n5 1 1 2\\n2 4 1 2\\n\", \"1\\n2 1 4 4\\n\", \"3\\n3 2 1 0\\n1 1 1 1\\n1 2 3 6\\n\", \"2\\n23 1 2 4\\n2 1 2 0\\n\", \"3\\n2 2 1 0\\n2 1 1 1\\n1 2 3 2\\n\", \"1\\n1 1 2 1919810\\n\", \"1\\n1 1 2 46\\n\", \"1\\n35936 1 1 1919810\\n\", \"1\\n1 2 2 34959\\n\", \"1\\n1 1 2 2722288\\n\", \"1\\n1 1 2 55\\n\", \"1\\n59831 1 1 1919810\\n\", \"2\\n23 1 2 2\\n2 1 1 46\\n\", \"1\\n1 2 2 14130\\n\", \"1\\n1 0 2 2722288\\n\", \"1\\n1 1 3 55\\n\", \"1\\n59831 1 1 250092\\n\", \"2\\n23 1 2 2\\n2 1 1 18\\n\", \"1\\n1 2 2 26497\\n\", \"1\\n1 0 1 2722288\\n\", \"1\\n1 2 3 55\\n\", \"1\\n1253 1 1 250092\\n\", \"2\\n23 1 2 4\\n2 1 1 18\\n\", \"1\\n2 2 2 26497\\n\", \"1\\n1 0 2 4187757\\n\", \"1\\n1 1 4 55\\n\", \"2\\n40 1 2 4\\n2 1 1 18\\n\", \"1\\n2 1 2 26497\\n\", \"1\\n1 1 2 4187757\\n\", \"1\\n1 1 4 107\\n\", \"2\\n40 1 2 4\\n2 1 1 36\\n\", \"1\\n2 1 2 38332\\n\", \"1\\n1 2 2 4187757\\n\", \"1\\n1 2 4 107\\n\", \"2\\n40 1 2 4\\n2 2 1 36\\n\", \"1\\n2 1 2 57583\\n\", \"1\\n1 3 2 4187757\\n\", \"1\\n1 2 0 107\\n\", \"2\\n69 1 2 4\\n2 2 1 36\\n\", \"1\\n3 1 2 57583\\n\", \"1\\n1 3 3 4187757\\n\", \"2\\n69 1 2 2\\n2 2 1 36\\n\", \"1\\n3 1 2 90062\\n\", \"1\\n1 3 6 4187757\\n\", \"2\\n69 1 2 2\\n2 2 2 36\\n\", \"1\\n6 1 2 90062\\n\", \"1\\n2 3 6 4187757\\n\", \"2\\n69 1 1 2\\n2 2 2 36\\n\", \"1\\n9 1 2 90062\\n\", \"1\\n0 3 6 4187757\\n\", \"2\\n69 1 1 2\\n3 2 2 36\\n\", \"1\\n9 1 2 85317\\n\", \"1\\n0 4 6 4187757\\n\", \"2\\n69 1 1 2\\n5 2 2 36\\n\", \"1\\n9 2 2 85317\\n\", \"1\\n0 4 6 1920772\\n\", \"2\\n13 1 1 2\\n5 2 2 36\\n\", \"1\\n6 2 2 85317\\n\", \"1\\n0 7 6 1920772\\n\", \"2\\n13 1 1 2\\n5 4 2 36\\n\", \"1\\n6 2 1 85317\\n\", \"1\\n0 4 6 492087\\n\", \"2\\n13 1 1 2\\n5 4 2 18\\n\", \"1\\n0 2 1 85317\\n\", \"1\\n-1 4 6 492087\\n\", \"2\\n13 1 1 2\\n2 4 2 18\\n\", \"1\\n-1 4 6 433478\\n\", \"2\\n13 1 1 2\\n2 4 1 18\\n\", \"1\\n-1 4 6 485757\\n\", \"2\\n13 1 1 2\\n2 4 1 22\\n\", \"1\\n-1 4 12 485757\\n\", \"2\\n13 1 1 2\\n2 4 1 8\\n\", \"1\\n-2 4 12 485757\\n\", \"1\\n-2 4 23 485757\\n\", \"2\\n5 1 2 2\\n2 4 1 8\\n\", \"1\\n-2 5 23 485757\\n\", \"2\\n5 0 1 2\\n2 4 1 8\\n\", \"1\\n-2 9 23 485757\\n\", \"1\\n1 2 0 114514\\n\", \"1\\n1 1 1 2542715\\n\", \"1\\n0 1 1 46\\n\", \"1\\n114514 1 1 3451918\\n\", \"2\\n25 1 2 1\\n1 1 1 46\\n\", \"1\\n1 2 2 3245\\n\", \"1\\n1 0 2 1919810\\n\", \"1\\n1 1 2 83\\n\", \"1\\n10751 1 1 1919810\\n\", \"2\\n42 1 2 1\\n2 1 1 46\\n\", \"1\\n1 4 2 34959\\n\", \"1\\n1 1 2 4709407\\n\", \"1\\n1 0 2 55\\n\", \"1\\n66150 1 1 1919810\\n\", \"2\\n23 1 2 2\\n2 1 1 63\\n\", \"1\\n1 1 2 14130\\n\", \"1\\n59831 1 2 250092\\n\", \"2\\n23 1 2 2\\n2 0 1 18\\n\", \"1\\n0 2 2 26497\\n\", \"1\\n1 0 1 4911334\\n\", \"1\\n2 2 3 55\\n\", \"1\\n1253 1 2 250092\\n\", \"2\\n23 1 2 4\\n2 1 1 12\\n\", \"1\\n4 2 2 26497\\n\", \"1\\n1 0 0 4187757\\n\", \"1\\n1 1 4 4\\n\", \"2\\n40 1 2 2\\n2 1 1 18\\n\", \"1\\n2 1 2 38030\\n\", \"1\\n1 1 4 4187757\\n\", \"1\\n1 1 7 107\\n\", \"2\\n40 1 2 4\\n4 1 1 36\\n\", \"1\\n2 1 3 38332\\n\", \"1\\n1 2 2 3521111\\n\", \"1\\n1 2 1 107\\n\", \"2\\n40 1 2 3\\n2 2 1 36\\n\", \"1\\n2 0 2 57583\\n\", \"1\\n2 3 2 4187757\\n\", \"1\\n2 2 0 107\\n\", \"2\\n69 1 2 4\\n2 3 1 36\\n\", \"1\\n3 1 2 31466\\n\", \"1\\n1 3 3 4776678\\n\", \"2\\n69 1 2 2\\n2 1 1 36\\n\", \"1\\n3 1 3 90062\\n\", \"1\\n1 3 10 4187757\\n\", \"2\\n69 1 2 2\\n2 2 3 36\\n\", \"1\\n6 1 2 35794\\n\", \"1\\n2 3 6 7269825\\n\", \"2\\n69 1 1 2\\n2 2 3 36\\n\", \"1\\n9 2 2 90062\\n\", \"2\\n69 1 1 3\\n3 2 2 36\\n\", \"1\\n13 1 2 85317\\n\", \"1\\n0 4 12 4187757\\n\", \"2\\n69 1 1 1\\n5 2 2 36\\n\", \"1\\n9 2 1 85317\\n\", \"2\\n14 1 1 2\\n5 2 2 36\\n\", \"1\\n6 2 3 85317\\n\", \"1\\n-1 7 6 1920772\\n\", \"2\\n13 1 1 2\\n5 5 2 36\\n\", \"1\\n6 1 1 85317\\n\", \"1\\n0 3 6 492087\\n\", \"2\\n13 0 1 2\\n5 4 2 18\\n\", \"1\\n0 2 1 151830\\n\", \"1\\n0 4 12 492087\\n\", \"2\\n13 1 1 2\\n2 4 2 33\\n\", \"1\\n-1 4 5 433478\\n\", \"2\\n13 1 1 2\\n2 4 0 18\\n\", \"1\\n-1 3 6 485757\\n\", \"2\\n13 1 1 2\\n2 4 2 22\\n\", \"1\\n0 4 12 485757\\n\", \"2\\n13 1 1 2\\n2 4 1 15\\n\", \"1\\n-2 4 40 485757\\n\", \"2\\n5 1 3 2\\n2 4 1 8\\n\", \"2\\n5 0 1 2\\n2 1 1 8\\n\", \"1\\n-2 9 37 485757\\n\", \"1\\n1 1 1 4199367\\n\", \"1\\n0 1 1 27\\n\", \"1\\n114514 1 2 3451918\\n\", \"2\\n25 1 2 0\\n1 1 1 46\\n\", \"3\\n3 2 1 0\\n1 1 1 1\\n1 2 3 3\\n\", \"1\\n1 2 0 3245\\n\", \"1\\n2 1 2 83\\n\", \"1\\n10751 1 1 1585923\\n\", \"2\\n42 1 2 1\\n2 2 1 46\\n\", \"1\\n1 7 2 34959\\n\", \"1\\n1 2 2 4709407\\n\", \"1\\n68820 1 1 1919810\\n\", \"2\\n23 1 2 4\\n2 1 1 63\\n\", \"1\\n1 1 4 14130\\n\", \"1\\n63762 1 2 250092\\n\", \"2\\n23 0 2 2\\n2 1 1 18\\n\", \"1\\n0 2 2 1580\\n\", \"1\\n1 0 1 1535595\\n\", \"1\\n2 2 3 17\\n\", \"1\\n1253 1 3 250092\\n\", \"2\\n23 1 2 4\\n2 1 2 12\\n\", \"1\\n4 2 2 1832\\n\", \"2\\n40 1 2 2\\n2 0 1 18\\n\", \"1\\n1 1 2 38030\\n\", \"1\\n1 1 4 526723\\n\", \"1\\n1 2 7 107\\n\", \"2\\n40 1 2 4\\n5 1 1 36\\n\", \"1\\n2 2 3 38332\\n\", \"1\\n1 2 1 3521111\\n\", \"2\\n40 1 2 3\\n0 2 1 36\\n\", \"1\\n2 0 2 75728\\n\", \"1\\n2 3 2 4313543\\n\", \"1\\n2 2 0 22\\n\", \"2\\n39 1 2 4\\n2 3 1 36\\n\", \"1\\n3 1 2 27254\\n\", \"2\\n69 0 2 2\\n2 1 1 36\\n\", \"1\\n2 3 10 4187757\\n\", \"2\\n69 1 2 2\\n1 2 3 36\\n\", \"1\\n9 1 2 35794\\n\", \"1\\n2 3 6 10648088\\n\", \"2\\n69 1 1 2\\n2 2 3 13\\n\", \"1\\n9 2 2 73028\\n\", \"2\\n69 1 1 3\\n3 2 3 36\\n\", \"1\\n13 1 3 85317\\n\", \"3\\n2 2 1 0\\n1 1 1 1\\n1 2 3 2\\n\"], \"outputs\": [\"YES\\nNO\\nYES\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"YES\\nNO\\nYES\\n\", \"YES\\nYES\\n\", \"YES\\n\", \"YES\\nNO\\nNO\\n\", \"NO\\nYES\\n\", \"YES\\nYES\\nYES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\nYES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"NO\\nNO\\n\", \"NO\\n\", \"YES\\nNO\\nYES\\n\"]}", "source": "taco"}
|
You are given four integer values $a$, $b$, $c$ and $m$.
Check if there exists a string that contains:
$a$ letters 'A';
$b$ letters 'B';
$c$ letters 'C';
no other letters;
exactly $m$ pairs of adjacent equal letters (exactly $m$ such positions $i$ that the $i$-th letter is equal to the $(i+1)$-th one).
-----Input-----
The first line contains a single integer $t$ ($1 \le t \le 10^4$) — the number of testcases.
Each of the next $t$ lines contains the description of the testcase — four integers $a$, $b$, $c$ and $m$ ($1 \le a, b, c \le 10^8$; $0 \le m \le 10^8$).
-----Output-----
For each testcase print "YES" if there exists a string that satisfies all the requirements. Print "NO" if there are no such strings.
You may print every letter in any case you want (so, for example, the strings yEs, yes, Yes and YES will all be recognized as positive answer).
-----Examples-----
Input
3
2 2 1 0
1 1 1 1
1 2 3 2
Output
YES
NO
YES
-----Note-----
In the first testcase strings "ABCAB" or "BCABA" satisfy the requirements. There exist other possible strings.
In the second testcase there's no way to put adjacent equal letters if there's no letter that appears at least twice.
In the third testcase string "CABBCC" satisfies the requirements. There exist other possible strings.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"H 1\\nHe 4\\nC 12\\nO 16\\nF 19\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 22\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 19\\nNe 20\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)89\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 19\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nHC2\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 22\\nNe 24\\nuC 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 12\\nO 16\\nF 19\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nHC2\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHd 4\\nC 7\\nO 16\\nF 22\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHd 4\\nC 7\\nO 6\\nF 22\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHd 4\\nC 7\\nO 6\\nF 22\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 16\\nF 19\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 15\\nOe 20\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 1\\nC 12\\nO 16\\nF 19\\nNe 24\\nCu 81\\nCc 133\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 12\\nO 16\\nF 11\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nHC2\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 7\\nF 19\\nOe 9\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 8\\nC 12\\nO 16\\nF 19\\nNe 20\\nDu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)89\\n0\", \"H 1\\nHe 4\\nC 5\\nO 16\\nF 22\\nNe 24\\nCu 64\\ncC 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 1\\nC 12\\nO 16\\nF 19\\nNe 24\\nDu 81\\nCc 133\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 7\\nF 19\\nOe 9\\nCu 116\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHc 4\\nC 7\\nO 6\\nF 24\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHc 4\\nC 8\\nO 6\\nF 24\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHb 4\\nC 0\\nO 6\\nF 24\\neN 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 18\\nO 16\\nF 19\\nOe 20\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 15\\nO 16\\nF 22\\nNe 24\\nuC 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 2\\nOe 36\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHd 4\\nC 7\\nO 4\\nF 22\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 15\\nOe 20\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2D\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 1\\nC 12\\nO 25\\nF 19\\nNe 24\\nCu 81\\nCc 133\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 1\\nC 12\\nO 16\\nF 19\\nNe 13\\nCu 71\\nCc 333\\nEND_OF_FIRST_PART\\nC2H\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nHe 1\\nC 12\\nO 16\\nF 19\\nNe 24\\nDu 81\\nCc 133\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 8\\nO 16\\nF 19\\neN 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 2\\nOe 36\\nCv 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 7\\nF 19\\nNe 24\\nCu 64\\nCb 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nHe 2\\nC 12\\nO 7\\nF 19\\nOe 9\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nHe 1\\nC 12\\nO 25\\nF 19\\nNe 24\\nDu 81\\nCc 133\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 8\\nF 19\\nOe 9\\nCu 116\\nBc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nGb 7\\nC 0\\nO 6\\nF 25\\neN 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH(2\\nH((CO)2F)99\\n0\", \"H 1\\nIe 4\\nC 18\\nO 16\\nF 36\\nOe 20\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 13\\nF 19\\nNe 24\\nCu 64\\nCb 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 8\\nF 19\\nOe 9\\nuC 116\\nBc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nHe 4\\nC 12\\nO 16\\nF 19\\nNd 24\\nCu 64\\ncD 333\\nEND_OF_FIRST_PART\\nHC2\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 12\\nO 26\\nF 2\\nOe 36\\nCv 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 13\\nF 19\\nNe 24\\nuC 64\\nCb 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 8\\nO 8\\nF 19\\nOf 9\\nuC 116\\nBc 615\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\neI 5\\nC 12\\nO 16\\nF 22\\nNe 24\\nEu 64\\nCc 241\\nEND_OF_FIRST_PART\\nG2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 2\\nNe 8\\nCu 24\\nCc 409\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 2\\nNe 8\\nCu 24\\nCc 409\\nEND_OF_FIRST_PART\\nC2H\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 10\\nF 19\\nNe 16\\nuC 64\\nCb 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nDu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 1\\nO 26\\nF 2\\nOe 36\\nvC 64\\nCc 1065\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)3As\\nBu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nHe 4\\nC 12\\nO 16\\nF 2\\nNe 15\\nCu 24\\nCc 409\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 3\\nNe 20\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 24\\nF 22\\nNe 24\\nCu 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 19\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nHC2\\n(MgF)2As\\nCu(OH)2\\nH((CO)9F)29\\n0\", \"H 0\\nHe 4\\nC 12\\nO 16\\nF 19\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nHC2\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)89\\n0\", \"H 0\\nHd 4\\nC 7\\nO 8\\nF 22\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 32\\nF 19\\nNe 20\\nCu 64\\nCc 396\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 16\\nF 19\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH1C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 1\\nC 12\\nO 16\\nF 20\\nNe 24\\nCu 81\\nCc 133\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 12\\nO 16\\nF 11\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHc 4\\nC 11\\nO 6\\nF 22\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 1\\nC 12\\nO 16\\nF 4\\nNe 13\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nC2H\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 5\\nO 16\\nF 22\\nNe 24\\nCu 64\\ncC 241\\nEND_OF_FIRST_PART\\nC2H\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHd 3\\nC 7\\nO 16\\nF 22\\nNe 24\\nDu 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nDu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nHe 1\\nC 12\\nO 16\\nF 19\\nNe 44\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nIe 4\\nC 17\\nO 16\\nF 22\\nNe 24\\nCu 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nHe 4\\nC 18\\nO 16\\nF 19\\nOe 20\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 1\\nC 12\\nO 16\\nF 8\\nNe 24\\nCu 64\\nCc 83\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 16\\nF 19\\nNe 24\\nCu 76\\nCb 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 4\\nOe 50\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 8\\nO 16\\nF 22\\neN 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 1\\nOe 36\\nCv 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 7\\nF 17\\nNe 24\\nCu 64\\nCb 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 16\\nF 15\\nOe 38\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2D\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 1\\nC 12\\nO 25\\nF 19\\nNe 16\\nuC 81\\nCc 133\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 19\\nOe 50\\nCu 81\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)3\\nH((CO)2F)99\\n0\", \"H 2\\nHe 2\\nC 23\\nO 7\\nF 19\\nOe 9\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 2\\nF 19\\nNe 24\\nCu 64\\nCb 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 7\\nO 8\\nF 19\\nOe 9\\nuC 116\\nBc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 9\\nF 19\\nOe 50\\nCu 64\\nCc 482\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)3\\nH((CO)2F)99\\n0\", \"H 1\\neI 5\\nC 12\\nO 16\\nF 22\\nNe 24\\nDu 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nO((CH)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 2\\nNe 24\\nuC 24\\nCc 409\\nEND_OF_FIRST_PART\\nC2H\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 12\\nO 26\\nF 1\\nOe 36\\nCv 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nBu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 2\\nNe 8\\nCu 35\\nCc 409\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 12\\nO 26\\nF 2\\nOe 36\\nvC 64\\nCc 603\\nEND_OF_FIRST_PART\\nH2B\\n(MgF)2As\\nBu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 2\\nNe 8\\nCu 24\\nCc 409\\nEND_OF_FIRST_PART\\nC3H\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 2\\nF 2\\nNe 11\\nCu 24\\nCc 409\\nEND_OF_FIRST_PART\\nC2H\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 12\\nO 4\\nF 2\\nOe 36\\nvC 64\\nCc 1065\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)3As\\nBu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nHe 4\\nC 12\\nO 16\\nF 2\\nNe 15\\nCu 24\\nCc 409\\nEND_OF_FIRST_PART\\nC2H\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 18\\nNd 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 12\\nO 25\\nF 19\\nNe 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nHC2\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)89\\n0\", \"H 0\\nHd 4\\nC 7\\nO 8\\nF 33\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 32\\nF 19\\nNe 20\\nCu 24\\nCc 396\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHc 4\\nC 11\\nO 6\\nF 22\\nNe 24\\nuD 64\\nCc 241\\nEND_OF_FIRST_PART\\nC2H\\n(MhF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 32\\nMe 24\\nuC 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nHe 4\\nC 18\\nO 16\\nF 19\\nOe 20\\nCu 11\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\neH 4\\nC 12\\nO 16\\nF 38\\nNd 24\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nHC2\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 0\\nO 16\\nF 19\\nNe 24\\nCu 76\\nCb 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 0\\nHe 4\\nC 12\\nO 16\\nF 11\\nNe 3\\nDu 64\\nCc 17\\nEND_OF_FIRST_PART\\nHC2\\n(MgF)1As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 2\\nIe 4\\nC 12\\nO 16\\nF 22\\nNe 24\\nDu 64\\nCc 241\\nEND_OF_FIRST_PART\\nH2C\\n(MhF)2As\\nCu(OH(2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 11\\nO 16\\nF 1\\nOe 36\\nCv 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 2\\nO 14\\nF 15\\nOe 38\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2D\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\", \"H 1\\nHe 4\\nC 12\\nO 16\\nF 19\\nNe 20\\nCu 64\\nCc 333\\nEND_OF_FIRST_PART\\nH2C\\n(MgF)2As\\nCu(OH)2\\nH((CO)2F)99\\n0\"], \"outputs\": [\"14\\nUNKNOWN\\n98\\n7426\\n\", \"14\\nUNKNOWN\\n98\\n7723\\n\", \"14\\nUNKNOWN\\n98\\n6676\\n\", \"25\\nUNKNOWN\\n98\\n7426\\n\", \"14\\nUNKNOWN\\nUNKNOWN\\n7723\\n\", \"24\\nUNKNOWN\\n96\\n7425\\n\", \"9\\nUNKNOWN\\nUNKNOWN\\n6733\\n\", \"9\\nUNKNOWN\\nUNKNOWN\\n4753\\n\", \"7\\nUNKNOWN\\nUNKNOWN\\n4752\\n\", \"4\\nUNKNOWN\\n98\\n5446\\n\", \"14\\nUNKNOWN\\n98\\n7030\\n\", \"14\\nUNKNOWN\\n115\\n7426\\n\", \"24\\nUNKNOWN\\n96\\n6633\\n\", \"14\\nUNKNOWN\\n80\\n5644\\n\", \"14\\nUNKNOWN\\nUNKNOWN\\n6676\\n\", \"7\\nUNKNOWN\\n98\\n6337\\n\", \"14\\nUNKNOWN\\nUNKNOWN\\n7426\\n\", \"14\\nUNKNOWN\\n132\\n5644\\n\", \"7\\nUNKNOWN\\nUNKNOWN\\n4950\\n\", \"8\\nUNKNOWN\\nUNKNOWN\\n5148\\n\", \"0\\nUNKNOWN\\nUNKNOWN\\n3564\\n\", \"20\\nUNKNOWN\\n98\\n8614\\n\", \"17\\nUNKNOWN\\nUNKNOWN\\n8317\\n\", \"14\\nUNKNOWN\\n98\\n5743\\n\", \"7\\nUNKNOWN\\nUNKNOWN\\n4356\\n\", \"UNKNOWN\\nUNKNOWN\\n98\\n7030\\n\", \"14\\nUNKNOWN\\n133\\n9208\\n\", \"25\\nUNKNOWN\\n105\\n7426\\n\", \"16\\nUNKNOWN\\nUNKNOWN\\n7427\\n\", \"10\\nUNKNOWN\\n98\\n6634\\n\", \"14\\nUNKNOWN\\nUNKNOWN\\n5743\\n\", \"4\\nUNKNOWN\\n80\\n3664\\n\", \"16\\nUNKNOWN\\n82\\n5645\\n\", \"16\\nUNKNOWN\\nUNKNOWN\\n9209\\n\", \"14\\nUNKNOWN\\n134\\n5842\\n\", \"0\\nUNKNOWN\\nUNKNOWN\\n3663\\n\", \"20\\nUNKNOWN\\n98\\n10297\\n\", \"4\\nUNKNOWN\\n92\\n4852\\n\", \"14\\nUNKNOWN\\nUNKNOWN\\n5842\\n\", \"26\\nUNKNOWN\\n100\\n7427\\n\", \"12\\nUNKNOWN\\nUNKNOWN\\n7722\\n\", \"4\\nUNKNOWN\\nUNKNOWN\\n4852\\n\", \"10\\nUNKNOWN\\nUNKNOWN\\n5050\\n\", \"UNKNOWN\\nUNKNOWN\\nUNKNOWN\\n7723\\n\", \"14\\nUNKNOWN\\n58\\n5743\\n\", \"25\\nUNKNOWN\\n58\\n5743\\n\", \"4\\nUNKNOWN\\nUNKNOWN\\n4258\\n\", \"1\\nUNKNOWN\\nUNKNOWN\\n5544\\n\", \"16\\nUNKNOWN\\n60\\n5744\\n\", \"14\\nUNKNOWN\\n98\\n5842\\n\", \"14\\nUNKNOWN\\n114\\n9307\\n\", \"25\\nUNKNOWN\\n98\\n7860\\n\", \"24\\nUNKNOWN\\n96\\n6675\\n\", \"7\\nUNKNOWN\\nUNKNOWN\\n5148\\n\", \"14\\nUNKNOWN\\n130\\n10594\\n\", \"3\\nUNKNOWN\\n98\\n5446\\n\", \"14\\nUNKNOWN\\n115\\n7525\\n\", \"12\\nUNKNOWN\\n96\\n6633\\n\", \"11\\nUNKNOWN\\nUNKNOWN\\n5544\\n\", \"25\\nUNKNOWN\\n98\\n5941\\n\", \"11\\nUNKNOWN\\n98\\n6337\\n\", \"9\\nUNKNOWN\\n98\\n6733\\n\", \"16\\nUNKNOWN\\n100\\n7427\\n\", \"19\\nUNKNOWN\\n98\\n8713\\n\", \"22\\nUNKNOWN\\n100\\n8615\\n\", \"14\\nUNKNOWN\\n98\\n6337\\n\", \"4\\nUNKNOWN\\n110\\n5446\\n\", \"14\\nUNKNOWN\\n98\\n5941\\n\", \"10\\nUNKNOWN\\n98\\n6931\\n\", \"14\\nUNKNOWN\\nUNKNOWN\\n5644\\n\", \"4\\nUNKNOWN\\n80\\n3466\\n\", \"UNKNOWN\\nUNKNOWN\\n98\\n5050\\n\", \"14\\nUNKNOWN\\nUNKNOWN\\n9208\\n\", \"14\\nUNKNOWN\\n132\\n7426\\n\", \"27\\nUNKNOWN\\n82\\n7823\\n\", \"4\\nUNKNOWN\\n70\\n2674\\n\", \"9\\nUNKNOWN\\nUNKNOWN\\n4852\\n\", \"14\\nUNKNOWN\\n94\\n6040\\n\", \"14\\nUNKNOWN\\nUNKNOWN\\n4768\\n\", \"25\\nUNKNOWN\\nUNKNOWN\\n5743\\n\", \"12\\nUNKNOWN\\nUNKNOWN\\n7623\\n\", \"14\\nUNKNOWN\\n69\\n5743\\n\", \"UNKNOWN\\nUNKNOWN\\nUNKNOWN\\n7722\\n\", \"37\\nUNKNOWN\\n58\\n5743\\n\", \"25\\nUNKNOWN\\n30\\n2971\\n\", \"12\\nUNKNOWN\\nUNKNOWN\\n3366\\n\", \"26\\nUNKNOWN\\n60\\n5744\\n\", \"14\\nUNKNOWN\\n98\\n7327\\n\", \"24\\nUNKNOWN\\n114\\n8277\\n\", \"7\\nUNKNOWN\\nUNKNOWN\\n6237\\n\", \"14\\nUNKNOWN\\n90\\n10594\\n\", \"22\\nUNKNOWN\\nUNKNOWN\\n5544\\n\", \"14\\nUNKNOWN\\nUNKNOWN\\n8713\\n\", \"22\\nUNKNOWN\\n47\\n8615\\n\", \"25\\nUNKNOWN\\n98\\n9307\\n\", \"2\\nUNKNOWN\\n110\\n5050\\n\", \"24\\nUNKNOWN\\nUNKNOWN\\n6633\\n\", \"16\\nUNKNOWN\\nUNKNOWN\\n7724\\n\", \"13\\nUNKNOWN\\nUNKNOWN\\n5446\\n\", \"UNKNOWN\\nUNKNOWN\\n94\\n4654\\n\", \"14\\nUNKNOWN\\n98\\n7426\"]}", "source": "taco"}
|
Your mission in this problem is to write a computer program that manipulates molecular for- mulae in virtual chemistry. As in real chemistry, each molecular formula represents a molecule consisting of one or more atoms. However, it may not have chemical reality.
The following are the definitions of atomic symbols and molecular formulae you should consider.
* An atom in a molecule is represented by an atomic symbol, which is either a single capital letter or a capital letter followed by a small letter. For instance H and He are atomic symbols.
* A molecular formula is a non-empty sequence of atomic symbols. For instance, HHHeHHHe is a molecular formula, and represents a molecule consisting of four H’s and two He’s.
* For convenience, a repetition of the same sub-formula <image> where n is an integer between 2 and 99 inclusive, can be abbreviated to (X)n. Parentheses can be omitted if X is an atomic symbol. For instance, HHHeHHHe is also written as H2HeH2He, (HHHe)2, (H2He)2, or even ((H)2He)2.
The set of all molecular formulae can be viewed as a formal language. Summarizing the above description, the syntax of molecular formulae is defined as follows.
<image>
Each atom in our virtual chemistry has its own atomic weight. Given the weights of atoms, your program should calculate the weight of a molecule represented by a molecular formula. The molecular weight is defined by the sum of the weights of the constituent atoms. For instance, assuming that the atomic weights of the atoms whose symbols are H and He are 1 and 4, respectively, the total weight of a molecule represented by (H2He)2 is 12.
Input
The input consists of two parts. The first part, the Atomic Table, is composed of a number of lines, each line including an atomic symbol, one or more spaces, and its atomic weight which is a positive integer no more than 1000. No two lines include the same atomic symbol.
The first part ends with a line containing only the string END OF FIRST PART.
The second part of the input is a sequence of lines. Each line is a molecular formula, not exceeding 80 characters, and contains no spaces. A molecule contains at most 105 atoms. Some atomic symbols in a molecular formula may not appear in the Atomic Table.
The sequence is followed by a line containing a single zero, indicating the end of the input.
Output
The output is a sequence of lines, one for each line of the second part of the input. Each line contains either an integer, the molecular weight for a given molecular formula in the correspond- ing input line if all its atomic symbols appear in the Atomic Table, or UNKNOWN otherwise. No extra characters are allowed.
Example
Input
H 1
He 4
C 12
O 16
F 19
Ne 20
Cu 64
Cc 333
END_OF_FIRST_PART
H2C
(MgF)2As
Cu(OH)2
H((CO)2F)99
0
Output
14
UNKNOWN
98
7426
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.25
|
{"tests": "{\"inputs\": [[\"K\", \"A\"], [\"S\", \"A\"], [\"k\", \"s\"], [\"a\", \"a\"], [\"k\", \"A\"], [\"K\", \"a\"]], \"outputs\": [[-1], [-1], [-1], [-1], [\"k\"], [\"K\"]]}", "source": "taco"}
|
You are making your very own boardgame. The game is played by two opposing players, featuring a 6 x 6 tile system, with the players taking turns to move their pieces (similar to chess). The design is finished, now it's time to actually write and implement the features. Being the good programmer you are, you carefully plan the procedure and break the program down into smaller managable sections. You decide to start coding the logic for resolving "fights" when two pieces engage in combat on a tile.
Your boardgame features four unique pieces:
Swordsman, Cavalry, Archer and Pikeman
Each piece has unique movement and has advantages and weaknesses in combat against one of the other pieces.
Task
You must write a function ```fightResolve``` that takes the attacking and defending piece as input parameters, and returns the winning piece. It may be the case that both the attacking and defending piece belong to the same player, after which you must return an error value to indicate an illegal move.
In C++ and C, the pieces will be represented as ```chars```. Values will be case-sensitive to display ownership. Let the following char values represent each piece from their respective player.
Player 1: ```p```= Pikeman, ```k```= Cavalry, ```a```= Archer, ```s```= Swordsman
Player 2: ```P```= Pikeman, ```K```= Cavalry, ```A```= Archer, ```S```= Swordsman
The outcome of the fight between two pieces depends on which piece attacks, the type of the attacking piece and the type of the defending piece. Archers always win against swordsmens, swordsmen always win against pikemen, pikemen always win against cavalry and cavalry always win against archers. If a matchup occurs that was not previously mentioned (for example Archers vs Pikemen) the attacker will always win. This table represents the winner of each possible engagement between an attacker and a defender.
(Attacker→)
(Defender↓)
Archer
Pikeman
Swordsman
Knight
Knight
Defender
Attacker
Attacker
Attacker
Swordsman
Attacker
Defender
Attacker
Attacker
Archer
Attacker
Attacker
Defender
Attacker
Pikeman
Attacker
Attacker
Attacker
Defender
If two pieces from the same player engage in combat, i.e P vs S or k vs a, the function must return -1 to signify and illegal move. Otherwise assume that no other illegal values will be passed.
Examples
Function prototype: fightResolve(defender, attacker)
1. fightResolve('a', 'P') outputs 'P'. No interaction defined between Pikemen and Archer. Pikemen is the winner here because it is the attacking piece.
2. fightResolve('k', 'A') outputs 'k'. Knights always defeat archers, even if Archer is the attacking piece here.
3. fightResolve('S', 'A') outputs -1. Friendly units don't fight. Return -1 to indicate error.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4 5\\n1 2\\n1 3\\n1 4\\n2 3\\n2 4\", \"4 6\\n1 2\\n1 4\\n2 3\\n2 4\\n3 2\\n3 4\", \"7 13\\n6 1\\n7 2\\n3 7\\n6 5\\n3 6\\n7 4\\n3 5\\n4 1\\n3 1\\n1 5\\n1 6\\n6 2\\n2 4\\n\", \"8 12\\n6 1\\n7 5\\n2 5\\n4 1\\n6 3\\n4 3\\n5 7\\n1 3\\n5 2\\n2 7\\n4 6\\n7 2\\n\", \"10 10\\n10 6\\n9 4\\n7 8\\n1 5\\n3 10\\n2 1\\n4 9\\n5 2\\n10 3\\n6 3\\n\", \"10 4\\n7 4\\n6 8\\n2 3\\n3 8\\n\", \"2 1\\n1 2\\n\", \"5 3\\n4 2\\n2 1\\n5 4\\n\", \"10 4\\n8 4\\n9 8\\n2 8\\n8 1\\n\", \"6 7\\n5 4\\n3 1\\n4 2\\n2 1\\n5 2\\n2 3\\n2 6\\n\", \"8 7\\n6 3\\n2 4\\n3 7\\n8 2\\n4 8\\n7 6\\n3 2\\n\", \"7 8\\n4 6\\n2 1\\n2 5\\n7 4\\n7 1\\n7 2\\n1 4\\n2 4\\n\", \"9 10\\n6 4\\n7 5\\n9 3\\n7 6\\n4 8\\n4 2\\n9 8\\n1 3\\n5 1\\n4 7\\n\", \"8 5\\n3 1\\n7 5\\n2 5\\n8 6\\n1 3\\n\", \"5 7\\n4 3\\n2 5\\n2 1\\n3 2\\n1 3\\n3 4\\n1 4\\n\", \"3 6\\n1 2\\n1 3\\n2 1\\n2 3\\n3 1\\n3 2\\n\", \"5 4\\n2 5\\n4 3\\n5 2\\n5 1\\n\", \"4 6\\n1 2\\n1 3\\n1 4\\n2 3\\n2 4\\n3 4\\n\", \"7 7\\n7 3\\n5 4\\n4 7\\n5 7\\n6 3\\n5 6\\n3 4\\n\", \"9 5\\n5 8\\n7 4\\n7 2\\n9 8\\n9 5\\n\", \"7 13\\n6 1\\n7 2\\n3 7\\n6 5\\n3 6\\n7 4\\n3 5\\n4 1\\n3 1\\n1 5\\n1 6\\n4 2\\n2 4\\n\", \"10 10\\n10 6\\n9 4\\n7 8\\n1 4\\n3 10\\n2 1\\n4 9\\n5 2\\n10 3\\n6 3\\n\", \"10 4\\n7 4\\n6 7\\n2 3\\n3 8\\n\", \"8 7\\n6 3\\n2 4\\n3 3\\n8 2\\n4 8\\n7 6\\n3 2\\n\", \"8 5\\n3 1\\n7 5\\n2 5\\n8 2\\n1 3\\n\", \"3 6\\n1 2\\n1 2\\n2 1\\n2 3\\n3 1\\n3 2\\n\", \"10 10\\n10 6\\n9 4\\n7 8\\n1 4\\n6 10\\n2 1\\n1 9\\n5 1\\n10 3\\n6 3\\n\", \"7 8\\n4 6\\n3 1\\n2 5\\n7 4\\n7 1\\n7 2\\n1 4\\n2 4\\n\", \"9 10\\n6 4\\n7 7\\n9 3\\n7 6\\n4 8\\n4 2\\n9 8\\n1 3\\n5 1\\n4 7\\n\", \"5 7\\n4 3\\n2 3\\n2 1\\n3 2\\n1 3\\n3 4\\n1 4\\n\", \"4 6\\n1 2\\n1 3\\n1 4\\n2 4\\n2 4\\n3 4\\n\", \"9 5\\n5 8\\n8 4\\n7 2\\n9 8\\n9 5\\n\", \"4 6\\n1 3\\n1 4\\n2 3\\n2 4\\n3 2\\n3 4\\n\", \"7 13\\n6 1\\n7 2\\n3 7\\n6 5\\n3 6\\n7 4\\n3 7\\n4 1\\n3 1\\n1 5\\n1 6\\n4 2\\n2 4\\n\", \"10 10\\n10 6\\n9 4\\n7 8\\n1 4\\n3 10\\n2 1\\n4 9\\n5 1\\n10 3\\n6 3\\n\", \"10 4\\n7 4\\n6 7\\n2 3\\n3 1\\n\", \"8 7\\n6 3\\n2 6\\n3 3\\n8 2\\n4 8\\n7 6\\n3 2\\n\", \"7 8\\n4 6\\n3 1\\n2 5\\n7 4\\n3 1\\n7 2\\n1 4\\n2 4\\n\", \"9 10\\n6 4\\n7 8\\n9 3\\n7 6\\n4 8\\n4 2\\n9 8\\n1 3\\n5 1\\n4 7\\n\", \"9 5\\n5 8\\n8 6\\n7 2\\n9 8\\n9 5\\n\", \"4 6\\n1 3\\n1 4\\n2 3\\n2 4\\n1 2\\n3 4\\n\", \"10 10\\n10 6\\n9 4\\n7 9\\n1 4\\n3 10\\n2 1\\n4 9\\n5 1\\n10 3\\n6 3\\n\", \"10 4\\n7 4\\n6 7\\n1 3\\n3 1\\n\", \"7 8\\n4 6\\n3 1\\n2 6\\n7 4\\n3 1\\n7 2\\n1 4\\n2 4\\n\", \"7 8\\n2 6\\n3 1\\n2 6\\n7 4\\n3 1\\n7 2\\n1 4\\n2 4\\n\", \"10 10\\n3 6\\n9 4\\n7 8\\n1 5\\n3 10\\n2 1\\n4 9\\n5 2\\n10 3\\n6 3\\n\", \"8 7\\n6 3\\n2 4\\n3 7\\n8 2\\n4 8\\n5 6\\n3 2\\n\", \"7 8\\n4 6\\n2 1\\n2 5\\n7 4\\n7 1\\n5 2\\n1 4\\n2 4\\n\", \"9 10\\n6 4\\n7 5\\n9 3\\n7 6\\n4 8\\n4 2\\n9 8\\n1 3\\n5 1\\n4 6\\n\", \"3 6\\n1 1\\n1 3\\n2 1\\n2 3\\n3 1\\n3 2\\n\", \"5 4\\n2 5\\n4 3\\n3 2\\n5 1\\n\", \"17 5\\n5 8\\n7 4\\n7 2\\n9 8\\n9 5\\n\", \"4 6\\n2 2\\n1 4\\n2 3\\n2 4\\n3 2\\n3 4\\n\", \"4 5\\n1 2\\n1 3\\n1 4\\n1 3\\n2 4\\n\", \"7 13\\n6 1\\n7 2\\n3 7\\n6 5\\n3 6\\n7 4\\n3 4\\n4 1\\n3 1\\n1 5\\n1 6\\n4 2\\n2 4\\n\", \"5 7\\n4 3\\n2 3\\n2 1\\n3 2\\n1 5\\n3 4\\n1 4\\n\", \"4 6\\n1 1\\n1 4\\n2 3\\n2 4\\n3 2\\n3 4\\n\", \"10 10\\n10 6\\n9 4\\n7 8\\n1 4\\n6 10\\n2 1\\n4 9\\n5 1\\n10 3\\n6 3\\n\", \"10 4\\n7 4\\n6 7\\n2 3\\n5 1\\n\", \"7 8\\n4 6\\n3 1\\n2 5\\n7 4\\n3 1\\n3 2\\n1 4\\n2 4\\n\", \"16 5\\n5 8\\n8 6\\n7 2\\n9 8\\n9 5\\n\", \"10 10\\n10 6\\n9 4\\n7 4\\n1 4\\n3 10\\n2 1\\n4 9\\n5 1\\n10 3\\n6 3\\n\", \"10 4\\n7 4\\n6 7\\n1 3\\n2 1\\n\", \"7 8\\n4 6\\n3 1\\n2 6\\n7 4\\n6 1\\n7 2\\n1 4\\n2 4\\n\", \"10 10\\n3 6\\n9 4\\n7 8\\n1 5\\n3 10\\n3 1\\n4 9\\n5 2\\n10 3\\n6 3\\n\", \"8 7\\n6 5\\n2 4\\n3 7\\n8 2\\n4 8\\n5 6\\n3 2\\n\", \"7 8\\n4 6\\n2 1\\n3 5\\n7 4\\n7 1\\n5 2\\n1 4\\n2 4\\n\", \"13 10\\n6 4\\n7 5\\n9 3\\n7 6\\n4 8\\n4 2\\n9 8\\n1 3\\n5 1\\n4 6\\n\", \"3 6\\n2 1\\n1 3\\n2 1\\n2 3\\n3 1\\n3 2\\n\", \"5 4\\n2 5\\n1 3\\n3 2\\n5 1\\n\", \"5 7\\n4 3\\n2 3\\n2 1\\n3 2\\n1 5\\n4 4\\n1 4\\n\", \"10 4\\n7 4\\n6 7\\n2 3\\n2 1\\n\", \"13 10\\n6 4\\n7 5\\n9 3\\n7 6\\n4 8\\n4 2\\n9 8\\n1 4\\n5 1\\n4 6\\n\", \"5 4\\n2 5\\n1 4\\n3 2\\n5 1\\n\", \"10 4\\n7 5\\n6 7\\n2 3\\n2 1\\n\", \"7 13\\n6 1\\n7 2\\n1 7\\n6 5\\n3 6\\n7 4\\n3 5\\n4 1\\n3 1\\n1 5\\n1 6\\n6 2\\n2 4\\n\", \"8 12\\n6 1\\n7 5\\n2 5\\n4 1\\n6 3\\n6 3\\n5 7\\n1 3\\n5 2\\n2 7\\n4 6\\n7 2\\n\", \"10 10\\n10 5\\n9 4\\n7 8\\n1 5\\n3 10\\n2 1\\n4 9\\n5 2\\n10 3\\n6 3\\n\", \"10 4\\n7 4\\n10 8\\n2 3\\n3 8\\n\", \"5 3\\n4 2\\n2 1\\n1 4\\n\", \"10 4\\n8 4\\n9 6\\n2 8\\n8 1\\n\", \"6 7\\n5 4\\n3 1\\n4 2\\n2 1\\n5 2\\n2 3\\n3 6\\n\", \"8 7\\n6 3\\n2 4\\n3 7\\n8 2\\n4 8\\n7 4\\n3 2\\n\", \"4 6\\n1 2\\n1 4\\n2 3\\n2 4\\n3 2\\n3 4\\n\", \"4 5\\n1 2\\n1 3\\n1 4\\n2 3\\n2 4\\n\"], \"outputs\": [\"3\\n\", \"4\\n\", \"7\", \"6\", \"9\", \"4\", \"1\", \"3\", \"4\", \"5\", \"6\", \"5\", \"9\", \"5\", \"5\", \"3\", \"4\", \"3\", \"5\", \"4\", \"7\\n\", \"9\\n\", \"4\\n\", \"6\\n\", \"5\\n\", \"3\\n\", \"8\\n\", \"6\\n\", \"9\\n\", \"4\\n\", \"3\\n\", \"4\\n\", \"4\\n\", \"7\\n\", \"9\\n\", \"4\\n\", \"6\\n\", \"6\\n\", \"9\\n\", \"4\\n\", \"3\\n\", \"9\\n\", \"4\\n\", \"5\\n\", \"5\\n\", \"9\\n\", \"7\\n\", \"6\\n\", \"9\\n\", \"3\\n\", \"4\\n\", \"4\\n\", \"4\\n\", \"3\\n\", \"7\\n\", \"5\\n\", \"4\\n\", \"9\\n\", \"4\\n\", \"6\\n\", \"4\\n\", \"9\\n\", \"4\\n\", \"6\\n\", \"9\\n\", \"7\\n\", \"6\\n\", \"9\\n\", \"3\\n\", \"4\\n\", \"5\\n\", \"4\\n\", \"9\\n\", \"4\\n\", \"4\\n\", \"7\\n\", \"6\\n\", \"9\\n\", \"4\\n\", \"3\\n\", \"4\\n\", \"5\\n\", \"6\\n\", \"4\", \"3\"]}", "source": "taco"}
|
Shuseki Kingdom is the world's leading nation for innovation and technology. There are n cities in the kingdom, numbered from 1 to n.
Thanks to Mr. Kitayuta's research, it has finally become possible to construct teleportation pipes between two cities. A teleportation pipe will connect two cities unidirectionally, that is, a teleportation pipe from city x to city y cannot be used to travel from city y to city x. The transportation within each city is extremely developed, therefore if a pipe from city x to city y and a pipe from city y to city z are both constructed, people will be able to travel from city x to city z instantly.
Mr. Kitayuta is also involved in national politics. He considers that the transportation between the m pairs of city (a_{i}, b_{i}) (1 ≤ i ≤ m) is important. He is planning to construct teleportation pipes so that for each important pair (a_{i}, b_{i}), it will be possible to travel from city a_{i} to city b_{i} by using one or more teleportation pipes (but not necessarily from city b_{i} to city a_{i}). Find the minimum number of teleportation pipes that need to be constructed. So far, no teleportation pipe has been constructed, and there is no other effective transportation between cities.
-----Input-----
The first line contains two space-separated integers n and m (2 ≤ n ≤ 10^5, 1 ≤ m ≤ 10^5), denoting the number of the cities in Shuseki Kingdom and the number of the important pairs, respectively.
The following m lines describe the important pairs. The i-th of them (1 ≤ i ≤ m) contains two space-separated integers a_{i} and b_{i} (1 ≤ a_{i}, b_{i} ≤ n, a_{i} ≠ b_{i}), denoting that it must be possible to travel from city a_{i} to city b_{i} by using one or more teleportation pipes (but not necessarily from city b_{i} to city a_{i}). It is guaranteed that all pairs (a_{i}, b_{i}) are distinct.
-----Output-----
Print the minimum required number of teleportation pipes to fulfill Mr. Kitayuta's purpose.
-----Examples-----
Input
4 5
1 2
1 3
1 4
2 3
2 4
Output
3
Input
4 6
1 2
1 4
2 3
2 4
3 2
3 4
Output
4
-----Note-----
For the first sample, one of the optimal ways to construct pipes is shown in the image below: [Image]
For the second sample, one of the optimal ways is shown below: [Image]
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"tinkoff\\nzscoder\\n\", \"xxxxxx\\nxxxxxx\\n\", \"ioi\\nimo\\n\", \"abc\\naaa\\n\", \"reddit\\nabcdef\\n\", \"cbxz\\naaaa\\n\", \"bcdef\\nabbbc\\n\", \"z\\ny\\n\", \"y\\nz\\n\", \"bcdef\\nabbbc\\n\", \"z\\ny\\n\", \"reddit\\nabcdef\\n\", \"abc\\naaa\\n\", \"y\\nz\\n\", \"cbxz\\naaaa\\n\", \"fedcb\\nabbbc\\n\", \"reddit\\nbbcdef\\n\", \"cba\\naaa\\n\", \"bbxz\\naaaa\\n\", \"xxxxxw\\nxxxxxx\\n\", \"tinkogf\\nzscoder\\n\", \"ioj\\nimo\\n\", \"feddb\\nabbbc\\n\", \"bbxz\\nbaaa\\n\", \"xxxxxw\\nxxyxxx\\n\", \"thnkogf\\nzscoder\\n\", \"bbxy\\nbaba\\n\", \"xxyxxw\\nxxzxxx\\n\", \"ffoknht\\nzscoder\\n\", \"xxyxxv\\nxxzxxx\\n\", \"ffojnht\\nzscoder\\n\", \"cddff\\nbbbca\\n\", \"cdeff\\nbbbca\\n\", \"baxx\\nbaab\\n\", \"xvxyxx\\nxxzxyw\\n\", \"ffedc\\nbbbba\\n\", \"xvxyxx\\nxyzxyw\\n\", \"jjr\\njom\\n\", \"tredch\\nbfbdeb\\n\", \"axax\\naaab\\n\", \"jjr\\njnm\\n\", \"tidder\\nbbcdef\\n\", \"ipj\\nimo\\n\", \"feddb\\nacbbb\\n\", \"tidder\\nfedcbb\\n\", \"bbxy\\nbaaa\\n\", \"xxyxxw\\nxxyxxx\\n\", \"fgoknht\\nzscoder\\n\", \"ipj\\nomi\\n\", \"feddb\\nbbbca\\n\", \"reddit\\nbfcdeb\\n\", \"iqj\\nomi\\n\", \"ffddb\\nbbbca\\n\", \"reddht\\nbfcdeb\\n\", \"bbxy\\nabab\\n\", \"irj\\nomi\\n\", \"bddff\\nbbbca\\n\", \"reddht\\nbedcfb\\n\", \"bbxy\\nbaab\\n\", \"xxyxvx\\nxxzxxx\\n\", \"ffnjnht\\nzscoder\\n\", \"irj\\nmoi\\n\", \"rddeht\\nbedcfb\\n\", \"bbxx\\nbaab\\n\", \"xvxyxx\\nxxzxxx\\n\", \"ffnjnht\\nzscoeer\\n\", \"irj\\niom\\n\", \"rddeht\\nbfcdeb\\n\", \"xvxyxx\\nxxzxxw\\n\", \"ffnhnjt\\nzscoeer\\n\", \"ijr\\niom\\n\", \"ffedc\\nbbbca\\n\", \"hddert\\nbfcdeb\\n\", \"aaxx\\nbaab\\n\", \"tjnhnff\\nzscoeer\\n\", \"ijr\\njom\\n\", \"hddert\\nbfbdeb\\n\", \"xaxa\\nbaab\\n\", \"tjnhnff\\nzseocer\\n\", \"jir\\njom\\n\", \"ffedc\\nbbaba\\n\", \"treddh\\nbfbdeb\\n\", \"axax\\nbaab\\n\", \"tjnhnff\\nzseober\\n\", \"ffedc\\nbbbbb\\n\", \"tjnhnff\\nreboesz\\n\", \"xxxxxx\\nxxxxxx\\n\", \"tinkoff\\nzscoder\\n\", \"ioi\\nimo\\n\"], \"outputs\": [\"fzfsirk\\n\", \"xxxxxx\\n\", \"ioi\\n\", \"aab\\n\", \"dfdeed\\n\", \"abac\\n\", \"bccdb\\n\", \"z\\n\", \"y\\n\", \"bccdb\\n\", \"z\\n\", \"dfdeed\\n\", \"aab\\n\", \"y\\n\", \"abac\\n\", \"bccdb\", \"dfdeed\", \"aab\", \"abab\", \"wxxxxx\", \"fzgsirk\", \"ioj\", \"bdcdb\", \"bbab\", \"wyxxxx\", \"fzgshrk\", \"bbbb\", \"wzxxxx\", \"fzfshrk\", \"vzxxxx\", \"fzfshrj\", \"ccdbd\", \"ccdbe\", \"abbb\", \"vzxyxx\", \"cbdbe\", \"vzxyxy\", \"joj\", \"cfdeed\", \"abaa\", \"jnj\", \"dfdeed\", \"ioj\", \"bdcdb\", \"dfdeed\", \"bbab\", \"wyxxxx\", \"fzgshrk\", \"ioj\", \"bdcdb\", \"dfdeed\", \"ioj\", \"bdcdb\", \"dfdeed\", \"bbbb\", \"ioj\", \"bdcdb\", \"dfdeed\", \"bbbb\", \"vzxxxx\", \"fzfshrj\", \"ioj\", \"dfdeed\", \"bbbb\", \"vzxxxx\", \"fzfshrj\", \"ioj\", \"dfdeed\", \"vzxxxx\", \"fzfshrj\", \"ioj\", \"ccdbe\", \"dfdeed\", \"abab\", \"fzfshrj\", \"ioj\", \"dfdeed\", \"abab\", \"fzfshrj\", \"ioj\", \"cbdbe\", \"dfdeed\", \"abab\", \"fzfshrj\", \"cbdbe\", \"fzfshrj\", \"xxxxxx\\n\", \"fzfsirk\\n\", \"ioi\\n\"]}", "source": "taco"}
|
Oleg the client and Igor the analyst are good friends. However, sometimes they argue over little things. Recently, they started a new company, but they are having trouble finding a name for the company.
To settle this problem, they've decided to play a game. The company name will consist of n letters. Oleg and Igor each have a set of n letters (which might contain multiple copies of the same letter, the sets can be different). Initially, the company name is denoted by n question marks. Oleg and Igor takes turns to play the game, Oleg moves first. In each turn, a player can choose one of the letters c in his set and replace any of the question marks with c. Then, a copy of the letter c is removed from his set. The game ends when all the question marks has been replaced by some letter.
For example, suppose Oleg has the set of letters {i, o, i} and Igor has the set of letters {i, m, o}. One possible game is as follows :
Initially, the company name is ???.
Oleg replaces the second question mark with 'i'. The company name becomes ?i?. The set of letters Oleg have now is {i, o}.
Igor replaces the third question mark with 'o'. The company name becomes ?io. The set of letters Igor have now is {i, m}.
Finally, Oleg replaces the first question mark with 'o'. The company name becomes oio. The set of letters Oleg have now is {i}.
In the end, the company name is oio.
Oleg wants the company name to be as lexicographically small as possible while Igor wants the company name to be as lexicographically large as possible. What will be the company name if Oleg and Igor always play optimally?
A string s = s_1s_2...s_{m} is called lexicographically smaller than a string t = t_1t_2...t_{m} (where s ≠ t) if s_{i} < t_{i} where i is the smallest index such that s_{i} ≠ t_{i}. (so s_{j} = t_{j} for all j < i)
-----Input-----
The first line of input contains a string s of length n (1 ≤ n ≤ 3·10^5). All characters of the string are lowercase English letters. This string denotes the set of letters Oleg has initially.
The second line of input contains a string t of length n. All characters of the string are lowercase English letters. This string denotes the set of letters Igor has initially.
-----Output-----
The output should contain a string of n lowercase English letters, denoting the company name if Oleg and Igor plays optimally.
-----Examples-----
Input
tinkoff
zscoder
Output
fzfsirk
Input
xxxxxx
xxxxxx
Output
xxxxxx
Input
ioi
imo
Output
ioi
-----Note-----
One way to play optimally in the first sample is as follows : Initially, the company name is ???????. Oleg replaces the first question mark with 'f'. The company name becomes f??????. Igor replaces the second question mark with 'z'. The company name becomes fz?????. Oleg replaces the third question mark with 'f'. The company name becomes fzf????. Igor replaces the fourth question mark with 's'. The company name becomes fzfs???. Oleg replaces the fifth question mark with 'i'. The company name becomes fzfsi??. Igor replaces the sixth question mark with 'r'. The company name becomes fzfsir?. Oleg replaces the seventh question mark with 'k'. The company name becomes fzfsirk.
For the second sample, no matter how they play, the company name will always be xxxxxx.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"x^1-2\", \"x^1-1\", \"x^1-3\", \"x^1-4\", \"x^2-4\", \"x^1-5\", \"x^1-6\", \"x^1+6\", \"x^1+5\", \"x^1+7\", \"x^2+4x+3\", \"x^1+8\", \"x^1+9\", \"x^1+2\", \"x^1+4\", \"x^1-7\", \"x^1+3\", \"x^1-8\", \"x^1+1\", \"x^1-1\", \"x^1-2\", \"x^1-3\", \"x^1-4\", \"x^1-5\", \"x^1+5\", \"x^1+4\", \"x^1+6\", \"x^2-4\", \"x^1-6\", \"x^1+7\", \"x^1+2\", \"x^5+15x^4+85x^3+225x^2+274x+120\", \"x^2+3x+2\", \"x^3-81x^2-1882x-1800\", \"x^2-1\"], \"outputs\": [\"(x-2)\\n\", \"(x-1)\\n\", \"(x-3)\\n\", \"(x-4)\\n\", \"(x-2)(x+2)\\n\", \"(x-5)\\n\", \"(x-6)\\n\", \"(x+6)\\n\", \"(x+5)\\n\", \"(x+7)\\n\", \"(x+1)(x+3)\\n\", \"(x+8)\\n\", \"(x+9)\\n\", \"(x+2)\\n\", \"(x+4)\\n\", \"(x-7)\\n\", \"(x+3)\\n\", \"(x-8)\\n\", \"(x+1)\\n\", \"(x-1)\\n\", \"(x-2)\\n\", \"(x-3)\\n\", \"(x-4)\\n\", \"(x-5)\\n\", \"(x+5)\\n\", \"(x+4)\\n\", \"(x+6)\\n\", \"(x-2)(x+2)\\n\", \"(x-6)\\n\", \"(x+7)\\n\", \"(x+2)\\n\", \"(x+1)(x+2)(x+3)(x+4)(x+5)\", \"(x+1)(x+2)\", \"(x-100)(x+1)(x+18)\", \"(x-1)(x+1)\"]}", "source": "taco"}
|
Problem
Mr. ukuku1333 is a little sloppy, so when I expanded the product of the linear expressions of x, I couldn't figure out the original linear expression.
Given the nth degree polynomial of x, factor it into the product of the original linear expressions of x.
The nth degree polynomial of x is given by the following BNF.
<Polynomial>: = <Term> | <Polynomial> & plus; <Polynomial> | <Polynomial> − <Term>
<Term>: = x ^ <exponent> | <coefficient> x ^ <index> | <coefficient> x | <constant>
<Index>: = [2-5]
<Coefficient>: = [1-9] [0-9] *
<Constant>: = [1-9] [0-9] *
If the exponent and coefficient are omitted, it is regarded as 1.
Constraints
The input satisfies the following conditions.
* 2 ≤ n ≤ 5
* For any set of i, j such that 1 ≤ i <j ≤ m, where m is the number of terms in the given expression,
The degree of the i-th term is guaranteed to be greater than the degree of the j-th term
* It is guaranteed that the nth degree polynomial of x given can be factored into the product form of the linear expression of x.
* Absolute values of coefficients and constants are 2 × 103 or less, respectively.
* The coefficient with the highest degree is 1, which is guaranteed to be omitted.
* The original constant term of each linear expression before expansion is guaranteed to be a non-zero integer
* It is guaranteed that the original constant terms of each linear expression before expansion are different.
Input
The input is given in the following format.
S
The string S representing the nth degree polynomial of x is given on one line.
Output
Factor S into the product of a linear expression of x, and output it in ascending order of the constant term.
Insert a line break at the end of the output.
Examples
Input
x^2+3x+2
Output
(x+1)(x+2)
Input
x^2-1
Output
(x-1)(x+1)
Input
x^5+15x^4+85x^3+225x^2+274x+120
Output
(x+1)(x+2)(x+3)(x+4)(x+5)
Input
x^3-81x^2-1882x-1800
Output
(x-100)(x+1)(x+18)
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"56,65\\n97,54\\n64,-4\\n55,76\\n42,-27\\n43,80\\n87,-86\\n55,-6\\n89,34\\n5,59\\n0,0\", \"56,65\\n97,54\\n64,-4\\n55,76\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-5\\n55,76\\n42,-27\\n43,80\\n87,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,76\\n42,-27\\n34,80\\n77,-86\\n55,-6\\n89,34\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,34\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n65,-4\\n65,76\\n42,-27\\n34,80\\n77,-86\\n55,-6\\n89,34\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,65\\n97,45\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,75\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n55,76\\n42,-27\\n43,80\\n87,-76\\n55,-6\\n89,34\\n5,59\\n0,0\", \"56,65\\n97,54\\n64,-4\\n45,76\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,86\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-87\\n55,-6\\n89,34\\n85,5\\n0,0\", \"56,66\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n54,-6\\n89,34\\n85,5\\n0,0\", \"56,65\\n97,55\\n65,-4\\n65,76\\n42,-27\\n34,80\\n77,-86\\n55,-6\\n89,34\\n85,5\\n0,0\", \"56,65\\n97,45\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n55,-6\\n89,34\\n59,5\\n0,0\", \"56,75\\n97,53\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,55\\n65,-4\\n65,76\\n42,-27\\n34,80\\n77,-86\\n55,-6\\n89,33\\n85,5\\n0,0\", \"56,65\\n97,45\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n54,-6\\n89,34\\n59,5\\n0,0\", \"56,75\\n97,53\\n64,-4\\n65,77\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,65\\n97,64\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,55\\n65,-4\\n65,76\\n42,-27\\n34,80\\n77,-86\\n54,-6\\n89,33\\n85,5\\n0,0\", \"56,65\\n97,45\\n64,-5\\n55,76\\n41,-26\\n43,80\\n87,-86\\n54,-6\\n89,34\\n59,5\\n0,0\", \"56,75\\n97,53\\n64,-4\\n65,77\\n42,-27\\n43,80\\n77,-68\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,65\\n97,64\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n9,55\\n0,0\", \"56,75\\n97,53\\n64,-4\\n65,77\\n42,-27\\n43,80\\n77,-68\\n56,-4\\n89,34\\n85,5\\n0,0\", \"56,65\\n46,79\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n9,55\\n0,0\", \"56,65\\n46,79\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n55,9\\n0,0\", \"56,65\\n46,79\\n64,-4\\n57,64\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n55,9\\n0,0\", \"56,65\\n46,79\\n64,-4\\n57,64\\n42,-27\\n43,80\\n77,-86\\n54,-6\\n89,34\\n55,9\\n0,0\", \"56,65\\n46,79\\n64,-4\\n47,64\\n42,-27\\n43,80\\n77,-86\\n54,-6\\n89,34\\n55,9\\n0,0\", \"56,65\\n97,54\\n64,-4\\n67,56\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n54,-6\\n89,34\\n5,58\\n0,0\", \"56,65\\n97,54\\n65,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,65\\n97,45\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n55,-6\\n89,34\\n5,59\\n0,0\", \"76,55\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n55,75\\n42,-27\\n43,80\\n87,-76\\n55,-6\\n89,34\\n5,59\\n0,0\", \"56,65\\n97,55\\n65,-4\\n65,76\\n42,-27\\n348,0\\n77,-86\\n55,-6\\n89,34\\n85,5\\n0,0\", \"56,64\\n97,45\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n55,-6\\n89,34\\n59,5\\n0,0\", \"56,56\\n97,54\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,55\\n65,-4\\n65,76\\n42,-37\\n34,80\\n77,-86\\n55,-6\\n89,33\\n85,5\\n0,0\", \"56,75\\n97,45\\n64,-5\\n55,76\\n41,-26\\n43,80\\n87,-86\\n54,-6\\n89,34\\n59,5\\n0,0\", \"56,75\\n97,53\\n64,-4\\n65,77\\n42,-27\\n44,80\\n77,-68\\n56,-4\\n89,44\\n85,5\\n0,0\", \"46,65\\n97,64\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n9,55\\n0,0\", \"56,75\\n97,53\\n64,-4\\n65,77\\n42,-27\\n43,80\\n77,-68\\n56,-5\\n89,34\\n85,5\\n0,0\", \"56,65\\n46,79\\n64,-4\\n57,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n9,55\\n0,0\", \"56,65\\n46,79\\n64,-3\\n57,64\\n42,-27\\n43,80\\n77,-86\\n54,-6\\n89,34\\n55,9\\n0,0\", \"56,65\\n46,79\\n64,-4\\n47,64\\n42,-27\\n43,80\\n77,-76\\n54,-6\\n89,34\\n55,9\\n0,0\", \"56,65\\n97,54\\n64,-4\\n67,56\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n43,98\\n95,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n54,-6\\n43,98\\n5,58\\n0,0\", \"56,65\\n97,54\\n65,-4\\n67,56\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"55,65\\n97,45\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n55,-6\\n89,34\\n5,59\\n0,0\", \"76,55\\n97,54\\n64,-4\\n55,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,64\\n97,45\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n55,-6\\n89,35\\n59,5\\n0,0\", \"56,66\\n97,54\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"57,65\\n97,53\\n64,-4\\n65,77\\n42,-27\\n44,80\\n77,-68\\n56,-4\\n89,44\\n85,5\\n0,0\", \"46,65\\n97,64\\n64,-4\\n47,56\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n9,55\\n0,0\", \"56,65\\n97,54\\n44,-6\\n65,76\\n42,-27\\n43,80\\n77,-86\\n54,-6\\n43,98\\n5,58\\n0,0\", \"55,65\\n97,45\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n55,-7\\n89,34\\n5,59\\n0,0\", \"76,55\\n97,44\\n64,-4\\n55,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,66\\n97,53\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n44,-6\\n65,75\\n42,-27\\n43,80\\n77,-86\\n54,-6\\n43,98\\n5,58\\n0,0\", \"76,55\\n97,44\\n64,-4\\n55,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n49,84\\n85,5\\n0,0\", \"56,64\\n97,45\\n64,-5\\n56,67\\n42,-26\\n43,80\\n87,-86\\n55,-6\\n89,35\\n59,5\\n0,0\", \"55,67\\n97,44\\n64,-4\\n55,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n49,84\\n85,5\\n0,0\", \"55,67\\n97,44\\n64,-4\\n55,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n48,94\\n85,5\\n0,0\", \"56,66\\n97,53\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,24\\n95,3\\n0,0\", \"55,67\\n97,44\\n64,-4\\n55,76\\n42,-27\\n43,70\\n77,-86\\n56,-4\\n48,94\\n85,5\\n0,0\", \"55,67\\n97,44\\n64,-4\\n55,76\\n42,-27\\n42,70\\n77,-86\\n56,-4\\n48,94\\n85,5\\n0,0\", \"55,67\\n97,44\\n64,-4\\n55,76\\n42,-27\\n42,70\\n77,-86\\n56,-4\\n38,94\\n85,5\\n0,0\", \"55,67\\n97,44\\n74,-4\\n55,76\\n42,-27\\n42,70\\n77,-86\\n56,-4\\n38,94\\n85,5\\n0,0\", \"55,67\\n97,44\\n74,-4\\n55,76\\n42,-17\\n42,70\\n77,-86\\n56,-4\\n38,94\\n85,5\\n0,0\", \"55,67\\n97,44\\n74,-4\\n55,75\\n42,-17\\n42,70\\n77,-86\\n56,-4\\n38,94\\n85,5\\n0,0\", \"55,67\\n97,44\\n74,-4\\n55,75\\n42,-17\\n07,24\\n77,-86\\n56,-4\\n38,94\\n85,5\\n0,0\", \"65,67\\n97,44\\n74,-4\\n55,75\\n42,-17\\n07,24\\n77,-86\\n56,-4\\n38,94\\n85,5\\n0,0\", \"55,65\\n97,54\\n64,-4\\n55,76\\n42,-27\\n43,80\\n87,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n55,76\\n42,-27\\n53,80\\n87,-86\\n55,-6\\n89,34\\n5,59\\n0,0\", \"56,65\\n97,54\\n64,-4\\n55,76\\n42,-27\\n43,80\\n77,-86\\n65,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n65,75\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n45,79\\n64,-5\\n55,76\\n42,-27\\n43,80\\n87,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,66\\n97,54\\n64,-4\\n65,76\\n42,-27\\n34,80\\n77,-86\\n55,-6\\n89,34\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n67,56\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,34\\n85,5\\n0,0\", \"56,65\\n45,79\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,54\\n65,-4\\n65,76\\n42,-27\\n34,80\\n77,-86\\n55,-6\\n89,34\\n5,58\\n0,0\", \"56,66\\n97,54\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n67,55\\n42,-27\\n43,80\\n87,-76\\n55,-6\\n89,34\\n5,59\\n0,0\", \"56,65\\n79,54\\n64,-4\\n65,86\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n45,79\\n64,-4\\n65,76\\n42,-27\\n43,80\\n77,-87\\n55,-6\\n89,34\\n85,5\\n0,0\", \"56,65\\n97,55\\n65,-4\\n65,76\\n42,-27\\n34,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,75\\n97,53\\n64,-4\\n65,76\\n42,-27\\n43,80\\n67,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"56,65\\n45,79\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"46,65\\n97,55\\n65,-4\\n65,76\\n42,-27\\n34,80\\n77,-86\\n55,-6\\n89,33\\n85,5\\n0,0\", \"56,65\\n97,45\\n64,-5\\n55,76\\n42,-26\\n43,80\\n87,-86\\n54,-6\\n89,44\\n59,5\\n0,0\", \"56,75\\n97,53\\n64,-4\\n65,77\\n32,-27\\n43,80\\n77,-86\\n56,-4\\n89,44\\n85,5\\n0,0\", \"66,65\\n97,64\\n64,-4\\n67,54\\n42,-27\\n43,80\\n77,-86\\n55,-6\\n89,34\\n95,5\\n0,0\", \"56,65\\n97,55\\n65,-4\\n65,76\\n42,-27\\n04,83\\n77,-86\\n54,-6\\n89,33\\n85,5\\n0,0\", \"56,65\\n97,54\\n64,-4\\n55,76\\n42,-27\\n43,80\\n87,-86\\n55,-6\\n89,34\\n95,5\\n0,0\"], \"outputs\": [\"181\\n-212\\n\", \"180\\n-297\\n\", \"189\\n-301\\n\", \"190\\n-291\\n\", \"178\\n-301\\n\", \"188\\n-283\\n\", \"185\\n-293\\n\", \"172\\n-301\\n\", \"189\\n-283\\n\", \"171\\n-290\\n\", \"234\\n-283\\n\", \"108\\n-315\\n\", \"156\\n-221\\n\", \"171\\n-293\\n\", \"130\\n-294\\n\", \"194\\n-290\\n\", \"184\\n-294\\n\", \"182\\n-285\\n\", \"232\\n-247\\n\", \"115\\n-314\\n\", \"320\\n-282\\n\", \"184\\n-285\\n\", \"231\\n-246\\n\", \"109\\n-313\\n\", \"250\\n-317\\n\", \"183\\n-284\\n\", \"231\\n-245\\n\", \"43\\n-301\\n\", \"241\\n-231\\n\", \"54\\n-311\\n\", \"105\\n-281\\n\", \"97\\n-327\\n\", \"39\\n-310\\n\", \"39\\n-309\\n\", \"33\\n-302\\n\", \"308\\n-286\\n\", \"198\\n-211\\n\", \"172\\n-291\\n\", \"229\\n-193\\n\", \"228\\n-235\\n\", \"161\\n-221\\n\", \"524\\n-403\\n\", \"237\\n-243\\n\", \"369\\n-228\\n\", \"233\\n-283\\n\", \"175\\n-280\\n\", \"43\\n-302\\n\", \"241\\n-241\\n\", \"57\\n-312\\n\", \"98\\n-274\\n\", \"33\\n-309\\n\", \"0\\n-301\\n\", \"178\\n-224\\n\", \"173\\n-167\\n\", \"288\\n-282\\n\", \"229\\n-194\\n\", \"219\\n-233\\n\", \"236\\n-243\\n\", \"314\\n-288\\n\", \"105\\n-288\\n\", \"216\\n-231\\n\", \"163\\n-156\\n\", \"230\\n-193\\n\", \"280\\n-203\\n\", \"320\\n-284\\n\", \"167\\n-157\\n\", \"196\\n-157\\n\", \"285\\n-234\\n\", \"143\\n-214\\n\", \"134\\n-201\\n\", \"336\\n-278\\n\", \"165\\n-212\\n\", \"165\\n-211\\n\", \"158\\n-204\\n\", \"167\\n-208\\n\", \"130\\n-197\\n\", \"135\\n-199\\n\", \"272\\n-175\\n\", \"272\\n-165\\n\", \"171\\n-303\\n\", \"183\\n-222\\n\", \"184\\n-306\\n\", \"195\\n-302\\n\", \"-45\\n-324\\n\", \"182\\n-286\\n\", \"302\\n-280\\n\", \"-50\\n-321\\n\", \"197\\n-204\\n\", \"165\\n-293\\n\", \"264\\n-221\\n\", \"114\\n-302\\n\", \"-26\\n-321\\n\", \"181\\n-295\\n\", \"124\\n-311\\n\", \"90\\n-367\\n\", \"184\\n-295\\n\", \"221\\n-245\\n\", \"113\\n-303\\n\", \"250\\n-307\\n\", \"163\\n-254\\n\", \"171\\n-302\"]}", "source": "taco"}
|
When a boy was cleaning up after his grand father passing, he found an old paper:
<image>
In addition, other side of the paper says that "go ahead a number of steps equivalent to the first integer, and turn clockwise by degrees equivalent to the second integer".
His grand mother says that Sanbonmatsu was standing at the center of town. However, now buildings are crammed side by side and people can not walk along exactly what the paper says in. Your task is to write a program which hunts for the treature on the paper.
For simplicity, 1 step is equivalent to 1 meter. Input consists of several pairs of two integers d (the first integer) and t (the second integer) separated by a comma. Input ends with "0, 0". Your program should print the coordinate (x, y) of the end point. There is the treature where x meters to the east and y meters to the north from the center of town.
You can assume that d ≤ 100 and -180 ≤ t ≤ 180.
Input
A sequence of pairs of integers d and t which end with "0,0".
Output
Print the integer portion of x and y in a line respectively.
Example
Input
56,65
97,54
64,-4
55,76
42,-27
43,80
87,-86
55,-6
89,34
95,5
0,0
Output
171
-302
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3 2\\n1 2\\n2 3\\n2 0\\n100000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n3 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n2 3\\n5 0\\n100000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n4 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n2 3\\n2 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n2 1\\n2 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n2 1\\n3 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n2 1\\n6 0\\n100000 0\\n0 0\", \"6 2\\n1 2\\n2 3\\n5 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 1\\n3 0\\n100000 0\\n0 0\", \"3 2\\n2 2\\n2 3\\n4 0\\n100000 0\\n0 0\", \"7 2\\n1 2\\n2 4\\n5 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 3\\n5 0\\n100000 0\\n0 0\", \"9 2\\n1 2\\n2 1\\n3 0\\n100000 0\\n0 0\", \"8 2\\n1 2\\n2 3\\n6 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 3\\n6 0\\n100000 0\\n0 0\", \"9 2\\n1 2\\n2 1\\n6 0\\n100000 0\\n0 0\", \"12 2\\n1 2\\n4 3\\n6 0\\n100000 0\\n0 0\", \"12 2\\n2 2\\n4 3\\n6 0\\n100000 0\\n0 0\", \"6 2\\n2 2\\n4 3\\n6 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n2 3\\n4 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n2 1\\n1 0\\n100000 0\\n0 0\", \"7 2\\n1 4\\n1 4\\n5 0\\n100000 0\\n0 0\", \"4 2\\n4 2\\n2 3\\n2 0\\n100000 0\\n0 0\", \"6 2\\n2 2\\n4 3\\n7 0\\n100000 0\\n0 0\", \"10 2\\n1 2\\n2 3\\n4 0\\n100000 0\\n0 0\", \"7 2\\n1 2\\n3 6\\n5 0\\n000000 0\\n0 0\", \"12 2\\n1 2\\n8 3\\n0 0\\n100000 0\\n0 0\", \"4 2\\n2 2\\n4 3\\n7 0\\n100000 0\\n0 0\", \"10 2\\n1 2\\n3 3\\n4 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 3\\n7 0\\n100000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n7 0\\n100000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n6 0\\n100000 0\\n0 0\", \"3 2\\n1 2\\n2 2\\n7 0\\n000000 0\\n0 0\", \"3 2\\n1 1\\n2 3\\n1 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 2\\n7 0\\n000000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n9 0\\n100000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n10 0\\n100000 0\\n0 0\", \"4 2\\n1 1\\n2 1\\n8 0\\n100000 0\\n0 0\", \"3 2\\n1 2\\n2 2\\n0 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 2\\n7 0\\n001000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n11 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 4\\n3 0\\n000000 0\\n0 0\", \"4 2\\n1 2\\n2 3\\n7 0\\n001000 0\\n0 0\", \"4 2\\n1 2\\n2 3\\n9 0\\n001000 0\\n0 0\", \"4 2\\n1 2\\n2 2\\n9 0\\n001000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n6 0\\n000000 0\\n0 0\", \"3 2\\n2 2\\n2 3\\n6 0\\n000000 0\\n0 0\", \"3 2\\n1 2\\n2 2\\n5 0\\n000000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n8 0\\n100000 0\\n0 0\", \"7 2\\n1 1\\n2 1\\n8 0\\n100000 0\\n0 0\", \"4 2\\n1 1\\n2 3\\n6 0\\n100000 0\\n0 0\", \"4 0\\n4 1\\n2 3\\n7 0\\n100000 0\\n0 0\", \"8 2\\n1 2\\n2 2\\n7 0\\n000000 0\\n0 0\", \"3 2\\n2 2\\n2 3\\n11 0\\n000000 0\\n0 0\", \"4 0\\n4 1\\n2 3\\n3 0\\n100000 0\\n0 0\", \"7 2\\n1 2\\n3 3\\n7 0\\n001000 0\\n0 0\", \"4 2\\n1 2\\n2 3\\n13 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n2 3\\n5 0\\n000000 0\\n0 0\", \"4 2\\n1 2\\n2 2\\n9 0\\n000000 0\\n0 0\", \"4 2\\n1 2\\n2 2\\n10 0\\n000000 0\\n0 -1\", \"3 2\\n1 2\\n2 1\\n11 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 4\\n3 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 2\\n11 0\\n001000 0\\n0 0\", \"2 2\\n1 2\\n1 2\\n9 0\\n001000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n6 0\\n000010 0\\n0 0\", \"5 2\\n1 2\\n2 4\\n5 0\\n100000 0\\n0 0\", \"6 2\\n1 2\\n2 3\\n6 0\\n100000 0\\n0 0\", \"3 2\\n1 3\\n2 3\\n3 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n1 3\\n2 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n2 2\\n2 0\\n100000 0\\n0 0\", \"7 2\\n1 2\\n3 4\\n5 0\\n100000 0\\n0 0\", \"4 2\\n2 2\\n2 3\\n5 0\\n100000 0\\n0 0\", \"7 2\\n1 3\\n3 4\\n5 0\\n100000 0\\n0 0\", \"7 2\\n1 3\\n1 4\\n5 0\\n100000 0\\n0 0\", \"3 2\\n2 2\\n2 3\\n5 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 4\\n5 0\\n100000 0\\n0 0\", \"5 2\\n2 2\\n2 1\\n2 0\\n100000 0\\n0 0\", \"2 2\\n1 2\\n2 1\\n3 0\\n100000 0\\n0 0\", \"7 2\\n1 4\\n2 4\\n5 0\\n100000 0\\n0 0\", \"7 2\\n1 2\\n1 4\\n5 0\\n100000 0\\n0 0\", \"4 2\\n4 2\\n2 3\\n5 0\\n100000 0\\n0 0\", \"3 2\\n3 2\\n2 3\\n5 0\\n100000 0\\n0 0\", \"8 2\\n1 2\\n4 3\\n6 0\\n100000 0\\n0 0\", \"6 2\\n2 2\\n5 3\\n6 0\\n100000 0\\n0 0\", \"3 2\\n1 3\\n2 3\\n2 0\\n100000 0\\n0 0\", \"5 2\\n2 2\\n2 4\\n5 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n1 3\\n4 0\\n100000 0\\n0 0\", \"4 2\\n1 4\\n2 3\\n5 0\\n100000 0\\n0 0\", \"7 2\\n1 2\\n3 6\\n5 0\\n100000 0\\n0 0\", \"4 2\\n1 4\\n2 4\\n5 0\\n100000 0\\n0 0\", \"12 2\\n1 2\\n8 3\\n6 0\\n100000 0\\n0 0\", \"12 2\\n2 2\\n4 6\\n6 0\\n100000 0\\n0 0\", \"6 2\\n2 2\\n1 3\\n6 0\\n100000 0\\n0 0\", \"5 2\\n2 2\\n2 4\\n3 0\\n100000 0\\n0 0\", \"5 2\\n2 2\\n2 1\\n1 0\\n100000 0\\n0 0\", \"5 2\\n1 2\\n1 4\\n4 0\\n100000 0\\n0 0\", \"12 2\\n2 2\\n4 12\\n6 0\\n100000 0\\n0 0\", \"6 2\\n1 2\\n1 3\\n6 0\\n100000 0\\n0 0\", \"4 2\\n1 2\\n2 3\\n5 0\\n100000 0\\n0 0\", \"3 2\\n1 2\\n2 3\\n5 0\\n100000 0\\n0 0\"], \"outputs\": [\"3\\n4\\n607723520\\n\", \"3\\n8\\n607723520\\n\", \"9\\n32\\n607723520\\n\", \"3\\n16\\n607723520\\n\", \"9\\n4\\n607723520\\n\", \"17\\n4\\n607723520\\n\", \"17\\n8\\n607723520\\n\", \"17\\n64\\n607723520\\n\", \"17\\n32\\n607723520\\n\", \"9\\n8\\n607723520\\n\", \"5\\n16\\n607723520\\n\", \"33\\n32\\n607723520\\n\", \"5\\n32\\n607723520\\n\", \"257\\n8\\n607723520\\n\", \"65\\n64\\n607723520\\n\", \"5\\n64\\n607723520\\n\", \"257\\n64\\n607723520\\n\", \"1025\\n64\\n607723520\\n\", \"2049\\n64\\n607723520\\n\", \"33\\n64\\n607723520\\n\", \"9\\n16\\n607723520\\n\", \"17\\n2\\n607723520\\n\", \"65\\n32\\n607723520\\n\", \"5\\n4\\n607723520\\n\", \"33\\n128\\n607723520\\n\", \"257\\n16\\n607723520\\n\", \"33\\n32\\n\", \"1025\\n\", \"9\\n128\\n607723520\\n\", \"513\\n16\\n607723520\\n\", \"5\\n128\\n607723520\\n\", \"3\\n128\\n607723520\\n\", \"3\\n64\\n607723520\\n\", \"5\\n128\\n\", \"5\\n2\\n607723520\\n\", \"9\\n128\\n\", \"3\\n512\\n607723520\\n\", \"3\\n1024\\n607723520\\n\", \"9\\n256\\n607723520\\n\", \"5\\n\", \"9\\n128\\n688423210\\n\", \"3\\n2048\\n607723520\\n\", \"5\\n8\\n\", \"5\\n128\\n688423210\\n\", \"5\\n512\\n688423210\\n\", \"9\\n512\\n688423210\\n\", \"3\\n64\\n\", \"5\\n64\\n\", \"5\\n32\\n\", \"3\\n256\\n607723520\\n\", \"65\\n256\\n607723520\\n\", \"9\\n64\\n607723520\\n\", \"16\\n9\\n128\\n607723520\\n\", \"129\\n128\\n\", \"5\\n2048\\n\", \"16\\n9\\n8\\n607723520\\n\", \"65\\n128\\n688423210\\n\", \"5\\n8192\\n607723520\\n\", \"9\\n32\\n\", \"9\\n512\\n\", \"9\\n1024\\n\", \"5\\n2048\\n607723520\\n\", \"5\\n8\\n607723520\\n\", \"9\\n2048\\n688423210\\n\", \"3\\n512\\n688423210\\n\", \"3\\n64\\n1024\\n\", \"9\\n32\\n607723520\\n\", \"17\\n64\\n607723520\\n\", \"3\\n8\\n607723520\\n\", \"9\\n4\\n607723520\\n\", \"17\\n4\\n607723520\\n\", \"33\\n32\\n607723520\\n\", \"9\\n32\\n607723520\\n\", \"33\\n32\\n607723520\\n\", \"33\\n32\\n607723520\\n\", \"5\\n32\\n607723520\\n\", \"5\\n32\\n607723520\\n\", \"17\\n4\\n607723520\\n\", \"3\\n8\\n607723520\\n\", \"33\\n32\\n607723520\\n\", \"33\\n32\\n607723520\\n\", \"5\\n32\\n607723520\\n\", \"5\\n32\\n607723520\\n\", \"65\\n64\\n607723520\\n\", \"33\\n64\\n607723520\\n\", \"3\\n4\\n607723520\\n\", \"17\\n32\\n607723520\\n\", \"9\\n16\\n607723520\\n\", \"5\\n32\\n607723520\\n\", \"33\\n32\\n607723520\\n\", \"5\\n32\\n607723520\\n\", \"1025\\n64\\n607723520\\n\", \"2049\\n64\\n607723520\\n\", \"33\\n64\\n607723520\\n\", \"17\\n8\\n607723520\\n\", \"17\\n2\\n607723520\\n\", \"9\\n16\\n607723520\\n\", \"2049\\n64\\n607723520\\n\", \"17\\n64\\n607723520\\n\", \"5\\n32\\n607723520\\n\", \"3\\n32\\n607723520\"]}", "source": "taco"}
|
Problem Statement
"Everlasting -One-" is an award-winning online game launched this year. This game has rapidly become famous for its large number of characters you can play.
In this game, a character is characterized by attributes. There are $N$ attributes in this game, numbered $1$ through $N$. Each attribute takes one of the two states, light or darkness. It means there are $2^N$ kinds of characters in this game.
You can change your character by job change. Although this is the only way to change your character's attributes, it is allowed to change jobs as many times as you want.
The rule of job change is a bit complex. It is possible to change a character from $A$ to $B$ if and only if there exist two attributes $a$ and $b$ such that they satisfy the following four conditions:
* The state of attribute $a$ of character $A$ is light.
* The state of attribute $b$ of character $B$ is light.
* There exists no attribute $c$ such that both characters $A$ and $B$ have the light state of attribute $c$.
* A pair of attribute $(a, b)$ is compatible.
Here, we say a pair of attribute $(a, b)$ is compatible if there exists a sequence of attributes $c_1, c_2, \ldots, c_n$ satisfying the following three conditions:
* $c_1 = a$.
* $c_n = b$.
* Either $(c_i, c_{i+1})$ or $(c_{i+1}, c_i)$ is a special pair for all $i = 1, 2, \ldots, n-1$. You will be given the list of special pairs.
Since you love this game with enthusiasm, you are trying to play the game with all characters (it's really crazy). However, you have immediately noticed that one character can be changed to a limited set of characters with this game's job change rule. We say character $A$ and $B$ are essentially different if you cannot change character $A$ into character $B$ by repeating job changes.
Then, the following natural question arises; how many essentially different characters are there? Since the output may be very large, you should calculate the answer modulo $1{,}000{,}000{,}007$.
Input
The input is a sequence of datasets. The number of datasets is not more than $50$ and the total size of input is less than $5$ MB.
Each dataset is formatted as follows.
> $N$ $M$
> $a_1$ $b_1$
> :
> :
> $a_M$ $b_M$
The first line of each dataset contains two integers $N$ and $M$ ($1 \le N \le 10^5$ and $0 \le M \le 10^5$). Then $M$ lines follow. The $i$-th line contains two integers $a_i$ and $b_i$ ($1 \le a_i \lt b_i \le N$) which denote the $i$-th special pair. The input is terminated by two zeroes.
It is guaranteed that $(a_i, b_i) \ne (a_j, b_j)$ if $i \ne j$.
Output
For each dataset, output the number of essentially different characters modulo $1{,}000{,}000{,}007$.
Sample Input
3 2
1 2
2 3
5 0
100000 0
0 0
Output for the Sample Input
3
32
607723520
Example
Input
3 2
1 2
2 3
5 0
100000 0
0 0
Output
3
32
607723520
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.625
|
{"tests": "{\"inputs\": [\"1001\\n\", \"0100101110\\n\", \"0011\\n\", \"1011\\n\", \"1000\\n\", \"01\\n\", \"1010\\n\", \"0000\\n\", \"0010\\n\", \"100\\n\", \"101\\n\", \"001\\n\", \"1101111000011110111111110101100111111110111100001111011010111001101100010110000001010101101010111000\\n\", \"00\\n\", \"0\\n\", \"000\\n\", \"0001\\n\", \"1100\\n\", \"0100101111\\n\", \"0111\\n\", \"1101111000011110111111110101100111111110111100001111011010111001101100010110000001010101101010101000\\n\", \"111\\n\", \"1111\\n\", \"010111\\n\", \"11000100\\n\", \"0100101011\\n\", \"0100001011\\n\", \"1101111000001110111111110101100011111110111100001111011010111001101100010110000001010101101010101000\\n\", \"1101111000001110111111110101100011111110101100001111011010111001101100010110000001010101101010101000\\n\", \"011100\\n\", \"01001000\\n\", \"0110100011\\n\", \"1101111000001110111111110101100011011110101100001111011010111001101100010110000001010101101010101000\\n\", \"0111100011\\n\", \"1101111000001110111111110101100011011110101101001111011010111001101100010110000001010101101010101000\\n\", \"0111110011\\n\", \"1101111000001110111111110100100011011110101101001111011010111001101100010110000001010101101010101000\\n\", \"1101111000001110111111110100100011011110101101001111111010111001101100010110000001010101101010101000\\n\", \"011110\\n\", \"00111000\\n\", \"0111111111\\n\", \"111110\\n\", \"00110000\\n\", \"0101111000001110111111110100100011011110101100001111111010111001101100010110000001010101001010101000\\n\", \"1111101111\\n\", \"0101111000001110111111110100100011011110101100001111111010111001101100010110000001110101001010101000\\n\", \"1111111111\\n\", \"0101111000001110111111110100100011011110101100001111111010111001101100010110100001110101001010101000\\n\", \"00000000\\n\", \"1111111101\\n\", \"0111111101\\n\", \"0110\\n\", \"1101\\n\", \"0101\\n\", \"0100\\n\", \"1110\\n\", \"011\\n\", \"110\\n\", \"010\\n\", \"1\\n\", \"1101111000001110111111110101100111111110111100001111011010111001101100010110000001010101101010101000\\n\", \"010110\\n\", \"01000100\\n\", \"010100\\n\", \"01001100\\n\", \"0110101011\\n\", \"001100\\n\", \"01001010\\n\", \"011101\\n\", \"01011010\\n\", \"011000\\n\", \"01111010\\n\", \"0111110010\\n\", \"011010\\n\", \"01111000\\n\", \"0111110111\\n\", \"0101111000001110111111110100100011011110101101001111111010111001101100010110000001010101101010101000\\n\", \"0101111000001110111111110100100011011110101101001111111010111001101100010110000001010101001010101000\\n\", \"0111101111\\n\", \"110110\\n\", \"00110100\\n\", \"110111\\n\", \"00100000\\n\", \"100111\\n\", \"0101110000001110111111110100100011011110101100001111111010111001101100010110000001110101001010101000\\n\", \"000111\\n\", \"00001000\\n\", \"010101\\n\", \"11001100\\n\"], \"outputs\": [\"0\\n\", \"16\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"0\\n\", \"3\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"4672\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \"0\\n\", \"17\\n\", \"2\\n\", \"4669\\n\", \"1\\n\", \"3\\n\", \"4\\n\", \"12\\n\", \"14\\n\", \"23\\n\", \"4675\\n\", \"4664\\n\", \"6\\n\", \"7\\n\", \"19\\n\", \"4652\\n\", \"29\\n\", \"4636\\n\", \"25\\n\", \"4633\\n\", \"4646\\n\", \"8\\n\", \"15\\n\", \"35\\n\", \"9\\n\", \"11\\n\", \"4662\\n\", \"30\\n\", \"4665\\n\", \"36\\n\", \"4655\\n\", \"21\\n\", \"33\\n\", \"32\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"4669\\n\", \"0\\n\", \"12\\n\", \"2\\n\", \"2\\n\", \"17\\n\", \"0\\n\", \"4\\n\", \"6\\n\", \"0\\n\", \"4\\n\", \"14\\n\", \"25\\n\", \"0\\n\", \"17\\n\", \"29\\n\", \"4646\\n\", \"4646\\n\", \"29\\n\", \"0\\n\", \"2\\n\", \"4\\n\", \"15\\n\", \"4\\n\", \"4665\\n\", \"7\\n\", \"15\\n\", \"3\\n\", \"0\\n\"]}", "source": "taco"}
|
Toad Rash has a binary string s. A binary string consists only of zeros and ones.
Let n be the length of s.
Rash needs to find the number of such pairs of integers l, r that 1 ≤ l ≤ r ≤ n and there is at least one pair of integers x, k such that 1 ≤ x, k ≤ n, l ≤ x < x + 2k ≤ r, and s_x = s_{x+k} = s_{x+2k}.
Find this number of pairs for Rash.
Input
The first line contains the string s (1 ≤ |s| ≤ 300 000), consisting of zeros and ones.
Output
Output one integer: the number of such pairs of integers l, r that 1 ≤ l ≤ r ≤ n and there is at least one pair of integers x, k such that 1 ≤ x, k ≤ n, l ≤ x < x + 2k ≤ r, and s_x = s_{x+k} = s_{x+2k}.
Examples
Input
010101
Output
3
Input
11001100
Output
0
Note
In the first example, there are three l, r pairs we need to count: 1, 6; 2, 6; and 1, 5.
In the second example, there are no values x, k for the initial string, so the answer is 0.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [\"1\\n300000\\n\", \"10\\n9 8 7 7 6 4 3 2 1 1\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 1710 1689 1678 1660 1653 1648 1647 1644 1639 1635 1635 1593 1571 1534 1470 1440 1435 1389 1272 1269 1268 1263 1255 1249 1237 1174 1174 1128 1069 1067 981 979 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 676 661 639 619 616 572 568 549 501 464 455 444 443 434 430 427 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 97 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 78 78 77 77 76 76 74 72 71 71 70 69 66 64 63 63 62 60 59 59 59 55 54 53 52 52 51 49 49 49 47 47 46 46 45 44 43 42 41 41 41 40 39 38 37 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 12 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"5\\n1 1 1 1 1\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 430 426 426 423 418 417 413 409 403 402 398 388 386 384 379 373 372 366 354 353 347 344 338 325 323 323 322 310 306 303 302 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 185 184 183 174 167 167 165 163 158 139 138 132 123 122 111 91 89 88 83 62 60 58 45 39 38 34 26 3\\n\", \"3\\n3 3 3\\n\", \"10\\n99 83 62 53 47 33 24 15 10 9\\n\", \"1\\n1\\n\", \"1\\n244162\\n\", \"10\\n9 8 7 7 6 4 3 3 1 1\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 1710 1689 1678 1660 1653 1648 1647 1644 1639 1635 1635 1593 1571 1534 1470 1440 1435 1389 1272 1269 1268 1263 1255 1249 1237 1174 1174 1128 1069 1067 981 979 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 676 661 639 409 616 572 568 549 501 464 455 444 443 434 430 427 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 78 78 77 77 76 76 74 72 71 71 70 69 66 64 63 63 62 60 59 59 59 55 54 53 52 52 51 49 49 49 47 47 46 46 45 44 43 42 41 41 41 40 39 38 37 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 12 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"5\\n1 2 1 1 1\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 430 426 426 423 418 417 413 409 403 402 398 388 386 384 379 373 372 366 354 353 347 344 338 325 323 323 322 310 306 303 302 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 122 111 91 89 88 83 62 60 58 45 39 38 34 26 3\\n\", \"3\\n3 3 4\\n\", \"10\\n99 83 62 53 7 33 24 15 10 9\\n\", \"1\\n2\\n\", \"1\\n412024\\n\", \"10\\n9 8 7 7 6 4 1 3 1 1\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 1710 1689 1678 1660 1653 1648 1647 1644 1639 1635 1635 1593 1571 1534 1470 1440 1435 1389 1272 1269 1268 1263 1255 1249 1237 1174 1174 1128 1069 1067 981 979 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 676 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 78 78 77 77 76 76 74 72 71 71 70 69 66 64 63 63 62 60 59 59 59 55 54 53 52 52 51 49 49 49 47 47 46 46 45 44 43 55 41 41 41 40 39 38 37 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 12 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 430 426 426 423 418 417 413 409 403 402 398 388 386 384 379 373 372 366 354 353 347 344 338 325 323 323 322 310 306 303 302 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 122 111 91 89 88 83 10 60 58 45 39 38 34 26 3\\n\", \"3\\n1 3 4\\n\", \"10\\n99 83 62 53 7 33 24 15 8 9\\n\", \"1\\n109163\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 1710 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 1593 1571 1534 1470 1440 1435 1389 1272 1269 1268 1263 1255 1249 1237 1174 1174 1128 1069 1067 981 979 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 676 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 78 78 77 77 76 76 74 72 71 71 70 69 66 64 63 63 62 60 59 59 59 55 54 53 52 52 51 49 49 49 47 47 46 46 45 44 43 55 41 41 41 40 39 38 37 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 5 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 430 426 426 423 418 417 413 409 403 402 398 388 386 384 379 664 372 366 354 353 347 344 338 325 323 323 322 310 306 303 302 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 122 111 91 89 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 83 62 53 7 33 31 15 8 9\\n\", \"1\\n7\\n\", \"5\\n3 2 2 4 2\\n\", \"1\\n164010\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 1710 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 1593 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 1174 1174 1128 1069 1067 981 979 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 676 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 78 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 55 54 53 52 52 51 49 49 49 47 47 46 46 45 44 43 55 41 41 41 40 39 38 37 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 5 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 423 418 417 413 409 403 402 398 388 386 384 379 664 372 366 354 353 347 344 338 325 323 323 322 310 306 303 302 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 122 111 91 89 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 83 62 53 9 33 31 15 8 9\\n\", \"1\\n182029\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 1710 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 1593 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 1174 1174 406 1069 1067 981 979 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 676 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 55 54 53 52 52 51 49 49 49 47 47 46 46 45 44 43 55 41 41 41 40 39 38 37 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 5 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 423 418 417 413 409 403 402 398 388 386 384 379 664 372 366 354 353 347 344 338 325 323 323 322 310 306 303 302 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 122 111 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 165 62 53 9 33 31 15 8 9\\n\", \"1\\n263154\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 1593 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 1174 1174 406 1069 1067 981 979 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 676 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 55 54 53 52 52 51 49 49 49 47 47 46 46 45 44 43 55 41 41 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 5 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 423 418 417 413 409 403 402 398 388 386 384 379 664 372 366 354 353 347 344 338 325 323 323 322 310 306 303 302 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 204 111 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 165 62 53 9 33 31 15 14 9\\n\", \"1\\n0\\n\", \"1\\n177133\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 1593 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 979 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 676 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 44 43 55 41 41 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 5 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 423 418 417 413 409 403 402 398 388 386 384 379 664 372 366 354 353 347 344 338 325 323 323 322 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 204 111 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 165 62 53 9 33 31 15 14 16\\n\", \"1\\n145694\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 1593 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 676 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 44 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 5 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 423 418 417 413 409 403 402 398 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 322 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 204 111 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 229 62 53 9 33 31 15 14 16\\n\", \"1\\n146651\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 1593 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 403 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 257 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 52 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 14 13 5 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 423 418 417 413 409 403 402 398 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 322 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 204 011 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 229 62 53 12 33 31 15 14 16\\n\", \"1\\n15176\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 1593 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 403 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 113 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 52 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 10 13 5 12 10 9 9 8 8 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 423 418 417 413 409 403 402 398 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 110 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 167 165 163 158 139 138 132 123 204 011 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 229 62 53 12 33 33 15 14 16\\n\", \"1\\n13697\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 618 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 826 810 810 802 785 764 752 743 710 705 696 403 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 113 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 87 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 52 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 10 13 5 12 10 9 9 8 14 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 423 418 417 413 409 403 402 398 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 110 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 284 165 163 158 139 138 132 123 204 011 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 229 62 53 12 16 33 15 14 16\\n\", \"1\\n83\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 618 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 1068 810 810 802 785 764 752 743 710 705 696 403 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 113 255 228 195 184 182 177 148 129 112 91 65 31 31 22 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 149 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 52 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 10 13 5 12 10 9 9 8 14 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 386 418 417 413 409 403 402 398 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 110 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 248 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 284 165 163 158 139 138 132 123 204 011 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 229 62 53 12 16 33 15 14 3\\n\", \"1\\n15\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 618 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 1068 810 810 802 785 764 752 743 710 705 696 403 661 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 113 255 228 195 184 182 177 148 129 112 91 65 1 31 22 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 426 386 418 417 413 409 403 402 398 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 110 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 364 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 284 165 163 158 139 138 132 123 204 011 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n99 229 62 53 12 16 33 15 26 3\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 618 1571 1534 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 1068 810 810 802 785 764 752 743 710 705 696 403 352 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 113 255 228 195 184 182 177 148 129 112 91 65 1 31 22 3\\n\", \"100\\n100 100 99 98 138 92 92 92 92 91 89 149 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 52 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 10 13 5 12 10 10 9 8 14 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 797 386 418 417 413 409 403 402 398 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 110 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 364 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 284 165 163 158 139 138 132 123 204 011 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 618 1571 2703 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 1068 810 810 802 785 764 752 743 710 705 696 403 352 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 113 255 228 195 184 182 177 148 129 112 91 65 1 31 22 3\\n\", \"100\\n100 100 99 98 138 92 92 92 92 91 89 149 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 88 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 52 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 10 13 5 12 10 10 9 8 14 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 797 386 418 417 413 409 403 402 426 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 110 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 364 248 247 243 236 235 233 227 227 223 208 204 200 196 192 191 289 184 183 174 167 284 165 163 158 139 138 132 123 204 011 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"100\\n1980 1932 1906 1898 1892 1883 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 618 1571 2703 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 1068 810 810 802 785 764 752 743 710 705 696 403 352 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 113 255 228 195 184 182 177 148 129 112 91 65 1 52 22 3\\n\", \"100\\n100 100 99 98 138 92 92 92 92 91 89 149 87 169 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 88 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 52 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 10 13 5 12 10 10 9 8 14 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 797 386 418 417 413 409 403 402 426 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 110 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 364 248 247 243 236 235 157 227 227 223 208 204 200 196 192 191 289 184 183 174 167 284 165 163 158 139 138 132 123 204 011 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n137 245 62 53 12 16 35 15 26 3\\n\", \"100\\n1980 1932 1906 1898 1892 896 1877 1858 1842 1833 1777 2810 1689 1678 1660 1653 1648 1647 1644 1639 1635 43 618 1571 2703 1470 1440 1435 2525 1272 1269 1268 1263 1255 1249 1237 780 1174 406 1069 1067 981 1838 979 951 915 911 906 863 1068 810 810 802 785 764 752 743 710 705 696 403 352 639 409 616 572 568 549 501 464 455 444 443 434 430 72 399 386 345 339 324 324 309 300 113 255 228 195 184 182 177 148 129 112 91 65 1 52 22 3\\n\", \"100\\n100 100 99 98 138 92 92 92 92 91 89 149 9 169 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 88 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 52 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 10 13 5 12 10 10 9 8 14 8 7 4 3 3 3\\n\", \"100\\n494 493 483 483 482 479 469 455 452 448 446 437 436 22 426 797 386 418 417 413 409 403 402 426 388 386 384 379 368 372 366 354 353 347 344 338 325 323 323 110 310 306 303 408 299 296 291 290 288 285 281 274 258 254 253 250 364 281 247 243 236 235 157 227 227 223 208 204 200 196 192 191 289 184 183 174 167 284 165 163 158 139 138 132 123 204 011 91 116 88 83 10 60 58 45 39 38 34 26 3\\n\", \"10\\n137 338 62 53 12 16 35 15 26 3\\n\", \"5\\n3 2 2 2 2\\n\", \"5\\n0 2 1 1 1\\n\", \"1\\n4\\n\", \"5\\n3 1 2 2 2\\n\", \"10\\n9 8 8 7 6 4 1 3 1 1\\n\", \"5\\n0 2 0 1 1\\n\", \"3\\n2 3 4\\n\", \"1\\n5\\n\", \"5\\n3 2 2 4 3\\n\", \"1\\n6\\n\", \"5\\n3 2 2 1 3\\n\", \"5\\n3 2 0 1 3\\n\", \"100\\n100 100 99 98 109 92 92 92 92 91 89 149 87 87 86 85 84 82 82 81 81 80 79 34 78 77 77 76 76 74 72 71 71 70 69 66 122 63 63 62 60 59 59 59 32 54 53 52 52 51 49 49 49 47 47 46 46 45 52 43 55 41 60 41 40 39 38 5 37 36 31 29 25 23 22 22 21 21 20 17 17 16 15 15 14 10 13 5 12 10 10 9 8 14 8 7 4 3 3 3\\n\", \"5\\n3 2 2 2 1\\n\"], \"outputs\": [\"150000\\n\", \"23\\n\", \"46496\\n\", \"2545\\n\", \"2\\n\", \"13710\\n\", \"4\\n\", \"216\\n\", \"0\\n\", \"122081\\n\", \"24\\n\", \"46391\\n\", \"2551\\n\", \"2\\n\", \"13762\\n\", \"5\\n\", \"196\\n\", \"1\\n\", \"206012\\n\", \"23\\n\", \"46213\\n\", \"2558\\n\", \"13736\\n\", \"4\\n\", \"195\\n\", \"54581\\n\", \"45417\\n\", \"2554\\n\", \"13882\\n\", \"199\\n\", \"3\\n\", \"6\\n\", \"82005\\n\", \"45985\\n\", \"2583\\n\", \"13678\\n\", \"200\\n\", \"91014\\n\", \"45624\\n\", \"2561\\n\", \"13692\\n\", \"241\\n\", \"131577\\n\", \"46174\\n\", \"2545\\n\", \"13733\\n\", \"244\\n\", \"0\\n\", \"88566\\n\", \"45977\\n\", \"2533\\n\", \"13786\\n\", \"248\\n\", \"72847\\n\", \"46407\\n\", \"2542\\n\", \"13638\\n\", \"280\\n\", \"73325\\n\", \"46270\\n\", \"2546\\n\", \"13588\\n\", \"281\\n\", \"7588\\n\", \"46198\\n\", \"2544\\n\", \"13482\\n\", \"282\\n\", \"6848\\n\", \"45711\\n\", \"2547\\n\", \"13540\\n\", \"274\\n\", \"41\\n\", \"45832\\n\", \"2578\\n\", \"13522\\n\", \"267\\n\", \"7\\n\", \"45817\\n\", \"13580\\n\", \"273\\n\", \"45662\\n\", \"2592\\n\", \"13766\\n\", \"46246\\n\", \"2601\\n\", \"13780\\n\", \"46256\\n\", \"2642\\n\", \"13742\\n\", \"301\\n\", \"45762\\n\", \"2603\\n\", \"13759\\n\", \"348\\n\", \"5\\n\", \"2\\n\", \"2\\n\", \"5\\n\", \"24\\n\", \"2\\n\", \"4\\n\", \"2\\n\", \"6\\n\", \"3\\n\", \"5\\n\", \"4\\n\", \"2578\\n\", \"4\\n\"]}", "source": "taco"}
|
You are given a Young diagram.
Given diagram is a histogram with n columns of lengths a_1, a_2, …, a_n (a_1 ≥ a_2 ≥ … ≥ a_n ≥ 1).
<image> Young diagram for a=[3,2,2,2,1].
Your goal is to find the largest number of non-overlapping dominos that you can draw inside of this histogram, a domino is a 1 × 2 or 2 × 1 rectangle.
Input
The first line of input contain one integer n (1 ≤ n ≤ 300 000): the number of columns in the given histogram.
The next line of input contains n integers a_1, a_2, …, a_n (1 ≤ a_i ≤ 300 000, a_i ≥ a_{i+1}): the lengths of columns.
Output
Output one integer: the largest number of non-overlapping dominos that you can draw inside of the given Young diagram.
Example
Input
5
3 2 2 2 1
Output
4
Note
Some of the possible solutions for the example:
<image> <image>
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[2863311530], [128], [131], [2], [24082], [0], [85], [1024], [1], [1365]], \"outputs\": [[true], [true], [true], [true], [true], [false], [false], [false], [false], [false]]}", "source": "taco"}
|
~~~if-not:ruby,python
Return `1` when *any* odd bit of `x` equals 1; `0` otherwise.
~~~
~~~if:ruby,python
Return `true` when *any* odd bit of `x` equals 1; `false` otherwise.
~~~
Assume that:
* `x` is an unsigned, 32-bit integer;
* the bits are zero-indexed (the least significant bit is position 0)
## Examples
```
2 --> 1 (true) because at least one odd bit is 1 (2 = 0b10)
5 --> 0 (false) because none of the odd bits are 1 (5 = 0b101)
170 --> 1 (true) because all of the odd bits are 1 (170 = 0b10101010)
```
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"7\\n1 2\\n2 3\\n2 4\\n4 5\\n4 6\\n5 7\\n\", \"7\\n1 2\\n1 3\\n2 4\\n2 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n2 3\\n3 4\\n3 5\\n3 6\\n3 7\\n\", \"7\\n1 2\\n2 3\\n2 4\\n2 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n2 3\\n2 4\\n2 5\\n2 6\\n1 7\\n\", \"7\\n1 2\\n4 6\\n2 4\\n3 5\\n3 2\\n3 7\\n\", \"7\\n1 2\\n2 3\\n2 4\\n2 5\\n1 6\\n1 7\\n\", \"7\\n1 2\\n2 3\\n2 4\\n3 5\\n3 6\\n3 7\\n\", \"7\\n1 2\\n2 3\\n2 4\\n3 5\\n1 6\\n1 7\\n\", \"7\\n1 2\\n4 3\\n2 4\\n2 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n2 6\\n2 4\\n3 5\\n3 6\\n3 7\\n\", \"7\\n1 2\\n2 6\\n2 4\\n3 5\\n3 2\\n3 7\\n\", \"7\\n1 2\\n2 3\\n2 6\\n4 5\\n4 6\\n5 7\\n\", \"7\\n1 2\\n1 3\\n2 4\\n2 5\\n2 6\\n1 7\\n\", \"7\\n1 2\\n4 3\\n1 4\\n2 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n2 4\\n3 4\\n3 5\\n3 6\\n3 7\\n\", \"7\\n1 3\\n2 3\\n2 4\\n2 5\\n1 6\\n1 7\\n\", \"7\\n1 2\\n1 6\\n2 4\\n2 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n1 3\\n2 4\\n2 5\\n2 6\\n2 7\\n\", \"7\\n1 2\\n2 3\\n2 6\\n4 5\\n7 6\\n5 7\\n\", \"7\\n1 2\\n1 6\\n2 4\\n2 5\\n3 6\\n2 7\\n\", \"7\\n1 2\\n1 3\\n2 4\\n2 5\\n1 6\\n2 7\\n\", \"7\\n1 2\\n2 3\\n2 6\\n4 1\\n7 6\\n5 7\\n\", \"7\\n1 2\\n1 3\\n2 4\\n2 5\\n1 6\\n3 7\\n\", \"7\\n1 2\\n2 3\\n2 6\\n4 2\\n7 6\\n5 7\\n\", \"7\\n1 2\\n2 3\\n3 4\\n3 5\\n4 6\\n3 7\\n\", \"7\\n1 2\\n1 3\\n2 4\\n1 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n2 3\\n2 4\\n3 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n2 3\\n2 4\\n3 5\\n3 6\\n4 7\\n\", \"7\\n1 2\\n2 6\\n2 4\\n3 5\\n3 2\\n4 7\\n\", \"7\\n1 2\\n2 3\\n2 6\\n4 5\\n4 6\\n6 7\\n\", \"7\\n1 3\\n2 3\\n1 4\\n2 5\\n1 6\\n1 7\\n\", \"7\\n1 4\\n1 6\\n2 4\\n2 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n2 3\\n2 6\\n4 5\\n7 2\\n5 7\\n\", \"7\\n1 2\\n4 3\\n2 6\\n4 2\\n7 6\\n5 7\\n\", \"7\\n1 4\\n2 3\\n2 4\\n3 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n2 6\\n2 4\\n2 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n4 3\\n2 4\\n2 5\\n2 6\\n1 7\\n\", \"7\\n1 2\\n2 3\\n1 4\\n3 5\\n1 6\\n1 7\\n\", \"7\\n1 2\\n2 6\\n2 4\\n2 5\\n3 6\\n3 7\\n\", \"7\\n1 2\\n2 6\\n2 4\\n3 5\\n3 1\\n3 7\\n\", \"7\\n1 2\\n4 3\\n1 4\\n4 5\\n3 6\\n1 7\\n\", \"7\\n1 2\\n2 7\\n3 4\\n3 5\\n3 6\\n3 7\\n\", \"7\\n1 2\\n2 3\\n3 4\\n3 5\\n3 6\\n4 7\\n\", \"7\\n1 2\\n1 6\\n2 4\\n3 5\\n3 2\\n4 7\\n\", \"7\\n1 2\\n2 3\\n3 4\\n3 5\\n3 6\\n3 7\\n\", \"7\\n1 2\\n2 3\\n2 4\\n4 5\\n4 6\\n5 7\\n\", \"7\\n1 2\\n1 3\\n2 4\\n2 5\\n3 6\\n1 7\\n\"], \"outputs\": [\"2\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"1\\n\", \"2\\n\", \"0\\n\"]}", "source": "taco"}
|
You are given an undirected tree consisting of $n$ vertices. An undirected tree is a connected undirected graph with $n - 1$ edges.
Your task is to add the minimum number of edges in such a way that the length of the shortest path from the vertex $1$ to any other vertex is at most $2$. Note that you are not allowed to add loops and multiple edges.
-----Input-----
The first line contains one integer $n$ ($2 \le n \le 2 \cdot 10^5$) — the number of vertices in the tree.
The following $n - 1$ lines contain edges: edge $i$ is given as a pair of vertices $u_i, v_i$ ($1 \le u_i, v_i \le n$). It is guaranteed that the given edges form a tree. It is guaranteed that there are no loops and multiple edges in the given edges.
-----Output-----
Print a single integer — the minimum number of edges you have to add in order to make the shortest distance from the vertex $1$ to any other vertex at most $2$. Note that you are not allowed to add loops and multiple edges.
-----Examples-----
Input
7
1 2
2 3
2 4
4 5
4 6
5 7
Output
2
Input
7
1 2
1 3
2 4
2 5
3 6
1 7
Output
0
Input
7
1 2
2 3
3 4
3 5
3 6
3 7
Output
1
-----Note-----
The tree corresponding to the first example: [Image] The answer is $2$, some of the possible answers are the following: $[(1, 5), (1, 6)]$, $[(1, 4), (1, 7)]$, $[(1, 6), (1, 7)]$.
The tree corresponding to the second example: [Image] The answer is $0$.
The tree corresponding to the third example: [Image] The answer is $1$, only one possible way to reach it is to add the edge $(1, 3)$.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"oyh\\nni\\nEND_OF_TEXT\\nf\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nnh\\nEND_OF_TEXT\\nf\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nnh\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nnh\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\np\\np\\ne\\nx\\n`\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyo\\noh\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\np\\np\\ne\\nx\\n`\\nk\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nni\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"iyo\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\ny\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"hyn\\nnh\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\np\\np\\ne\\nx\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nnj\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"iyo\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\nz\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"hyp\\noh\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\no\\np\\ne\\nx\\n`\\nk\\ny\\ny\\nn\\ny\\n-\", \"oyh\\njn\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"oyi\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\nz\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\nd\\nh\\nf\\nj\\np\\no\\ne\\ny\\na\\ni\\ny\\ny\\nn\\ny\\n-\", \"oyi\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\n{\\na\\nj\\ny\\nz\\nn\\ny\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nj\\np\\np\\ne\\ny\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"hyn\\nni\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nj\\np\\np\\ne\\ny\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\nx\\n-\", \"oyh\\nni\\nEND_OF_TEXT\\nf\\nd\\nf\\nf\\nk\\np\\np\\nf\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nin\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyn\\noh\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\no\\np\\ne\\nx\\n`\\nk\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nnj\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\nz\\ny\\nn\\ny\\n-\", \"oyh\\njn\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\nz\\nn\\ny\\n-\", \"hyo\\nmi\\nEND_OF_TEXT\\nf\\nd\\nh\\nf\\nj\\np\\np\\ne\\ny\\na\\ni\\ny\\ny\\nn\\ny\\n-\", \"nyi\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\n{\\na\\nj\\ny\\nz\\nn\\ny\\n-\", \"hyo\\nin\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nj\\np\\np\\ne\\ny\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"hyn\\nni\\nEND_OF_TEXT\\nd\\nc\\nh\\ne\\nj\\np\\np\\ne\\ny\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\nz\\ny\\nn\\nx\\n-\", \"oyh\\nin\\nEND_OF_TEXT\\nf\\nd\\nf\\nf\\nk\\np\\np\\nf\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nin\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\nx\\nn\\ny\\n-\", \"oyh\\nnh\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\np\\np\\ne\\nx\\na\\nl\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nni\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nk\\np\\np\\ne\\nz\\n`\\nk\\ny\\ny\\nn\\ny\\n-\", \"iyo\\nni\\nEND_OF_TEXT\\nf\\nd\\nh\\nf\\nj\\np\\no\\ne\\ny\\na\\ni\\ny\\ny\\nn\\ny\\n-\", \"oyi\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nj\\np\\np\\ne\\n{\\na\\nj\\ny\\nx\\nn\\ny\\n-\", \"nyi\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\nd\\n{\\na\\nj\\ny\\nz\\nn\\ny\\n-\", \"hyo\\nin\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nk\\np\\np\\ne\\ny\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"yhn\\nni\\nEND_OF_TEXT\\nd\\nc\\nh\\ne\\nj\\np\\np\\ne\\ny\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"oyh\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\nz\\ny\\nn\\nx\\n-\", \"gyo\\nin\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nk\\np\\np\\ne\\ny\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nni\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nj\\np\\np\\ne\\nz\\n_\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyn\\nho\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\no\\np\\ne\\nx\\n_\\nk\\ny\\nx\\nn\\ny\\n-\", \"nyi\\noi\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\nd\\n{\\na\\nj\\ny\\nz\\nm\\ny\\n-\", \"gyo\\nin\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nk\\np\\np\\ne\\ny\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"oyh\\nni\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nj\\np\\np\\ne\\nz\\n_\\nk\\nx\\ny\\nn\\ny\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\nd\\ni\\nf\\nj\\np\\no\\nd\\nz\\nb\\ni\\ny\\ny\\no\\ny\\n-\", \"nyi\\noi\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nl\\np\\np\\nd\\n{\\na\\nj\\ny\\nz\\nm\\ny\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\ne\\ni\\ne\\nk\\np\\np\\ne\\ny\\n`\\nj\\nx\\ny\\nn\\ny\\n-\", \"gyp\\nin\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nk\\np\\np\\ne\\ny\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"oyg\\nni\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nj\\np\\np\\ne\\nz\\n_\\nk\\nx\\ny\\nn\\ny\\n-\", \"yhn\\nni\\nEND_OF_TEXT\\ne\\nc\\ni\\ne\\nj\\np\\np\\ne\\ny\\nb\\nj\\nz\\ny\\nn\\ny\\n-\", \"gyp\\nin\\nEND_OF_TEXT\\nf\\nc\\ng\\ne\\nk\\np\\np\\ne\\nx\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"oyg\\nni\\nEND_OF_TEXT\\ng\\ne\\ng\\nf\\nj\\np\\np\\ne\\nz\\n_\\nk\\nx\\ny\\nn\\ny\\n-\", \"hyn\\nhn\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nl\\no\\np\\ne\\nx\\n_\\nk\\ny\\nz\\no\\ny\\n-\", \"gyp\\nin\\nEND_OF_TEXT\\nf\\nc\\ng\\ne\\nk\\np\\no\\ne\\nx\\na\\nj\\nz\\nx\\nn\\ny\\n-\", \"hyn\\ngn\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nl\\no\\np\\ne\\nx\\n_\\nk\\ny\\nz\\no\\ny\\n-\", \"pyg\\nin\\nEND_OF_TEXT\\nf\\nc\\ng\\ne\\nk\\np\\no\\ne\\nx\\na\\nj\\nz\\nx\\nn\\ny\\n-\", \"pyg\\nin\\nEND_OF_TEXT\\nf\\nc\\ng\\ne\\nk\\np\\no\\ne\\nx\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"hyn\\ngn\\nEND_OF_TEXT\\nd\\nd\\nf\\ng\\nl\\no\\np\\ne\\nx\\n^\\nk\\ny\\nz\\no\\ny\\n-\", \"hyn\\ngn\\nEND_OF_TEXT\\nd\\nd\\nf\\ng\\nl\\no\\np\\ne\\nx\\n^\\nl\\ny\\nz\\no\\ny\\n-\", \"hyn\\nng\\nEND_OF_TEXT\\nd\\nd\\nf\\ng\\nn\\no\\no\\ne\\nx\\n^\\nk\\ny\\ny\\no\\nw\\n-\", \"hyn\\nng\\nEND_OF_TEXT\\nd\\nc\\nf\\ng\\nn\\no\\no\\ne\\nx\\n^\\nk\\ny\\ny\\no\\nv\\n-\", \"hoy\\nni\\nEND_OF_TEXT\\nf\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nni\\nEND_OF_TEXT\\nf\\nd\\nf\\nf\\nj\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\nc\\ng\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hoy\\noh\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\no\\np\\ne\\nx\\n`\\nk\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nnj\\nEND_OF_TEXT\\ng\\nd\\ne\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nnh\\nEND_OF_TEXT\\nf\\nd\\nh\\nf\\nj\\np\\no\\ne\\ny\\na\\ni\\ny\\ny\\nn\\ny\\n-\", \"hyp\\nho\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\no\\np\\ne\\nw\\n`\\nk\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nni\\nEND_OF_TEXT\\nf\\nd\\nh\\nf\\nj\\np\\np\\ne\\ny\\na\\ni\\ny\\ny\\nn\\ny\\n-\", \"hyn\\nin\\nEND_OF_TEXT\\ne\\nc\\nh\\ne\\nj\\np\\np\\ne\\ny\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"hyo\\nin\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\nd\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\", \"gyo\\nnh\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nk\\np\\np\\ne\\nx\\na\\nl\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nin\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\n`\\nk\\ny\\ny\\nn\\ny\\n-\", \"iyo\\nin\\nEND_OF_TEXT\\nf\\nd\\nh\\nf\\nk\\np\\no\\ne\\ny\\na\\ni\\ny\\ny\\nn\\ny\\n-\", \"hyo\\nnj\\nEND_OF_TEXT\\nf\\nd\\nh\\nf\\nj\\np\\no\\ne\\nz\\na\\ni\\ny\\ny\\nn\\ny\\n-\", \"nyi\\nnh\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\n{\\na\\nj\\ny\\nz\\nn\\ny\\n-\", \"hyo\\nin\\nEND_OF_TEXT\\nf\\nd\\nh\\nf\\nj\\np\\np\\ne\\nx\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"hzn\\nni\\nEND_OF_TEXT\\ne\\nc\\nh\\ne\\ni\\np\\np\\ne\\ny\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\no\\nd\\ny\\nb\\nj\\ny\\ny\\nn\\nz\\n-\", \"hyp\\nni\\nEND_OF_TEXT\\nf\\nd\\nh\\nf\\nj\\np\\no\\ne\\nz\\na\\ni\\ny\\ny\\no\\ny\\n-\", \"oyi\\nin\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nj\\np\\np\\ne\\n{\\na\\nj\\ny\\nx\\nn\\ny\\n-\", \"hyo\\nio\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nk\\np\\np\\ne\\ny\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"oyh\\nin\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\nz\\ny\\nn\\nx\\n-\", \"gyo\\nin\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nk\\np\\np\\nd\\ny\\na\\nj\\ny\\ny\\nn\\ny\\n-\", \"ozh\\nni\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nk\\np\\np\\ne\\nx\\na\\nk\\nz\\ny\\nn\\nx\\n-\", \"yhn\\nni\\nEND_OF_TEXT\\nd\\nc\\ni\\ne\\nj\\nq\\np\\nd\\ny\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"oyh\\nin\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nj\\np\\np\\ne\\nz\\n_\\nk\\nx\\ny\\nn\\ny\\n-\", \"oyh\\nni\\nEND_OF_TEXT\\nf\\nd\\ni\\nf\\nj\\np\\no\\nd\\nz\\nb\\ni\\ny\\ny\\no\\ny\\n-\", \"nyi\\noi\\nEND_OF_TEXT\\nf\\nd\\ng\\nf\\nl\\np\\np\\nc\\n{\\na\\nj\\ny\\nz\\nm\\ny\\n-\", \"oyg\\nin\\nEND_OF_TEXT\\ng\\nd\\nf\\nf\\nj\\np\\np\\ne\\nz\\n_\\nk\\nx\\ny\\nn\\ny\\n-\", \"gyp\\nin\\nEND_OF_TEXT\\nf\\nc\\ng\\ne\\nk\\np\\np\\nf\\ny\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"hxn\\nho\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nl\\no\\np\\ne\\nx\\n_\\nk\\ny\\nz\\no\\ny\\n-\", \"gxp\\nin\\nEND_OF_TEXT\\nf\\nc\\ng\\ne\\nk\\np\\np\\ne\\nx\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"hyn\\nho\\nEND_OF_TEXT\\nf\\nd\\nf\\nf\\nl\\no\\np\\ne\\nx\\n_\\nk\\ny\\nz\\no\\ny\\n-\", \"gyp\\nin\\nEND_OF_TEXT\\nf\\nd\\ng\\ne\\nk\\np\\no\\ne\\nx\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"hyo\\ngn\\nEND_OF_TEXT\\ne\\nd\\nf\\nf\\nl\\no\\np\\ne\\nx\\n_\\nk\\ny\\nz\\no\\ny\\n-\", \"hyn\\ngn\\nEND_OF_TEXT\\ne\\nc\\nf\\nf\\nl\\no\\np\\ne\\nx\\n^\\nk\\ny\\nz\\no\\ny\\n-\", \"qyg\\nin\\nEND_OF_TEXT\\nf\\nc\\nh\\ne\\nk\\np\\no\\ne\\nx\\na\\nj\\nz\\ny\\nn\\ny\\n-\", \"hyn\\nfn\\nEND_OF_TEXT\\nd\\nd\\nf\\ng\\nm\\no\\no\\ne\\nx\\n_\\nl\\ny\\ny\\nn\\nx\\n-\", \"hyo\\nni\\nEND_OF_TEXT\\nf\\nd\\nf\\nf\\nk\\np\\np\\ne\\ny\\na\\nk\\ny\\ny\\nn\\ny\\n-\"], \"outputs\": [\"ohniohni\\nohni\\n\", \"honhhonh\\nhonh\\n\", \"honi\\n\\n\\n\\n\\n\", \"hyonhhyonhhyonh\\n\", \"hyonh\\n\", \"hyooh\\n\", \"yhni\\n\\n\\n\\n\\n\", \"ioni\\n\\n\\n\\n\\n\", \"hynnhhynnhhynnh\\n\", \"yhnj\\n\\n\\n\\n\\n\", \"\\n\\n\\nioni\\n\", \"hypoh\\n\", \"yhjn\\n\\n\\n\\n\\n\", \"\\n\\n\\noini\\n\", \"ho\\nni\\n\", \"\\n\\noini\\n\", \"hyo\\nni\\n\", \"hyn\\nni\\n\", \"honi\\n\\n\\n\\n\", \"onihonih\\nonih\\n\", \"hoin\\n\\n\\n\\n\\n\", \"hynoh\\n\", \"yhnj\\n\\n\\n\\n\", \"yhjn\\n\\n\\n\\n\", \"ho\\nmi\\n\", \"\\n\\nnini\\n\", \"hyo\\nin\\n\", \"yn\\nni\\n\", \"honi\\n\\n\\n\", \"oinhoinh\\noinh\\n\", \"hoin\\n\\n\\n\\n\", \"oyhnh\\n\", \"yhni\\n\\n\\n\\n\", \"io\\nni\\n\", \"oi\\nni\\n\", \"\\n\\nini\\n\", \"hyoin\\n\\n\\n\\n\\n\", \"hn\\nni\\n\", \"ohni\\n\\n\\n\", \"gyoin\\n\\n\\n\\n\\n\", \"yh\\n\\n\\nni\\n\", \"hynho\\n\", \"\\n\\nioi\\n\", \"gyoin\\n\\n\\n\\n\", \"yh\\n\\nni\\n\", \"o\\nni\\n\", \"i\\noi\\n\", \"hyoni\\n\\n\\n\\n\", \"gypin\\n\\n\\n\\n\", \"yg\\n\\nni\\n\", \"yhn\\nni\\n\", \"\\n\\ngypin\\n\", \"oyg\\n\\nni\\n\", \"hynhn\\n\", \"\\ngypin\\n\", \"hyngn\\n\", \"\\npygin\\n\", \"\\n\\npygin\\n\", \"n\\n\\ngn\\n\", \"n\\ngn\\n\", \"n\\nng\\n\", \"yn\\nng\\n\", \"hynihyni\\nhyni\\n\", \"ohoh\\nohni\\n\", \"hyohyo\\nhyoni\\n\", \"hoyoh\\n\", \"yhnjyhnj\\nyhnj\\n\", \"ho\\nnh\\n\", \"hypho\\n\", \"oh\\nni\\n\", \"hyn\\nin\\n\", \"\\noinoinoin\\n\", \"gyonh\\n\", \"yhin\\n\\n\\n\\n\\n\", \"ioin\\n\\n\\n\\n\\n\", \"ho\\nnj\\n\", \"\\n\\nninh\\n\", \"ho\\nin\\n\", \"hzn\\nni\\n\", \"\\n\\n\\noni\\n\", \"hp\\nni\\n\", \"oi\\nin\\n\", \"hyoio\\n\\n\\n\\n\\n\", \"ohin\\n\\n\\n\", \"\\n\\n\\n\\nyoin\\n\", \"ohni\\n\", \"n\\nni\\n\", \"yh\\n\\nin\\n\", \"h\\nni\\n\", \"ni\\noi\\n\", \"yg\\n\\nin\\n\", \"g\\n\\n\\nypin\\n\", \"hxnho\\n\", \"\\n\\ngxpin\\n\", \"hn\\n\\nho\\n\", \"\\n\\ngpin\\n\", \"hyogn\\n\", \"hyn\\n\\ngn\\n\", \"\\n\\nqygin\\n\", \"n\\nfn\\n\", \"honihoni\\nhoni\"]}", "source": "taco"}
|
Emacs is a text editor which is widely used by many programmers.
The advantage of Emacs is that we can move a cursor without arrow keys and the mice. For example, the cursor can be moved right, left, down, and up by pushing f, b, n, p with the Control Key respectively. In addition, cut-and-paste can be performed without the mouse.
Your task is to write a program which simulates key operations in the Emacs-like editor. The program should read a text and print the corresponding edited text.
The text consists of several lines and each line consists of zero or more alphabets and space characters. A line, which does not have any character, is a blank line.
The editor has a cursor which can point out a character or the end-of-line in the corresponding line. The cursor can also point out the end-of-line in a blank line.
In addition, the editor has a buffer which can hold either a string (a sequence of characters) or a linefeed.
The editor accepts the following set of commands (If the corresponding line is a blank line, the word "the first character" should be "the end-of-line"):
* a
Move the cursor to the first character of the current line.
* e
Move the cursor to the end-of-line of the current line.
* p
Move the cursor to the first character of the next upper line, if it exists.
If there is no line above the current line, move the cursor to the first character of the current line.
* n
Move the cursor to the first character of the next lower line, if it exists.
If there is no line below the current line, move the cursor to the first character of the current line.
* f
Move the cursor by one character to the right, unless the cursor points out the end-of-line.
If the cursor points out the end-of-line and there is a line below the current line, move the cursor to the first character of the next lower line. Otherwise, do nothing.
* b
Move the cursor by one character to the left, unless the cursor points out the first character.
If the cursor points out the first character and there is a line above the current line, move the cursor to the end-of-line of the next upper line. Otherwise, do nothing.
* d
If the cursor points out a character, delete the character (Characters and end-of-line next to the deleted character are shifted to the left).
If the cursor points out the end-of-line and there is a line below, the next lower line is appended to the end-of-line of the current line (Lines below the current line are shifted to the upper).
Otherwise, do nothing.
* k
If the cursor points out the end-of-line and there is a line below the current line, perform the command d mentioned above, and record a linefeed on the buffer.
If the cursor does not point out the end-of-line, cut characters between the cursor (inclusive) and the end-of-line, and record them on the buffer. After this operation, the cursor indicates the end-of-line of the current line.
* y
If the buffer is empty, do nothing.
If the buffer is holding a linefeed, insert the linefeed at the cursor. The cursor moves to the first character of the new line.
If the buffer is holding characters, insert the characters at the cursor. The cursor moves to the character or end-of-line which is originally pointed by the cursor.
The cursor position just after reading the text is the beginning of the first line, and the initial buffer is empty.
Constraints
* The number of lines in the text given as input ≤ 10
* The number of characters in a line given as input ≤ 20
* The number of commands ≤ 300
* The maximum possible number of lines in the text during operations ≤ 100
* The maximum possible number of characters in a line during operations ≤ 1000
Input
The input consists of only one data-set which includes two parts. The first part gives a text consisting of several lines. The end of the text is indicated by a line (without quotes):
"END_OF_TEXT"
This line should not be included in the text.
Next part gives a series of commands. Each command is given in a line. The end of the commands is indicated by a character '-'.
Output
For the input text, print the text edited by the commands.
Example
Input
hyo
ni
END_OF_TEXT
f
d
f
f
k
p
p
e
y
a
k
y
y
n
y
-
Output
honihoni
honi
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"7 3\\nabb 2\\naaa -3\\nbba -1\\nzyz -4\\nabb 5\\naaa 7\\nxyx 4\\n\", \"3 1\\na 1\\na 2\\na 3\\n\", \"2 5\\nabcde 10000\\nabcde 10000\\n\", \"10 10\\nnjxbzflaka -1\\nfelbvvtkja 6\\ngxiuztqkcw 5\\naomvscmtti 6\\njsqmkoyuca -2\\nwckqtzuixg 5\\najktvvblef -5\\nittmcsvmoa -1\\nakalfzbxjn 10\\nacuyokmqsj 8\\n\", \"10 20\\njvyxocgomfmrtllgmagp 13\\ngvtjnyaofrswcnnifzfq 17\\nqisxpseggpjfoijmqnel -5\\nlenqmjiofjpggespxsiq 14\\nqfzfinncwsrfoaynjtvg 14\\ncaayidazlylxyisihdhx 14\\npgamglltrmfmogcoxyvj 11\\nxhdhisiyxlylzadiyaac 2\\ntbirihfpjgbbtclpxwhv 19\\nvhwxplctbbgjpfhiribt 10\\n\", \"1 1\\ne -1\\n\", \"2 1\\nt 1\\nt 2\\n\", \"1 2\\nyy 1\\n\", \"2 2\\nsn 1\\nns 2\\n\", \"3 3\\nada -1\\nxuv -1\\nvux 3\\n\", \"4 3\\ndbd 24\\naba 90\\ncbc 54\\naba 46\\n\", \"2 3\\naaa 5\\naaa -2\\n\", \"4 3\\naba 4\\naba 3\\naba 3\\naba -2\\n\", \"4 3\\naba 4\\naba 2\\naba 2\\naba -1\\n\", \"3 2\\naa 5\\naa -2\\nbb 1\\n\", \"2 2\\naa 500\\naa -50\\n\", \"2 1\\na 5\\na -1\\n\", \"2 3\\naba 10\\naba -3\\n\", \"2 3\\naba 10\\naba -9\\n\", \"10 10\\nnjxbzflaka -1\\nfelbvvtkja 6\\ngxiuztqkcw 5\\naomvscmtti 6\\njsqmkoyuca -2\\nwckqtzuixg 5\\najktvvblef -5\\nittmcsvmoa -1\\nakalfzbxjn 10\\nacuyokmqsj 8\\n\", \"3 3\\nada -1\\nxuv -1\\nvux 3\\n\", \"4 3\\ndbd 24\\naba 90\\ncbc 54\\naba 46\\n\", \"3 2\\naa 5\\naa -2\\nbb 1\\n\", \"2 2\\nsn 1\\nns 2\\n\", \"4 3\\naba 4\\naba 2\\naba 2\\naba -1\\n\", \"2 2\\naa 500\\naa -50\\n\", \"2 3\\naba 10\\naba -3\\n\", \"10 20\\njvyxocgomfmrtllgmagp 13\\ngvtjnyaofrswcnnifzfq 17\\nqisxpseggpjfoijmqnel -5\\nlenqmjiofjpggespxsiq 14\\nqfzfinncwsrfoaynjtvg 14\\ncaayidazlylxyisihdhx 14\\npgamglltrmfmogcoxyvj 11\\nxhdhisiyxlylzadiyaac 2\\ntbirihfpjgbbtclpxwhv 19\\nvhwxplctbbgjpfhiribt 10\\n\", \"2 1\\nt 1\\nt 2\\n\", \"1 2\\nyy 1\\n\", \"1 1\\ne -1\\n\", \"2 1\\na 5\\na -1\\n\", \"2 3\\naba 10\\naba -9\\n\", \"4 3\\naba 4\\naba 3\\naba 3\\naba -2\\n\", \"2 3\\naaa 5\\naaa -2\\n\", \"3 3\\nada -1\\nxuv -1\\nvux 6\\n\", \"4 3\\ndbd 24\\naba 90\\ncbc 54\\naca 46\\n\", \"2 2\\nsn 1\\nns 3\\n\", \"4 3\\naba 2\\naba 2\\naba 2\\naba -1\\n\", \"2 2\\naa 500\\naa -94\\n\", \"2 3\\naba 20\\naba -3\\n\", \"1 2\\nzy 1\\n\", \"4 3\\naba 4\\naba 3\\nabb 3\\naba -2\\n\", \"7 3\\nabb 2\\naaa -3\\nbba -2\\nzyz -4\\nabb 5\\naaa 7\\nxyx 4\\n\", \"2 2\\naa 821\\naa -94\\n\", \"2 2\\naa 77\\naa -94\\n\", \"2 3\\nabb 4\\naba 3\\nabb 3\\naba -2\\n\", \"2 2\\naa 113\\naa -94\\n\", \"3 2\\naa 5\\naa -2\\nbc 1\\n\", \"1 1\\nf -1\\n\", \"1 1\\na 5\\na -1\\n\", \"2 5\\ndbcae 10000\\nabcde 10000\\n\", \"3 1\\na 0\\na 2\\na 3\\n\", \"4 3\\ndbd 24\\naba 90\\ncbc 84\\naca 46\\n\", \"2 2\\nsn 1\\nsn 3\\n\", \"4 3\\naba 2\\naba 2\\naba 2\\naba -2\\n\", \"0 1\\nf -1\\n\", \"1 1\\na 5\\n` -1\\n\", \"2 3\\naba 4\\naba 3\\nabb 3\\naba -2\\n\", \"2 5\\ndbcae 10000\\nabcde 00000\\n\", \"4 3\\ndbd 24\\naba 90\\ncbc 20\\naca 46\\n\", \"2 2\\ntn 1\\nsn 3\\n\", \"4 3\\naba 2\\naba 2\\naab 2\\naba -2\\n\", \"0 1\\ne -1\\n\", \"1 1\\nb 5\\n` -1\\n\", \"2 5\\ndbdae 10000\\nabcde 00000\\n\", \"4 3\\ndbd 24\\naba 90\\ncbc 20\\naca 2\\n\", \"0 2\\ntn 1\\nsn 3\\n\", \"4 3\\naba 3\\naba 2\\naab 2\\naba -2\\n\", \"0 1\\ne -2\\n\", \"1 1\\nb 7\\n` -1\\n\", \"2 5\\neadbd 10000\\nabcde 00000\\n\", \"4 3\\ndbd 24\\naba 90\\ncbc 20\\naca 3\\n\", \"0 2\\ntn 1\\nns 3\\n\", \"2 2\\naa 113\\naa -120\\n\", \"0 1\\ne -3\\n\", \"2 5\\nebdbd 10000\\nabcde 00000\\n\", \"4 3\\nbdd 24\\naba 90\\ncbc 20\\naca 3\\n\", \"1 2\\naa 113\\naa -120\\n\", \"1 1\\ne -3\\n\", \"2 5\\nfbdbd 10000\\nabcde 00000\\n\", \"1 1\\ne -5\\n\", \"7 3\\nabb 2\\naaa -3\\nbba -1\\nzyz -4\\nabb 5\\naaa 7\\nxyx 4\\n\", \"2 5\\nabcde 10000\\nabcde 10000\\n\", \"3 1\\na 1\\na 2\\na 3\\n\"], \"outputs\": [\"12\\n\", \"6\\n\", \"0\\n\", \"31\\n\", \"109\\n\", \"0\\n\", \"3\\n\", \"1\\n\", \"3\\n\", \"2\\n\", \"190\\n\", \"5\\n\", \"10\\n\", \"8\\n\", \"5\\n\", \"500\\n\", \"5\\n\", \"10\\n\", \"10\\n\", \"31\\n\", \"2\\n\", \"190\\n\", \"5\\n\", \"3\\n\", \"8\\n\", \"500\\n\", \"10\\n\", \"109\\n\", \"3\\n\", \"1\\n\", \"0\\n\", \"5\\n\", \"10\\n\", \"10\\n\", \"5\\n\", \"5\\n\", \"90\\n\", \"4\\n\", \"6\\n\", \"500\\n\", \"20\\n\", \"0\\n\", \"7\\n\", \"11\\n\", \"821\\n\", \"77\\n\", \"3\\n\", \"113\\n\", \"5\\n\", \"0\\n\", \"5\\n\", \"0\\n\", \"5\\n\", \"90\\n\", \"0\\n\", \"6\\n\", \"0\\n\", \"5\\n\", \"7\\n\", \"0\\n\", \"90\\n\", \"0\\n\", \"4\\n\", \"0\\n\", \"5\\n\", \"0\\n\", \"90\\n\", \"0\\n\", \"5\\n\", \"0\\n\", \"7\\n\", \"0\\n\", \"90\\n\", \"0\\n\", \"113\\n\", \"0\\n\", \"0\\n\", \"90\\n\", \"113\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"12\\n\", \"0\\n\", \"6\\n\"]}", "source": "taco"}
|
Santa Claus likes palindromes very much. There was his birthday recently. k of his friends came to him to congratulate him, and each of them presented to him a string s_{i} having the same length n. We denote the beauty of the i-th string by a_{i}. It can happen that a_{i} is negative — that means that Santa doesn't find this string beautiful at all.
Santa Claus is crazy about palindromes. He is thinking about the following question: what is the maximum possible total beauty of a palindrome which can be obtained by concatenating some (possibly all) of the strings he has? Each present can be used at most once. Note that all strings have the same length n.
Recall that a palindrome is a string that doesn't change after one reverses it.
Since the empty string is a palindrome too, the answer can't be negative. Even if all a_{i}'s are negative, Santa can obtain the empty string.
-----Input-----
The first line contains two positive integers k and n divided by space and denoting the number of Santa friends and the length of every string they've presented, respectively (1 ≤ k, n ≤ 100 000; n·k ≤ 100 000).
k lines follow. The i-th of them contains the string s_{i} and its beauty a_{i} ( - 10 000 ≤ a_{i} ≤ 10 000). The string consists of n lowercase English letters, and its beauty is integer. Some of strings may coincide. Also, equal strings can have different beauties.
-----Output-----
In the only line print the required maximum possible beauty.
-----Examples-----
Input
7 3
abb 2
aaa -3
bba -1
zyz -4
abb 5
aaa 7
xyx 4
Output
12
Input
3 1
a 1
a 2
a 3
Output
6
Input
2 5
abcde 10000
abcde 10000
Output
0
-----Note-----
In the first example Santa can obtain abbaaaxyxaaabba by concatenating strings 5, 2, 7, 6 and 3 (in this order).
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4 10\\n3 4 3 3\\n2\\n4 3\\n\", \"5 9\\n4 4 2 3 2\\n5\\n1 4 2 3 5\\n\", \"6 15\\n4 3 5 4 2 1\\n6\\n1 2 3 4 5 6\\n\", \"5 9\\n4 4 2 3 4\\n5\\n1 4 2 3 5\", \"6 15\\n4 3 5 4 2 1\\n6\\n1 2 3 0 5 6\", \"6 15\\n4 3 5 4 2 1\\n6\\n1 2 4 0 5 6\", \"6 15\\n4 3 5 4 0 1\\n6\\n1 2 3 4 5 6\", \"4 10\\n3 2 3 3\\n2\\n4 3\", \"6 15\\n4 3 5 4 2 1\\n6\\n1 3 3 0 5 6\", \"6 15\\n4 3 5 4 0 1\\n6\\n2 2 4 0 5 6\", \"6 15\\n4 3 5 3 0 1\\n6\\n0 2 4 0 5 6\", \"6 15\\n4 1 5 4 2 1\\n6\\n1 2 3 4 5 6\", \"6 15\\n4 3 5 4 0 1\\n6\\n1 2 1 4 4 6\", \"6 15\\n4 2 5 4 0 1\\n6\\n2 2 1 4 5 6\", \"6 15\\n4 3 5 3 0 0\\n6\\n1 2 4 0 5 6\", \"6 15\\n4 4 5 4 2 1\\n6\\n1 2 3 4 5 6\", \"6 15\\n4 3 5 4 0 1\\n6\\n0 2 3 4 5 6\", \"5 9\\n4 2 0 3 4\\n5\\n1 4 2 2 5\", \"6 15\\n4 3 5 4 0 1\\n6\\n2 0 4 0 5 6\", \"6 15\\n4 3 5 8 2 1\\n6\\n1 3 3 0 5 5\", \"6 15\\n4 3 5 4 0 1\\n6\\n1 2 0 4 4 6\", \"6 9\\n4 3 5 1 0 1\\n6\\n1 1 3 4 5 6\", \"6 15\\n4 3 5 4 0 1\\n6\\n1 0 0 4 4 6\", \"6 15\\n2 8 5 4 2 1\\n6\\n1 2 3 4 5 6\", \"5 9\\n4 2 0 3 7\\n5\\n0 4 2 2 5\", \"6 5\\n4 2 5 3 0 1\\n6\\n0 2 4 0 6 6\", \"6 9\\n4 3 8 1 0 1\\n6\\n1 1 3 4 5 6\", \"6 15\\n4 5 10 4 2 1\\n6\\n1 3 3 0 5 6\", \"6 9\\n4 3 8 1 0 1\\n6\\n0 1 3 4 5 6\", \"5 8\\n4 7 3 0 0\\n5\\n2 4 2 3 4\", \"5 8\\n4 7 3 1 0\\n5\\n2 4 2 3 4\", \"5 8\\n2 7 3 1 0\\n5\\n2 4 2 3 4\", \"6 15\\n1 8 5 2 0 1\\n6\\n1 2 3 4 2 6\", \"6 15\\n2 8 5 2 0 1\\n6\\n1 2 3 1 2 6\", \"6 15\\n4 3 5 4 0 1\\n6\\n2 2 5 0 5 6\", \"6 15\\n8 3 5 4 0 1\\n6\\n0 3 4 0 5 6\", \"6 15\\n4 0 5 4 2 1\\n6\\n1 2 3 4 5 6\", \"6 15\\n4 8 5 8 2 1\\n6\\n1 2 3 4 5 6\", \"5 9\\n7 2 0 3 7\\n5\\n0 4 2 2 5\", \"6 5\\n4 2 5 3 0 1\\n6\\n0 2 6 0 6 6\", \"6 9\\n4 3 8 1 0 1\\n6\\n0 1 3 4 5 5\", \"5 6\\n4 7 3 1 0\\n5\\n2 4 2 3 4\", \"5 1\\n2 7 3 1 0\\n5\\n2 4 2 3 4\", \"5 9\\n4 4 4 3 1\\n5\\n1 4 2 3 5\", \"6 15\\n4 3 8 4 2 1\\n6\\n1 2 3 2 5 6\", \"6 15\\n4 3 5 4 1 1\\n6\\n1 2 5 4 5 6\", \"5 3\\n4 1 2 3 4\\n5\\n1 4 2 3 5\", \"6 15\\n4 0 5 4 2 0\\n6\\n1 2 3 4 5 6\", \"6 15\\n4 4 5 0 2 1\\n6\\n1 2 1 4 5 6\", \"6 9\\n4 3 5 1 0 1\\n6\\n0 1 5 4 5 1\", \"5 6\\n4 7 3 1 0\\n5\\n2 4 3 3 4\", \"5 1\\n2 7 3 1 0\\n5\\n4 4 2 3 4\", \"6 15\\n4 3 5 5 1 1\\n6\\n1 2 5 4 5 6\", \"6 15\\n4 3 2 5 2 1\\n6\\n1 3 1 0 4 6\", \"5 6\\n6 7 3 1 0\\n5\\n2 4 3 3 4\", \"6 15\\n1 8 5 2 1 2\\n6\\n1 2 3 5 2 6\", \"6 15\\n4 3 5 5 1 1\\n6\\n1 2 5 4 5 1\", \"6 17\\n4 3 5 4 3 1\\n6\\n1 1 2 0 6 6\", \"5 4\\n4 2 2 4 8\\n5\\n1 4 2 1 1\", \"6 2\\n4 3 5 4 0 1\\n6\\n2 0 4 0 5 6\", \"6 15\\n4 3 5 4 1 1\\n6\\n1 0 0 4 4 6\", \"6 15\\n4 0 5 4 2 1\\n6\\n1 2 3 2 5 6\", \"5 9\\n4 2 0 3 4\\n5\\n1 5 2 2 2\", \"5 9\\n4 4 4 4 1\\n5\\n1 4 2 3 5\", \"6 2\\n2 3 4 9 2 0\\n6\\n1 4 3 0 5 6\", \"6 15\\n2 8 5 7 0 1\\n6\\n1 2 5 4 5 6\", \"6 10\\n1 8 5 1 0 2\\n6\\n1 2 3 4 2 6\", \"6 15\\n4 0 5 4 2 0\\n6\\n0 2 3 4 6 6\", \"5 4\\n4 2 2 5 8\\n5\\n1 4 2 0 1\", \"5 4\\n4 2 2 5 12\\n5\\n1 4 2 1 0\", \"5 8\\n4 4 2 3 2\\n5\\n1 2 2 3 5\", \"6 15\\n4 0 5 3 2 1\\n6\\n1 2 3 4 5 6\", \"4 1\\n1 4 1 3\\n2\\n4 3\", \"5 4\\n4 4 2 3 2\\n5\\n1 4 2 3 5\", \"4 1\\n0 4 1 3\\n2\\n4 3\", \"5 12\\n4 4 4 0 2\\n5\\n1 2 5 3 0\", \"6 11\\n4 0 5 12 2 1\\n6\\n2 2 3 4 5 6\", \"6 11\\n4 0 5 3 4 1\\n6\\n2 2 3 4 5 6\", \"5 8\\n4 4 2 3 0\\n5\\n0 4 2 3 5\", \"4 16\\n3 7 3 3\\n2\\n4 0\", \"6 15\\n4 0 7 4 2 1\\n6\\n1 0 1 5 2 6\", \"5 8\\n4 0 4 3 0\\n5\\n0 2 2 5 5\", \"6 15\\n7 3 9 1 2 1\\n6\\n1 3 3 4 5 6\", \"6 12\\n4 0 5 12 2 1\\n6\\n0 2 0 3 5 6\", \"6 15\\n4 3 4 4 2 1\\n6\\n1 2 3 4 5 6\", \"6 11\\n4 0 1 4 2 1\\n6\\n2 2 3 4 5 6\", \"6 15\\n4 0 5 4 2 1\\n6\\n1 2 6 2 5 6\", \"6 11\\n4 1 5 4 1 0\\n6\\n1 2 4 4 5 6\", \"6 15\\n6 1 5 4 2 1\\n6\\n1 2 2 4 1 6\", \"5 8\\n5 4 1 3 0\\n5\\n2 2 4 3 2\", \"5 8\\n5 4 1 3 0\\n5\\n4 0 2 3 2\", \"6 15\\n4 0 5 4 2 1\\n6\\n2 4 0 4 5 6\", \"5 9\\n4 2 2 3 4\\n5\\n1 4 2 3 5\", \"6 15\\n4 3 5 4 0 1\\n6\\n1 2 1 4 5 6\", \"5 9\\n4 2 2 3 4\\n5\\n1 4 2 2 5\", \"6 15\\n4 3 5 4 0 1\\n6\\n2 2 1 4 5 6\", \"6 15\\n4 3 5 4 0 1\\n6\\n2 2 2 4 5 6\", \"6 15\\n4 3 5 4 0 1\\n6\\n2 2 4 4 5 6\", \"6 15\\n4 3 5 4 0 1\\n6\\n0 2 4 0 5 6\", \"6 15\\n4 3 5 3 0 0\\n6\\n0 2 4 0 5 6\", \"4 10\\n3 1 3 3\\n2\\n4 3\", \"5 9\\n4 4 2 3 4\\n5\\n1 4 1 3 5\", \"6 15\\n4 3 5 4 4 1\\n6\\n1 2 4 0 5 6\", \"5 9\\n4 4 2 3 2\\n5\\n1 4 2 3 5\", \"6 15\\n4 3 5 4 2 1\\n6\\n1 2 3 4 5 6\", \"4 10\\n3 4 3 3\\n2\\n4 3\"], \"outputs\": [\"NO\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nYES\\n\", \"NO\\nNO\\nYES\\nNO\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nYES\\n\", \"NO\\nNO\\nYES\\nNO\\nNO\\nYES\\n\", \"NO\\nNO\\nNO\\nNO\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nNO\\nYES\\n\", \"YES\\nYES\\n\", \"NO\\nYES\\nYES\\nNO\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nNO\\nNO\\nYES\\n\", \"NO\\nYES\\nYES\\nNO\\nNO\\nNO\\n\", \"YES\\nNO\\nYES\\nYES\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nYES\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nNO\\nNO\\n\", \"YES\\nYES\\nYES\\nNO\\nNO\\nNO\\n\", \"NO\\nNO\\nNO\\nNO\\nYES\\nNO\\n\", \"NO\\nYES\\nYES\\nYES\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nNO\\n\", \"YES\\nNO\\nYES\\nNO\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nNO\\nYES\\nYES\\n\", \"YES\\nYES\\nNO\\nYES\\nYES\\nYES\\n\", \"NO\\nNO\\nNO\\nYES\\nNO\\nYES\\n\", \"YES\\nNO\\nNO\\nYES\\nYES\\nYES\\n\", \"NO\\nYES\\nNO\\nNO\\nNO\\nNO\\n\", \"NO\\nYES\\nYES\\nYES\\nNO\\n\", \"NO\\nNO\\nNO\\nNO\\nYES\\nYES\\n\", \"YES\\nYES\\nNO\\nYES\\nNO\\nYES\\n\", \"NO\\nNO\\nNO\\nNO\\nNO\\nNO\\n\", \"NO\\nYES\\nNO\\nYES\\nNO\\nYES\\n\", \"YES\\nNO\\nYES\\nYES\\nNO\\n\", \"NO\\nNO\\nNO\\nYES\\nNO\\n\", \"YES\\nYES\\nYES\\nNO\\nYES\\n\", \"NO\\nYES\\nYES\\nNO\\nYES\\nYES\\n\", \"NO\\nYES\\nYES\\nNO\\nYES\\nNO\\n\", \"YES\\nYES\\nNO\\nNO\\nNO\\nYES\\n\", \"NO\\nYES\\nNO\\nNO\\nNO\\nYES\\n\", \"YES\\nNO\\nYES\\nYES\\nYES\\nNO\\n\", \"NO\\nYES\\nNO\\nNO\\nYES\\nNO\\n\", \"NO\\nNO\\nYES\\nYES\\nNO\\n\", \"NO\\nNO\\nYES\\nNO\\nYES\\nYES\\n\", \"NO\\nYES\\nNO\\nYES\\nNO\\nNO\\n\", \"NO\\nYES\\nNO\\nYES\\nYES\\n\", \"NO\\nYES\\nNO\\nNO\\nYES\\n\", \"NO\\nNO\\nNO\\nNO\\nYES\\n\", \"NO\\nNO\\nYES\\nNO\\nNO\\nNO\\n\", \"YES\\nNO\\nNO\\nYES\\nNO\\nNO\\n\", \"YES\\nNO\\nYES\\nNO\\nNO\\n\", \"YES\\nYES\\nYES\\nYES\\nYES\\nNO\\n\", \"YES\\nYES\\nYES\\nNO\\nYES\\nNO\\n\", \"NO\\nNO\\nNO\\nYES\\nNO\\nNO\\n\", \"NO\\nYES\\nYES\\nYES\\nYES\\n\", \"YES\\nYES\\nNO\\nNO\\nYES\\n\", \"NO\\nNO\\nYES\\nYES\\nYES\\nYES\\n\", \"YES\\nNO\\nYES\\nNO\\nYES\\nYES\\n\", \"NO\\nNO\\nNO\\nNO\\nNO\\n\", \"NO\\nYES\\nYES\\nYES\\nYES\\nNO\\n\", \"NO\\nNO\\nYES\\nYES\\nYES\\nNO\\n\", \"YES\\nYES\\nNO\\nNO\\nYES\\nYES\\n\", \"YES\\nNO\\nNO\\nYES\\nYES\\n\", \"YES\\nNO\\nNO\\nNO\\nNO\\nYES\\n\", \"YES\\nNO\\nNO\\nYES\\nYES\\nNO\\n\", \"YES\\nNO\\nYES\\nNO\\nYES\\nNO\\n\", \"YES\\nNO\\nYES\\nYES\\nYES\\n\", \"YES\\nNO\\nYES\\nNO\\nYES\\n\", \"YES\\nNO\\nNO\\nNO\\nNO\\nNO\\n\", \"YES\\nYES\\nNO\\nNO\\nNO\\nNO\\n\", \"YES\\nYES\\nNO\\nYES\\nYES\\nNO\\n\", \"NO\\nYES\\nYES\\nYES\\nNO\\nNO\\n\", \"YES\\nNO\\nNO\\nNO\\nYES\\n\", \"YES\\nNO\\nNO\\nYES\\nNO\\n\", \"YES\\nYES\\nYES\\nNO\\nNO\\n\", \"YES\\nNO\\nYES\\nYES\\nYES\\nYES\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\nNO\\nNO\\nNO\\n\", \"NO\\nYES\\n\", \"YES\\nYES\\nNO\\nYES\\nNO\\n\", \"NO\\nNO\\nYES\\nNO\\nYES\\nNO\\n\", \"NO\\nNO\\nYES\\nYES\\nNO\\nYES\\n\", \"NO\\nNO\\nYES\\nNO\\nNO\\n\", \"YES\\nNO\\n\", \"YES\\nNO\\nYES\\nNO\\nNO\\nNO\\n\", \"NO\\nYES\\nYES\\nNO\\nNO\\n\", \"NO\\nYES\\nYES\\nYES\\nYES\\nYES\\n\", \"NO\\nNO\\nNO\\nYES\\nYES\\nYES\\n\", \"YES\\nNO\\nYES\\nYES\\nNO\\nNO\\n\", \"NO\\nNO\\nNO\\nYES\\nYES\\nNO\\n\", \"YES\\nNO\\nNO\\nNO\\nYES\\nNO\\n\", \"YES\\nYES\\nNO\\nNO\\nYES\\nNO\\n\", \"YES\\nNO\\nNO\\nNO\\nYES\\nYES\\n\", \"YES\\nYES\\nNO\\nYES\\nYES\\n\", \"NO\\nNO\\nYES\\nYES\\nYES\\n\", \"NO\\nYES\\nNO\\nYES\\nYES\\nNO\\n\", \"YES\\nYES\\nYES\\nYES\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nNO\\nYES\\n\", \"NO\\nYES\\nYES\\nNO\\nNO\\nYES\\n\", \"NO\\nYES\\nYES\\nNO\\nNO\\nNO\\n\", \"YES\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nYES\\n\", \"YES\\nYES\\nYES\\nNO\\nNO\\nYES\\n\", \"YES\\nYES\\nYES\\nYES\\nYES\", \"NO\\nNO\\nYES\\nNO\\nNO\\nYES\", \"NO\\nYES\"]}", "source": "taco"}
|
Alice lives on a line. Today, she will travel to some place in a mysterious vehicle.
Initially, the distance between Alice and her destination is D. When she input a number x to the vehicle, it will travel in the direction of the destination by a distance of x if this move would shorten the distance between the vehicle and the destination, and it will stay at its position otherwise. Note that the vehicle may go past the destination when the distance between the vehicle and the destination is less than x.
Alice made a list of N numbers. The i-th number in this list is d_i. She will insert these numbers to the vehicle one by one.
However, a mischievous witch appeared. She is thinking of rewriting one number in the list so that Alice will not reach the destination after N moves.
She has Q plans to do this, as follows:
- Rewrite only the q_i-th number in the list with some integer so that Alice will not reach the destination.
Write a program to determine whether each plan is feasible.
-----Constraints-----
- 1≤ N ≤ 5*10^5
- 1≤ Q ≤ 5*10^5
- 1≤ D ≤ 10^9
- 1≤ d_i ≤ 10^9(1≤i≤N)
- 1≤ q_i ≤ N(1≤i≤Q)
- D and each d_i are integers.
-----Input-----
Input is given from Standard Input in the following format:
N D
d_1 d_2 ... d_N
Q
q_1 q_2 ... q_Q
-----Output-----
Print Q lines. The i-th line should contain YES if the i-th plan is feasible, and NO otherwise.
-----Sample Input-----
4 10
3 4 3 3
2
4 3
-----Sample Output-----
NO
YES
For the first plan, Alice will already arrive at the destination by the first three moves, and therefore the answer is NO.
For the second plan, rewriting the third number in the list with 5 will prevent Alice from reaching the destination as shown in the following figure, and thus the answer is YES.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 2 3 8 5\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 2 3 8 3\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 2 1 8 5\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 2 3 2 3\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 0 3 2 6\\n3 1 2 1 4 3 1 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n17\\n2 3 1 8 2\\n5 1 3 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 2 3 3 5\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 2\\n0\\n17\\n2 2 1 8 5\\n3 1 4 1 4 2 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 0 8 5\\n0\\n10\\n2 0 3 2 3\\n3 1 2 1 4 3 1 9 1 1\", \"3\\n10\\n2 1 3 8 2\\n0\\n10\\n2 1 3 8 5\\n0\\n17\\n2 2 1 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 3 8 2\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 2 3 3 5\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 0 3 8 1\\n0\\n10\\n2 1 3 8 9\\n0\\n10\\n2 2 3 8 3\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n17\\n2 2 1 8 5\\n5 1 2 1 4 3 3 9 1 1\", \"3\\n10\\n2 1 3 8 2\\n0\\n10\\n2 1 3 8 9\\n0\\n17\\n2 2 1 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 4 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 0 3 2 6\\n3 1 2 1 4 3 1 10 1 0\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 1\\n0\\n6\\n2 3 1 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 4 8 5\\n0\\n17\\n2 3 1 8 2\\n5 0 3 1 4 1 2 9 1 0\", \"3\\n16\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 -1 3 2 4\\n3 1 3 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 16 1\\n0\\n8\\n2 1 0 8 10\\n0\\n10\\n2 2 3 3 3\\n6 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 0 16 1\\n0\\n8\\n2 1 0 8 10\\n0\\n10\\n2 2 3 3 3\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 1 0 1\\n0\\n0\\n2 1 3 8 5\\n0\\n18\\n2 2 0 8 5\\n3 1 12 1 4 3 2 11 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 6 8 5\\n0\\n10\\n2 2 3 2 3\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 1 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 0 3 2 3\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 5 8 5\\n0\\n10\\n2 0 3 3 6\\n3 1 2 1 4 3 1 9 1 1\", \"3\\n10\\n2 1 3 8 2\\n0\\n10\\n2 1 3 8 10\\n0\\n17\\n2 2 1 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 4\\n0\\n17\\n2 3 1 8 5\\n5 1 3 1 4 1 2 13 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 6 8 5\\n0\\n17\\n2 3 1 8 2\\n5 1 3 1 4 1 2 9 1 0\", \"3\\n10\\n2 1 3 8 2\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 2 3 3 9\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 2\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 2 2 3 5\\n3 1 2 1 5 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 1\\n0\\n6\\n2 3 2 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 4 8 5\\n0\\n17\\n2 3 1 3 2\\n5 0 3 1 4 1 2 9 1 0\", \"3\\n10\\n2 1 4 16 1\\n0\\n8\\n2 1 0 8 10\\n0\\n10\\n2 2 3 3 3\\n6 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 2\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 0 3 2 11\\n3 1 2 1 4 3 1 14 1 0\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 0\\n0\\n17\\n2 2 1 8 3\\n5 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 4\\n0\\n17\\n2 3 2 8 5\\n5 1 3 1 4 1 2 13 1 1\", \"3\\n10\\n2 1 3 8 0\\n0\\n10\\n2 1 6 8 5\\n0\\n17\\n2 3 1 8 2\\n5 1 3 1 4 1 2 9 1 0\", \"3\\n10\\n2 0 3 8 1\\n0\\n10\\n2 0 3 8 9\\n0\\n10\\n2 2 3 8 3\\n3 1 2 0 4 3 2 9 1 1\", \"3\\n10\\n2 1 4 8 1\\n0\\n10\\n2 1 6 8 5\\n0\\n6\\n2 3 1 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n15\\n2 1 3 16 1\\n0\\n8\\n2 1 0 8 5\\n0\\n10\\n2 2 3 3 3\\n6 1 2 2 4 3 2 9 1 1\", \"3\\n16\\n2 1 3 8 1\\n0\\n10\\n2 1 4 8 5\\n0\\n10\\n2 -1 3 1 4\\n3 0 3 0 4 3 3 9 1 1\", \"3\\n15\\n2 1 3 0 0\\n0\\n10\\n2 1 3 7 5\\n0\\n10\\n2 -1 3 2 2\\n3 0 3 0 2 3 1 9 1 1\", \"3\\n10\\n2 2 3 8 1\\n0\\n10\\n2 1 6 8 5\\n0\\n10\\n2 2 3 2 6\\n3 1 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 6 8 1\\n0\\n10\\n2 1 3 8 1\\n0\\n6\\n2 3 2 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 4 16 1\\n0\\n8\\n2 1 0 8 10\\n0\\n10\\n2 2 2 3 3\\n6 2 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 16 1\\n0\\n8\\n2 1 0 8 10\\n0\\n10\\n2 2 3 3 3\\n3 1 2 1 1 2 2 9 1 0\", \"3\\n16\\n2 1 3 8 1\\n0\\n10\\n2 1 4 8 5\\n0\\n10\\n2 -1 3 1 4\\n3 0 3 0 1 3 3 9 1 1\", \"3\\n10\\n2 1 1 0 1\\n0\\n-1\\n2 1 3 8 5\\n0\\n18\\n2 2 0 8 5\\n3 2 12 1 4 3 3 11 1 1\", \"3\\n10\\n2 0 3 8 1\\n0\\n10\\n2 0 3 8 10\\n0\\n10\\n2 2 3 8 0\\n3 1 2 1 4 3 2 3 1 1\", \"3\\n10\\n2 1 1 8 2\\n0\\n10\\n2 0 3 8 5\\n0\\n10\\n2 2 3 3 9\\n3 1 2 1 4 5 2 9 1 1\", \"3\\n10\\n2 0 6 8 1\\n-1\\n10\\n2 0 3 8 9\\n0\\n10\\n2 2 3 8 3\\n3 1 2 0 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 2\\n-1\\n7\\n2 1 3 8 9\\n0\\n17\\n2 2 1 8 5\\n3 1 4 0 4 1 2 9 1 2\", \"3\\n10\\n2 1 4 3 2\\n0\\n10\\n2 1 6 8 5\\n0\\n6\\n2 3 1 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 3 16 2\\n0\\n8\\n2 1 0 8 10\\n0\\n10\\n2 2 3 3 3\\n3 1 2 1 1 2 2 9 1 0\", \"3\\n10\\n2 1 5 0 1\\n0\\n0\\n2 1 3 8 5\\n0\\n17\\n2 2 0 8 8\\n3 0 4 1 4 3 2 11 1 1\", \"3\\n10\\n2 0 3 8 1\\n0\\n10\\n2 0 3 8 10\\n0\\n10\\n2 2 3 8 0\\n3 1 2 2 4 3 2 3 1 1\", \"3\\n4\\n2 1 3 0 1\\n0\\n10\\n2 1 5 8 5\\n0\\n17\\n2 2 1 3 5\\n3 1 4 2 6 2 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 6 8 5\\n0\\n17\\n2 3 1 8 4\\n5 2 3 1 4 1 2 9 1 0\", \"3\\n10\\n2 1 1 8 0\\n0\\n10\\n2 0 3 8 5\\n0\\n10\\n2 2 3 3 9\\n3 1 2 1 4 5 2 9 1 1\", \"3\\n10\\n2 1 4 3 2\\n0\\n10\\n2 1 6 8 5\\n0\\n6\\n2 0 1 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 4\\n0\\n17\\n2 3 1 8 2\\n5 0 4 1 2 1 2 24 1 0\", \"3\\n10\\n2 1 4 16 2\\n0\\n12\\n2 1 0 8 10\\n0\\n10\\n2 2 2 3 3\\n6 2 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 1 0 1\\n0\\n0\\n2 1 3 8 2\\n0\\n18\\n2 2 0 8 5\\n3 2 12 1 4 3 3 11 1 1\", \"3\\n10\\n2 1 1 8 1\\n0\\n10\\n2 1 6 8 5\\n0\\n17\\n2 3 1 8 4\\n5 2 3 1 4 1 2 9 1 0\", \"3\\n15\\n2 1 3 0 1\\n0\\n10\\n2 1 3 8 0\\n0\\n20\\n2 2 1 13 5\\n3 1 6 0 4 2 2 13 1 1\", \"3\\n10\\n2 1 3 8 2\\n-1\\n7\\n2 1 3 8 9\\n-1\\n17\\n2 2 1 8 5\\n3 1 4 0 4 1 0 9 1 2\", \"3\\n14\\n2 0 6 8 1\\n-1\\n8\\n2 0 3 8 6\\n0\\n10\\n2 2 3 8 3\\n3 1 2 0 4 3 2 9 1 1\", \"3\\n10\\n2 1 3 8 2\\n-1\\n7\\n2 1 1 8 9\\n-1\\n17\\n2 2 1 8 5\\n3 1 4 0 4 1 0 9 1 2\", \"3\\n10\\n2 2 0 3 1\\n0\\n8\\n2 1 3 8 5\\n0\\n10\\n2 2 4 2 2\\n6 1 2 1 4 3 0 9 1 1\", \"3\\n20\\n2 1 3 0 0\\n0\\n0\\n2 1 3 8 5\\n-1\\n22\\n2 2 1 8 5\\n3 1 6 0 4 1 2 9 1 1\", \"3\\n12\\n2 1 0 4 2\\n0\\n10\\n2 1 3 8 9\\n0\\n6\\n2 2 1 8 5\\n6 1 3 1 4 1 2 9 1 1\", \"3\\n10\\n2 1 4 16 2\\n0\\n12\\n2 1 0 8 17\\n0\\n10\\n2 2 2 3 3\\n10 2 2 1 4 3 2 9 1 1\", \"3\\n10\\n2 1 6 0 1\\n0\\n0\\n2 1 3 8 5\\n0\\n17\\n2 2 0 8 8\\n3 0 6 2 4 3 2 11 1 1\", \"3\\n10\\n2 1 1 8 1\\n-1\\n10\\n2 1 1 8 5\\n0\\n17\\n2 3 1 8 4\\n5 2 3 1 4 1 2 9 1 0\", \"3\\n10\\n2 1 1 8 0\\n0\\n10\\n2 0 3 8 5\\n0\\n10\\n2 1 4 3 9\\n3 1 2 1 5 5 2 9 1 1\", \"3\\n10\\n2 0 2 3 2\\n0\\n4\\n2 1 6 8 5\\n0\\n6\\n2 0 1 8 5\\n3 1 4 1 4 1 2 9 1 1\", \"3\\n10\\n2 2 0 3 1\\n0\\n8\\n2 1 3 8 5\\n0\\n10\\n2 2 4 2 1\\n6 1 2 1 4 3 0 9 1 1\", \"3\\n10\\n2 1 4 0 1\\n0\\n0\\n2 1 3 8 5\\n0\\n17\\n2 2 0 8 8\\n3 0 6 2 4 3 2 11 1 1\", \"3\\n10\\n2 2 3 8 1\\n0\\n10\\n2 1 3 8 4\\n0\\n10\\n2 2 1 15 10\\n3 1 3 1 3 1 1 9 1 1\", \"3\\n10\\n2 1 2 8 1\\n-1\\n10\\n2 1 1 8 5\\n0\\n17\\n2 3 1 8 4\\n5 2 3 1 4 1 2 9 1 0\", \"3\\n10\\n2 1 3 8 1\\n0\\n1\\n2 1 3 8 1\\n-1\\n6\\n2 3 2 8 5\\n3 2 4 0 4 2 0 4 1 1\", \"3\\n10\\n2 2 3 8 2\\n0\\n10\\n2 1 3 8 4\\n0\\n10\\n2 2 1 15 10\\n3 1 3 1 3 1 1 9 1 1\", \"3\\n10\\n2 1 3 1 1\\n0\\n10\\n2 2 3 8 4\\n0\\n17\\n2 3 1 8 2\\n5 0 6 1 2 1 1 24 0 0\", \"3\\n10\\n2 2 3 8 2\\n0\\n10\\n2 1 3 8 4\\n0\\n10\\n2 2 1 15 10\\n3 1 3 1 3 1 1 9 1 0\", \"3\\n10\\n2 1 3 8 1\\n0\\n8\\n2 1 3 3 0\\n0\\n17\\n2 3 1 8 2\\n5 0 0 1 6 2 2 23 0 0\", \"3\\n10\\n2 1 1 8 0\\n0\\n10\\n2 0 3 13 7\\n0\\n10\\n2 1 4 3 9\\n3 0 2 1 5 5 2 9 1 1\", \"3\\n10\\n2 1 3 -1 2\\n0\\n0\\n2 1 3 7 5\\n0\\n6\\n1 2 1 12 0\\n3 0 6 1 4 1 2 11 1 0\", \"3\\n10\\n2 1 4 16 2\\n0\\n10\\n2 1 0 8 11\\n0\\n10\\n2 2 2 3 4\\n10 2 2 1 4 3 2 9 1 0\", \"3\\n10\\n2 2 3 8 2\\n0\\n10\\n2 1 0 8 4\\n0\\n10\\n2 2 1 15 10\\n3 1 3 1 3 1 1 9 1 0\", \"3\\n10\\n2 1 1 8 0\\n0\\n10\\n2 0 3 13 7\\n0\\n10\\n2 1 4 3 15\\n3 0 2 1 5 5 2 9 1 1\", \"3\\n10\\n2 2 3 8 2\\n0\\n10\\n2 1 -1 8 4\\n0\\n10\\n2 2 1 15 10\\n3 1 3 1 3 1 1 9 1 0\", \"3\\n10\\n2 1 1 8 0\\n0\\n10\\n2 0 3 13 7\\n0\\n10\\n2 1 6 3 15\\n3 0 2 1 5 5 2 9 1 1\", \"3\\n10\\n2 1 3 -1 2\\n0\\n0\\n2 1 1 7 5\\n0\\n6\\n2 2 1 12 0\\n3 0 6 1 4 1 2 11 1 0\", \"3\\n10\\n2 1 8 8 1\\n-1\\n30\\n2 1 3 13 5\\n0\\n10\\n2 0 2 3 6\\n8 1 2 1 7 3 1 10 1 1\", \"3\\n10\\n2 1 4 16 2\\n0\\n10\\n2 1 0 8 9\\n0\\n10\\n2 2 2 3 2\\n10 2 2 1 4 3 2 9 1 0\", \"3\\n10\\n2 2 3 8 2\\n0\\n10\\n2 1 -1 8 4\\n0\\n10\\n2 2 1 15 15\\n3 1 3 1 3 1 1 9 1 0\", \"3\\n4\\n2 2 3 0 1\\n0\\n8\\n2 1 7 8 2\\n-1\\n17\\n2 2 1 3 5\\n4 1 4 4 6 2 2 18 0 1\", \"3\\n10\\n2 1 1 8 0\\n0\\n10\\n2 0 3 13 7\\n0\\n10\\n2 1 6 3 15\\n3 0 2 2 5 5 2 9 1 1\", \"3\\n10\\n2 1 8 8 1\\n-1\\n30\\n2 1 3 13 7\\n0\\n4\\n2 0 2 3 6\\n8 1 2 1 7 3 1 10 1 1\", \"3\\n10\\n2 1 3 -1 2\\n0\\n-1\\n2 1 2 7 5\\n0\\n9\\n2 2 1 12 0\\n3 0 6 1 4 1 2 18 1 0\", \"3\\n10\\n2 2 3 4 2\\n0\\n10\\n2 0 -2 8 4\\n0\\n10\\n2 3 1 15 15\\n3 1 2 1 3 1 1 9 1 0\", \"3\\n10\\n2 2 3 4 2\\n0\\n10\\n2 0 -2 8 4\\n0\\n10\\n2 3 1 15 15\\n3 1 2 0 3 1 1 9 1 0\", \"3\\n10\\n2 1 3 8 1\\n0\\n10\\n2 1 3 8 5\\n0\\n10\\n2 2 3 8 5\\n3 1 2 1 4 3 2 9 1 1\"], \"outputs\": [\"5\\n9\\n6\", \"5\\n9\\n5\\n\", \"5\\n9\\n4\\n\", \"5\\n9\\n6\\n\", \"5\\n9\\n9\\n\", \"5\\n9\\n2\\n\", \"5\\n9\\n8\\n\", \"5\\n6\\n4\\n\", \"5\\n6\\n6\\n\", \"6\\n9\\n4\\n\", \"6\\n9\\n8\\n\", \"5\\n13\\n5\\n\", \"5\\n9\\n3\\n\", \"6\\n13\\n4\\n\", \"6\\n9\\n9\\n\", \"5\\n5\\n4\\n\", \"5\\n10\\n2\\n\", \"5\\n9\\n7\\n\", \"5\\n11\\n6\\n\", \"2\\n11\\n6\\n\", \"3\\n9\\n4\\n\", \"5\\n12\\n6\\n\", \"3\\n9\\n6\\n\", \"5\\n11\\n9\\n\", \"6\\n14\\n4\\n\", \"5\\n8\\n4\\n\", \"5\\n12\\n2\\n\", \"6\\n9\\n12\\n\", \"6\\n9\\n7\\n\", \"5\\n5\\n5\\n\", \"5\\n10\\n3\\n\", \"6\\n11\\n6\\n\", \"6\\n9\\n14\\n\", \"5\\n4\\n3\\n\", \"5\\n8\\n5\\n\", \"4\\n12\\n2\\n\", \"5\\n13\\n6\\n\", \"6\\n12\\n4\\n\", \"5\\n6\\n5\\n\", \"5\\n10\\n8\\n\", \"4\\n9\\n6\\n\", \"5\\n12\\n9\\n\", \"8\\n5\\n5\\n\", \"6\\n11\\n5\\n\", \"5\\n11\\n4\\n\", \"5\\n10\\n6\\n\", \"3\\n9\\n3\\n\", \"5\\n14\\n3\\n\", \"4\\n9\\n12\\n\", \"8\\n13\\n6\\n\", \"6\\n13\\n5\\n\", \"7\\n12\\n4\\n\", \"6\\n11\\n4\\n\", \"7\\n9\\n6\\n\", \"5\\n14\\n2\\n\", \"5\\n11\\n5\\n\", \"5\\n12\\n3\\n\", \"2\\n9\\n12\\n\", \"7\\n12\\n5\\n\", \"5\\n8\\n2\\n\", \"7\\n11\\n5\\n\", \"3\\n6\\n3\\n\", \"3\\n12\\n3\\n\", \"5\\n4\\n4\\n\", \"6\\n13\\n7\\n\", \"8\\n10\\n6\\n\", \"6\\n11\\n7\\n\", \"2\\n9\\n6\\n\", \"4\\n9\\n5\\n\", \"3\\n13\\n4\\n\", \"7\\n18\\n5\\n\", \"8\\n9\\n6\\n\", \"3\\n7\\n3\\n\", \"2\\n9\\n13\\n\", \"5\\n12\\n5\\n\", \"2\\n9\\n5\\n\", \"6\\n9\\n6\\n\", \"5\\n8\\n9\\n\", \"4\\n7\\n3\\n\", \"5\\n5\\n7\\n\", \"6\\n8\\n9\\n\", \"5\\n8\\n3\\n\", \"6\\n8\\n10\\n\", \"5\\n4\\n2\\n\", \"2\\n11\\n13\\n\", \"6\\n9\\n2\\n\", \"7\\n12\\n6\\n\", \"6\\n5\\n10\\n\", \"2\\n11\\n19\\n\", \"6\\n4\\n10\\n\", \"2\\n11\\n21\\n\", \"6\\n7\\n2\\n\", \"10\\n9\\n8\\n\", \"7\\n10\\n4\\n\", \"6\\n4\\n15\\n\", \"5\\n10\\n4\\n\", \"2\\n11\\n20\\n\", \"10\\n11\\n8\\n\", \"6\\n8\\n2\\n\", \"6\\n3\\n15\\n\", \"6\\n3\\n16\\n\", \"5\\n9\\n6\"]}", "source": "taco"}
|
Read problems statements in Mandarin Chinese and Russian.
Suraj, the Chief Prankster is back in action now and this time he has stolen the valentine's day gift given by Ashi (the love of Chef) to the Chef and ran away with it to Byteland.
Byteland is a not a regular place like Chef's town. The safest way from Chef's town to Byteland is through the path of tasty dishes. The path is named so because there are magical tasty dishes which appear to the traveler that no one can resist eating. Also, Suraj has added a strong sleep potion to each of the dish on this path to stop anyone from following him.
Knowing the devilish nature of Suraj, Ashi is concerned about the Chef and has asked all of Chef's town people to help. The distance from Chef's town to Byteland through the the path of tasty dishes is X units. They have the location where the magic dishes are and how many people are required to eat it completely. Anyone who eats a dish would go to a long sleep and won't be able to continue. They have the information about the tribal clans that live along the the path of tasty dishes who can be of real help in this journey.
The journey Chef and his friends can be described as follows: There is a total of B dishes on the path of tasty dishes. Each dish is located at some distance from Chef's town denoted by x_{i} for the i^{th} dish ( x_{i-1} < x_{i}). To minimize the number of friends Chef has to leave behind, all of them have decided that exactly y_{i} of them will eat the i^{th} dish, which is the required number of people needed to finish it completely. Also, there are a total of C tribal chef clans, each with their own population and location on the path that Chef and his friends will meet on their way to Byteland. They know that for some clan (say i), they are located at a distance of p_{i} ( p_{i-1} < p_{i}) from Chef's town with a population of r_{i}. And if a group of at least q_{i} men approaches them, they would be able to convince them to join their forces against Suraj.
Given the information about all this, help the Chef to find out the minimum size of the group (including him and his friends) he should start with to reach Byteland and get back Ashi's gift from Suraj.
------ Input ------
The first line of the input contains an integer T denoting the number of test cases. Each test case contains three lines which are as follows:
First line of each test case contains X, the distance of Byteland from Chef's town.
Next line contains an integer B, the number of dishes on the path of tasty dishes. Then follows B pairs of space separated integers of the form x_{i} y_{i}, where x_{i} y_{i} are as defined above for the i^{th} dish.
Next line contains an integer C, followed C space separated triplets of integers p_{i} q_{i} r_{i} as defined above.
------ Output ------
For each test case, print the minimum size of the group (including Chef) that is needed to reach Byteland.
------ Constraints ------
1 ≤ T ≤ 10
1 ≤ X ≤ 10^{9}
1 ≤ B ≤ 10000
Constraints on C
Subproblem 1 (25 points): C = 0
Subproblem 2 (75 points): 1 ≤ C ≤ 10000
1 ≤ x_{i} < X, x_{i} < x_{i+1}
1 ≤ p_{i} < X, p_{i} < p_{i+1}
1 ≤ y_{i} ≤ 10^{14}
1 ≤ q_{i} ≤ 10^{14}
1 ≤ r_{i} ≤ 10^{14}
All the positions, of the tasty dishes and tribal clans are distinct.
----- Sample Input 1 ------
3
10
2 1 3 8 1
0
10
2 1 3 8 5
0
10
2 2 3 8 5
3 1 2 1 4 3 2 9 1 1
----- Sample Output 1 ------
5
9
6
----- explanation 1 ------
Example case 1. In the first case, there are no tribal clans, and two dishes, one which needs to be eaten by 3 chefs on their way and one to be eaten by 1 chef. Hence, we have to start with atleast 5 people in total to pass the path of tasty dishes.
Example case 2. Similar as Example Case 1.
Example case 3. In this case, if we start with 5 Chefs. At point 1, we have more than or equal to 2 chefs, hence the tribal clan of size 1 adds to the Chef's party and now they have size of 6. At position 2, three of them would be left behind eating a dish, leaving 3 of them to go ahead. At position 4, since the size is exactly 3, the tribal clan joins the chef's party making it of size 5. At position 8, all 5 of them will stop to eat the dish and none would go ahead. Similarly, if we start with 6, one of them would be able to pass position 8 and reach position 9, where it will also add one of the tribal clans to its party and reach Byteland.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"6 1\\n2\\n1\\n3\", \"5 1\\n2\\n1\\n0\", \"6 1\\n2\\n1\\n4\", \"5 1\\n1\\n1\\n0\", \"6 1\\n2\\n1\\n8\", \"5 1\\n1\\n1\\n1\", \"7 1\\n1\\n1\\n0\", \"8 1\\n1\\n1\\n0\", \"10 1\\n1\\n1\\n1\", \"11 1\\n6\\n1\\n5\", \"15 1\\n3\\n1\\n2\", \"15 1\\n6\\n1\\n5\", \"15 1\\n3\\n1\\n3\", \"15 1\\n1\\n1\\n0\", \"15 1\\n1\\n1\\n1\", \"25 1\\n1\\n1\\n1\", \"15 1\\n2\\n1\\n4\", \"23 1\\n3\\n1\\n2\", \"2 1\\n2\\n1\\n0\", \"6 1\\n4\\n1\\n4\", \"5 1\\n3\\n1\\n3\", \"5 1\\n3\\n1\\n1\", \"6 1\\n1\\n1\\n4\", \"5 1\\n3\\n1\\n5\", \"5 1\\n3\\n1\\n4\", \"6 1\\n2\\n1\\n0\", \"2 1\\n2\\n1\\n1\", \"2 1\\n4\\n1\\n4\", \"5 1\\n3\\n1\\n0\", \"6 1\\n3\\n1\\n3\", \"5 1\\n3\\n1\\n10\", \"7 1\\n2\\n1\\n0\", \"2 1\\n0\\n1\\n1\", \"2 1\\n0\\n1\\n4\", \"9 1\\n3\\n1\\n1\", \"3 1\\n2\\n1\\n0\", \"6 1\\n6\\n1\\n4\", \"5 1\\n5\\n1\\n3\", \"6 1\\n3\\n1\\n8\", \"5 1\\n1\\n1\\n5\", \"4 1\\n1\\n1\\n1\", \"5 1\\n0\\n1\\n4\", \"9 1\\n2\\n1\\n0\", \"2 1\\n3\\n1\\n10\", \"15 1\\n3\\n1\\n1\", \"6 1\\n5\\n1\\n8\", \"2 1\\n2\\n1\\n10\", \"11 1\\n5\\n1\\n8\", \"11 1\\n6\\n1\\n8\", \"11 1\\n6\\n1\\n16\", \"7 1\\n2\\n1\\n3\", \"2 1\\n2\\n1\\n3\", \"7 1\\n4\\n1\\n0\", \"6 1\\n2\\n1\\n2\", \"2 1\\n1\\n1\\n0\", \"5 1\\n2\\n1\\n1\", \"9 1\\n3\\n1\\n4\", \"10 1\\n3\\n1\\n0\", \"9 1\\n1\\n1\\n0\", \"5 1\\n3\\n1\\n12\", \"6 1\\n3\\n1\\n4\", \"5 1\\n0\\n1\\n5\", \"5 1\\n1\\n1\\n4\", \"2 1\\n0\\n1\\n10\", \"11 1\\n7\\n1\\n8\", \"11 1\\n6\\n1\\n6\", \"11 1\\n8\\n1\\n16\", \"2 1\\n2\\n1\\n6\", \"10 1\\n2\\n1\\n0\", \"6 1\\n1\\n1\\n1\", \"17 1\\n3\\n1\\n0\", \"5 1\\n0\\n1\\n7\", \"2 1\\n1\\n1\\n10\", \"11 1\\n3\\n1\\n8\", \"11 1\\n7\\n1\\n16\", \"3 1\\n1\\n1\\n10\", \"11 1\\n6\\n1\\n3\", \"11 1\\n6\\n1\\n4\", \"7 1\\n3\\n1\\n3\", \"6 1\\n4\\n1\\n8\", \"6 1\\n1\\n1\\n2\", \"6 1\\n3\\n1\\n0\", \"4 1\\n0\\n1\\n4\", \"7 1\\n6\\n1\\n4\", \"4 1\\n1\\n1\\n0\", \"2 1\\n3\\n1\\n5\", \"5 1\\n5\\n1\\n8\", \"15 1\\n6\\n1\\n16\", \"7 1\\n2\\n1\\n6\", \"6 1\\n2\\n1\\n1\", \"10 1\\n6\\n1\\n0\", \"9 1\\n1\\n1\\n1\", \"6 1\\n4\\n1\\n7\", \"11 1\\n11\\n1\\n16\", \"11 1\\n11\\n1\\n6\", \"2 1\\n2\\n1\\n7\", \"11 1\\n0\\n1\\n16\", \"3 1\\n0\\n1\\n10\", \"11 1\\n6\\n1\\n1\", \"6 1\\n4\\n1\\n9\", \"5 1\\n2\\n1\\n3\"], \"outputs\": [\"3\\n\", \"-1\\n\", \"2\\n\", \"5\\n\", \"1\\n\", \"4\\n\", \"7\\n\", \"8\\n\", \"9\\n\", \"6\\n\", \"13\\n\", \"10\\n\", \"12\\n\", \"15\\n\", \"14\\n\", \"24\\n\", \"11\\n\", \"21\\n\", \"-1\\n\", \"2\\n\", \"2\\n\", \"-1\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"3\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"3\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"3\\n\", \"3\\n\", \"1\\n\", \"4\\n\", \"1\\n\", \"-1\\n\", \"4\\n\", \"2\\n\", \"4\\n\", \"5\\n\", \"-1\\n\", \"9\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"3\\n\", \"5\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"5\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"3\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"-1\\n\", \"4\\n\", \"1\\n\", \"4\\n\", \"-1\\n\", \"1\\n\", \"-1\\n\", \"4\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"5\\n\", \"-1\\n\", \"8\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"2\"]}", "source": "taco"}
|
D: Arrow / Arrow
problem
rodea is in a one-dimensional coordinate system and stands at x = 0. From this position, throw an arrow of positive integer length that always moves at speed 1 towards the target at x = N. However, rodea is powerless, so we have decided to put a total of M blowers in the section 0 \ leq x \ leq N.
Here, the case where one blower is not included in the position from the tip to the base of the arrow is defined as "loss". The loss is determined when the tip of the arrow reaches x = 1, 2, 3, $ \ ldots $, N (that is, a total of N times).
At this time, process the following query Q times.
* "Loss" Given the acceptable number of times l_i. In other words, if the total "loss" is l_i times or less in N judgments, it is possible to deliver the arrow. At this time, find the shortest arrow length required to deliver the arrow.
Input format
N M
m_1 m_2 $ \ ldots $ m_M
Q
l_1 l_2 $ \ ldots $ l_Q
The distance N and the number of blowers M are given on the first line, separated by blanks.
The second line gives the position of each of the M blowers. When m_i = j, the i-th blower is located exactly between x = j-1 and x = j.
The third line gives the number of queries Q, and the fourth line gives Q the acceptable number of "losses" l_i.
Constraint
* 1 \ leq N \ leq 10 ^ 5
* 1 \ leq M \ leq N
* 1 \ leq m_1 <m_2 <$ \ ldots $ <m_M \ leq N
* 1 \ leq Q \ leq 10 ^ 5
* 0 \ leq l_i \ leq 10 ^ 5 (1 \ leq i \ leq Q)
Output format
Output the shortest possible arrow lengths for a given Q l_i, in order, with a newline.
However, if there is no arrow with a length of a positive integer that satisfies the condition, -1 shall be output.
Input example 1
5 1
2
1
3
Output example 1
2
When the tip of the arrow reaches x = 1, the number of "losses" is 1 because the blower is not included from the tip to the base.
When the tip of the arrow reaches x = 2, the number of "losses" remains 1 because the blower is included from the tip to the base.
When the tip of the arrow reaches x = 3, the number of "losses" remains 1 because the blower is included from the tip to the base.
When the tip of the arrow reaches x = 4, the number of "losses" is 2 because the blower is not included from the tip to the base.
When the tip of the arrow reaches x = 5, the number of "losses" is 3 because the blower is not included from the tip to the base.
When throwing an arrow shorter than length 2, the number of "losses" is greater than 3, so throwing an arrow of length 2 is the shortest arrow length that meets the condition.
Input example 2
11 3
2 5 9
3
1 4 8
Output example 2
Four
3
1
Example
Input
5 1
2
1
3
Output
2
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"5\\n3 1\\n1 1\\n-1 0\\n2 1\\n3 0\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n2 0\\n3 0\\n\", \"8\\n2 1\\n-1 0\\n1 0\\n1 1\\n1 1\\n4 0\\n5 1\\n7 0\\n\", \"1\\n-1 0\\n\", \"1\\n-1 0\\n\", \"5\\n-1 0\\n1 0\\n1 1\\n2 0\\n3 0\\n\", \"8\\n2 1\\n-1 0\\n1 1\\n1 1\\n1 1\\n4 0\\n5 1\\n7 0\\n\", \"8\\n2 1\\n-1 0\\n1 0\\n1 1\\n2 1\\n4 0\\n5 1\\n7 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n2 1\\n3 1\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n2 0\\n2 0\\n\", \"8\\n2 1\\n-1 0\\n1 0\\n1 1\\n2 1\\n4 0\\n5 1\\n7 1\\n\", \"5\\n3 0\\n1 1\\n-1 0\\n2 1\\n3 1\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n3 1\\n3 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n2 0\\n3 1\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n2 1\\n3 0\\n\", \"8\\n2 1\\n-1 0\\n1 1\\n1 1\\n1 1\\n4 0\\n5 1\\n7 1\\n\", \"5\\n-1 0\\n1 1\\n4 1\\n2 1\\n1 0\\n\", \"5\\n-1 0\\n1 1\\n2 1\\n1 0\\n4 0\\n\", \"5\\n3 1\\n1 0\\n-1 0\\n2 1\\n3 1\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n3 1\\n2 0\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n3 0\\n4 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n1 0\\n3 1\\n\", \"5\\n-1 0\\n1 0\\n1 0\\n2 1\\n3 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n3 0\\n3 0\\n\", \"8\\n2 0\\n-1 0\\n1 1\\n1 1\\n1 1\\n4 0\\n2 1\\n7 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n2 0\\n3 0\\n\", \"5\\n-1 0\\n1 1\\n2 1\\n2 0\\n2 0\\n\", \"5\\n-1 0\\n1 0\\n1 1\\n3 0\\n3 0\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n2 0\\n1 0\\n\", \"5\\n-1 0\\n1 1\\n2 1\\n3 0\\n2 0\\n\", \"5\\n-1 0\\n1 0\\n2 1\\n3 0\\n3 0\\n\", \"5\\n3 0\\n1 1\\n-1 0\\n3 1\\n3 1\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n3 0\\n2 0\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n2 0\\n3 0\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n2 0\\n2 0\\n\", \"5\\n-1 0\\n1 1\\n2 1\\n2 0\\n1 0\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n2 0\\n2 1\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n2 1\\n2 1\\n\", \"5\\n3 0\\n1 1\\n-1 0\\n2 1\\n3 0\\n\", \"8\\n2 1\\n-1 0\\n1 0\\n1 1\\n1 1\\n4 0\\n6 1\\n7 0\\n\", \"5\\n-1 0\\n1 1\\n2 1\\n2 0\\n3 0\\n\", \"5\\n-1 0\\n1 1\\n2 1\\n5 0\\n2 0\\n\", \"5\\n3 0\\n1 1\\n-1 0\\n2 0\\n3 1\\n\", \"5\\n-1 0\\n1 0\\n1 0\\n2 0\\n2 0\\n\", \"5\\n-1 0\\n1 1\\n4 1\\n2 0\\n1 0\\n\", \"8\\n2 1\\n-1 0\\n1 0\\n1 1\\n1 1\\n4 0\\n2 1\\n7 0\\n\", \"5\\n-1 0\\n1 1\\n2 1\\n2 0\\n4 0\\n\", \"5\\n-1 0\\n1 0\\n2 1\\n3 0\\n2 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n3 1\\n3 1\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n2 0\\n4 0\\n\", \"5\\n-1 0\\n1 1\\n2 0\\n2 1\\n2 1\\n\", \"5\\n-1 0\\n1 1\\n2 0\\n5 0\\n2 0\\n\", \"5\\n-1 0\\n1 1\\n4 1\\n2 0\\n2 0\\n\", \"8\\n2 0\\n-1 0\\n1 0\\n1 1\\n1 1\\n4 0\\n2 1\\n7 0\\n\", \"5\\n-1 0\\n1 1\\n2 1\\n1 0\\n2 0\\n\", \"5\\n-1 0\\n1 1\\n2 1\\n3 1\\n2 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n1 1\\n3 1\\n\", \"5\\n-1 0\\n1 0\\n1 0\\n2 1\\n1 0\\n\", \"5\\n-1 0\\n1 1\\n2 0\\n1 0\\n2 0\\n\", \"5\\n-1 0\\n1 0\\n2 0\\n2 1\\n1 0\\n\", \"8\\n2 1\\n-1 0\\n1 0\\n1 1\\n1 1\\n4 0\\n1 1\\n7 0\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n3 0\\n3 0\\n\", \"5\\n-1 0\\n1 0\\n1 1\\n2 1\\n3 0\\n\", \"5\\n-1 0\\n1 0\\n1 1\\n3 0\\n2 0\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n1 0\\n2 1\\n\", \"5\\n3 0\\n1 1\\n-1 0\\n2 1\\n1 0\\n\", \"5\\n-1 0\\n1 0\\n2 1\\n2 0\\n3 0\\n\", \"5\\n3 0\\n1 0\\n-1 0\\n2 0\\n3 1\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n2 1\\n2 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n1 0\\n2 1\\n\", \"5\\n-1 0\\n1 1\\n2 0\\n3 1\\n2 1\\n\", \"5\\n-1 0\\n1 0\\n1 0\\n2 1\\n1 1\\n\", \"5\\n-1 0\\n1 1\\n2 0\\n2 1\\n1 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n2 1\\n1 0\\n\", \"5\\n-1 0\\n1 1\\n2 0\\n3 1\\n2 0\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n2 1\\n1 0\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n2 1\\n1 1\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n2 1\\n2 0\\n\", \"5\\n-1 0\\n1 0\\n1 1\\n3 0\\n1 0\\n\", \"5\\n-1 0\\n1 0\\n2 1\\n3 0\\n1 0\\n\", \"5\\n3 0\\n1 1\\n-1 0\\n3 1\\n3 0\\n\", \"5\\n-1 0\\n1 1\\n1 0\\n2 1\\n4 0\\n\", \"5\\n-1 0\\n1 1\\n4 1\\n2 0\\n1 1\\n\", \"5\\n-1 0\\n1 1\\n2 0\\n2 0\\n4 0\\n\", \"5\\n3 0\\n1 0\\n-1 0\\n2 1\\n3 1\\n\", \"5\\n-1 0\\n1 0\\n2 1\\n1 0\\n2 0\\n\", \"5\\n3 1\\n1 1\\n-1 0\\n2 1\\n3 0\\n\", \"8\\n2 1\\n-1 0\\n1 0\\n1 1\\n1 1\\n4 0\\n5 1\\n7 0\\n\", \"5\\n-1 0\\n1 1\\n1 1\\n2 0\\n3 0\\n\"], \"outputs\": [\"1 2 4 \\n\", \"-1\\n\", \"5 \\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"1 3 5\\n\", \"5\\n\", \"1 2 4 5\\n\", \"3\\n\", \"5 7 8\\n\", \"2 4 5\\n\", \"1 2 4\\n\", \"1 5\\n\", \"2 4\\n\", \"1 3 5 7 8\\n\", \"2 3 4\\n\", \"2 3\\n\", \"4 5\\n\", \"3 4\\n\", \"2\\n\", \"2 5\\n\", \"4\\n\", \"1 2\\n\", \"3 5\\n\", \"1\\n\", \"3\\n\", \"-1\\n\", \"3\\n\", \"-1\\n\", \"-1\\n\", \"2 4 5\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"3\\n\", \"5\\n\", \"2 4 5\\n\", \"2 4\\n\", \"5\\n\", \"-1\\n\", \"3\\n\", \"5\\n\", \"-1\\n\", \"3\\n\", \"5\\n\", \"3\\n\", \"-1\\n\", \"1 2 4 5\\n\", \"3\\n\", \"4 5\\n\", \"-1\\n\", \"3\\n\", \"5\\n\", \"3\\n\", \"3 4\\n\", \"1 2 4 5\\n\", \"4\\n\", \"-1\\n\", \"4\\n\", \"5\\n\", \"2\\n\", \"4\\n\", \"-1\\n\", \"2 5\\n\", \"2 4\\n\", \"-1\\n\", \"5\\n\", \"3 4\\n\", \"2 5\\n\", \"4 5\\n\", \"4 5\\n\", \"4\\n\", \"2 4\\n\", \"4\\n\", \"2 4\\n\", \"2 4 5\\n\", \"4\\n\", \"-1\\n\", \"-1\\n\", \"2 4\\n\", \"2\\n\", \"3 5\\n\", \"-1\\n\", \"4 5\\n\", \"3\\n\", \"1 2 4\\n\", \"5\\n\", \"-1\\n\"]}", "source": "taco"}
|
You are given a rooted tree with vertices numerated from $1$ to $n$. A tree is a connected graph without cycles. A rooted tree has a special vertex named root.
Ancestors of the vertex $i$ are all vertices on the path from the root to the vertex $i$, except the vertex $i$ itself. The parent of the vertex $i$ is the nearest to the vertex $i$ ancestor of $i$. Each vertex is a child of its parent. In the given tree the parent of the vertex $i$ is the vertex $p_i$. For the root, the value $p_i$ is $-1$.
[Image] An example of a tree with $n=8$, the root is vertex $5$. The parent of the vertex $2$ is vertex $3$, the parent of the vertex $1$ is vertex $5$. The ancestors of the vertex $6$ are vertices $4$ and $5$, the ancestors of the vertex $7$ are vertices $8$, $3$ and $5$
You noticed that some vertices do not respect others. In particular, if $c_i = 1$, then the vertex $i$ does not respect any of its ancestors, and if $c_i = 0$, it respects all of them.
You decided to delete vertices from the tree one by one. On each step you select such a non-root vertex that it does not respect its parent and none of its children respects it. If there are several such vertices, you select the one with the smallest number. When you delete this vertex $v$, all children of $v$ become connected with the parent of $v$.
[Image] An example of deletion of the vertex $7$.
Once there are no vertices matching the criteria for deletion, you stop the process. Print the order in which you will delete the vertices. Note that this order is unique.
-----Input-----
The first line contains a single integer $n$ ($1 \le n \le 10^5$) — the number of vertices in the tree.
The next $n$ lines describe the tree: the $i$-th line contains two integers $p_i$ and $c_i$ ($1 \le p_i \le n$, $0 \le c_i \le 1$), where $p_i$ is the parent of the vertex $i$, and $c_i = 0$, if the vertex $i$ respects its parents, and $c_i = 1$, if the vertex $i$ does not respect any of its parents. The root of the tree has $-1$ instead of the parent index, also, $c_i=0$ for the root. It is guaranteed that the values $p_i$ define a rooted tree with $n$ vertices.
-----Output-----
In case there is at least one vertex to delete, print the only line containing the indices of the vertices you will delete in the order you delete them. Otherwise print a single integer $-1$.
-----Examples-----
Input
5
3 1
1 1
-1 0
2 1
3 0
Output
1 2 4
Input
5
-1 0
1 1
1 1
2 0
3 0
Output
-1
Input
8
2 1
-1 0
1 0
1 1
1 1
4 0
5 1
7 0
Output
5
-----Note-----
The deletion process in the first example is as follows (see the picture below, the vertices with $c_i=1$ are in yellow):
first you will delete the vertex $1$, because it does not respect ancestors and all its children (the vertex $2$) do not respect it, and $1$ is the smallest index among such vertices; the vertex $2$ will be connected with the vertex $3$ after deletion; then you will delete the vertex $2$, because it does not respect ancestors and all its children (the only vertex $4$) do not respect it; the vertex $4$ will be connected with the vertex $3$; then you will delete the vertex $4$, because it does not respect ancestors and all its children (there are none) do not respect it (vacuous truth); you will just delete the vertex $4$; there are no more vertices to delete.
[Image]
In the second example you don't need to delete any vertex:
vertices $2$ and $3$ have children that respect them; vertices $4$ and $5$ respect ancestors.
[Image]
In the third example the tree will change this way:
[Image]
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.75
|
{"tests": "{\"inputs\": [\"5\\n3 21 14 5 13\", \"5\\n2 3 24 6 13\", \"5\\n2 3 38 3 10\", \"5\\n3 24 14 5 13\", \"5\\n3 24 14 10 13\", \"5\\n3 24 16 10 13\", \"5\\n3 36 16 10 13\", \"5\\n3 36 16 14 13\", \"5\\n3 3 16 14 13\", \"5\\n3 3 24 14 13\", \"5\\n3 3 24 6 13\", \"5\\n2 3 24 6 9\", \"5\\n2 3 24 6 14\", \"5\\n2 3 38 6 14\", \"5\\n2 3 38 6 10\", \"5\\n2 3 2 3 10\", \"5\\n4 3 2 3 10\", \"5\\n6 3 2 3 10\", \"3\\n1 4 3\", \"5\\n3 11 14 5 1\", \"5\\n3 18 14 5 13\", \"5\\n3 24 15 5 13\", \"5\\n3 34 14 10 13\", \"5\\n3 24 16 16 13\", \"5\\n3 36 3 10 13\", \"5\\n3 36 18 14 13\", \"5\\n3 3 2 14 13\", \"5\\n3 3 24 8 13\", \"5\\n1 3 24 6 13\", \"5\\n2 3 24 6 7\", \"5\\n2 2 24 6 9\", \"5\\n2 3 24 6 16\", \"5\\n2 3 38 6 6\", \"5\\n2 3 76 6 10\", \"5\\n2 3 25 3 10\", \"5\\n2 3 3 3 10\", \"5\\n4 3 4 3 10\", \"5\\n6 3 1 3 10\", \"3\\n1 4 1\", \"5\\n3 11 14 10 1\", \"5\\n3 18 14 5 5\", \"5\\n3 24 22 5 13\", \"5\\n1 34 14 10 13\", \"5\\n2 24 16 16 13\", \"5\\n3 36 3 10 15\", \"5\\n3 4 18 14 13\", \"5\\n3 3 0 14 13\", \"5\\n3 4 24 8 13\", \"5\\n1 3 45 6 13\", \"5\\n3 3 24 6 7\", \"5\\n2 2 1 6 9\", \"5\\n2 6 24 6 16\", \"5\\n2 3 38 6 8\", \"5\\n2 3 16 6 10\", \"5\\n2 6 25 3 10\", \"5\\n2 3 3 3 19\", \"5\\n7 3 4 3 10\", \"5\\n6 3 1 3 5\", \"5\\n3 11 19 10 1\", \"5\\n3 18 14 5 2\", \"5\\n3 24 22 5 16\", \"5\\n0 34 14 10 13\", \"5\\n2 24 16 16 1\", \"5\\n3 36 2 10 15\", \"5\\n3 4 1 14 13\", \"5\\n3 3 1 14 13\", \"5\\n3 7 24 8 13\", \"5\\n1 3 82 6 13\", \"5\\n3 3 24 1 7\", \"5\\n2 2 1 5 9\", \"5\\n2 6 24 5 16\", \"5\\n2 3 38 1 8\", \"5\\n2 3 16 6 20\", \"5\\n2 6 25 5 10\", \"5\\n2 3 6 3 19\", \"5\\n7 3 8 3 10\", \"5\\n6 2 1 3 5\", \"5\\n3 18 14 5 3\", \"5\\n3 24 22 1 16\", \"5\\n1 34 14 10 25\", \"5\\n2 41 16 16 1\", \"5\\n3 36 2 10 8\", \"5\\n3 3 1 14 20\", \"5\\n4 7 24 8 13\", \"5\\n1 4 82 6 13\", \"5\\n3 3 24 2 7\", \"5\\n2 2 1 5 6\", \"5\\n2 6 24 5 9\", \"5\\n2 3 38 1 1\", \"5\\n4 3 16 6 20\", \"5\\n2 4 25 5 10\", \"5\\n3 3 6 3 19\", \"5\\n7 3 8 3 19\", \"5\\n4 2 1 3 5\", \"5\\n4 18 14 5 3\", \"5\\n3 24 9 1 16\", \"5\\n1 34 26 10 25\", \"5\\n2 20 16 16 1\", \"5\\n3 26 2 10 8\", \"5\\n3 3 0 14 20\", \"3\\n1 2 3\", \"5\\n3 11 14 5 13\"], \"outputs\": [\"1\\n\", \"2\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"2\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"2\\n\", \"2\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"1\", \"2\"]}", "source": "taco"}
|
Takahashi has N balls with positive integers written on them. The integer written on the i-th ball is A_i. He would like to form some number of pairs such that the sum of the integers written on each pair of balls is a power of 2. Note that a ball cannot belong to multiple pairs. Find the maximum possible number of pairs that can be formed.
Here, a positive integer is said to be a power of 2 when it can be written as 2^t using some non-negative integer t.
Constraints
* 1 \leq N \leq 2\times 10^5
* 1 \leq A_i \leq 10^9
* A_i is an integer.
Input
Input is given from Standard Input in the following format:
N
A_1 A_2 ... A_N
Output
Print the maximum possible number of pairs such that the sum of the integers written on each pair of balls is a power of 2.
Examples
Input
3
1 2 3
Output
1
Input
5
3 11 14 5 13
Output
2
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[\"Carlos Ray Norris\", \"Carlos Ray Norris\"], [\"Carlos Ray Norris\", \"Carlos Ray\"], [\"Carlos Ray Norris\", \"Ray Norris\"], [\"Carlos Ray Norris\", \"Carlos Norris\"], [\"Carlos Ray Norris\", \"Norris\"], [\"Carlos Ray Norris\", \"Carlos\"], [\"Carlos Ray Norris\", \"Norris Carlos\"], [\"Carlos Ray Norris\", \"carlos ray norris\"], [\"Carlos Ray Norris\", \"Norris! ?ray\"], [\"Carlos Ray Norris\", \"Carlos. Ray; Norris,\"], [\"Carlos Ray Norris\", \"Carlos:Ray Norris\"], [\"Carlos-Ray Norris\", \"Carlos-Ray Norris:\"], [\"Carlos Ray-Norris\", \"Carlos? Ray-Norris\"], [\"Carlos Ray Norris\", \"Carlos Ray Norr\"], [\"Carlos Ray Norris\", \"Ra Norris\"], [\"\", \"C\"], [\"\", \"\"], [\"Carlos Ray Norris\", \" \"], [\"Carlos-Ray Norris\", \"Carlos Ray-Norris\"], [\"Carlos Ray Norris\", \"Carlos-Ray Norris\"], [\"Carlos Ray Norris\", \"Carlos Ray-Norris\"], [\"Carlos Ray\", \"Carlos Ray Norris\"], [\"Carlos\", \"Carlos Ray Norris\"]], \"outputs\": [[true], [true], [true], [true], [true], [true], [true], [true], [true], [true], [true], [true], [true], [false], [false], [false], [false], [false], [false], [false], [false], [false], [false]]}", "source": "taco"}
|
The objective is to disambiguate two given names: the original with another
This kata is slightly more evolved than the previous one: [Author Disambiguation: to the point!](https://www.codewars.com/kata/580a429e1cb4028481000019).
The function ```could_be``` is still given the original name and another one to test
against.
```python
# should return True even with 'light' variations (more details in section below)
> could_be("Chuck Norris", u"chück!")
True
# should False otherwise (whatever you may personnaly think)
> could_be("Chuck Norris", "superman")
False
```
**Watch out**: When accents comes into the game, they will enter through **UTF-8 unicodes. **
The function should be tolerant with regards to:
* upper and lower cases: ```could_be(A, a) : True```
* accents: ```could_be(E, é) : True```
* dots: ```could_be(E., E) : True```
* same for other ending punctuations in [!,;:?]: ```could_be(A, A!) : True```
On the other hand, more consideration needs to be given to *composed names*...
Let's be bold about it: if you have any, they will be considered as a whole :
```python
# We still have:
> could_be("Carlos Ray Norris", "Carlos Ray Norris")
True
> could_be("Carlos-Ray Norris", "Carlos-Ray Norris")
True
# But:
> could_be("Carlos Ray Norris", "Carlos-Ray Norris")
False
> could_be("Carlos-Ray Norris", "Carlos Ray Norris")
False
> could_be("Carlos-Ray Norris", "Carlos Ray-Norris")
False
```
Among the valid combinaisons of the fullname "Carlos Ray Norris", you will find
```python
could_be("Carlos Ray Norris", "carlos ray") : True
could_be("Carlos Ray Norris", "Carlos. Ray, Norris;") : True
could_be("Carlos Ray Norris", u"Carlòs! Norris") : True
```
Too easy ? Try the next step: [Author Disambiguation: Signatures worth it](https://www.codewars.com/kata/author-disambiguation-signatures-worth-it)
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\\n1 3\\n3 3\\n4 3\", \"3\\n2 4\\n3 3\\n4 3\", \"3\\n2 4\\n3 3\\n3 3\", \"3\\n1 4\\n3 2\\n4 3\", \"3\\n2 4\\n3 6\\n3 3\", \"3\\n2 2\\n3 2\\n2 3\", \"3\\n4 4\\n3 6\\n3 3\", \"3\\n2 2\\n4 2\\n1 3\", \"3\\n1 3\\n3 3\\n4 4\", \"3\\n1 4\\n3 7\\n4 3\", \"3\\n1 5\\n3 2\\n3 3\", \"3\\n1 1\\n3 3\\n4 4\", \"3\\n1 5\\n3 3\\n3 3\", \"3\\n1 5\\n3 3\\n4 3\", \"3\\n1 9\\n3 14\\n4 3\", \"3\\n1 4\\n5 3\\n4 3\", \"3\\n1 4\\n9 3\\n4 3\", \"3\\n1 9\\n4 4\\n4 3\", \"3\\n1 9\\n4 4\\n1 3\", \"3\\n1 9\\n8 4\\n1 3\", \"3\\n1 9\\n8 5\\n1 5\", \"3\\n1 9\\n8 5\\n1 9\", \"3\\n1 9\\n8 5\\n1 1\", \"3\\n1 9\\n1 5\\n1 1\", \"3\\n1 9\\n1 3\\n1 1\", \"3\\n1 3\\n3 2\\n4 3\", \"3\\n2 2\\n3 3\\n4 3\", \"3\\n2 2\\n4 4\\n1 3\", \"3\\n1 3\\n3 2\\n4 4\", \"3\\n1 8\\n3 11\\n4 3\", \"3\\n1 7\\n8 5\\n1 5\", \"3\\n1 9\\n1 3\\n1 2\", \"3\\n1 13\\n1 4\\n2 2\", \"3\\n2 3\\n4 3\\n1 3\", \"3\\n1 8\\n5 11\\n4 3\", \"3\\n2 7\\n8 5\\n1 5\", \"3\\n1 13\\n1 5\\n2 2\", \"3\\n1 3\\n4 3\\n1 3\", \"3\\n1 13\\n1 5\\n2 3\", \"3\\n1 3\\n5 3\\n1 3\", \"3\\n1 19\\n3 6\\n3 3\", \"3\\n1 6\\n9 6\\n7 5\", \"3\\n1 13\\n1 2\\n2 3\", \"3\\n1 11\\n5 11\\n4 5\", \"3\\n1 7\\n8 5\\n2 5\", \"3\\n1 11\\n5 11\\n3 5\", \"3\\n1 1\\n8 1\\n3 5\", \"3\\n6 4\\n6 6\\n3 5\", \"3\\n6 4\\n7 6\\n3 5\", \"3\\n1 1\\n29 1\\n3 2\", \"3\\n1 1\\n19 1\\n3 2\", \"3\\n2 1\\n19 1\\n3 4\", \"3\\n1 4\\n3 7\\n5 3\", \"3\\n1 4\\n3 14\\n7 3\", \"3\\n1 4\\n9 3\\n5 3\", \"3\\n1 6\\n4 4\\n1 3\", \"3\\n1 9\\n1 5\\n1 2\", \"3\\n1 17\\n1 4\\n1 2\", \"3\\n1 15\\n1 8\\n2 2\", \"3\\n1 5\\n3 2\\n4 3\", \"3\\n2 2\\n3 3\\n7 3\", \"3\\n1 1\\n1 3\\n3 4\", \"3\\n1 4\\n9 5\\n4 5\", \"3\\n1 7\\n15 5\\n2 5\", \"3\\n1 17\\n1 3\\n1 2\", \"3\\n1 8\\n3 11\\n3 3\", \"3\\n6 4\\n3 1\\n3 1\", \"3\\n2 13\\n1 5\\n2 2\", \"3\\n2 2\\n3 3\\n1 7\", \"3\\n1 7\\n5 11\\n4 5\", \"3\\n1 19\\n3 6\\n3 6\", \"3\\n3 7\\n8 7\\n2 5\", \"3\\n1 13\\n1 3\\n2 3\", \"3\\n1 9\\n5 11\\n4 5\", \"3\\n1 13\\n1 3\\n2 2\", \"3\\n2 11\\n5 11\\n3 5\", \"3\\n1 1\\n19 1\\n3 1\", \"3\\n1 4\\n1 3\\n4 4\", \"3\\n1 4\\n3 7\\n5 5\", \"3\\n1 4\\n3 9\\n7 3\", \"3\\n1 1\\n5 3\\n4 1\", \"3\\n1 3\\n1 3\\n1 2\", \"3\\n2 1\\n3 3\\n7 3\", \"3\\n1 4\\n9 1\\n4 5\", \"3\\n1 17\\n1 3\\n1 3\", \"3\\n3 13\\n1 4\\n2 2\", \"3\\n2 9\\n7 1\\n2 2\", \"3\\n1 3\\n7 3\\n3 4\", \"3\\n1 12\\n9 5\\n1 3\", \"3\\n2 3\\n3 3\\n1 7\", \"3\\n2 4\\n3 10\\n7 1\", \"3\\n1 7\\n5 11\\n3 5\", \"3\\n1 19\\n6 6\\n3 6\", \"3\\n1 15\\n8 2\\n3 4\", \"3\\n2 7\\n15 7\\n2 5\", \"3\\n1 4\\n4 7\\n1 9\", \"3\\n3 12\\n13 7\\n1 4\", \"3\\n1 7\\n1 5\\n4 8\", \"3\\n1 5\\n1 3\\n4 13\", \"3\\n1 11\\n3 2\\n2 3\", \"3\\n2 3\\n3 3\\n4 3\"], \"outputs\": [\"2 1\\n1 0\\n1 1\\n\", \"1 1\\n1 0\\n1 1\\n\", \"1 1\\n1 0\\n1 0\\n\", \"1 1\\n1 1\\n1 1\\n\", \"1 1\\n1 1\\n1 0\\n\", \"1 0\\n1 1\\n1 1\\n\", \"1 0\\n1 1\\n1 0\\n\", \"1 0\\n1 1\\n2 1\\n\", \"2 1\\n1 0\\n1 0\\n\", \"1 1\\n11 10\\n1 1\\n\", \"3 2\\n1 1\\n1 0\\n\", \"1 0\\n1 0\\n1 0\\n\", \"3 2\\n1 0\\n1 0\\n\", \"3 2\\n1 0\\n1 1\\n\", \"5 4\\n1 1\\n1 1\\n\", \"1 1\\n8 7\\n1 1\\n\", \"1 1\\n2 1\\n1 1\\n\", \"5 4\\n1 0\\n1 1\\n\", \"5 4\\n1 0\\n2 1\\n\", \"5 4\\n1 1\\n2 1\\n\", \"5 4\\n1 1\\n3 2\\n\", \"5 4\\n1 1\\n5 4\\n\", \"5 4\\n1 1\\n1 0\\n\", \"5 4\\n3 2\\n1 0\\n\", \"5 4\\n2 1\\n1 0\\n\", \"2 1\\n1 1\\n1 1\\n\", \"1 0\\n1 0\\n1 1\\n\", \"1 0\\n1 0\\n2 1\\n\", \"2 1\\n1 1\\n1 0\\n\", \"1 1\\n17 16\\n1 1\\n\", \"4 3\\n1 1\\n3 2\\n\", \"5 4\\n2 1\\n1 1\\n\", \"7 6\\n1 1\\n1 0\\n\", \"1 1\\n1 1\\n2 1\\n\", \"1 1\\n28 27\\n1 1\\n\", \"1 1\\n1 1\\n3 2\\n\", \"7 6\\n3 2\\n1 0\\n\", \"2 1\\n1 1\\n2 1\\n\", \"7 6\\n3 2\\n1 1\\n\", \"2 1\\n8 7\\n2 1\\n\", \"10 9\\n1 1\\n1 0\\n\", \"1 1\\n1 1\\n18 17\\n\", \"7 6\\n1 1\\n1 1\\n\", \"6 5\\n28 27\\n1 1\\n\", \"4 3\\n1 1\\n1 1\\n\", \"6 5\\n28 27\\n8 7\\n\", \"1 0\\n1 1\\n8 7\\n\", \"1 1\\n1 0\\n8 7\\n\", \"1 1\\n1 1\\n8 7\\n\", \"1 0\\n15 14\\n1 1\\n\", \"1 0\\n10 9\\n1 1\\n\", \"1 1\\n10 9\\n1 1\\n\", \"1 1\\n11 10\\n8 7\\n\", \"1 1\\n1 1\\n11 10\\n\", \"1 1\\n2 1\\n8 7\\n\", \"1 1\\n1 0\\n2 1\\n\", \"5 4\\n3 2\\n1 1\\n\", \"9 8\\n1 1\\n1 1\\n\", \"8 7\\n1 1\\n1 0\\n\", \"3 2\\n1 1\\n1 1\\n\", \"1 0\\n1 0\\n11 10\\n\", \"1 0\\n2 1\\n1 1\\n\", \"1 1\\n23 22\\n1 1\\n\", \"4 3\\n2 1\\n1 1\\n\", \"9 8\\n2 1\\n1 1\\n\", \"1 1\\n17 16\\n1 0\\n\", \"1 1\\n2 1\\n2 1\\n\", \"1 1\\n3 2\\n1 0\\n\", \"1 0\\n1 0\\n4 3\\n\", \"4 3\\n28 27\\n1 1\\n\", \"10 9\\n1 1\\n1 1\\n\", \"11 10\\n1 1\\n1 1\\n\", \"7 6\\n2 1\\n1 1\\n\", \"5 4\\n28 27\\n1 1\\n\", \"7 6\\n2 1\\n1 0\\n\", \"1 1\\n28 27\\n8 7\\n\", \"1 0\\n10 9\\n2 1\\n\", \"1 1\\n2 1\\n1 0\\n\", \"1 1\\n11 10\\n1 0\\n\", \"1 1\\n2 1\\n11 10\\n\", \"1 0\\n8 7\\n1 1\\n\", \"2 1\\n2 1\\n1 1\\n\", \"1 1\\n1 0\\n11 10\\n\", \"1 1\\n5 4\\n1 1\\n\", \"9 8\\n2 1\\n2 1\\n\", \"20 19\\n1 1\\n1 0\\n\", \"1 1\\n4 3\\n1 0\\n\", \"2 1\\n11 10\\n1 1\\n\", \"1 1\\n23 22\\n2 1\\n\", \"1 1\\n1 0\\n4 3\\n\", \"1 1\\n1 1\\n4 3\\n\", \"4 3\\n28 27\\n8 7\\n\", \"10 9\\n1 0\\n1 1\\n\", \"8 7\\n1 1\\n1 1\\n\", \"1 1\\n53 52\\n1 1\\n\", \"1 1\\n1 1\\n5 4\\n\", \"1 1\\n46 45\\n1 1\\n\", \"4 3\\n3 2\\n1 1\\n\", \"3 2\\n2 1\\n1 1\\n\", \"6 5\\n1 1\\n1 1\\n\", \"1 1\\n1 0\\n1 1\"]}", "source": "taco"}
|
Problem statement
There are rectangles with vertical and horizontal lengths of h and w, and square squares with a side length of 1 are spread inside. If the upper left cell is (0,0) and the cell to the right of j below (0,0) is represented as (i, j), (i, j) is i + j. If is even, it is painted red, and if it is odd, it is painted blue.
Now, the upper left vertex of (0,0) and the lower right vertex of (h − 1, w − 1) are connected by a line segment. If the length of the red part through which this line segment passes is a and the length of the blue part is b, the ratio a: b is an integer ratio. Express a: b in the simplest way (with relatively prime integers).
input
T
h_1 \ w_1
...
h_T \ w_T
One file contains T inputs. The T in the first line and the vertical and horizontal lengths h_i and w_i in the Tth input are input in the 1 + i line.
Constraint
* An integer
* 1 ≤ T ≤ 1000
* 1 ≤ h_i, w_i ≤ 109
output
Output the answer for each case separated by 1 and separated by spaces. It spans T lines in total.
sample
Sample input 1
3
twenty three
3 3
4 3
Sample output 1
1 1
Ten
1 1
<image>
Example
Input
3
2 3
3 3
4 3
Output
1 1
1 0
1 1
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"2 1\", \"2 2\", \"2 4\", \"0 4\", \"-1 4\", \"-1 0\", \"1 -1\", \"-1 2\", \"-1 -4\", \"-2 -7\", \"-1 -7\", \"-1 -5\", \"1 -6\", \"2 -6\", \"2 -8\", \"5 -10\", \"5 -8\", \"9 -8\", \"9 -14\", \"9 -25\", \"9 -20\", \"18 -20\", \"18 -36\", \"18 -33\", \"18 -27\", \"33 -27\", \"33 -33\", \"66 -33\", \"66 -51\", \"66 -87\", \"66 -49\", \"96 -49\", \"96 -45\", \"96 -10\", \"96 -13\", \"96 -6\", \"96 -11\", \"96 -18\", \"96 -15\", \"96 -24\", \"86 -24\", \"86 -1\", \"86 -2\", \"86 -4\", \"86 -5\", \"86 -3\", \"67 -3\", \"56 -3\", \"56 -1\", \"18 -1\", \"18 0\", \"16 0\", \"12 -2\", \"12 0\", \"-8 0\", \"-13 0\", \"-13 -1\", \"-7 -1\", \"-8 -1\", \"-13 1\", \"-11 0\", \"-19 0\", \"-26 0\", \"-26 -1\", \"-39 -1\", \"-31 -1\", \"-20 0\", \"-28 -1\", \"-28 -4\", \"-8 1\", \"-1 9\", \"-1 14\", \"-2 16\", \"0 16\", \"1 24\", \"-1 38\", \"-1 60\", \"-1 33\", \"0 33\", \"1 33\", \"-2 33\", \"-2 -13\", \"-1 -31\", \"-1 -25\", \"0 -25\", \"1 -8\", \"21 1\", \"52 0\", \"84 0\", \"84 1\", \"49 1\", \"96 1\", \"116 0\", \"118 0\", \"118 -1\", \"3 -19\", \"3 -30\", \"-1 -43\", \"0 -43\", \"1 -54\", \"2 0\"], \"outputs\": [\"0\\n\", \"-1\\n\", \"-3\\n\", \"-5\\n\", \"-6\\n\", \"-2\\n\", \"1\\n\", \"-4\\n\", \"2\\n\", \"4\\n\", \"5\\n\", \"3\\n\", \"6\\n\", \"7\\n\", \"9\\n\", \"14\\n\", \"12\\n\", \"16\\n\", \"22\\n\", \"33\\n\", \"28\\n\", \"37\\n\", \"53\\n\", \"50\\n\", \"44\\n\", \"59\\n\", \"65\\n\", \"98\\n\", \"116\\n\", \"152\\n\", \"114\\n\", \"144\\n\", \"140\\n\", \"105\\n\", \"108\\n\", \"101\\n\", \"106\\n\", \"113\\n\", \"110\\n\", \"119\\n\", \"109\\n\", \"86\\n\", \"87\\n\", \"89\\n\", \"90\\n\", \"88\\n\", \"69\\n\", \"58\\n\", \"56\\n\", \"18\\n\", \"17\\n\", \"15\\n\", \"13\\n\", \"11\\n\", \"-9\\n\", \"-14\\n\", \"-13\\n\", \"-7\\n\", \"-8\\n\", \"-15\\n\", \"-12\\n\", \"-20\\n\", \"-27\\n\", \"-26\\n\", \"-39\\n\", \"-31\\n\", \"-21\\n\", \"-28\\n\", \"-25\\n\", \"-10\\n\", \"-11\\n\", \"-16\\n\", \"-19\\n\", \"-17\\n\", \"-24\\n\", \"-40\\n\", \"-62\\n\", \"-35\\n\", \"-34\\n\", \"-33\\n\", \"-36\\n\", \"10\\n\", \"29\\n\", \"23\\n\", \"24\\n\", \"8\\n\", \"19\\n\", \"51\\n\", \"83\\n\", \"82\\n\", \"47\\n\", \"94\\n\", \"115\\n\", \"117\\n\", \"118\\n\", \"21\\n\", \"32\\n\", \"41\\n\", \"42\\n\", \"54\\n\", \"1\"]}", "source": "taco"}
|
problem
AOR Ika and you came to the tournament-style table tennis tournament singles section for reconnaissance. For AOR Ika-chan, who wants to record all the games, you decide to ask for the number of games that will be played in this tournament.
There are $ N $ players in the tournament, each with a uniform number of $ 0, \ dots, N -1 $. Among them, $ M $ players abstained and did not participate in the match.
The number of games in this tournament will be determined based on the following rules.
* There are no seed players, and the number of wins required for any contestant to win is constant.
* If the opponent is absent, the match will not be played and the player who participated will win. It is not counted in the number of games.
* The tournament will end when the winner is decided.
* A person who loses a match will not play the match again. In other words, there will be no repechage or third place playoff.
* Since there is only one table tennis table, different games will not be played at the same time, and the winner will always be decided in each game (it will not be a draw).
The definition of the tournament is as follows. The tournament is represented by a full binary tree with a height of $ L = \ log_2 N $, and each apex of the leaf has the participant's uniform number written on it. Assuming that the root depth is 0, in the $ i $ round ($ 1 \ le i \ le L $), the players with the numbers written on the children of each vertex of the depth $ L --i $ will play a match. Write the winner's uniform number at the top.
<image>
output
Output the number of games played by the end of this tournament in one line. Also, output a line break at the end.
Example
Input
2 0
Output
1
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4 6\\n1 2 3 4 3 2\\n\", \"10 5\\n9 4 3 8 8\\n\", \"5 10\\n2 5 2 2 3 5 3 2 1 3\\n\", \"10 20\\n6 3 9 6 1 9 1 9 8 2 7 6 9 8 4 7 1 2 4 2\\n\", \"100 100\\n28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28\\n\", \"100000 1\\n97735\\n\", \"10 100\\n3 2 5 7 1 1 5 10 1 4 7 4 4 10 1 3 8 1 7 4 4 8 5 7 2 10 10 2 2 4 4 5 5 4 8 8 8 9 10 5 1 3 10 3 6 10 6 4 9 10 10 4 10 1 2 5 9 8 9 7 10 9 10 1 6 3 4 7 8 6 3 5 7 10 5 5 8 3 1 2 1 7 6 10 4 4 2 9 9 9 9 8 8 5 4 3 9 7 7 10\\n\", \"100000 1\\n14542\\n\", \"44 44\\n22 26 30 41 2 32 7 12 13 22 5 43 33 12 40 14 32 40 3 28 35 26 26 43 3 14 15 16 18 13 42 10 21 19 1 17 34 26 10 40 7 25 20 12\\n\", \"2 3\\n1 1 2\\n\", \"100000 50\\n43104 45692 17950 43454 99127 33540 80887 7990 116 79790 66870 61322 5479 24876 7182 99165 81535 3498 54340 7460 43666 921 1905 68827 79308 59965 8437 13422 40523 59605 39474 22019 65794 40905 35727 78900 41981 91502 66506 1031 92025 84135 19675 67950 81327 95915 92076 89843 43174 73177\\n\", \"100 100\\n11 41 76 12 57 12 31 68 92 52 63 40 71 18 69 21 15 27 80 72 69 43 67 37 21 98 36 100 39 93 24 98 6 72 37 33 60 4 38 52 92 60 21 39 65 60 57 87 68 34 23 72 45 13 7 55 81 61 61 49 10 89 52 63 12 21 75 2 69 38 71 35 80 41 1 57 22 60 50 60 40 83 22 70 84 40 61 14 65 93 41 96 51 19 21 36 96 97 12 69\\n\", \"1 1\\n1\\n\", \"11 5\\n1 1 1 10 11\\n\", \"100 6\\n1 1 3 3 1 1\\n\", \"100 14\\n1 2 100 100 100 100 100 100 100 100 100 100 2 1\\n\", \"1000 10\\n1 1 1 1 1 1000 1000 1000 1000 1000\\n\", \"3 6\\n1 1 1 3 3 3\\n\", \"10 4\\n7 1 1 8\\n\", \"3 18\\n1 1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 3\\n\", \"5 4\\n5 5 2 1\\n\", \"10 10\\n8 8 8 7 7 7 6 1 1 1\\n\", \"10 10\\n8 8 8 7 7 7 6 1 1 1\\n\", \"100000 50\\n43104 45692 17950 43454 99127 33540 80887 7990 116 79790 66870 61322 5479 24876 7182 99165 81535 3498 54340 7460 43666 921 1905 68827 79308 59965 8437 13422 40523 59605 39474 22019 65794 40905 35727 78900 41981 91502 66506 1031 92025 84135 19675 67950 81327 95915 92076 89843 43174 73177\\n\", \"1 1\\n1\\n\", \"100000 1\\n14542\\n\", \"10 4\\n7 1 1 8\\n\", \"11 5\\n1 1 1 10 11\\n\", \"10 20\\n6 3 9 6 1 9 1 9 8 2 7 6 9 8 4 7 1 2 4 2\\n\", \"100 100\\n28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28\\n\", \"1000 10\\n1 1 1 1 1 1000 1000 1000 1000 1000\\n\", \"3 18\\n1 1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 3\\n\", \"5 10\\n2 5 2 2 3 5 3 2 1 3\\n\", \"3 6\\n1 1 1 3 3 3\\n\", \"44 44\\n22 26 30 41 2 32 7 12 13 22 5 43 33 12 40 14 32 40 3 28 35 26 26 43 3 14 15 16 18 13 42 10 21 19 1 17 34 26 10 40 7 25 20 12\\n\", \"100 100\\n11 41 76 12 57 12 31 68 92 52 63 40 71 18 69 21 15 27 80 72 69 43 67 37 21 98 36 100 39 93 24 98 6 72 37 33 60 4 38 52 92 60 21 39 65 60 57 87 68 34 23 72 45 13 7 55 81 61 61 49 10 89 52 63 12 21 75 2 69 38 71 35 80 41 1 57 22 60 50 60 40 83 22 70 84 40 61 14 65 93 41 96 51 19 21 36 96 97 12 69\\n\", \"100000 1\\n97735\\n\", \"100 14\\n1 2 100 100 100 100 100 100 100 100 100 100 2 1\\n\", \"100 6\\n1 1 3 3 1 1\\n\", \"10 100\\n3 2 5 7 1 1 5 10 1 4 7 4 4 10 1 3 8 1 7 4 4 8 5 7 2 10 10 2 2 4 4 5 5 4 8 8 8 9 10 5 1 3 10 3 6 10 6 4 9 10 10 4 10 1 2 5 9 8 9 7 10 9 10 1 6 3 4 7 8 6 3 5 7 10 5 5 8 3 1 2 1 7 6 10 4 4 2 9 9 9 9 8 8 5 4 3 9 7 7 10\\n\", \"2 3\\n1 1 2\\n\", \"5 4\\n5 5 2 1\\n\", \"100000 1\\n7122\\n\", \"11 5\\n1 1 1 10 6\\n\", \"10 20\\n6 3 9 8 1 9 1 9 8 2 7 6 9 8 4 7 1 2 4 2\\n\", \"3 18\\n1 1 1 2 1 1 1 1 1 3 3 3 3 3 3 3 3 3\\n\", \"44 44\\n22 26 30 41 2 32 7 12 13 22 5 43 33 12 40 14 32 40 3 28 16 26 26 43 3 14 15 16 18 13 42 10 21 19 1 17 34 26 10 40 7 25 20 12\\n\", \"100 100\\n11 41 76 12 57 12 31 68 92 52 63 40 71 18 69 21 15 27 80 72 69 43 67 37 21 98 36 100 39 93 24 98 6 72 37 38 60 4 38 52 92 60 21 39 65 60 57 87 68 34 23 72 45 13 7 55 81 61 61 49 10 89 52 63 12 21 75 2 69 38 71 35 80 41 1 57 22 60 50 60 40 83 22 70 84 40 61 14 65 93 41 96 51 19 21 36 96 97 12 69\\n\", \"101 14\\n1 2 100 100 100 100 100 100 100 100 100 100 2 1\\n\", \"10 100\\n3 2 5 7 1 1 5 10 1 4 7 4 4 10 1 3 8 1 7 4 4 8 5 7 2 10 10 2 2 4 4 5 5 4 8 8 8 9 10 5 1 3 10 3 6 10 6 4 9 10 10 4 10 1 2 5 9 8 9 7 10 9 10 1 6 3 4 7 8 6 6 5 7 10 5 5 8 3 1 2 1 7 6 10 4 4 2 9 9 9 9 8 8 5 4 3 9 7 7 10\\n\", \"11 5\\n2 1 1 10 6\\n\", \"10 20\\n6 3 9 8 1 9 1 9 8 2 7 6 9 8 4 7 1 1 4 2\\n\", \"44 44\\n22 37 30 41 2 32 7 12 13 22 5 43 33 12 40 14 32 40 3 28 16 26 26 43 3 14 15 16 18 13 42 10 21 19 1 17 34 26 10 40 7 25 20 12\\n\", \"10 20\\n6 3 9 8 1 9 1 9 8 2 7 6 9 8 4 7 2 1 4 2\\n\", \"100 100\\n28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 32 28 30 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 1 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28\\n\", \"10 20\\n6 3 9 8 1 9 1 6 8 2 7 6 9 8 4 7 2 1 4 2\\n\", \"44 44\\n22 37 30 41 2 32 7 12 13 22 5 43 4 12 40 14 32 40 3 28 16 26 26 43 3 14 15 18 18 13 42 10 21 19 1 17 34 26 10 40 7 25 20 12\\n\", \"44 44\\n22 37 30 41 2 32 7 12 13 22 5 43 4 12 40 14 32 40 3 28 16 26 26 43 3 14 15 18 22 13 42 10 21 19 1 17 34 26 10 40 7 25 20 12\\n\", \"10 4\\n7 1 2 8\\n\", \"11 5\\n1 1 2 10 11\\n\", \"10 20\\n6 3 9 6 2 9 1 9 8 2 7 6 9 8 4 7 1 2 4 2\\n\", \"100 100\\n11 41 76 12 57 12 31 68 92 52 63 40 71 18 69 21 15 27 80 72 69 43 67 37 21 98 36 100 39 93 24 98 6 72 37 33 60 4 38 52 92 60 21 19 65 60 57 87 68 34 23 72 45 13 7 55 81 61 61 49 10 89 52 63 12 21 75 2 69 38 71 35 80 41 1 57 22 60 50 60 40 83 22 70 84 40 61 14 65 93 41 96 51 19 21 36 96 97 12 69\\n\", \"10 100\\n3 2 5 7 1 1 5 10 1 4 7 4 4 10 1 3 8 1 7 4 4 8 5 7 2 10 10 2 2 4 4 5 5 4 8 8 8 9 10 5 1 1 10 3 6 10 6 4 9 10 10 4 10 1 2 5 9 8 9 7 10 9 10 1 6 3 4 7 8 6 3 5 7 10 5 5 8 3 1 2 1 7 6 10 4 4 2 9 9 9 9 8 8 5 4 3 9 7 7 10\\n\", \"4 6\\n1 2 4 4 3 2\\n\", \"100 100\\n28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 30 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28\\n\", \"100000 1\\n41165\\n\", \"100 6\\n1 1 3 4 1 1\\n\", \"100000 1\\n5459\\n\", \"100 100\\n28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 30 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 1 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28\\n\", \"10 100\\n3 2 5 7 1 1 5 10 1 4 7 4 4 10 1 3 8 1 7 4 4 8 5 7 2 10 10 2 2 4 4 5 5 4 8 8 8 9 10 5 1 3 10 3 6 10 6 4 9 10 10 4 10 1 2 5 9 8 9 7 10 9 10 1 6 3 4 7 8 6 6 5 7 10 5 5 8 3 1 2 1 7 6 10 4 4 2 9 9 9 8 8 8 5 4 3 9 7 7 10\\n\", \"100000 1\\n3514\\n\", \"11 5\\n2 2 1 10 6\\n\", \"44 44\\n22 37 30 41 2 32 7 12 13 22 5 43 33 12 40 14 32 40 3 28 16 26 26 43 3 14 15 18 18 13 42 10 21 19 1 17 34 26 10 40 7 25 20 12\\n\", \"100000 1\\n6116\\n\", \"100 100\\n28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 32 28 30 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 1 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 7 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28\\n\", \"100000 1\\n465\\n\", \"100001 1\\n465\\n\", \"44 44\\n22 37 30 41 2 32 7 12 13 22 5 43 4 12 40 14 32 40 3 28 16 26 26 43 3 9 15 18 22 13 42 10 21 19 1 17 34 26 10 40 7 25 20 12\\n\", \"100000 1\\n14270\\n\", \"100 100\\n28 28 28 28 28 28 28 28 28 28 28 51 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28\\n\", \"3 18\\n1 1 1 1 1 1 1 1 1 3 3 3 3 3 1 3 3 3\\n\", \"5 10\\n2 5 4 2 3 5 3 2 1 3\\n\", \"3 6\\n1 1 1 3 1 3\\n\", \"44 44\\n22 26 30 41 2 32 7 12 13 22 5 43 33 12 40 14 32 40 3 28 1 26 26 43 3 14 15 16 18 13 42 10 21 19 1 17 34 26 10 40 7 25 20 12\\n\", \"2 3\\n2 1 2\\n\", \"10 5\\n9 4 3 2 8\\n\", \"10 20\\n6 5 9 8 1 9 1 9 8 2 7 6 9 8 4 7 1 2 4 2\\n\", \"10 5\\n9 4 3 8 8\\n\", \"4 6\\n1 2 3 4 3 2\\n\"], \"outputs\": [\"3\\n\", \"6\\n\", \"7\\n\", \"52\\n\", \"0\\n\", \"0\\n\", \"218\\n\", \"0\\n\", \"568\\n\", \"0\\n\", \"1583927\\n\", \"3302\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \" 2\\n\", \" 1583927\\n\", \" 0\\n\", \" 0\\n\", \" 1\\n\", \" 1\\n\", \" 52\\n\", \" 0\\n\", \" 0\\n\", \" 0\\n\", \" 7\\n\", \" 0\\n\", \" 568\\n\", \" 3302\\n\", \" 0\\n\", \" 2\\n\", \" 0\\n\", \" 218\\n\", \" 0\\n\", \" 1\\n\", \"0\\n\", \"4\\n\", \"48\\n\", \"1\\n\", \"574\\n\", \"3294\\n\", \"2\\n\", \"214\\n\", \"6\\n\", \"44\\n\", \"588\\n\", \"54\\n\", \"12\\n\", \"56\\n\", \"604\\n\", \"612\\n\", \"7\\n\", \"9\\n\", \"58\\n\", \"3306\\n\", \"218\\n\", \"3\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"4\\n\", \"214\\n\", \"0\\n\", \"6\\n\", \"588\\n\", \"0\\n\", \"54\\n\", \"0\\n\", \"0\\n\", \"612\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"9\\n\", \"0\\n\", \"604\\n\", \"0\\n\", \"7\\n\", \"44\\n\", \" 6\\n\", \" 3\\n\"]}", "source": "taco"}
|
Ryouko is an extremely forgetful girl, she could even forget something that has just happened. So in order to remember, she takes a notebook with her, called Ryouko's Memory Note. She writes what she sees and what she hears on the notebook, and the notebook became her memory.
Though Ryouko is forgetful, she is also born with superb analyzing abilities. However, analyzing depends greatly on gathered information, in other words, memory. So she has to shuffle through her notebook whenever she needs to analyze, which is tough work.
Ryouko's notebook consists of n pages, numbered from 1 to n. To make life (and this problem) easier, we consider that to turn from page x to page y, |x - y| pages should be turned. During analyzing, Ryouko needs m pieces of information, the i-th piece of information is on page a_{i}. Information must be read from the notebook in order, so the total number of pages that Ryouko needs to turn is $\sum_{i = 1}^{m - 1}|a_{i + 1} - a_{i}|$.
Ryouko wants to decrease the number of pages that need to be turned. In order to achieve this, she can merge two pages of her notebook. If Ryouko merges page x to page y, she would copy all the information on page x to y (1 ≤ x, y ≤ n), and consequently, all elements in sequence a that was x would become y. Note that x can be equal to y, in which case no changes take place.
Please tell Ryouko the minimum number of pages that she needs to turn. Note she can apply the described operation at most once before the reading. Note that the answer can exceed 32-bit integers.
-----Input-----
The first line of input contains two integers n and m (1 ≤ n, m ≤ 10^5).
The next line contains m integers separated by spaces: a_1, a_2, ..., a_{m} (1 ≤ a_{i} ≤ n).
-----Output-----
Print a single integer — the minimum number of pages Ryouko needs to turn.
-----Examples-----
Input
4 6
1 2 3 4 3 2
Output
3
Input
10 5
9 4 3 8 8
Output
6
-----Note-----
In the first sample, the optimal solution is to merge page 4 to 3, after merging sequence a becomes {1, 2, 3, 3, 3, 2}, so the number of pages Ryouko needs to turn is |1 - 2| + |2 - 3| + |3 - 3| + |3 - 3| + |3 - 2| = 3.
In the second sample, optimal solution is achieved by merging page 9 to 4.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [[1], [2], [3], [4], [12], [13], [100], [110]], \"outputs\": [[1], [5], [6], [25], [2890625], [7109376], [6188999442576576769103890995893380022607743740081787109376], [9580863811000557423423230896109004106619977392256259918212890625]]}", "source": "taco"}
|
This is a very simply formulated task. Let's call an integer number `N` 'green' if `N²` ends with all of the digits of `N`. Some examples:
`5` is green, because `5² = 25` and `25` ends with `5`.
`11` is not green, because `11² = 121` and `121` does not end with `11`.
`376` is green, because `376² = 141376` and `141376` ends with `376`.
Your task is to write a function `green` that returns `n`th green number, starting with `1` - `green (1) == 1`
---
## Data range
```if:haskell
`n <= 4000` for Haskell
```
```if:java
`n <= 5000` for Java
```
```if:python
`n <= 5000` for Python
```
```if:javascript
`n <= 3000` for JavaScript
Return values should be `String`s, and should be exact. A BigNum library is recommended.
```
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[7.4, 10215, 24, 20], [7.9, 107090, 48, 41], [6.8, 105097, 36, 4], [3.8, 48603, 24, 10], [1.9, 182840, 48, 18], [1.9, 19121, 48, 2], [2.2, 112630, 60, 11], [5.6, 133555, 60, 53], [9.8, 67932, 60, 34], [3.7, 64760, 36, 24], [4.6, 85591, 36, 5], [7.0, 168742, 48, 16], [9.6, 17897, 60, 23], [5.2, 53521, 60, 51], [6.8, 139308, 60, 38], [5.0, 182075, 24, 9], [8.0, 128263, 36, 26], [7.8, 112414, 60, 37], [4.9, 93221, 36, 5], [1.2, 146157, 48, 20], [3.6, 168849, 24, 11], [9.3, 87820, 60, 14], [8.7, 155744, 36, 31], [6.4, 179023, 36, 11], [8.3, 38495, 36, 15], [9.6, 150614, 24, 19], [2.5, 159363, 48, 19], [4.7, 56245, 48, 11], [1.5, 142777, 36, 32], [9.6, 187340, 60, 28], [2.4, 57707, 24, 14], [3.0, 180678, 36, 31], [2.0, 139586, 24, 13], [5.3, 142498, 60, 46], [9.0, 150309, 48, 29], [7.1, 60232, 60, 56], [8.7, 172214, 36, 14], [9.0, 187174, 60, 12], [9.5, 119722, 60, 23], [9.2, 10536, 36, 15], [1.9, 70139, 24, 13], [4.5, 141454, 36, 23], [4.5, 154486, 24, 7], [2.2, 20254, 36, 35], [3.7, 114512, 36, 23], [8.6, 121685, 48, 24], [1.1, 171542, 48, 25], [1.1, 121991, 48, 20], [8.9, 162862, 60, 46], [1.9, 152921, 60, 19]], \"outputs\": [[\"num_payment 20 c 459 princ 445 int 14 balance 1809\"], [\"num_payment 41 c 2609 princ 2476 int 133 balance 17794\"], [\"num_payment 4 c 3235 princ 2685 int 550 balance 94447\"], [\"num_payment 10 c 2106 princ 2009 int 98 balance 28799\"], [\"num_payment 18 c 3959 princ 3769 int 189 balance 115897\"], [\"num_payment 2 c 414 princ 384 int 30 balance 18353\"], [\"num_payment 11 c 1984 princ 1810 int 174 balance 92897\"], [\"num_payment 53 c 2557 princ 2464 int 93 balance 17571\"], [\"num_payment 34 c 1437 princ 1153 int 283 balance 33532\"], [\"num_payment 24 c 1903 princ 1829 int 75 balance 22389\"], [\"num_payment 5 c 2550 princ 2256 int 294 balance 74397\"], [\"num_payment 16 c 4041 princ 3335 int 706 balance 117641\"], [\"num_payment 23 c 377 princ 278 int 98 balance 12025\"], [\"num_payment 51 c 1015 princ 972 int 43 balance 8939\"], [\"num_payment 38 c 2745 princ 2411 int 335 balance 56634\"], [\"num_payment 9 c 7988 princ 7474 int 514 balance 115917\"], [\"num_payment 26 c 4019 princ 3736 int 283 balance 38758\"], [\"num_payment 37 c 2269 princ 1942 int 327 balance 48320\"], [\"num_payment 5 c 2790 princ 2449 int 341 balance 81077\"], [\"num_payment 20 c 3120 princ 3031 int 89 balance 86109\"], [\"num_payment 11 c 7302 princ 7002 int 300 balance 92965\"], [\"num_payment 14 c 1836 princ 1277 int 559 balance 70807\"], [\"num_payment 31 c 4931 princ 4722 int 209 balance 24127\"], [\"num_payment 11 c 5479 princ 4771 int 708 balance 127911\"], [\"num_payment 15 c 1212 princ 1041 int 170 balance 23607\"], [\"num_payment 19 c 6922 princ 6599 int 323 balance 33796\"], [\"num_payment 19 c 3492 princ 3281 int 211 balance 98178\"], [\"num_payment 11 c 1288 princ 1110 int 178 balance 44271\"], [\"num_payment 32 c 4058 princ 4033 int 25 balance 16183\"], [\"num_payment 28 c 3944 princ 3032 int 912 balance 110949\"], [\"num_payment 14 c 2465 princ 2411 int 54 balance 24381\"], [\"num_payment 31 c 5254 princ 5176 int 78 balance 26076\"], [\"num_payment 13 c 5938 princ 5821 int 117 balance 64670\"], [\"num_payment 46 c 2709 princ 2535 int 173 balance 36695\"], [\"num_payment 29 c 3740 princ 3221 int 519 balance 66007\"], [\"num_payment 56 c 1196 princ 1161 int 35 balance 4712\"], [\"num_payment 14 c 5452 princ 4618 int 835 balance 110505\"], [\"num_payment 12 c 3885 princ 2694 int 1191 balance 156135\"], [\"num_payment 23 c 2514 princ 1863 int 651 balance 80372\"], [\"num_payment 15 c 336 princ 284 int 52 balance 6495\"], [\"num_payment 13 c 2981 princ 2925 int 56 balance 32478\"], [\"num_payment 23 c 4208 princ 3993 int 215 balance 53292\"], [\"num_payment 7 c 6743 princ 6304 int 439 balance 110852\"], [\"num_payment 35 c 582 princ 580 int 2 balance 581\"], [\"num_payment 23 c 3366 princ 3224 int 142 balance 42823\"], [\"num_payment 24 c 3005 princ 2514 int 491 balance 66044\"], [\"num_payment 25 c 3655 princ 3575 int 79 balance 83139\"], [\"num_payment 20 c 2599 princ 2531 int 68 balance 71813\"], [\"num_payment 46 c 3373 princ 3019 int 354 balance 44694\"], [\"num_payment 19 c 2674 princ 2502 int 172 balance 106057\"]]}", "source": "taco"}
|
The description is rather long but it tries to explain what a financing plan is.
The fixed monthly payment for a fixed rate mortgage is the amount paid by the borrower every month that ensures
that the loan is paid off in full with interest at the end of its term.
The monthly payment formula is based on the annuity formula.
The monthly payment `c` depends upon:
- `rate` - the monthly interest rate is expressed as a decimal, not a percentage.
The monthly rate is simply the **given** yearly percentage rate divided by 100 and then by 12.
- `term` - the number of monthly payments, called the loan's `term`.
- `principal` - the amount borrowed, known as the loan's principal (or `balance`).
First we have to determine `c`.
We have: `c = n /d` with `n = r * balance` and `d = 1 - (1 + r)**(-term)` where `**` is the `power` function (you can look at the reference below).
The payment `c` is composed of two parts. The first part pays the interest (let us call it `int`)
due for the balance of the given month, the second part repays the balance (let us call this part `princ`) hence for the following month we get a `new balance = old balance - princ` with `c = int + princ`.
Loans are structured so that the amount of principal returned to the borrower starts out small and increases with each mortgage payment.
While the mortgage payments in the first years consist primarily of interest payments, the payments in the final years consist primarily of principal repayment.
A mortgage's amortization schedule provides a detailed look at precisely what portion of each mortgage payment is dedicated to each component.
In an example of a $100,000, 30-year mortgage with a rate of 6 percents the amortization schedule consists of 360 monthly payments.
The partial amortization schedule below shows with 2 decimal floats
the balance between principal and interest payments.
--|num_payment|c |princ |int |Balance |
--|-----------|-----------|-----------|-----------|-----------|
--|1 |599.55 |99.55 |500.00 |99900.45 |
--|... |599.55 |... |... |... |
--|12 |599.55 |105.16 |494.39 |98,771.99 |
--|... |599.55 |... |... |... |
--|360 |599.55 |596.57 |2.98 |0.00 |
# Task:
Given parameters
```
rate: annual rate as percent (don't forgent to divide by 100*12)
bal: original balance (borrowed amount)
term: number of monthly payments
num_payment: rank of considered month (from 1 to term)
```
the function `amort` will return a formatted string:
`"num_payment %d c %.0f princ %.0f int %.0f balance %.0f" (with arguments num_payment, c, princ, int, balance`)
# Examples:
```
amort(6, 100000, 360, 1) ->
"num_payment 1 c 600 princ 100 int 500 balance 99900"
amort(6, 100000, 360, 12) ->
"num_payment 12 c 600 princ 105 int 494 balance 98772"
```
# Ref
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n0\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n101\\n0\\n2\\n00000\\n10001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n0\\n101\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n011\\n111\\n0\\n2\\n00000\\n00001\\n4\\n0\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0010\\n0110\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n10001\\n4\\n01\\n001\\n1001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n011\\n111\\n0\\n2\\n00000\\n00001\\n4\\n0\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0010\\n0110\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0010\\n0110\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0110\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0110\\n3\\n011\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n000\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0010\\n0110\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n1\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0110\\n3\\n010\\n111\\n0\\n2\\n00000\\n00101\\n4\\n0\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n01000\\n00001\\n2\\n0\\n001\\n0011\\n00001\\n\", \"4\\n4\\n1001\\n0000\\n0010\\n0110\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n1\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n0\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n01001\\n\", \"4\\n4\\n0001\\n0010\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n0\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0101\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0110\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n01001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n10001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n00000\\n00001\\n4\\n0\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n000\\n111\\n0\\n2\\n00000\\n10001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0110\\n3\\n011\\n111\\n0\\n2\\n00010\\n00001\\n4\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0110\\n3\\n011\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n00000\\n00001\\n4\\n01\\n000\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00101\\n4\\n0\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n110\\n1\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n0\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00010\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n000\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n101\\n0\\n2\\n00000\\n11001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n1001\\n0010\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n1101\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n00101\\n4\\n01\\n001\\n0011\\n01001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n011\\n111\\n0\\n2\\n00000\\n00101\\n4\\n0\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n01000\\n00001\\n4\\n0\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n011\\n111\\n0\\n2\\n10000\\n00001\\n4\\n0\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0110\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0110\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n1011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0110\\n3\\n011\\n111\\n0\\n2\\n00000\\n00001\\n3\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0110\\n3\\n011\\n111\\n0\\n2\\n00010\\n00001\\n4\\n01\\n001\\n0001\\n00000\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00100\\n00001\\n4\\n01\\n000\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n10000\\n00001\\n4\\n01\\n000\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n110\\n1\\n2\\n00010\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n110\\n111\\n0\\n2\\n00000\\n00001\\n4\\n0\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n100\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n000\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n000\\n101\\n0\\n2\\n00000\\n11001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n1001\\n0010\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n00000\\n00011\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0100\\n0011\\n1101\\n3\\n010\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00000\\n01101\\n4\\n01\\n001\\n0011\\n01001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n011\\n111\\n0\\n2\\n00000\\n00101\\n4\\n0\\n011\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n011\\n111\\n0\\n2\\n10000\\n00001\\n4\\n0\\n001\\n0001\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n011\\n111\\n0\\n2\\n00000\\n00001\\n3\\n01\\n001\\n0011\\n00000\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0100\\n3\\n011\\n111\\n0\\n2\\n00010\\n00001\\n4\\n01\\n001\\n0001\\n00000\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n0\\n2\\n00100\\n00011\\n4\\n01\\n000\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n111\\n1\\n2\\n10000\\n00001\\n4\\n01\\n000\\n0001\\n10001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0110\\n3\\n010\\n111\\n0\\n2\\n00000\\n00101\\n1\\n0\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n010\\n010\\n1\\n2\\n00010\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0111\\n3\\n110\\n111\\n0\\n2\\n01000\\n00001\\n4\\n0\\n001\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n0000\\n0011\\n0101\\n3\\n100\\n111\\n0\\n2\\n00000\\n00001\\n4\\n01\\n000\\n0011\\n00001\\n\", \"4\\n4\\n0001\\n1000\\n0011\\n0111\\n3\\n010\\n101\\n0\\n2\\n00000\\n00001\\n4\\n01\\n001\\n0001\\n00001\\n\"], \"outputs\": [\"1\\n3\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n-1\\n2\\n1 2\\n\", \"1\\n3\\n0\\n\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n3\\n\", \"1\\n3\\n0\\n\\n0\\n\\n1\\n2\\n\", \"0\\n\\n0\\n\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n-1\\n1\\n1\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n2\\n\", \"0\\n\\n0\\n\\n0\\n\\n1\\n1\\n\", \"0\\n\\n-1\\n0\\n\\n1\\n1\\n\", \"1\\n1\\n-1\\n0\\n\\n1\\n1\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n1\\n\", \"0\\n\\n-1\\n0\\n\\n0\\n\\n\", \"0\\n\\n-1\\n0\\n\\n1\\n2\\n\", \"1\\n3\\n-1\\n0\\n\\n0\\n\\n\", \"-1\\n-1\\n0\\n\\n0\\n\\n\", \"1\\n3\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n2\\n\", \"1\\n3\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n-1\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n2\\n\", \"1\\n3\\n-1\\n-1\\n2\\n1 2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n1\\n0\\n\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n1\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n0\\n\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n3\\n-1\\n-1\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n0\\n\\n0\\n\\n1\\n2\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n1\\n-1\\n0\\n\\n1\\n1\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n1\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n1\\n\", \"1\\n1\\n0\\n\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n3\\n-1\\n-1\\n2\\n1 2\\n\", \"1\\n3\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n3\\n0\\n\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n1\\n\", \"1\\n3\\n-1\\n0\\n\\n1\\n1\\n\", \"0\\n\\n-1\\n0\\n\\n0\\n\\n\", \"1\\n1\\n-1\\n0\\n\\n2\\n1 2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n2\\n\", \"1\\n1\\n0\\n\\n0\\n\\n1\\n1\\n\", \"1\\n3\\n-1\\n0\\n\\n2\\n1 2\\n\"]}", "source": "taco"}
|
Polycarp has n different binary words. A word called binary if it contains only characters '0' and '1'. For example, these words are binary: "0001", "11", "0" and "0011100".
Polycarp wants to offer his set of n binary words to play a game "words". In this game, players name words and each next word (starting from the second) must start with the last character of the previous word. The first word can be any. For example, these sequence of words can be named during the game: "0101", "1", "10", "00", "00001".
Word reversal is the operation of reversing the order of the characters. For example, the word "0111" after the reversal becomes "1110", the word "11010" after the reversal becomes "01011".
Probably, Polycarp has such a set of words that there is no way to put them in the order correspondent to the game rules. In this situation, he wants to reverse some words from his set so that:
* the final set of n words still contains different words (i.e. all words are unique);
* there is a way to put all words of the final set of words in the order so that the final sequence of n words is consistent with the game rules.
Polycarp wants to reverse minimal number of words. Please, help him.
Input
The first line of the input contains one integer t (1 ≤ t ≤ 10^4) — the number of test cases in the input. Then t test cases follow.
The first line of a test case contains one integer n (1 ≤ n ≤ 2⋅10^5) — the number of words in the Polycarp's set. Next n lines contain these words. All of n words aren't empty and contains only characters '0' and '1'. The sum of word lengths doesn't exceed 4⋅10^6. All words are different.
Guaranteed, that the sum of n for all test cases in the input doesn't exceed 2⋅10^5. Also, guaranteed that the sum of word lengths for all test cases in the input doesn't exceed 4⋅10^6.
Output
Print answer for all of t test cases in the order they appear.
If there is no answer for the test case, print -1. Otherwise, the first line of the output should contain k (0 ≤ k ≤ n) — the minimal number of words in the set which should be reversed. The second line of the output should contain k distinct integers — the indexes of the words in the set which should be reversed. Words are numerated from 1 to n in the order they appear. If k=0 you can skip this line (or you can print an empty line). If there are many answers you can print any of them.
Example
Input
4
4
0001
1000
0011
0111
3
010
101
0
2
00000
00001
4
01
001
0001
00001
Output
1
3
-1
0
2
1 2
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[[1]], [[3, 5]], [[3, 9, 4]], [[5, 6, 7, 8]], [[13, 1, 21, 9]], [[13, 76, 21, 42, 63]]], \"outputs\": [[1], [8], [25], [52], [88], [674]]}", "source": "taco"}
|
## Number pyramid
Number pyramid is a recursive structure where each next row is constructed by adding adjacent values of the current row. For example:
```
Row 1 [1 2 3 4]
Row 2 [3 5 7]
Row 3 [8 12]
Row 4 [20]
```
___
## Task
Given the first row of the number pyramid, find the value stored in its last row.
___
## Examples
```python
reduce_pyramid([1]) == 1
reduce_pyramid([3, 5]) == 8
reduce_pyramid([3, 9, 4]) == 25
```
___
## Performance tests
```python
Number of tests: 10
List size: 10,000
```
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"8 3\\naeabcaez\\n\", \"8 3\\nabcddcbb\\n\", \"4 4\\nrkoa\\n\", \"39 30\\nyehuqwaffoiyxhkmdipxroolhahbhzprioobxfy\\n\", \"40 23\\nvwjzsgpdsopsrpsyccavfkyyahdgkmdxrquhcplw\\n\", \"10 5\\nabcdeedcba\\n\", \"5 5\\npjfjb\\n\", \"57 9\\nibkypcbtpdlhhpmghwrmuwaqoqxxexxqoqawumrwhgmphhldixezvfpqh\\n\", \"10 6\\nabcdefdcba\\n\", \"167 152\\nvqgjxbuxevpqbpnuyxktgpwdgyebnmrxbnitphshuloyykpgxakxadtguqskmhejndzptproeabnlvfwdyjiydfrjkxpvpbzwutsdpfawwcqqqirxwlkrectlnpdeccaoqetcaqcvyjtfoekyupvbsoiyldggycphddecbf\\n\", \"93 61\\nuecrsqsoylbotwcujcsbjohlyjlpjsjsnvttpytrvztqtkpsdcrvsossimwmglumwzpouhaiqvowthzsyonxjjearhniq\\n\", \"63 4\\nwzxjoumbtneztzheqznngprtcqjvawcycwavjqctrpgnnzqehztzentbmuojxzw\\n\", \"85 19\\nblkimwzicvbdkwfodvigvmnujnotwuobkjvugbtaseebxvdiorffqnhllwtwdnfodkuvdofwkdbvcizwmiklb\\n\", \"198 3\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqptqnflqqspvqrnmvucnspexpijnivqpavqxjyucufcullevaedlvut\\n\", \"46 29\\nxxzkzsxlyhotmfjpptrilatgtqpyshraiycmyzzlrcllvu\\n\", \"1 1\\na\\n\", \"2 2\\nat\\n\", \"10 4\\nabcddddcef\\n\", \"8 8\\naccedcba\\n\", \"1 1\\nd\\n\", \"5 5\\npjfjb\\n\", \"10 5\\nabcdeedcba\\n\", \"1 1\\nd\\n\", \"2 2\\nat\\n\", \"4 4\\nrkoa\\n\", \"10 4\\nabcddddcef\\n\", \"46 29\\nxxzkzsxlyhotmfjpptrilatgtqpyshraiycmyzzlrcllvu\\n\", \"198 3\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqptqnflqqspvqrnmvucnspexpijnivqpavqxjyucufcullevaedlvut\\n\", \"10 6\\nabcdefdcba\\n\", \"8 3\\nabcddcbb\\n\", \"85 19\\nblkimwzicvbdkwfodvigvmnujnotwuobkjvugbtaseebxvdiorffqnhllwtwdnfodkuvdofwkdbvcizwmiklb\\n\", \"167 152\\nvqgjxbuxevpqbpnuyxktgpwdgyebnmrxbnitphshuloyykpgxakxadtguqskmhejndzptproeabnlvfwdyjiydfrjkxpvpbzwutsdpfawwcqqqirxwlkrectlnpdeccaoqetcaqcvyjtfoekyupvbsoiyldggycphddecbf\\n\", \"63 4\\nwzxjoumbtneztzheqznngprtcqjvawcycwavjqctrpgnnzqehztzentbmuojxzw\\n\", \"93 61\\nuecrsqsoylbotwcujcsbjohlyjlpjsjsnvttpytrvztqtkpsdcrvsossimwmglumwzpouhaiqvowthzsyonxjjearhniq\\n\", \"1 1\\na\\n\", \"8 8\\naccedcba\\n\", \"57 9\\nibkypcbtpdlhhpmghwrmuwaqoqxxexxqoqawumrwhgmphhldixezvfpqh\\n\", \"40 23\\nvwjzsgpdsopsrpsyccavfkyyahdgkmdxrquhcplw\\n\", \"39 30\\nyehuqwaffoiyxhkmdipxroolhahbhzprioobxfy\\n\", \"2 2\\nau\\n\", \"198 3\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"167 59\\nvqgjxbuxevpqbpnuyxktgpwdgyebnmrxbnitphshuloyykpgxakxadtguqskmhejndzptproeabnlvfwdyjiydfrjkxpvpbzwutsdpfawwcqqqirxwlkrectlnpdeccaoqetcaqcvyjtfoekyupvbsoiyldggycphddecbf\\n\", \"8 8\\nacbedcca\\n\", \"8 3\\naeabcbez\\n\", \"198 4\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"167 37\\nvqgjxbuxevpqbpnuyxktgpwdgyebnmrxbnitphshuloyykpgxakxadtguqskmhejndzptproeabnlvfwdyjiydfrjkxpvpbzwutsdpfawwcqqqirxwlkrectlnpdeccaoqetcaqcvyjtfoekyupvbsoiyldggycphddecbf\\n\", \"5 1\\npjfjb\\n\", \"4 4\\nraok\\n\", \"46 32\\nxxzkzsxlyhotmfjpptrilatgtqpyshraiycmyzzlrcllvu\\n\", \"85 19\\nblkimwzicvbdkwfodvukdofndwtwllhnqffroidvxbeesatbguvjkbouwtonjunmvgivdofwkdbvcizwmiklb\\n\", \"167 152\\nfbceddhpcyggdlyiosbvpuykeoftjyvcqacteqoaccedpnltcerklwxriqqqcwwafpdstuwzbpvpxkjrfdyijydwfvlnbaeorptpzdnjehmksqugtdaxkaxgpkyyoluhshptinbxrmnbeygdwpgtkxyunpbqpvexubxjgqv\\n\", \"93 38\\nuecrsqsoylbotwcujcsbjohlyjlpjsjsnvttpytrvztqtkpsdcrvsossimwmglumwzpouhaiqvowthzsyonxjjearhniq\\n\", \"40 23\\nvwjzsgpdsosprpsyccavfkyyahdgkmdxrquhcplw\\n\", \"198 6\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"167 22\\nvqgjxbuxevpqbpnuyxktgpwdgyebnmrxbnitphshuloyykpgxakxadtguqskmhejndzptproeabnlvfwdyjiydfrjkxpvpbzwutsdpfawwcqqqirxwlkrectlnpdeccaoqetcaqcvyjtfoekyupvbsoiyldggycphddecbf\\n\", \"198 10\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"4 4\\nkrao\\n\", \"198 14\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"198 26\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"198 8\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"1 1\\ne\\n\", \"10 4\\ncbaddddcef\\n\", \"93 61\\nuecrsqsoylbotwcujcsbjohlyjlpjsjsnvttpytrvztqtkpsdcrvsossimwmglumwzpouhaiqvowthzsyonwjjearhniq\\n\", \"57 9\\nibkypcbtpdlhhpmghwrmuwaqoqxxexxqoqawumrwhgmphhldixezufpqh\\n\", \"46 32\\nxxzkzsxlyhotmfjpptrilatgtqpzshraiycmyzzlrcllvu\\n\", \"167 3\\nfbceddhpcyggdlyiosbvpuykeoftjyvcqacteqoaccedpnltcerklwxriqqqcwwafpdstuwzbpvpxkjrfdyijydwfvlnbaeorptpzdnjehmksqugtdaxkaxgpkyyoluhshptinbxrmnbeygdwpgtkxyunpbqpvexubxjgqv\\n\", \"198 6\\ntuxqalctjyegbvouezfiqoeoazizhmjhpbmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"8 3\\naeabcbey\\n\", \"40 13\\nwlpchuqrxdmkgdhayykfvaccysprpsosdpgszjwv\\n\", \"198 36\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"198 11\\ntuvldeatellucfucuyjxqvapqvinjipxepsncuvmnrqvpsqqlfnqvpqvwhtmeowiqfvrvfrzfzfyqschlibgljtwpetfswzbnowdpymjymrsqfyfsvnpgtfwjpsabsxjxttfwxmdtgfrrdsoczvmcwpuekxgrykjvyvmcphjmhzizaoeoqifzeuovbgeyjtclaqxut\\n\", \"93 61\\nuecrsqsoylbotwcujcsbjohlyjlpjsjsnvttpytrvztqtkpsdcrvsossimwmglulwzpouhaiqvowthzsyonwjjearhniq\\n\", \"57 11\\nibkypcbtpdlhhpmghwrmuwaqoqxxexxqoqawumrwhgmphhldixezufpqh\\n\", \"46 33\\nxxzkzsxlyhotmfjoptrilatgvqpyshraiycmyzzlrclltu\\n\", \"40 13\\nwlpchuqrxdmjgdhayykfvaccysprpsosdpgszjwv\\n\", \"57 11\\nibkypcbtpdlhhpmghwrmuwaqoqxxexxqoqawumrwhgmphhldixezufqqh\\n\", \"198 36\\ntuvldeatellucfucuyjxqvapqvinjipxepsncuvmnrqvpsqqlfnqvpqvwhtmeowiqfvrvfrzfzfyqschlibgljtwpetfswzbnowdpymkymrsqfyfsvnpgtfwjpsabsxjxttfwxmdtgfrrdsoczvmcwpuekxgrykjvyvmcphjmhzizaoeoqifzeuovbgeyjtclaqxut\\n\", \"5 5\\npjfjc\\n\", \"10 3\\nabcddddcef\\n\", \"167 152\\nvqgjxbuxevpqbpnuyxktgpwdgyebnmrxbnitphshuloyykpgxakxadtguqskmhejndzpcproeabnlvfwdyjiydfrjkxpvpbzwutsdpfawwcqqqirxwlkrettlnpdeccaoqetcaqcvyjtfoekyupvbsoiyldggycphddecbf\\n\", \"85 19\\nblkimwzicvbdkwgodvukdofndwtwllhnqffroidvxbeesatbguvjkbouwtonjunmvgivdofwkdbvcizwmiklb\\n\", \"46 29\\nxxzkzsxlyhotmfjpptrilatgvqpyshraiycmyzzlrclltu\\n\", \"198 48\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"8 8\\naccedbba\\n\", \"8 3\\nzebcbaea\\n\", \"5 1\\npjgjb\\n\", \"4 4\\nkoar\\n\", \"46 32\\nxxzkzsxlyhotmfjpptrilatgvqpyshraiycmyzzlrclltu\\n\", \"40 23\\nwlpchuqrxdmkgdhayykfvaccysprpsosdpgszjwv\\n\", \"4 4\\noark\\n\", \"198 8\\ntuvldeatellucfucuyjxqvapqvinjipxepsncuvmnrqvpsqqlfnqvpqvwhtmeowiqfvrvfrzfzfyqschlibgljtwpetfswzbnowdpymjymrsqfyfsvnpgtfwjpsabsxjxttfwxmdtgfrrdsoczvmcwpuekxgrykjvyvmcphjmhzizaoeoqifzeuovbgeyjtclaqxut\\n\", \"5 5\\nbjfjp\\n\", \"4 4\\nkroa\\n\", \"8 8\\naccedcaa\\n\", \"8 3\\nadabcaez\\n\", \"2 2\\nua\\n\", \"198 4\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwvftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlsut\\n\", \"5 1\\nbjgjp\\n\", \"46 33\\nxxzkzsxlyhotmfjpptrilatgvqpyshraiycmyzzlrclltu\\n\", \"4 4\\naork\\n\", \"5 5\\nbkfjp\\n\", \"8 8\\naccedcab\\n\", \"198 36\\ntuvldeatellucfucuyjxqvapqvinjipxepsncuvmnrqvpsqqlfnqvpqvwhtmeowiqfvrvfrzfzfyqschlibgljtwpetfswzbnowdpymjymrsqfyfsvnpgtfwjpsabsxjxttfwxmdtgfrrdsoczvmcwpuekxgrykjvyvmcphjmhzizaoeoqifzeuovbgeyjtclaqxut\\n\", \"93 61\\nqinhraejjwnoyszhtwovqiahuopzwlulgmwmissosvrcdspktqtzvrtypttvnsjsjpljylhojbscjucwtoblyosqsrceu\\n\", \"8 1\\naccedcab\\n\", \"40 13\\nvwjzsgpdsosprpsyccavfkyyahdgjmdxrquhcplw\\n\", \"93 61\\nqinhraejjwnoyszhtwovqiahuopzwlulgmwmissosvrcdspktqtzvrtypttvnsjsjqljylhojbscjucwtoblyosqsrceu\\n\", \"57 11\\nhqqfuzexidlhhpmghwrmuwaqoqxxexxqoqawumrwhgmphhldptbcpykbi\\n\", \"10 8\\nabcdeedcba\\n\", \"2 2\\nas\\n\", \"46 29\\nyxzkzsxlyhotmfjpptrilatgtqpyshraiycmyzzlrcllvu\\n\", \"8 8\\nacceccba\\n\", \"198 3\\ntuxqalctjyegbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwftsxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexpijnivqpavqxjyucufculletaedlvut\\n\", \"8 3\\nzebebaca\\n\", \"167 40\\nvqgjxbuxevpqbpnuyxktgpwdgyebnmrxbnitphshuloyykpgxakxadtguqskmhejndzptproeabnlvfwdyjiydfrjkxpvpbzwutsdpfawwcqqqirxwlkrectlnpdeccaoqetcaqcvyjtfoekyupvbsoiyldggycphddecbf\\n\", \"198 6\\ntuxqalctjypgbvouezfiqoeoazizhmjhpcmvyvjkyrgxkeupwcmvzcosdrrfgtdmxwfttxjxsbaspjwftgpnvsfyfqsrmyjmypdwonbzwsftepwtjlgbilhcsqyfzfzrfvrvfqiwoemthwvqpvqnflqqspvqrnmvucnspexeijnivqpavqxjyucufculletaedlvut\\n\", \"167 44\\nvqgjxbuxevpqbpnuyxktgpwdgyebnmrxbnitphshuloyykpgxakxadtguqskmhejndzptproeabnlvfwdyjiydfrjkxpvpbzwutsdpfawwcqqqirxwlkrectlnpdeccaoqetcaqcvyjtfoekyupvbsoiyldggycphddecbf\\n\", \"4 4\\nkrob\\n\", \"8 3\\naeabcaez\\n\"], \"outputs\": [\"6\\n\", \"3\\n\", \"14\\n\", \"138\\n\", \"169\\n\", \"0\\n\", \"12\\n\", \"55\\n\", \"1\\n\", \"666\\n\", \"367\\n\", \"0\\n\", \"187\\n\", \"692\\n\", \"168\\n\", \"0\\n\", \"7\\n\", \"11\\n\", \"5\\n\", \"0\\n\", \"12\\n\", \"0\\n\", \"0\\n\", \"7\\n\", \"14\\n\", \"11\\n\", \"168\\n\", \"692\\n\", \"1\\n\", \"3\\n\", \"187\\n\", \"666\\n\", \"0\\n\", \"367\\n\", \"0\\n\", \"5\\n\", \"55\\n\", \"169\\n\", \"138\\n\", \"6\\n\", \"688\\n\", \"675\\n\", \"5\\n\", \"7\\n\", \"689\\n\", \"687\\n\", \"12\\n\", \"20\\n\", \"171\\n\", \"187\\n\", \"666\\n\", \"362\\n\", \"169\\n\", \"691\\n\", \"672\\n\", \"695\\n\", \"14\\n\", \"699\\n\", \"711\\n\", \"693\\n\", \"0\\n\", \"11\\n\", \"366\\n\", \"54\\n\", \"172\\n\", \"653\\n\", \"690\\n\", \"8\\n\", \"174\\n\", \"721\\n\", \"696\\n\", \"367\\n\", \"56\\n\", \"173\\n\", \"175\\n\", \"57\\n\", \"722\\n\", \"13\\n\", \"10\\n\", \"674\\n\", \"196\\n\", \"168\\n\", \"733\\n\", \"6\\n\", \"7\\n\", \"12\\n\", \"20\\n\", \"171\\n\", \"169\\n\", \"14\\n\", \"693\\n\", \"12\\n\", \"14\\n\", \"6\\n\", \"7\\n\", \"6\\n\", \"695\\n\", \"12\\n\", \"172\\n\", \"14\\n\", \"14\\n\", \"7\\n\", \"721\\n\", \"367\\n\", \"7\\n\", \"175\\n\", \"366\\n\", \"57\\n\", \"0\\n\", \"8\\n\", \"169\\n\", \"6\\n\", \"689\\n\", \"11\\n\", \"690\\n\", \"687\\n\", \"690\\n\", \"13\\n\", \"6\\n\"]}", "source": "taco"}
|
Nam is playing with a string on his computer. The string consists of n lowercase English letters. It is meaningless, so Nam decided to make the string more beautiful, that is to make it be a palindrome by using 4 arrow keys: left, right, up, down.
There is a cursor pointing at some symbol of the string. Suppose that cursor is at position i (1 ≤ i ≤ n, the string uses 1-based indexing) now. Left and right arrow keys are used to move cursor around the string. The string is cyclic, that means that when Nam presses left arrow key, the cursor will move to position i - 1 if i > 1 or to the end of the string (i. e. position n) otherwise. The same holds when he presses the right arrow key (if i = n, the cursor appears at the beginning of the string).
When Nam presses up arrow key, the letter which the text cursor is pointing to will change to the next letter in English alphabet (assuming that alphabet is also cyclic, i. e. after 'z' follows 'a'). The same holds when he presses the down arrow key.
Initially, the text cursor is at position p.
Because Nam has a lot homework to do, he wants to complete this as fast as possible. Can you help him by calculating the minimum number of arrow keys presses to make the string to be a palindrome?
-----Input-----
The first line contains two space-separated integers n (1 ≤ n ≤ 10^5) and p (1 ≤ p ≤ n), the length of Nam's string and the initial position of the text cursor.
The next line contains n lowercase characters of Nam's string.
-----Output-----
Print the minimum number of presses needed to change string into a palindrome.
-----Examples-----
Input
8 3
aeabcaez
Output
6
-----Note-----
A string is a palindrome if it reads the same forward or reversed.
In the sample test, initial Nam's string is: $\text{aeabcaez}$ (cursor position is shown bold).
In optimal solution, Nam may do 6 following steps:[Image]
The result, $\text{zeaccaez}$, is now a palindrome.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\\n3 1 2\", \"3\\n1 2 3\", \"4\\n2 3 1 4\", \"4\\n1 3 4 2\", \"8\\n5 3 8 1 2 6 7 4\", \"4\\n3 2 4 1\", \"8\\n4 5 8 1 2 6 7 3\", \"3\\n1 3 2\", \"3\\n2 3 1\", \"3\\n3 2 1\", \"4\\n2 3 4 1\", \"4\\n1 2 3 4\", \"3\\n3 1 2\", \"3\\n3 2 1\", \"3\\n1 2 3\", \"3\\n1 3 2\", \"3\\n2 3 1\", \"4\\n1 4 3 2\", \"4\\n2 3 1 4\", \"4\\n1 4 2 3\", \"3\\n2 1 3\", \"4\\n1 3 2 4\", \"8\\n5 4 8 1 2 6 7 3\"], \"outputs\": [\"9\\n\", \"10\\n\", \"17\\n\", \"20\\n\", \"84\\n\", \"19\\n\", \"86\\n\", \"10\\n\", \"10\\n\", \"10\\n\", \"20\\n\", \"20\\n\", \"9\\n\", \"10\\n\", \"10\\n\", \"10\\n\", \"10\\n\", \"20\\n\", \"17\\n\", \"19\\n\", \"9\", \"19\", \"85\"]}", "source": "taco"}
|
One day, Snuke was given a permutation of length N, a_1, a_2, ..., a_N, from his friend.
Find the following:
<image>
Constraints
* 1 ≦ N ≦ 200,000
* (a_1, a_2, ..., a_N) is a permutation of (1, 2, ..., N).
Input
The input is given from Standard Input in the following format:
N
a_1 a_2 ... a_N
Output
Print the answer.
Note that the answer may not fit into a 32-bit integer.
Examples
Input
3
2 1 3
Output
9
Input
4
1 3 2 4
Output
19
Input
8
5 4 8 1 2 6 7 3
Output
85
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"5\\n1 2 2 4 3\\n\", \"3\\n4 1 1\\n\", \"4\\n0 3 0 4\\n\", \"5\\n4 4 3 3 1\\n\", \"5\\n4 3 4 2 4\\n\", \"10\\n2 1 2 3 4 1 3 4 4 4\\n\", \"10\\n2 3 3 1 3 1 3 2 2 4\\n\", \"120\\n1 1 1 1 1 1 1 4 4 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 4 1 1 4 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 1 1 1 2 4 1 1 3 1 1 1 2 1 0 3 1 1 1 2 1 4 1 1 1 1 1 1 1 1 1 1\\n\", \"10\\n2 4 1 3 1 2 2 2 2 2\\n\", \"10\\n3 4 2 2 1 1 3 1 1 2\\n\", \"20\\n4 1 4 4 2 1 4 3 2 3 1 1 2 2 2 4 4 2 4 2\\n\", \"20\\n4 3 4 2 1 1 3 1 4 2 1 4 3 3 4 3 1 1 1 3\\n\", \"20\\n4 1 1 1 4 2 3 3 2 1 1 4 4 3 1 1 2 4 2 3\\n\", \"20\\n4 4 2 4 3 2 3 1 4 1 1 4 1 4 3 4 4 3 3 3\\n\", \"20\\n4 2 3 3 1 3 2 3 1 4 4 4 2 1 4 2 1 3 4 4\\n\", \"23\\n2 3 1 1 1 1 4 3 2 2 3 3 4 1 4 2 4 1 4 2 3 1 1\\n\", \"27\\n0 2 4 1 4 2 1 2 3 4 2 4 1 2 3 2 3 2 2 1 0 4 3 0 3 0 1\\n\", \"28\\n2 0 4 2 3 4 1 1 4 3 0 3 0 3 2 3 2 4 1 2 4 3 3 3 0 1 0 1\\n\", \"24\\n4 2 4 3 1 3 4 1 3 4 2 4 0 2 3 4 1 1 4 3 1 2 2 4\\n\", \"19\\n2 4 4 2 0 0 1 4 1 0 2 2 4 2 0 1 1 1 4\\n\", \"16\\n3 3 3 1 3 0 1 4 4 4 1 4 3 1 1 4\\n\", \"17\\n3 3 1 0 1 3 1 1 1 3 0 2 2 2 3 2 2\\n\", \"12\\n2 2 2 1 1 0 2 0 1 1 2 1\\n\", \"15\\n4 0 1 0 0 4 1 1 0 4 1 4 4 1 0\\n\", \"20\\n0 4 4 0 0 0 2 3 3 3 2 0 3 2 3 2 4 4 2 4\\n\", \"23\\n1 1 3 2 0 3 1 2 2 2 1 3 3 4 1 0 0 3 1 2 2 0 3\\n\", \"15\\n0 2 4 2 0 4 4 2 4 4 1 2 4 2 2\\n\", \"17\\n0 4 3 0 2 2 4 2 4 4 2 4 2 1 0 0 0\\n\", \"21\\n0 3 2 3 0 2 3 4 3 0 1 3 2 2 3 3 3 0 2 2 0\\n\", \"21\\n1 1 3 1 0 3 3 3 3 0 1 3 0 3 1 1 1 3 2 0 0\\n\", \"13\\n1 1 1 2 1 1 4 1 3 1 1 1 0\\n\", \"14\\n4 2 4 4 0 4 4 0 1 0 0 4 3 4\\n\", \"13\\n2 1 2 2 3 4 0 2 2 2 2 2 2\\n\", \"10\\n2 2 2 0 0 0 0 0 2 2\\n\", \"11\\n2 2 2 2 0 2 2 2 2 2 2\\n\", \"11\\n1 1 1 1 1 1 1 1 1 1 1\\n\", \"16\\n0 0 1 1 1 1 1 1 1 1 1 0 1 1 0 1\\n\", \"17\\n1 1 4 1 1 0 1 1 1 1 0 1 0 1 0 0 1\\n\", \"14\\n1 0 0 1 1 1 0 1 1 1 1 1 3 0\\n\", \"9\\n1 1 1 2 1 1 1 1 1\\n\", \"13\\n2 2 0 4 2 2 2 2 2 1 2 2 2\\n\", \"19\\n2 2 3 2 0 0 1 1 2 0 0 2 1 2 2 2 0 2 2\\n\", \"29\\n3 1 3 3 0 2 2 3 3 2 0 3 3 2 3 0 3 3 0 2 2 2 3 2 0 3 2 2 3\\n\", \"27\\n0 1 2 2 3 3 2 0 2 3 2 0 2 3 2 2 2 2 3 3 1 3 2 3 1 2 2\\n\", \"29\\n3 3 2 0 1 1 1 2 2 2 1 3 2 0 2 3 3 2 2 3 2 2 2 2 1 2 2 2 4\\n\", \"13\\n4 1 1 4 1 1 1 1 1 1 1 1 1\\n\", \"30\\n1 1 1 3 3 4 0 1 1 1 1 1 1 3 0 0 0 1 1 1 1 3 1 1 1 1 3 1 1 1\\n\", \"32\\n1 4 4 3 1 4 4 4 1 1 1 1 1 4 1 1 1 4 1 1 1 1 2 1 1 4 4 1 1 1 1 4\\n\", \"48\\n1 3 1 1 1 1 1 1 2 1 1 2 1 1 4 1 1 1 2 2 2 1 3 1 1 1 1 2 1 2 2 1 1 1 1 1 3 0 2 3 1 1 3 1 0 1 2 1\\n\", \"49\\n2 2 1 2 2 2 2 2 2 2 2 2 1 2 1 3 4 2 2 2 2 4 1 1 2 1 2 2 2 2 2 4 0 0 2 0 1 1 2 1 2 2 2 2 4 4 2 2 1\\n\", \"165\\n1 1 1 1 1 1 1 1 0 2 2 2 1 1 1 1 1 4 4 1 1 2 2 1 2 1 2 2 2 1 2 2 3 1 1 2 1 1 2 2 4 1 2 2 2 4 1 1 1 4 2 2 1 1 1 1 1 2 1 1 1 2 1 1 1 1 4 2 2 1 1 1 1 2 1 1 1 1 2 2 1 1 2 1 1 1 1 2 2 1 2 1 2 1 2 2 1 2 2 1 1 1 2 1 4 2 2 2 1 1 1 1 2 3 2 1 2 1 1 2 1 1 1 1 1 2 1 2 1 1 0 1 2 1 1 1 1 1 3 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 2 3 4 1 1 1\\n\", \"197\\n1 4 4 4 1 4 1 1 0 1 4 4 1 1 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 4 1 1 1 1 1 4 1 1 1 2 1 1 4 4 4 4 4 4 1 1 1 4 1 4 4 4 4 4 1 1 1 1 1 4 4 1 4 0 4 1 4 4 1 4 4 4 2 1 1 4 4 2 1 1 1 4 1 4 1 4 4 4 1 1 4 4 4 1 1 0 1 4 1 4 0 4 3 1 1 1 4 1 4 4 4 1 4 1 4 3 1 4 4 4 1 1 4 0 4 1 1 4 1 4 4 1 4 1 1 1 4 1 4 1 1 3 4 1 4 4 1 1 1 1 4 1 1 3 4 1 1 0 1 4 4 1 4 4 1 4 4 1 1 0 2 1 4 1 4 1 1 1 1 1 4 4 1 1 0 4 2 4 1 4 1 4 4\\n\", \"177\\n2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 4 2 2 2 2 4 2 0 2 2 2 2 2 3 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 4 2 2 2 2 2 2 4 2 2 2 2 2 3 2 1 2 2 2 2 2 2 4 4 2 2 2 4 2 2 2 2 2 2 2 2 4 2 4 2 2 4 2 2 2 2 2 2 2 2 0 2 3 2 2 2 2 2 2 2 0 2 2 4 2 2 2 2 3 2 2\\n\", \"166\\n2 3 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 3 2 2 2 2 2 2 2 2 2 4 2 2 2 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 2 2 2 2 2 2 2 2 2 3 2 0 2 0 3 2 2 2 0 2 0 2 2 2 2 2 2 3 0 2 2 2 2 2 3 3 2 2 2 3 2 2 2 3 3 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 3 2 2 2 2\\n\", \"172\\n2 2 2 0 1 3 2 1 0 3 3 1 0 1 2 3 4 2 2 4 2 1 4 0 3 2 2 3 3 3 0 0 3 1 1 0 1 2 2 0 1 4 4 0 3 3 2 0 1 4 4 1 4 2 2 3 0 1 2 2 1 1 4 4 4 4 0 1 0 2 4 0 2 0 0 2 2 1 4 2 2 2 2 2 0 2 3 0 2 1 0 2 1 0 2 2 0 2 2 0 2 2 2 1 1 0 2 1 2 1 0 2 2 0 2 2 3 2 4 2 4 3 2 3 1 2 2 4 0 2 0 2 2 1 0 1 2 1 4 1 0 3 2 2 1 0 0 2 0 4 2 2 0 0 4 1 3 2 1 1 0 2 3 2 0 2 2 2 2 2 3 0\\n\", \"141\\n2 1 1 1 1 1 4 2 3 1 1 1 1 1 1 4 1 1 1 1 1 1 1 4 4 1 1 1 1 2 1 4 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 2 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 3 1 1 1 1 1 4 4 1 3 4 1 1 1 1 1 1 1 1 1 4 2 1 0 1 1 4 1 1 1 1 2 1 0 1 1 2 1 1 1 1 4 4 1 2 4 4 1 1 3 1 1 1 3 1 1 4 4 1 1 1 4 1 1 1 1 1 1 2 0 1 0 0 1 0 4\\n\", \"108\\n2 2 1 4 2 2 1 2 2 2 2 2 2 4 2 2 4 2 4 2 2 2 2 4 2 4 2 2 2 1 2 1 2 2 2 4 2 2 2 2 2 2 4 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 4 2 1 2 2 2 2 2 2 2 2 2 2 1 2 2 4 2 2 2 2 4 2 2 2 1 2 2 2 2 2 4 1 2 2\\n\", \"138\\n3 1 3 1 3 3 3 1 1 1 1 1 1 3 3 1 1 1 3 3 1 1 3 1 1 1 1 1 1 1 3 3 3 1 3 1 1 1 1 1 3 1 1 3 1 3 1 3 1 1 1 1 3 1 3 1 1 3 1 1 1 3 1 1 1 1 1 1 1 1 3 1 1 1 1 3 1 3 1 3 3 3 3 3 3 1 1 1 3 1 1 3 1 1 1 1 1 1 1 1 3 1 1 3 3 1 3 3 1 3 1 1 1 3 1 1 1 1 1 1 3 1 1 1 1 3 1 1 1 3 1 1 3 1 1 3 1 1\\n\", \"81\\n2 2 2 3 2 3 2 2 2 2 2 3 2 2 2 2 2 2 0 2 4 2 3 4 2 3 2 3 2 0 2 2 0 2 2 3 2 2 4 3 3 2 2 2 2 2 2 2 3 2 2 2 2 2 2 3 3 2 2 3 2 0 2 0 2 2 2 2 2 2 4 0 2 3 2 4 2 2 2 2 2\\n\", \"115\\n2 2 2 2 4 2 2 2 2 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 4 2 4 2 4 2 2 2 2 2 2 2 2 2 2 2 4 4 3 2 2 2 2 2 2 2 4 2 2 2 3 2 2 2 2 2 2 4 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 3 2 2 2 2 2 4 4 4 2 2\\n\", \"146\\n1 1 1 1 1 4 1 1 0 1 4 4 1 4 1 1 1 1 1 4 1 1 1 1 1 1 1 4 1 1 1 1 4 1 4 1 1 1 0 1 4 1 4 1 4 4 1 1 1 1 1 1 1 1 1 4 4 1 1 4 1 4 4 4 1 1 4 4 1 4 1 1 1 1 0 1 1 1 1 1 1 4 1 4 1 1 4 1 1 4 4 4 1 1 4 1 1 1 1 1 1 1 4 1 1 1 4 1 4 1 1 1 1 1 1 1 4 1 1 4 4 4 1 1 1 1 1 1 1 4 1 1 1 1 4 1 4 1 1 1 4 4 4 4 1 1\\n\", \"198\\n1 2 1 2 2 1 2 1 1 1 3 2 1 1 2 1 2 2 1 1 1 4 1 1 1 1 0 1 1 1 1 4 1 1 3 1 2 1 1 1 2 1 2 0 1 1 1 1 1 1 1 1 1 2 4 4 1 0 1 1 1 1 1 1 1 1 2 1 1 1 4 0 1 2 1 2 1 1 2 2 1 1 1 1 3 2 2 2 1 1 4 1 2 2 2 1 1 2 2 1 2 2 2 1 1 1 1 3 1 3 1 1 0 1 4 1 2 2 1 1 1 2 2 1 1 1 1 3 2 1 2 1 1 2 1 2 1 2 1 0 4 1 2 1 1 1 1 3 1 1 2 0 1 1 1 1 1 3 2 1 2 1 1 0 1 1 3 1 1 2 1 1 1 1 1 1 4 4 1 1 0 1 1 1 2 1 1 1 3 0 2 1 2 1 1 1 1 1\\n\", \"200\\n4 1 1 4 3 1 1 3 1 1 1 4 3 3 3 2 3 3 1 3 3 4 4 2 2 2 3 1 2 2 2 3 1 1 3 2 2 4 1 3 4 3 2 4 2 2 4 2 2 3 4 2 3 2 2 1 2 4 4 2 4 4 2 3 2 4 1 4 2 1 3 4 1 3 1 1 2 1 4 1 3 3 3 4 1 4 4 1 4 4 2 3 1 3 3 2 2 1 4 2 4 4 3 3 3 1 3 4 3 1 1 1 1 4 2 1 2 3 2 2 2 3 2 1 2 1 1 1 2 4 1 3 3 3 2 3 3 2 3 4 4 3 3 4 3 2 1 4 1 4 2 1 3 2 4 4 1 4 1 1 1 3 2 3 4 2 2 4 1 4 4 4 4 3 1 3 1 4 3 2 1 2 1 1 2 4 1 3 3 4 4 2 2 4 4 3 2 1 2 4\\n\", \"200\\n2 1 1 2 2 2 2 1 1 2 2 2 1 1 2 2 2 2 1 1 1 2 2 2 2 2 2 1 2 2 1 1 1 1 2 1 2 2 1 2 2 2 2 1 2 2 1 1 1 1 2 2 1 1 1 1 1 2 2 2 2 1 2 1 2 2 2 2 1 1 1 2 1 2 2 2 2 1 1 1 1 1 1 2 2 2 1 2 2 2 1 2 2 2 1 1 1 2 2 1 1 1 1 2 2 1 2 1 1 1 2 2 1 1 2 2 2 1 2 2 0 1 2 1 1 2 2 2 1 2 2 1 1 1 2 2 2 1 2 1 2 1 2 1 1 2 2 1 1 1 1 1 2 2 1 1 1 1 1 2 1 2 2 1 1 1 1 1 1 2 2 1 1 1 1 2 2 1 1 1 2 2 2 2 1 1 1 1 1 1 2 1 1 2 2 1 1 2 1 0\\n\", \"6\\n1 1 1 2 2 1\\n\", \"10\\n3 3 1 1 2 1 1 1 2 2\\n\", \"10\\n1 1 1 2 1 2 2 1 2 1\\n\", \"15\\n1 2 2 1 2 3 2 1 2 1 1 1 2 1 1\\n\", \"13\\n2 1 2 2 1 0 1 2 1 1 1 1 2\\n\", \"3\\n4 4 1\\n\", \"5\\n4 4 4 4 1\\n\", \"1\\n1\\n\", \"4\\n1 1 3 4\\n\", \"7\\n1 1 1 3 3 3 3\\n\", \"6\\n2 2 2 4 4 4\\n\", \"3\\n2 3 3\\n\", \"9\\n1 1 1 1 3 3 3 3 3\\n\", \"3\\n1 4 4\\n\", \"3\\n3 3 2\\n\", \"5\\n1 1 1 1 1\\n\", \"2\\n1 1\\n\", \"3\\n1 1 3\\n\", \"4\\n2 2 2 2\\n\", \"6\\n2 2 2 2 2 4\\n\", \"3\\n2 2 4\\n\", \"2\\n2 3\\n\", \"2\\n1 4\\n\", \"4\\n1 1 3 3\\n\", \"4\\n3 3 3 2\\n\", \"1\\n4\\n\", \"20\\n4 2 3 3 1 3 2 3 1 4 4 4 2 1 4 2 1 3 4 4\\n\", \"166\\n2 3 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 3 2 2 2 2 2 2 2 2 2 4 2 2 2 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 2 2 2 2 2 2 2 2 2 3 2 0 2 0 3 2 2 2 0 2 0 2 2 2 2 2 2 3 0 2 2 2 2 2 3 3 2 2 2 3 2 2 2 3 3 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 3 2 2 2 2\\n\", \"20\\n4 3 4 2 1 1 3 1 4 2 1 4 3 3 4 3 1 1 1 3\\n\", \"3\\n1 1 3\\n\", \"3\\n2 3 3\\n\", \"4\\n1 1 3 4\\n\", \"2\\n1 1\\n\", \"14\\n1 0 0 1 1 1 0 1 1 1 1 1 3 0\\n\", \"19\\n2 2 3 2 0 0 1 1 2 0 0 2 1 2 2 2 0 2 2\\n\", \"5\\n1 1 1 1 1\\n\", \"23\\n1 1 3 2 0 3 1 2 2 2 1 3 3 4 1 0 0 3 1 2 2 0 3\\n\", \"13\\n4 1 1 4 1 1 1 1 1 1 1 1 1\\n\", \"108\\n2 2 1 4 2 2 1 2 2 2 2 2 2 4 2 2 4 2 4 2 2 2 2 4 2 4 2 2 2 1 2 1 2 2 2 4 2 2 2 2 2 2 4 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 4 2 1 2 2 2 2 2 2 2 2 2 2 1 2 2 4 2 2 2 2 4 2 2 2 1 2 2 2 2 2 4 1 2 2\\n\", \"165\\n1 1 1 1 1 1 1 1 0 2 2 2 1 1 1 1 1 4 4 1 1 2 2 1 2 1 2 2 2 1 2 2 3 1 1 2 1 1 2 2 4 1 2 2 2 4 1 1 1 4 2 2 1 1 1 1 1 2 1 1 1 2 1 1 1 1 4 2 2 1 1 1 1 2 1 1 1 1 2 2 1 1 2 1 1 1 1 2 2 1 2 1 2 1 2 2 1 2 2 1 1 1 2 1 4 2 2 2 1 1 1 1 2 3 2 1 2 1 1 2 1 1 1 1 1 2 1 2 1 1 0 1 2 1 1 1 1 1 3 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 2 3 4 1 1 1\\n\", \"4\\n1 1 3 3\\n\", \"12\\n2 2 2 1 1 0 2 0 1 1 2 1\\n\", \"48\\n1 3 1 1 1 1 1 1 2 1 1 2 1 1 4 1 1 1 2 2 2 1 3 1 1 1 1 2 1 2 2 1 1 1 1 1 3 0 2 3 1 1 3 1 0 1 2 1\\n\", \"5\\n4 4 4 4 1\\n\", \"197\\n1 4 4 4 1 4 1 1 0 1 4 4 1 1 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 4 1 1 1 1 1 4 1 1 1 2 1 1 4 4 4 4 4 4 1 1 1 4 1 4 4 4 4 4 1 1 1 1 1 4 4 1 4 0 4 1 4 4 1 4 4 4 2 1 1 4 4 2 1 1 1 4 1 4 1 4 4 4 1 1 4 4 4 1 1 0 1 4 1 4 0 4 3 1 1 1 4 1 4 4 4 1 4 1 4 3 1 4 4 4 1 1 4 0 4 1 1 4 1 4 4 1 4 1 1 1 4 1 4 1 1 3 4 1 4 4 1 1 1 1 4 1 1 3 4 1 1 0 1 4 4 1 4 4 1 4 4 1 1 0 2 1 4 1 4 1 1 1 1 1 4 4 1 1 0 4 2 4 1 4 1 4 4\\n\", \"10\\n3 3 1 1 2 1 1 1 2 2\\n\", \"198\\n1 2 1 2 2 1 2 1 1 1 3 2 1 1 2 1 2 2 1 1 1 4 1 1 1 1 0 1 1 1 1 4 1 1 3 1 2 1 1 1 2 1 2 0 1 1 1 1 1 1 1 1 1 2 4 4 1 0 1 1 1 1 1 1 1 1 2 1 1 1 4 0 1 2 1 2 1 1 2 2 1 1 1 1 3 2 2 2 1 1 4 1 2 2 2 1 1 2 2 1 2 2 2 1 1 1 1 3 1 3 1 1 0 1 4 1 2 2 1 1 1 2 2 1 1 1 1 3 2 1 2 1 1 2 1 2 1 2 1 0 4 1 2 1 1 1 1 3 1 1 2 0 1 1 1 1 1 3 2 1 2 1 1 0 1 1 3 1 1 2 1 1 1 1 1 1 4 4 1 1 0 1 1 1 2 1 1 1 3 0 2 1 2 1 1 1 1 1\\n\", \"6\\n2 2 2 2 2 4\\n\", \"3\\n4 4 1\\n\", \"29\\n3 1 3 3 0 2 2 3 3 2 0 3 3 2 3 0 3 3 0 2 2 2 3 2 0 3 2 2 3\\n\", \"23\\n2 3 1 1 1 1 4 3 2 2 3 3 4 1 4 2 4 1 4 2 3 1 1\\n\", \"81\\n2 2 2 3 2 3 2 2 2 2 2 3 2 2 2 2 2 2 0 2 4 2 3 4 2 3 2 3 2 0 2 2 0 2 2 3 2 2 4 3 3 2 2 2 2 2 2 2 3 2 2 2 2 2 2 3 3 2 2 3 2 0 2 0 2 2 2 2 2 2 4 0 2 3 2 4 2 2 2 2 2\\n\", \"10\\n2 4 1 3 1 2 2 2 2 2\\n\", \"9\\n1 1 1 1 3 3 3 3 3\\n\", \"21\\n1 1 3 1 0 3 3 3 3 0 1 3 0 3 1 1 1 3 2 0 0\\n\", \"19\\n2 4 4 2 0 0 1 4 1 0 2 2 4 2 0 1 1 1 4\\n\", \"28\\n2 0 4 2 3 4 1 1 4 3 0 3 0 3 2 3 2 4 1 2 4 3 3 3 0 1 0 1\\n\", \"17\\n3 3 1 0 1 3 1 1 1 3 0 2 2 2 3 2 2\\n\", \"10\\n2 1 2 3 4 1 3 4 4 4\\n\", \"200\\n2 1 1 2 2 2 2 1 1 2 2 2 1 1 2 2 2 2 1 1 1 2 2 2 2 2 2 1 2 2 1 1 1 1 2 1 2 2 1 2 2 2 2 1 2 2 1 1 1 1 2 2 1 1 1 1 1 2 2 2 2 1 2 1 2 2 2 2 1 1 1 2 1 2 2 2 2 1 1 1 1 1 1 2 2 2 1 2 2 2 1 2 2 2 1 1 1 2 2 1 1 1 1 2 2 1 2 1 1 1 2 2 1 1 2 2 2 1 2 2 0 1 2 1 1 2 2 2 1 2 2 1 1 1 2 2 2 1 2 1 2 1 2 1 1 2 2 1 1 1 1 1 2 2 1 1 1 1 1 2 1 2 2 1 1 1 1 1 1 2 2 1 1 1 1 2 2 1 1 1 2 2 2 2 1 1 1 1 1 1 2 1 1 2 2 1 1 2 1 0\\n\", \"177\\n2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 4 2 2 2 2 4 2 0 2 2 2 2 2 3 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 4 2 2 2 2 2 2 4 2 2 2 2 2 3 2 1 2 2 2 2 2 2 4 4 2 2 2 4 2 2 2 2 2 2 2 2 4 2 4 2 2 4 2 2 2 2 2 2 2 2 0 2 3 2 2 2 2 2 2 2 0 2 2 4 2 2 2 2 3 2 2\\n\", \"16\\n0 0 1 1 1 1 1 1 1 1 1 0 1 1 0 1\\n\", \"1\\n1\\n\", \"141\\n2 1 1 1 1 1 4 2 3 1 1 1 1 1 1 4 1 1 1 1 1 1 1 4 4 1 1 1 1 2 1 4 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 2 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 3 1 1 1 1 1 4 4 1 3 4 1 1 1 1 1 1 1 1 1 4 2 1 0 1 1 4 1 1 1 1 2 1 0 1 1 2 1 1 1 1 4 4 1 2 4 4 1 1 3 1 1 1 3 1 1 4 4 1 1 1 4 1 1 1 1 1 1 2 0 1 0 0 1 0 4\\n\", \"49\\n2 2 1 2 2 2 2 2 2 2 2 2 1 2 1 3 4 2 2 2 2 4 1 1 2 1 2 2 2 2 2 4 0 0 2 0 1 1 2 1 2 2 2 2 4 4 2 2 1\\n\", \"17\\n1 1 4 1 1 0 1 1 1 1 0 1 0 1 0 0 1\\n\", \"27\\n0 1 2 2 3 3 2 0 2 3 2 0 2 3 2 2 2 2 3 3 1 3 2 3 1 2 2\\n\", \"15\\n4 0 1 0 0 4 1 1 0 4 1 4 4 1 0\\n\", \"138\\n3 1 3 1 3 3 3 1 1 1 1 1 1 3 3 1 1 1 3 3 1 1 3 1 1 1 1 1 1 1 3 3 3 1 3 1 1 1 1 1 3 1 1 3 1 3 1 3 1 1 1 1 3 1 3 1 1 3 1 1 1 3 1 1 1 1 1 1 1 1 3 1 1 1 1 3 1 3 1 3 3 3 3 3 3 1 1 1 3 1 1 3 1 1 1 1 1 1 1 1 3 1 1 3 3 1 3 3 1 3 1 1 1 3 1 1 1 1 1 1 3 1 1 1 1 3 1 1 1 3 1 1 3 1 1 3 1 1\\n\", \"3\\n2 2 4\\n\", \"24\\n4 2 4 3 1 3 4 1 3 4 2 4 0 2 3 4 1 1 4 3 1 2 2 4\\n\", \"6\\n1 1 1 2 2 1\\n\", \"7\\n1 1 1 3 3 3 3\\n\", \"29\\n3 3 2 0 1 1 1 2 2 2 1 3 2 0 2 3 3 2 2 3 2 2 2 2 1 2 2 2 4\\n\", \"1\\n4\\n\", \"2\\n1 4\\n\", \"13\\n2 1 2 2 3 4 0 2 2 2 2 2 2\\n\", \"17\\n0 4 3 0 2 2 4 2 4 4 2 4 2 1 0 0 0\\n\", \"15\\n0 2 4 2 0 4 4 2 4 4 1 2 4 2 2\\n\", \"5\\n4 3 4 2 4\\n\", \"20\\n0 4 4 0 0 0 2 3 3 3 2 0 3 2 3 2 4 4 2 4\\n\", \"3\\n3 3 2\\n\", \"15\\n1 2 2 1 2 3 2 1 2 1 1 1 2 1 1\\n\", \"172\\n2 2 2 0 1 3 2 1 0 3 3 1 0 1 2 3 4 2 2 4 2 1 4 0 3 2 2 3 3 3 0 0 3 1 1 0 1 2 2 0 1 4 4 0 3 3 2 0 1 4 4 1 4 2 2 3 0 1 2 2 1 1 4 4 4 4 0 1 0 2 4 0 2 0 0 2 2 1 4 2 2 2 2 2 0 2 3 0 2 1 0 2 1 0 2 2 0 2 2 0 2 2 2 1 1 0 2 1 2 1 0 2 2 0 2 2 3 2 4 2 4 3 2 3 1 2 2 4 0 2 0 2 2 1 0 1 2 1 4 1 0 3 2 2 1 0 0 2 0 4 2 2 0 0 4 1 3 2 1 1 0 2 3 2 0 2 2 2 2 2 3 0\\n\", \"10\\n2 3 3 1 3 1 3 2 2 4\\n\", \"10\\n1 1 1 2 1 2 2 1 2 1\\n\", \"5\\n4 4 3 3 1\\n\", \"3\\n1 4 4\\n\", \"14\\n4 2 4 4 0 4 4 0 1 0 0 4 3 4\\n\", \"10\\n3 4 2 2 1 1 3 1 1 2\\n\", \"20\\n4 1 1 1 4 2 3 3 2 1 1 4 4 3 1 1 2 4 2 3\\n\", \"11\\n2 2 2 2 0 2 2 2 2 2 2\\n\", \"20\\n4 4 2 4 3 2 3 1 4 1 1 4 1 4 3 4 4 3 3 3\\n\", \"20\\n4 1 4 4 2 1 4 3 2 3 1 1 2 2 2 4 4 2 4 2\\n\", \"2\\n2 3\\n\", \"16\\n3 3 3 1 3 0 1 4 4 4 1 4 3 1 1 4\\n\", \"13\\n2 1 2 2 1 0 1 2 1 1 1 1 2\\n\", \"200\\n4 1 1 4 3 1 1 3 1 1 1 4 3 3 3 2 3 3 1 3 3 4 4 2 2 2 3 1 2 2 2 3 1 1 3 2 2 4 1 3 4 3 2 4 2 2 4 2 2 3 4 2 3 2 2 1 2 4 4 2 4 4 2 3 2 4 1 4 2 1 3 4 1 3 1 1 2 1 4 1 3 3 3 4 1 4 4 1 4 4 2 3 1 3 3 2 2 1 4 2 4 4 3 3 3 1 3 4 3 1 1 1 1 4 2 1 2 3 2 2 2 3 2 1 2 1 1 1 2 4 1 3 3 3 2 3 3 2 3 4 4 3 3 4 3 2 1 4 1 4 2 1 3 2 4 4 1 4 1 1 1 3 2 3 4 2 2 4 1 4 4 4 4 3 1 3 1 4 3 2 1 2 1 1 2 4 1 3 3 4 4 2 2 4 4 3 2 1 2 4\\n\", \"13\\n2 2 0 4 2 2 2 2 2 1 2 2 2\\n\", \"13\\n1 1 1 2 1 1 4 1 3 1 1 1 0\\n\", \"10\\n2 2 2 0 0 0 0 0 2 2\\n\", \"4\\n3 3 3 2\\n\", \"120\\n1 1 1 1 1 1 1 4 4 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 4 1 1 4 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 1 1 1 2 4 1 1 3 1 1 1 2 1 0 3 1 1 1 2 1 4 1 1 1 1 1 1 1 1 1 1\\n\", \"6\\n2 2 2 4 4 4\\n\", \"27\\n0 2 4 1 4 2 1 2 3 4 2 4 1 2 3 2 3 2 2 1 0 4 3 0 3 0 1\\n\", \"146\\n1 1 1 1 1 4 1 1 0 1 4 4 1 4 1 1 1 1 1 4 1 1 1 1 1 1 1 4 1 1 1 1 4 1 4 1 1 1 0 1 4 1 4 1 4 4 1 1 1 1 1 1 1 1 1 4 4 1 1 4 1 4 4 4 1 1 4 4 1 4 1 1 1 1 0 1 1 1 1 1 1 4 1 4 1 1 4 1 1 4 4 4 1 1 4 1 1 1 1 1 1 1 4 1 1 1 4 1 4 1 1 1 1 1 1 1 4 1 1 4 4 4 1 1 1 1 1 1 1 4 1 1 1 1 4 1 4 1 1 1 4 4 4 4 1 1\\n\", \"30\\n1 1 1 3 3 4 0 1 1 1 1 1 1 3 0 0 0 1 1 1 1 3 1 1 1 1 3 1 1 1\\n\", \"11\\n1 1 1 1 1 1 1 1 1 1 1\\n\", \"115\\n2 2 2 2 4 2 2 2 2 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 4 2 4 2 4 2 2 2 2 2 2 2 2 2 2 2 4 4 3 2 2 2 2 2 2 2 4 2 2 2 3 2 2 2 2 2 2 4 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 3 2 2 2 2 2 4 4 4 2 2\\n\", \"32\\n1 4 4 3 1 4 4 4 1 1 1 1 1 4 1 1 1 4 1 1 1 1 2 1 1 4 4 1 1 1 1 4\\n\", \"4\\n2 2 2 2\\n\", \"21\\n0 3 2 3 0 2 3 4 3 0 1 3 2 2 3 3 3 0 2 2 0\\n\", \"9\\n1 1 1 2 1 1 1 1 1\\n\", \"20\\n4 2 3 3 1 3 2 2 1 4 4 4 2 1 4 2 1 3 4 4\\n\", \"166\\n2 3 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 3 2 2 2 2 2 2 2 2 2 4 2 2 2 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 2 2 2 2 2 2 2 2 2 3 2 0 2 0 3 2 2 2 0 2 0 2 2 2 2 2 2 3 0 2 2 2 2 2 3 3 2 2 2 3 2 2 2 3 3 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 3 2 2 2 2\\n\", \"3\\n1 1 1\\n\", \"3\\n2 4 3\\n\", \"2\\n1 0\\n\", \"14\\n1 0 0 1 2 1 0 1 1 1 1 1 3 0\\n\", \"19\\n2 2 3 2 0 0 1 1 2 0 0 2 1 2 2 2 0 2 0\\n\", \"5\\n1 2 1 1 1\\n\", \"165\\n1 1 1 1 1 1 1 1 0 2 2 2 1 1 1 1 1 4 4 1 1 2 2 1 2 1 2 2 2 1 2 2 3 1 1 2 1 1 2 2 4 1 2 2 2 4 1 1 1 4 2 2 1 1 1 1 1 2 1 1 1 2 1 1 1 1 4 2 2 1 1 1 1 2 1 1 1 1 2 2 1 1 2 1 1 1 1 2 2 1 2 1 2 1 2 2 1 2 2 1 1 1 2 1 4 2 1 2 1 1 1 1 2 3 2 1 2 1 1 2 1 1 1 1 1 2 1 2 1 1 0 1 2 1 1 1 1 1 3 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 2 3 4 1 1 1\\n\", \"48\\n1 3 1 1 1 1 1 1 2 1 1 2 1 1 4 1 1 1 2 2 2 1 3 1 1 1 1 2 1 1 2 1 1 1 1 1 3 0 2 3 1 1 3 1 0 1 2 1\\n\", \"197\\n1 4 4 4 1 4 1 1 0 1 4 4 1 1 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 4 1 1 1 1 1 4 1 1 1 2 1 1 4 4 4 4 4 4 1 1 1 4 1 4 4 4 4 4 1 1 1 1 1 4 4 1 4 0 4 1 4 4 1 4 4 4 2 1 1 4 4 2 1 1 1 4 1 4 1 4 4 4 1 1 4 4 4 1 1 0 1 4 1 4 0 4 3 1 1 1 4 1 4 4 4 1 4 1 4 3 1 4 4 4 1 1 4 0 4 1 1 4 1 4 4 1 4 1 1 1 4 1 4 1 1 3 4 1 4 4 1 1 1 1 4 1 0 3 4 1 1 0 1 4 4 1 4 4 1 4 4 1 1 0 2 1 4 1 4 1 1 1 1 1 4 4 1 1 0 4 2 4 1 4 1 4 4\\n\", \"198\\n1 2 1 2 2 1 2 1 1 1 3 2 1 1 2 1 2 2 1 1 1 4 1 1 1 1 0 1 1 1 1 4 1 1 3 1 2 1 1 1 2 1 2 0 1 1 1 1 1 1 1 1 1 2 4 4 1 0 1 1 1 1 1 1 1 1 2 1 1 1 4 0 1 2 1 0 1 1 2 2 1 1 1 1 3 2 2 2 1 1 4 1 2 2 2 1 1 2 2 1 2 2 2 1 1 1 1 3 1 3 1 1 0 1 4 1 2 2 1 1 1 2 2 1 1 1 1 3 2 1 2 1 1 2 1 2 1 2 1 0 4 1 2 1 1 1 1 3 1 1 2 0 1 1 1 1 1 3 2 1 2 1 1 0 1 1 3 1 1 2 1 1 1 1 1 1 4 4 1 1 0 1 1 1 2 1 1 1 3 0 2 1 2 1 1 1 1 1\\n\", \"81\\n2 2 2 3 2 3 2 2 2 2 2 3 2 2 2 2 2 2 0 2 4 2 3 4 2 3 2 3 2 0 2 2 0 2 2 3 2 2 4 3 3 2 2 2 2 2 2 2 3 2 2 2 2 2 2 1 3 2 2 3 2 0 2 0 2 2 2 2 2 2 4 0 2 3 2 4 2 2 2 2 2\\n\", \"10\\n3 4 1 3 1 2 2 2 2 2\\n\", \"200\\n2 1 1 2 2 2 2 1 1 2 2 2 1 1 2 2 2 2 1 1 1 2 2 2 2 2 2 1 2 2 1 1 1 1 2 1 2 2 1 2 2 2 2 1 2 2 1 1 1 1 2 2 1 1 1 1 1 2 2 2 2 1 2 1 2 2 2 2 1 1 1 2 0 2 2 2 2 1 1 1 1 1 1 2 2 2 1 2 2 2 1 2 2 2 1 1 1 2 2 1 1 1 1 2 2 1 2 1 1 1 2 2 1 1 2 2 2 1 2 2 0 1 2 1 1 2 2 2 1 2 2 1 1 1 2 2 2 1 2 1 2 1 2 1 1 2 2 1 1 1 1 1 2 2 1 1 1 1 1 2 1 2 2 1 1 1 1 1 1 2 2 1 1 1 1 2 2 1 1 1 2 2 2 2 1 1 1 1 1 1 2 1 1 2 2 1 1 2 1 0\\n\", \"177\\n2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 4 2 2 2 2 4 2 0 2 2 2 2 2 3 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 4 2 2 2 1 2 2 4 2 2 2 2 2 3 2 1 2 2 2 2 2 2 4 4 2 2 2 4 2 2 2 2 2 2 2 2 4 2 4 2 2 4 2 2 2 2 2 2 2 2 0 2 3 2 2 2 2 2 2 2 0 2 2 4 2 2 2 2 3 2 2\\n\", \"16\\n0 0 1 1 1 1 1 2 1 1 1 0 1 1 0 1\\n\", \"138\\n3 1 3 1 3 3 1 1 1 1 1 1 1 3 3 1 1 1 3 3 1 1 3 1 1 1 1 1 1 1 3 3 3 1 3 1 1 1 1 1 3 1 1 3 1 3 1 3 1 1 1 1 3 1 3 1 1 3 1 1 1 3 1 1 1 1 1 1 1 1 3 1 1 1 1 3 1 3 1 3 3 3 3 3 3 1 1 1 3 1 1 3 1 1 1 1 1 1 1 1 3 1 1 3 3 1 3 3 1 3 1 1 1 3 1 1 1 1 1 1 3 1 1 1 1 3 1 1 1 3 1 1 3 1 1 3 1 1\\n\", \"29\\n3 3 2 0 1 1 1 2 2 2 1 3 2 0 2 3 3 2 2 3 1 2 2 2 1 2 2 2 4\\n\", \"172\\n2 2 2 0 1 3 2 1 0 3 3 1 0 1 2 3 4 2 2 4 2 1 4 0 3 2 2 3 3 3 0 0 3 1 1 0 1 2 2 0 1 4 4 0 3 3 2 0 1 4 4 1 4 2 2 3 0 1 2 2 1 1 4 4 4 4 0 1 0 2 4 0 2 0 0 2 2 1 4 2 2 2 2 2 0 2 3 0 2 1 0 2 1 0 2 2 0 2 2 0 2 2 2 1 1 0 2 1 2 1 0 2 2 0 2 2 3 2 4 0 4 3 2 3 1 2 2 4 0 2 0 2 2 1 0 1 2 1 4 1 0 3 2 2 1 0 0 2 0 4 2 2 0 0 4 1 3 2 1 1 0 2 3 2 0 2 2 2 2 2 3 0\\n\", \"120\\n1 1 1 1 1 1 1 4 4 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 4 1 1 4 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 1 1 1 1 2 4 1 1 3 1 1 2 2 1 0 3 1 1 1 2 1 4 1 1 1 1 1 1 1 1 1 1\\n\", \"146\\n1 1 1 1 1 4 1 1 0 1 4 4 1 4 1 1 1 1 1 4 2 1 1 1 1 1 1 4 1 1 1 1 4 1 4 1 1 1 0 1 4 1 4 1 4 4 1 1 1 1 1 1 1 1 1 4 4 1 1 4 1 4 4 4 1 1 4 4 1 4 1 1 1 1 0 1 1 1 1 1 1 4 1 4 1 1 4 1 1 4 4 4 1 1 4 1 1 1 1 1 1 1 4 1 1 1 4 1 4 1 1 1 1 1 1 1 4 1 1 4 4 4 1 1 1 1 1 1 1 4 1 1 1 1 4 1 4 1 1 1 4 4 4 4 1 1\\n\", \"30\\n1 1 1 3 3 3 0 1 1 1 1 1 1 3 0 0 0 1 1 1 1 3 1 1 1 1 3 1 1 1\\n\", \"115\\n2 2 2 2 4 2 2 2 2 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 4 2 4 2 4 2 2 2 2 2 2 2 2 2 2 2 4 4 3 2 2 2 2 2 2 2 4 2 2 2 3 2 2 2 2 3 2 4 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 3 2 2 2 2 2 4 4 4 2 2\\n\", \"20\\n4 3 4 2 1 1 3 1 4 2 0 4 3 3 4 3 1 1 1 3\\n\", \"13\\n4 1 1 4 1 1 1 1 1 0 1 1 1\\n\", \"6\\n2 2 3 2 2 4\\n\", \"3\\n3 4 1\\n\", \"29\\n3 1 3 3 0 2 2 3 3 2 0 4 3 2 3 0 3 3 0 2 2 2 3 2 0 3 2 2 3\\n\", \"23\\n2 3 1 1 1 2 4 3 2 2 3 3 4 1 4 2 4 1 4 2 3 1 1\\n\", \"9\\n1 1 1 1 3 3 3 3 2\\n\", \"21\\n1 1 3 1 0 3 3 3 3 0 1 3 0 3 1 2 1 3 2 0 0\\n\", \"19\\n2 4 4 2 0 0 1 4 1 0 2 2 4 2 0 1 1 2 4\\n\", \"28\\n2 0 4 2 3 4 0 1 4 3 0 3 0 3 2 3 2 4 1 2 4 3 3 3 0 1 0 1\\n\", \"17\\n3 3 1 0 1 3 1 1 0 3 0 2 2 2 3 2 2\\n\", \"10\\n2 2 2 3 4 1 3 4 4 4\\n\", \"141\\n2 1 1 1 1 1 4 2 3 1 1 1 1 1 1 4 1 1 1 1 1 1 1 4 4 1 1 1 1 2 1 4 1 1 1 1 1 1 1 1 1 4 1 1 1 1 1 2 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 3 1 1 1 1 1 4 4 1 3 4 1 1 1 1 1 1 1 1 1 4 2 1 0 1 1 4 1 1 1 1 2 1 0 1 1 2 1 1 1 1 4 4 1 2 4 4 1 1 3 1 1 1 3 1 0 4 4 1 1 1 4 1 1 1 1 1 1 2 0 1 0 0 1 0 4\\n\", \"17\\n1 1 4 1 1 0 1 1 1 1 0 2 0 1 0 0 1\\n\", \"15\\n4 0 1 0 0 4 0 1 0 4 1 4 4 1 0\\n\", \"24\\n4 2 4 3 1 3 4 1 3 4 2 4 0 2 3 4 1 1 4 3 1 0 2 4\\n\", \"7\\n1 1 1 3 3 1 3\\n\", \"1\\n2\\n\", \"13\\n2 1 2 2 3 4 0 2 2 0 2 2 2\\n\", \"17\\n0 4 3 0 2 2 4 2 4 4 2 1 2 1 0 0 0\\n\", \"15\\n0 2 4 1 0 4 4 2 4 4 1 2 4 2 2\\n\", \"20\\n0 4 4 0 0 0 2 3 3 3 2 0 3 0 3 2 4 4 2 4\\n\", \"3\\n3 0 2\\n\", \"15\\n1 2 2 1 2 3 2 1 2 2 1 1 2 1 1\\n\", \"10\\n2 3 3 1 3 1 0 2 2 4\\n\", \"10\\n1 1 1 2 1 2 4 1 2 1\\n\", \"10\\n4 4 2 2 1 1 3 1 1 2\\n\", \"20\\n4 1 1 1 4 2 3 3 2 1 1 4 4 3 1 0 2 4 2 3\\n\", \"11\\n2 2 0 2 0 2 2 2 2 2 2\\n\", \"20\\n4 4 2 4 4 2 3 1 4 1 1 4 1 4 3 4 4 3 3 3\\n\", \"20\\n1 1 4 4 2 1 4 3 2 3 1 1 2 2 2 4 4 2 4 2\\n\", \"2\\n1 3\\n\", \"13\\n2 1 2 2 1 0 1 2 1 1 2 1 2\\n\", \"13\\n1 1 1 2 0 1 4 1 3 1 1 1 0\\n\", \"6\\n2 2 4 4 4 4\\n\", \"27\\n0 2 4 1 4 2 1 2 3 4 2 4 1 2 3 2 3 2 2 2 0 4 3 0 3 0 1\\n\", \"11\\n1 1 1 2 1 1 1 1 1 1 1\\n\", \"3\\n4 1 1\\n\", \"4\\n0 3 0 4\\n\", \"5\\n1 2 2 4 3\\n\"], \"outputs\": [\"2\\n\", \"2\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"3\\n\", \"69\\n\", \"5\\n\", \"4\\n\", \"6\\n\", \"6\\n\", \"6\\n\", \"4\\n\", \"4\\n\", \"7\\n\", \"7\\n\", \"5\\n\", \"5\\n\", \"5\\n\", \"4\\n\", \"5\\n\", \"5\\n\", \"4\\n\", \"4\\n\", \"6\\n\", \"5\\n\", \"4\\n\", \"5\\n\", \"5\\n\", \"7\\n\", \"1\\n\", \"7\\n\", \"4\\n\", \"8\\n\", \"8\\n\", \"8\\n\", \"8\\n\", \"6\\n\", \"6\\n\", \"7\\n\", \"9\\n\", \"7\\n\", \"11\\n\", \"12\\n\", \"8\\n\", \"14\\n\", \"14\\n\", \"24\\n\", \"24\\n\", \"84\\n\", \"69\\n\", \"103\\n\", \"93\\n\", \"53\\n\", \"69\\n\", \"61\\n\", \"62\\n\", \"38\\n\", \"65\\n\", \"68\\n\", \"97\\n\", \"50\\n\", \"100\\n\", \"4\\n\", \"5\\n\", \"6\\n\", \"8\\n\", \"7\\n\", \"2\\n\", \"2\\n\", \"-1\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"2\\n\", \"2\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"4\\n\", \"4\\n\", \"2\\n\", \"-1\\n\", \"-1\\n\", \"2\\n\", \"2\\n\", \"0\\n\", \"4\\n\", \"93\\n\", \"6\\n\", \"-1\\n\", \"2\\n\", \"2\\n\", \"-1\\n\", \"6\\n\", \"9\\n\", \"-1\\n\", \"6\\n\", \"8\\n\", \"61\\n\", \"84\\n\", \"2\\n\", \"5\\n\", \"24\\n\", \"2\\n\", \"69\\n\", \"5\\n\", \"97\\n\", \"4\\n\", \"2\\n\", \"7\\n\", \"7\\n\", \"38\\n\", \"5\\n\", \"3\\n\", \"5\\n\", \"5\\n\", \"5\\n\", \"5\\n\", \"2\\n\", \"100\\n\", \"103\\n\", \"8\\n\", \"-1\\n\", \"69\\n\", \"24\\n\", \"8\\n\", \"11\\n\", \"4\\n\", \"62\\n\", \"2\\n\", \"5\\n\", \"4\\n\", \"2\\n\", \"12\\n\", \"0\\n\", \"-1\\n\", \"7\\n\", \"4\\n\", \"5\\n\", \"1\\n\", \"4\\n\", \"2\\n\", \"8\\n\", \"53\\n\", \"3\\n\", \"6\\n\", \"1\\n\", \"2\\n\", \"1\\n\", \"4\\n\", \"6\\n\", \"8\\n\", \"4\\n\", \"6\\n\", \"-1\\n\", \"4\\n\", \"7\\n\", \"50\\n\", \"7\\n\", \"7\\n\", \"4\\n\", \"2\\n\", \"69\\n\", \"2\\n\", \"7\\n\", \"68\\n\", \"14\\n\", \"8\\n\", \"65\\n\", \"14\\n\", \"4\\n\", \"5\\n\", \"6\\n\", \"5\\n\", \"93\\n\", \"2\\n\", \"1\\n\", \"-1\\n\", \"6\\n\", \"7\\n\", \"3\\n\", \"85\\n\", \"24\\n\", \"68\\n\", \"97\\n\", \"38\\n\", \"4\\n\", \"99\\n\", \"103\\n\", \"8\\n\", \"63\\n\", \"12\\n\", \"53\\n\", \"69\\n\", \"67\\n\", \"14\\n\", \"64\\n\", \"5\\n\", \"7\\n\", \"3\\n\", \"1\\n\", \"7\\n\", \"7\\n\", \"3\\n\", \"5\\n\", \"6\\n\", \"5\\n\", \"6\\n\", \"3\\n\", \"68\\n\", \"7\\n\", \"3\\n\", \"5\\n\", \"3\\n\", \"-1\\n\", \"6\\n\", \"4\\n\", \"4\\n\", \"3\\n\", \"-1\\n\", \"7\\n\", \"3\\n\", \"5\\n\", \"4\\n\", \"6\\n\", \"6\\n\", \"4\\n\", \"7\\n\", \"1\\n\", \"6\\n\", \"6\\n\", \"2\\n\", \"8\\n\", \"7\\n\", \"2\\n\", \"0\\n\", \"2\\n\"]}", "source": "taco"}
|
A team of students from the city S is sent to the All-Berland Olympiad in Informatics. Traditionally, they go on the train. All students have bought tickets in one carriage, consisting of n compartments (each compartment has exactly four people). We know that if one compartment contain one or two students, then they get bored, and if one compartment contain three or four students, then the compartment has fun throughout the entire trip.
The students want to swap with other people, so that no compartment with students had bored students. To swap places with another person, you need to convince him that it is really necessary. The students can not independently find the necessary arguments, so they asked a sympathetic conductor for help. The conductor can use her life experience to persuade any passenger to switch places with some student.
However, the conductor does not want to waste time persuading the wrong people, so she wants to know what is the minimum number of people necessary to persuade her to change places with the students. Your task is to find the number.
After all the swaps each compartment should either have no student left, or have a company of three or four students.
-----Input-----
The first line contains integer n (1 ≤ n ≤ 10^6) — the number of compartments in the carriage. The second line contains n integers a_1, a_2, ..., a_{n} showing how many students ride in each compartment (0 ≤ a_{i} ≤ 4). It is guaranteed that at least one student is riding in the train.
-----Output-----
If no sequence of swapping seats with other people leads to the desired result, print number "-1" (without the quotes). In another case, print the smallest number of people you need to persuade to swap places.
-----Examples-----
Input
5
1 2 2 4 3
Output
2
Input
3
4 1 1
Output
2
Input
4
0 3 0 4
Output
0
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"5 82\\n22 11 6 7 13\", \"10 100000\\n13715 50001 50002 50003 50004 50005 50006 50007 50008 50009\", \"2 19\\n3 11\", \"5 134\\n22 11 6 7 13\", \"10 100000\\n13715 50001 50002 50003 50004 50005 50006 50532 50008 50009\", \"10 000000\\n13715 50001 50002 50003 50004 50005 50006 50532 50008 50009\", \"10 100000\\n13715 50001 13306 50003 50004 50005 50006 50532 50008 50009\", \"5 82\\n22 11 11 5 13\", \"2 17\\n3 7\", \"5 82\\n27 11 6 7 13\", \"10 100000\\n13715 50001 50002 50003 50004 53429 50006 50007 50008 50009\", \"5 134\\n22 11 3 7 13\", \"10 100000\\n13715 50001 50002 50003 50004 50005 50006 50532 49493 50009\", \"5 193\\n18 11 6 7 13\", \"10 100000\\n13715 50001 13306 50003 50004 50005 50006 50532 50008 36071\", \"10 100000\\n25030 50001 50002 50003 50004 53429 50006 50007 50008 50009\", \"2 12\\n6 11\", \"10 100000\\n13715 50001 50002 50003 5405 50005 50006 50532 49493 50009\", \"5 193\\n18 13 6 7 13\", \"10 100000\\n13715 50001 13306 50003 50004 50005 50006 50532 97937 36071\", \"5 193\\n5 13 6 7 13\", \"10 100000\\n13715 50001 13306 50003 50004 50005 50006 86630 97937 36071\", \"5 193\\n5 13 6 5 13\", \"10 100000\\n13715 50001 13306 50003 50004 50005 50006 86630 62164 36071\", \"2 20\\n6 3\", \"5 193\\n5 13 7 5 13\", \"10 100000\\n13715 50001 13306 50003 50004 59986 50006 86630 62164 36071\", \"5 193\\n5 13 7 5 4\", \"10 100000\\n13715 50001 13306 50003 50004 59986 50006 110740 62164 36071\", \"5 193\\n5 13 13 5 4\", \"10 100000\\n13715 50001 13306 50003 50004 59986 50006 110740 62439 36071\", \"5 278\\n5 13 13 5 4\", \"10 100000\\n13715 50001 13306 50003 50004 59986 50006 57622 62439 36071\", \"10 100001\\n13715 50001 13306 50003 50004 59986 50006 57622 62439 36071\", \"10 100001\\n13715 64565 13306 50003 50004 59986 50006 57622 62439 36071\", \"10 100001\\n13715 64565 13306 50003 50004 59986 50006 23347 62439 36071\", \"10 100001\\n13715 64565 14615 50003 50004 59986 50006 23347 62439 36071\", \"10 100001\\n13715 64565 14615 50003 50004 59986 79355 23347 62439 36071\", \"10 100001\\n13715 64565 14615 50003 55957 59986 79355 23347 62439 36071\", \"10 100001\\n13715 64565 14615 50003 55957 59986 79355 23347 62439 46336\", \"10 100001\\n13715 64565 14615 50003 20289 59986 79355 23347 62439 46336\", \"10 100001\\n13715 64565 14615 43639 20289 59986 79355 23347 62439 46336\", \"10 100001\\n13715 64565 14615 43639 20289 59986 79355 23347 10116 46336\", \"5 147\\n22 11 6 7 13\", \"10 100000\\n13715 50001 50002 50003 50004 50005 70469 50007 50008 50009\", \"5 35\\n22 11 6 7 13\", \"10 100000\\n13715 50001 50002 50003 28633 50005 50006 50532 50008 50009\", \"10 001000\\n13715 50001 50002 50003 50004 50005 50006 50532 50008 50009\", \"10 100000\\n13715 50001 22339 50003 50004 50005 50006 50532 50008 50009\", \"5 29\\n22 11 11 5 13\", \"5 82\\n27 11 6 4 13\", \"10 100000\\n13715 50001 50002 50003 50004 53429 67402 50007 50008 50009\", \"10 100000\\n13715 19943 50002 50003 50004 50005 50006 50532 49493 50009\", \"10 100000\\n13715 50001 13306 50003 50004 50005 35293 50532 50008 36071\", \"10 100000\\n3020 50001 50002 50003 50004 53429 50006 50007 50008 50009\", \"10 100000\\n2576 50001 50002 50003 5405 50005 50006 50532 49493 50009\", \"10 100000\\n13715 40609 13306 50003 50004 50005 50006 50532 97937 36071\", \"10 100000\\n13715 50001 13306 50003 50004 79705 50006 86630 97937 36071\", \"5 193\\n5 13 6 6 13\", \"10 100000\\n13715 50001 13306 50003 50004 83534 50006 86630 62164 36071\", \"5 193\\n5 13 14 5 13\", \"10 100000\\n13715 50001 13306 95131 50004 59986 50006 86630 62164 36071\", \"10 100000\\n13715 50001 13306 50003 50004 59986 50006 110740 49261 36071\", \"10 100000\\n13715 87116 13306 50003 50004 59986 50006 57622 62439 36071\", \"5 278\\n5 25 13 5 8\", \"10 100001\\n13715 50001 13306 50003 2167 59986 50006 57622 62439 36071\", \"10 000001\\n13715 64565 13306 50003 50004 59986 50006 57622 62439 36071\", \"10 100001\\n13715 64565 13306 82856 50004 59986 50006 23347 62439 36071\", \"10 100001\\n13715 64565 14615 50003 50004 59986 68712 23347 62439 36071\", \"10 100001\\n13715 64565 14615 50003 50004 59986 79355 25417 62439 36071\", \"10 100001\\n13715 59381 14615 50003 55957 59986 79355 23347 62439 36071\", \"10 100000\\n13715 64565 14615 50003 55957 59986 79355 23347 62439 46336\", \"10 100001\\n13715 64565 14615 95438 20289 59986 79355 23347 62439 46336\", \"10 100001\\n13715 64565 14615 43639 20289 59986 79355 23347 62439 69981\", \"10 100001\\n13715 64565 14615 72144 20289 59986 79355 23347 10116 46336\", \"5 147\\n22 9 6 7 13\", \"10 100000\\n13715 50001 50002 50003 50004 50005 70469 50007 50008 54425\", \"5 35\\n22 11 7 7 13\", \"10 100000\\n13715 50001 50002 50003 28633 50005 73522 50532 50008 50009\", \"10 100000\\n13715 50001 22339 50003 11265 50005 50006 50532 50008 50009\", \"5 58\\n22 11 11 5 13\", \"5 82\\n27 11 7 4 13\", \"10 100000\\n13715 50001 50002 50003 50004 55698 67402 50007 50008 50009\", \"5 97\\n22 11 6 7 13\", \"10 100000\\n13715 19943 50002 50003 92084 50005 50006 50532 49493 50009\", \"10 100000\\n3020 50001 50002 50003 50004 53429 50006 50007 50008 68870\", \"10 100000\\n2576 50001 50002 50003 2080 50005 50006 50532 49493 50009\", \"10 100000\\n13715 40609 13306 50003 30772 50005 50006 50532 97937 36071\", \"10 100000\\n13715 61924 13306 50003 50004 79705 50006 86630 97937 36071\", \"5 193\\n5 11 6 6 13\", \"10 100000\\n13715 50001 13306 50003 99466 83534 50006 86630 62164 36071\", \"10 100000\\n13715 50001 13306 95131 50004 4964 50006 86630 62164 36071\", \"10 100000\\n13715 50001 13306 64131 50004 59986 50006 215588 62439 36071\", \"10 100000\\n13715 87116 9086 50003 50004 59986 50006 57622 62439 36071\", \"5 278\\n5 25 23 5 8\", \"10 100001\\n13715 64565 13306 82856 65920 59986 50006 23347 62439 36071\", \"10 100001\\n13715 64565 14615 50003 50004 8510 68712 23347 62439 36071\", \"10 100001\\n13715 83247 14615 50003 50004 59986 79355 25417 62439 36071\", \"10 100001\\n13715 59381 14615 50003 55957 59986 79355 14619 62439 36071\", \"10 100000\\n13715 64565 14615 50003 55957 59986 79355 23347 62439 67118\", \"5 82\\n22 11 6 5 13\", \"10 100000\\n50000 50001 50002 50003 50004 50005 50006 50007 50008 50009\", \"2 19\\n3 7\"], \"outputs\": [\"516\\n\", \"353097390\\n\", \"3\\n\", \"264\\n\", \"162585390\\n\", \"0\\n\", \"219654823\\n\", \"168\\n\", \"2\\n\", \"456\\n\", \"110596277\\n\", \"192\\n\", \"717518608\\n\", \"210\\n\", \"452642420\\n\", \"330531857\\n\", \"1\\n\", \"325639951\\n\", \"342\\n\", \"862925634\\n\", \"272\\n\", \"713224528\\n\", \"200\\n\", \"794462274\\n\", \"4\\n\", \"336\\n\", \"465753474\\n\", \"198\\n\", \"491699060\\n\", \"248\\n\", \"380819060\\n\", \"208\\n\", \"552337147\\n\", \"555965947\\n\", \"268359860\\n\", \"655749380\\n\", \"298407839\\n\", \"971005919\\n\", \"887997119\\n\", \"91579345\\n\", \"893585471\\n\", \"232201898\\n\", \"359738082\\n\", \"324\\n\", \"904383171\\n\", \"246\\n\", \"344627665\\n\", \"628799979\\n\", \"684283345\\n\", \"312\\n\", \"96\\n\", \"774835011\\n\", \"294148027\\n\", \"115183168\\n\", \"447191645\\n\", \"535721259\\n\", \"761991067\\n\", \"835757008\\n\", \"136\\n\", \"527527241\\n\", \"216\\n\", \"892463561\\n\", \"639926295\\n\", \"886804653\\n\", \"240\\n\", \"164495019\\n\", \"3628800\\n\", \"919511227\\n\", \"295686239\\n\", \"748580138\\n\", \"631168799\\n\", \"87950545\\n\", \"271101119\\n\", \"367458865\\n\", \"101537371\\n\", \"276\\n\", \"301905098\\n\", \"180\\n\", \"983212298\\n\", \"879536472\\n\", \"306\\n\", \"120\\n\", \"951460298\\n\", \"144\\n\", \"812340667\\n\", \"178297565\\n\", \"11080946\\n\", \"513726715\\n\", \"411829001\\n\", \"134\\n\", \"381515415\\n\", \"606206671\\n\", \"348163053\\n\", \"258267756\\n\", \"288\\n\", \"871088420\\n\", \"380911120\\n\", \"757094712\\n\", \"583755004\\n\", \"904817112\\n\", \"288\", \"279669259\", \"3\"]}", "source": "taco"}
|
Snuke has a blackboard and a set S consisting of N integers. The i-th element in S is S_i.
He wrote an integer X on the blackboard, then performed the following operation N times:
* Choose one element from S and remove it.
* Let x be the number written on the blackboard now, and y be the integer removed from S. Replace the number on the blackboard with x \bmod {y}.
There are N! possible orders in which the elements are removed from S. For each of them, find the number that would be written on the blackboard after the N operations, and compute the sum of all those N! numbers modulo 10^{9}+7.
Constraints
* All values in input are integers.
* 1 \leq N \leq 200
* 1 \leq S_i, X \leq 10^{5}
* S_i are pairwise distinct.
Input
Input is given from Standard Input in the following format:
N X
S_1 S_2 \ldots S_{N}
Output
Print the answer.
Examples
Input
2 19
3 7
Output
3
Input
5 82
22 11 6 5 13
Output
288
Input
10 100000
50000 50001 50002 50003 50004 50005 50006 50007 50008 50009
Output
279669259
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"1000000000 10000000 10000000\\n\", \"646139320 570870045 9580639\\n\", \"458000643 743974603 152040411\\n\", \"999999999 1000000000 1\\n\", \"167035009 877444310 205461190\\n\", \"999999123 999999789 123456789\\n\", \"192837483 829387483 828374\\n\", \"628145517 207579013 1361956\\n\", \"9467291 727123763 403573724\\n\", \"999524524 888524524 6\\n\", \"100 100 150\\n\", \"1000000000 1000000000 999999999\\n\", \"456517317 162733265 614608449\\n\", \"4 6 3\\n\", \"6874 8974 3245\\n\", \"5 4 3\\n\", \"127860890 61402893 158176573\\n\", \"732553408 300206285 785986539\\n\", \"98723848 8238748 82838\\n\", \"6 7 2\\n\", \"7 8 9\\n\", \"61263305 484027667 178509023\\n\", \"888999999 999999444 7\\n\", \"1 1 1\\n\", \"1000000000 1000000000 2000000000\\n\", \"158398860 751354014 528156707\\n\", \"899374334 631265401 296231663\\n\", \"6 7 1\\n\", \"5 5 5\\n\", \"599399444 599999994 897254524\\n\", \"793692317 55434271 489726670\\n\", \"1000000000 1000000000 1999999998\\n\", \"482738478 493948384 502919283\\n\", \"6 6 9\\n\", \"1000000000 1000000000 220000000\\n\", \"999882937 982983748 999999888\\n\", \"896205951 132099861 775142615\\n\", \"537850353 901329639 210461043\\n\", \"989872444 999283444 977999524\\n\", \"999872837 979283748 987837524\\n\", \"4 5 6\\n\", \"307178253 337246325 118054687\\n\", \"98152103 326402540 762888636\\n\", \"999872524 989283524 977999444\\n\", \"940563716 558212775 841082556\\n\", \"999999789 999999123 52452444\\n\", \"6 4 5\\n\", \"491747710 798571511 520690250\\n\", \"6 4 6\\n\", \"500000002 500000002 1000000000\\n\", \"2 2 2\\n\", \"2 1 1\\n\", \"1 1 2\\n\", \"644505509 896162464 150625750\\n\", \"98283 999283848 23\\n\", \"6 7 5\\n\", \"4 6 4\\n\", \"298238388 998888999 1000000000\\n\", \"789529529 444524524 888524444\\n\", \"100 100 100\\n\", \"909420688 506507264 590064714\\n\", \"444444444 524444444 524\\n\", \"1000 1000 1000\\n\", \"1 1 1000000000\\n\", \"570497240 614794872 29523792\\n\", \"904237002 706091348 905203770\\n\", \"999888524 999995249 52424\\n\", \"186969586 883515281 376140463\\n\", \"999995244 999852424 52999\\n\", \"496148000 579113529 26389630\\n\", \"983748524 23 2\\n\", \"979882937 982983748 988254444\\n\", \"70301174 837151741 925801173\\n\", \"979283524 999872524 987524524\\n\", \"1000000000 1000000000 123456\\n\", \"19344368 457641319 555144413\\n\", \"882264705 164556874 37883251\\n\", \"902071051 285845006 656585276\\n\", \"10 10 11\\n\", \"10 10 2\\n\", \"789204467 643215696 799313373\\n\", \"181457955 806956092 555253432\\n\", \"987283748 999283748 589766888\\n\", \"1000000000 1000000000 1\\n\", \"789789789 777888999 999999999\\n\", \"1000000000 999999999 3\\n\", \"1000000000 1000000000 999000111\\n\", \"12345 123456789 123456789\\n\", \"1000000000 10000000 10001000\\n\", \"646139320 842734588 9580639\\n\", \"616005340 743974603 152040411\\n\", \"999999999 1000010000 1\\n\", \"167035009 877444310 207119422\\n\", \"688159537 999999789 123456789\\n\", \"192837483 829387483 60512\\n\", \"628145517 102897974 1361956\\n\", \"9467291 1427564804 403573724\\n\", \"100 100 94\\n\", \"1000000000 1000000000 761701863\\n\", \"456517317 31347886 614608449\\n\", \"4 3 3\\n\", \"6874 6694 3245\\n\", \"9 4 3\\n\", \"127860890 50575986 158176573\\n\", \"98723848 8238748 80213\\n\", \"6 7 4\\n\", \"86802768 484027667 178509023\\n\", \"888999999 999999444 2\\n\", \"158398860 751354014 742510666\\n\", \"899374334 631265401 392822730\\n\", \"6 14 2\\n\", \"5 7 5\\n\", \"599399444 599999994 153097743\\n\", \"793692317 55434271 655572542\\n\", \"482738478 449405451 502919283\\n\", \"896205951 88208737 775142615\\n\", \"537850353 901329639 84600826\\n\", \"4 5 5\\n\", \"307178253 337246325 130143250\\n\", \"716979931 558212775 841082556\\n\", \"999999789 999999123 48997920\\n\", \"491747710 798571511 468579508\\n\", \"644505509 955070886 150625750\\n\", \"98283 1617354632 23\\n\", \"789529529 655520456 888524444\\n\", \"909420688 506507264 61212266\\n\", \"444444444 524444444 229\\n\", \"1000 1000 0000\\n\", \"570497240 614794872 45838744\\n\", \"904237002 569903669 905203770\\n\", \"186969586 1155280313 376140463\\n\", \"732553408 300206285 1466919113\\n\", \"7 8 12\\n\", \"2 1 2\\n\", \"1000000000 1000000001 2000000000\\n\", \"0000000000 1000000000 1999999998\\n\", \"6 6 15\\n\", \"98152103 326402540 1475251111\\n\", \"999872524 989283524 1828655256\\n\", \"6 5 5\\n\", \"6 4 7\\n\", \"500000002 500000002 1000010000\\n\", \"2 2 4\\n\", \"1 2 1\\n\", \"6 2 5\\n\", \"4 6 5\\n\", \"298238388 998888999 1100000000\\n\", \"110 100 100\\n\", \"1 2 1000000000\\n\", \"6 4 2\\n\", \"2 3 4\\n\", \"3 4 1\\n\"], \"outputs\": [\"990000000\\n\", \"38248293015\\n\", \"2231923809\\n\", \"499999999500000000\\n\", \"668140036\\n\", \"7999998312\\n\", \"193030320483\\n\", \"95693924993\\n\", \"9467291\\n\", \"126871721067257708\\n\", \"1\\n\", \"1000000000\\n\", \"1\\n\", \"6\\n\", \"17948\\n\", \"5\\n\", \"2\\n\", \"5\\n\", \"9812348868\\n\", \"14\\n\", \"2\\n\", \"122526610\\n\", \"111124937645000070\\n\", \"-1\\n\", \"-1\\n\", \"158398860\\n\", \"1893796203\\n\", \"21\\n\", \"2\\n\", \"2\\n\", \"55434271\\n\", \"1\\n\", \"53\\n\", \"1\\n\", \"4000000000\\n\", \"8404\\n\", \"132099861\\n\", \"2151401412\\n\", \"999283444\\n\", \"979283748\\n\", \"1\\n\", \"674492650\\n\", \"-1\\n\", \"999872524\\n\", \"558212775\\n\", \"18999995991\\n\", \"4\\n\", \"491747710\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"3584649856\\n\", \"4092192268041\\n\", \"7\\n\", \"4\\n\", \"268\\n\", \"4\\n\", \"50\\n\", \"506507264\\n\", \"443973777333804\\n\", \"500\\n\", \"-1\\n\", \"11681102568\\n\", \"730\\n\", \"19071909388928\\n\", \"373939172\\n\", \"18864910278060\\n\", \"10424043522\\n\", \"7542072002\\n\", \"185\\n\", \"-1\\n\", \"979283524\\n\", \"8099000000000\\n\", \"-1\\n\", \"3784808102\\n\", \"285845006\\n\", \"3\\n\", \"30\\n\", \"63\\n\", \"181457955\\n\", \"999283748\\n\", \"500000000000000000\\n\", \"3\\n\", \"249999999750000000\\n\", \"1000000000\\n\", \"6172\\n\", \"990000000\\n\", \"56463217396\\n\", \"2975898412\\n\", \"500004999499995000\\n\", \"668140036\\n\", \"5505276296\\n\", \"2642837704515\\n\", \"47435966014\\n\", \"28401873\\n\", \"100\\n\", \"1000000000\\n\", \"-1\\n\", \"3\\n\", \"13748\\n\", \"9\\n\", \"1\\n\", \"10133660040\\n\", \"7\\n\", \"173605536\\n\", \"296333168238666852\\n\", \"158398860\\n\", \"1262530802\\n\", \"28\\n\", \"5\\n\", \"1799999982\\n\", \"55434271\\n\", \"22\\n\", \"88208737\\n\", \"5407977834\\n\", \"2\\n\", \"674492650\\n\", \"4\\n\", \"19999995780\\n\", \"798571511\\n\", \"3867033054\\n\", \"6623269354608\\n\", \"6\\n\", \"7275365504\\n\", \"1013419136918948\\n\", \"1000000\\n\", \"7416464120\\n\", \"589\\n\", \"560908758\\n\", \"-1\\n\", \"1\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"1\\n\", \"5\\n\", \"1\\n\", \"-1\\n\", \"-1\\n\", \"1\\n\", \"2\\n\", \"4\\n\", \"2\\n\", \"100\\n\", \"-1\\n\", \"8\\n\", \"-1\\n\", \"6\\n\"]}", "source": "taco"}
|
Jzzhu has a big rectangular chocolate bar that consists of n × m unit squares. He wants to cut this bar exactly k times. Each cut must meet the following requirements:
* each cut should be straight (horizontal or vertical);
* each cut should go along edges of unit squares (it is prohibited to divide any unit chocolate square with cut);
* each cut should go inside the whole chocolate bar, and all cuts must be distinct.
The picture below shows a possible way to cut a 5 × 6 chocolate for 5 times.
<image>
Imagine Jzzhu have made k cuts and the big chocolate is splitted into several pieces. Consider the smallest (by area) piece of the chocolate, Jzzhu wants this piece to be as large as possible. What is the maximum possible area of smallest piece he can get with exactly k cuts? The area of a chocolate piece is the number of unit squares in it.
Input
A single line contains three integers n, m, k (1 ≤ n, m ≤ 109; 1 ≤ k ≤ 2·109).
Output
Output a single integer representing the answer. If it is impossible to cut the big chocolate k times, print -1.
Examples
Input
3 4 1
Output
6
Input
6 4 2
Output
8
Input
2 3 4
Output
-1
Note
In the first sample, Jzzhu can cut the chocolate following the picture below:
<image>
In the second sample the optimal division looks like this:
<image>
In the third sample, it's impossible to cut a 2 × 3 chocolate 4 times.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n0 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 0 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n1 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 6 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n0 -1 0 -1\\n4\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 9 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 2 5 2 -1 5\\n\", \"7\\n5\\n-1 18 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 2 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n0 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 0 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 1 -1 5\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 0 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 2 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n0 -1 0 -1\\n4\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 20 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 5 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 14 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n-1 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 0 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 3 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 0 -1 0\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 0 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 0 5\\n\", \"7\\n5\\n-1 10 -1 20 -1\\n5\\n-1 22 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 5 2 -1 0\\n\", \"7\\n5\\n-1 10 0 12 -1\\n5\\n-1 46 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 3 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 1 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 0 -1 0\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 0 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 10 2 0 5\\n\", \"7\\n5\\n-1 10 -1 20 -1\\n5\\n-1 22 28 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 5 2 -1 0\\n\", \"7\\n5\\n-1 10 0 14 -1\\n5\\n-1 46 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 3 2 -1 5\\n\", \"7\\n5\\n0 16 -1 12 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 1 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 0 -1 0\\n\", \"7\\n5\\n-1 16 -1 20 -1\\n5\\n-1 22 28 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 5 2 -1 0\\n\", \"7\\n5\\n-1 10 0 14 -1\\n5\\n-1 46 35 -1 35\\n6\\n-1 -1 9 -1 2 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 3 2 -1 5\\n\", \"7\\n5\\n-1 10 0 14 -1\\n5\\n-1 46 35 -1 35\\n6\\n-1 -1 9 -1 2 -1\\n2\\n-1 -1\\n2\\n1 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 3 2 -1 5\\n\", \"7\\n5\\n-1 10 0 14 -1\\n5\\n-1 46 35 0 35\\n6\\n-1 -1 9 -1 2 -1\\n2\\n-1 -1\\n2\\n1 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 3 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 0 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 0 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n1 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n0 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n0 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n1 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 0 6 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 3 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n0 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 0 3 -1\\n7\\n1 -1 7 9 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 0 9 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 82 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 9 2 -1 1\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n0 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 0 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 8 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 1 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n0 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n0 -1 3 -1\\n4\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 20 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 0 3 -1\\n7\\n0 -1 7 5 2 -1 0\\n\", \"7\\n5\\n-1 10 -1 20 -1\\n5\\n-1 22 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 12 5 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 0 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 10 0 0 5\\n\", \"7\\n5\\n0 16 -1 12 -1\\n5\\n-1 40 20 -1 5\\n6\\n-1 -1 1 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 0 -1 0\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n0 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n1 -1\\n4\\n1 -1 4 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 0 6 0\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 70\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 3 5 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 1 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 0 9 2 -1 5\\n\", \"7\\n5\\n-1 17 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 0 3 -1\\n7\\n1 -1 2 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 82 24 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 9 2 -1 1\\n\", \"7\\n5\\n-1 1 -1 12 -1\\n5\\n0 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 0 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 6 -1\\n7\\n0 -1 7 8 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n0 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n0 -1 3 -1\\n4\\n1 -1 12 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 20 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 0 3 -1\\n7\\n0 -1 7 2 2 -1 0\\n\", \"7\\n5\\n-1 10 0 13 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 3 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 15 -1\\n5\\n-1 22 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 12 5 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 1 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n2 -1 3 -1\\n7\\n1 -1 7 6 0 -1 0\\n\", \"7\\n5\\n-1 3 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 0 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 10 0 0 5\\n\", \"7\\n5\\n0 16 -1 12 -1\\n5\\n-1 40 22 -1 5\\n6\\n-1 -1 1 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 0 -1 0\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n0 40 35 -1 52\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n1 -1\\n4\\n1 -1 4 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 70\\n6\\n-1 0 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 40 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 3 5 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 82 24 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n1 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 9 2 -1 1\\n\", \"7\\n5\\n-1 1 -1 12 -1\\n5\\n0 40 22 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 0 5\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 6 -1\\n7\\n0 -1 8 8 2 -1 0\\n\", \"7\\n5\\n-1 10 -1 20 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 1 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 0 3 -1\\n7\\n0 -1 7 2 2 -1 0\\n\", \"7\\n5\\n-1 10 0 13 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 3 3 2 -1 5\\n\", \"7\\n5\\n1 16 -1 12 -1\\n5\\n-1 40 22 -1 5\\n6\\n-1 -1 1 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 0 -1 0\\n\", \"7\\n5\\n-1 6 -1 24 -1\\n5\\n-1 40 20 -1 70\\n6\\n-1 0 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 0 13 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 3 3 0 -1 5\\n\", \"7\\n5\\n-1 3 -1 24 -1\\n5\\n-1 40 14 -1 35\\n6\\n-1 -1 6 -1 0 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 10 0 0 10\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 82 24 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n1 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 10 2 -1 1\\n\", \"7\\n5\\n-1 6 -1 24 -1\\n5\\n-1 60 20 -1 70\\n6\\n-1 0 6 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n0 -1 3 -1\\n4\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 9 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 9 2 -1 1\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 7 5 2 -1 0\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n-1 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n0 -1 3 -1\\n4\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 70 20 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 9 2 -2 5\\n\", \"7\\n5\\n-1 16 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 3 5 2 -1 5\\n\", \"7\\n5\\n-1 17 -1 24 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 6 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 2 5 2 -1 5\\n\", \"7\\n5\\n-1 10 0 12 -1\\n5\\n-1 40 35 -1 37\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 0 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n0 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 3 2 -1 5\\n\", \"7\\n5\\n-1 16 -1 12 -1\\n5\\n-1 40 20 -1 35\\n6\\n-1 -1 1 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n2 -1 3 -1\\n7\\n1 -1 7 5 0 -1 0\\n\", \"7\\n5\\n-1 10 0 14 -1\\n5\\n-1 46 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 0\\n7\\n1 -1 7 3 3 -1 5\\n\", \"7\\n5\\n-1 10 0 14 -1\\n5\\n-1 46 35 -1 35\\n6\\n-1 -1 9 -1 2 -1\\n2\\n-1 -1\\n2\\n1 -1\\n4\\n1 -1 3 0\\n7\\n2 -1 7 3 2 -1 5\\n\", \"7\\n5\\n-1 10 0 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 4 -1\\n2\\n-1 -1\\n2\\n1 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\", \"7\\n5\\n-1 10 -1 15 -1\\n5\\n-1 22 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n0 -1 12 5 1 -1 0\\n\", \"7\\n5\\n-1 10 -1 12 -1\\n5\\n-1 40 35 -1 35\\n6\\n-1 -1 9 -1 3 -1\\n2\\n-1 -1\\n2\\n0 -1\\n4\\n1 -1 3 -1\\n7\\n1 -1 7 5 2 -1 5\\n\"], \"outputs\": [\"1 11\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"1 11\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"1 11\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"2 14\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"2 14\\n5 37\\n3 6\\n0 0\\n0 0\\n2 1\\n3 4\\n\", \"12 11\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"2 14\\n20 30\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"4 20\\n20 30\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"1 11\\n5 37\\n3 6\\n0 0\\n0 1\\n1 2\\n3 4\\n\", \"1 11\\n5 37\\n2 7\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"2 14\\n50 45\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"4 20\\n20 30\\n2 4\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"2 14\\n5 37\\n3 6\\n0 0\\n0 0\\n0 0\\n3 4\\n\", \"2 14\\n50 45\\n3 6\\n0 0\\n0 0\\n1 2\\n7 4\\n\", \"4 20\\n20 30\\n2 4\\n0 0\\n0 0\\n1 2\\n3 3\\n\", \"3 21\\n20 30\\n2 4\\n0 0\\n0 0\\n1 2\\n3 3\\n\", \"1 11\\n40 35\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"12 11\\n5 37\\n3 6\\n0 0\\n0 0\\n3 2\\n3 4\\n\", \"2 14\\n20 30\\n3 6\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"2 14\\n50 45\\n3 6\\n0 0\\n0 0\\n1 2\\n4 4\\n\", \"4 20\\n20 30\\n3 3\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"2 14\\n5 37\\n1 2\\n0 0\\n0 0\\n0 0\\n3 4\\n\", \"5 15\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"1 15\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"12 11\\n5 37\\n3 6\\n0 0\\n0 0\\n3 2\\n4 4\\n\", \"2 14\\n20 30\\n3 6\\n0 0\\n0 0\\n1 2\\n5 3\\n\", \"4 20\\n20 30\\n3 3\\n0 0\\n0 0\\n1 2\\n5 4\\n\", \"5 15\\n13 28\\n3 6\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"12 11\\n11 40\\n3 6\\n0 0\\n0 0\\n3 2\\n4 4\\n\", \"2 14\\n20 30\\n1 2\\n0 0\\n0 0\\n1 2\\n5 3\\n\", \"4 20\\n20 30\\n3 3\\n0 0\\n0 0\\n1 2\\n8 4\\n\", \"5 15\\n7 28\\n3 6\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"14 12\\n11 40\\n3 6\\n0 0\\n0 0\\n3 2\\n4 4\\n\", \"16 14\\n20 30\\n1 2\\n0 0\\n0 0\\n1 2\\n5 3\\n\", \"2 18\\n7 28\\n3 6\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"14 12\\n11 40\\n4 5\\n0 0\\n0 0\\n3 2\\n4 4\\n\", \"14 12\\n11 40\\n4 5\\n0 0\\n0 1\\n3 2\\n4 4\\n\", \"14 12\\n35 46\\n4 5\\n0 0\\n0 1\\n3 2\\n4 4\\n\", \"1 11\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n7 3\\n\", \"12 11\\n5 37\\n3 6\\n0 0\\n0 1\\n1 2\\n3 4\\n\", \"16 20\\n20 30\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"1 11\\n40 35\\n3 6\\n0 0\\n0 1\\n1 2\\n3 4\\n\", \"1 11\\n5 37\\n9 7\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"2 14\\n50 45\\n3 6\\n0 0\\n0 0\\n1 2\\n3 3\\n\", \"4 20\\n20 30\\n2 4\\n0 0\\n0 0\\n2 1\\n3 4\\n\", \"2 14\\n50 45\\n3 6\\n0 0\\n0 0\\n3 3\\n7 4\\n\", \"2 14\\n50 45\\n3 6\\n0 0\\n0 0\\n1 2\\n9 2\\n\", \"2 14\\n62 51\\n3 6\\n0 0\\n0 0\\n1 2\\n7 4\\n\", \"1 11\\n40 35\\n3 6\\n0 0\\n0 0\\n1 2\\n5 4\\n\", \"1 11\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n6 3\\n\", \"2 14\\n19 18\\n3 6\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"2 14\\n40 35\\n3 6\\n0 0\\n0 0\\n2 1\\n3 4\\n\", \"5 15\\n5 37\\n3 6\\n0 0\\n0 0\\n3 3\\n4 3\\n\", \"5 15\\n13 28\\n3 6\\n0 0\\n0 0\\n1 2\\n7 6\\n\", \"4 20\\n20 30\\n3 3\\n0 0\\n0 0\\n1 2\\n10 4\\n\", \"16 14\\n20 22\\n1 2\\n0 0\\n0 0\\n1 2\\n5 3\\n\", \"1 11\\n40 35\\n3 6\\n0 0\\n0 1\\n2 2\\n3 4\\n\", \"1 11\\n5 37\\n9 9\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"4 20\\n25 45\\n2 4\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"4 20\\n20 30\\n2 4\\n0 0\\n0 0\\n1 2\\n3 1\\n\", \"2 14\\n50 45\\n4 5\\n0 0\\n0 0\\n1 2\\n9 2\\n\", \"4 20\\n20 30\\n2 4\\n0 0\\n0 0\\n3 3\\n3 3\\n\", \"2 14\\n58 53\\n3 6\\n0 0\\n0 0\\n1 2\\n7 4\\n\", \"6 6\\n40 35\\n3 6\\n0 0\\n0 0\\n1 2\\n5 4\\n\", \"1 11\\n5 37\\n3 6\\n0 0\\n0 0\\n3 3\\n6 3\\n\", \"2 14\\n40 35\\n3 6\\n0 0\\n0 0\\n2 1\\n7 6\\n\", \"5 15\\n5 37\\n3 6\\n0 0\\n0 0\\n3 3\\n5 3\\n\", \"13 11\\n5 37\\n3 6\\n0 0\\n0 0\\n3 2\\n4 4\\n\", \"3 12\\n13 28\\n3 6\\n0 0\\n0 0\\n1 2\\n7 6\\n\", \"2 14\\n20 30\\n1 2\\n0 0\\n0 0\\n1 2\\n6 3\\n\", \"11 13\\n20 30\\n3 3\\n0 0\\n0 0\\n1 2\\n10 4\\n\", \"16 14\\n18 22\\n1 2\\n0 0\\n0 0\\n1 2\\n5 3\\n\", \"1 11\\n40 43\\n3 6\\n0 0\\n0 1\\n2 2\\n3 4\\n\", \"4 20\\n25 45\\n6 3\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"12 28\\n20 30\\n2 4\\n0 0\\n0 0\\n1 2\\n3 1\\n\", \"2 14\\n58 53\\n3 6\\n0 0\\n0 1\\n1 2\\n7 4\\n\", \"6 6\\n40 28\\n3 6\\n0 0\\n0 0\\n1 2\\n5 4\\n\", \"1 11\\n5 37\\n3 6\\n0 0\\n0 0\\n3 3\\n6 4\\n\", \"5 15\\n5 37\\n1 2\\n0 0\\n0 0\\n3 3\\n5 3\\n\", \"13 11\\n5 37\\n3 6\\n0 0\\n0 0\\n3 2\\n2 3\\n\", \"15 14\\n18 22\\n1 2\\n0 0\\n0 0\\n1 2\\n5 3\\n\", \"9 15\\n25 45\\n6 3\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"13 11\\n5 37\\n3 6\\n0 0\\n0 0\\n3 2\\n3 2\\n\", \"11 13\\n26 27\\n3 3\\n0 0\\n0 0\\n1 2\\n10 4\\n\", \"2 14\\n58 53\\n3 6\\n0 0\\n0 1\\n1 2\\n8 4\\n\", \"9 15\\n40 45\\n6 3\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"2 14\\n5 37\\n3 6\\n0 0\\n0 0\\n2 1\\n3 4\\n\", \"2 14\\n50 45\\n3 6\\n0 0\\n0 0\\n1 2\\n7 4\\n\", \"2 14\\n50 45\\n3 6\\n0 0\\n0 0\\n1 2\\n7 4\\n\", \"1 11\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n4 3\\n\", \"2 14\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\", \"2 14\\n5 37\\n3 6\\n0 0\\n0 0\\n2 1\\n3 4\\n\", \"2 14\\n50 45\\n3 6\\n0 0\\n0 0\\n1 2\\n7 4\\n\", \"4 20\\n20 30\\n2 4\\n0 0\\n0 0\\n1 2\\n3 3\\n\", \"4 20\\n20 30\\n2 4\\n0 0\\n0 0\\n1 2\\n3 3\\n\", \"12 11\\n5 37\\n3 6\\n0 0\\n0 0\\n3 2\\n3 4\\n\", \"12 11\\n5 37\\n3 6\\n0 0\\n0 0\\n3 2\\n4 4\\n\", \"2 14\\n20 30\\n1 2\\n0 0\\n0 0\\n1 2\\n5 3\\n\", \"14 12\\n11 40\\n3 6\\n0 0\\n0 0\\n3 2\\n4 4\\n\", \"14 12\\n11 40\\n4 5\\n0 0\\n0 1\\n3 2\\n4 4\\n\", \"12 11\\n5 37\\n3 6\\n0 0\\n0 1\\n1 2\\n3 4\\n\", \"3 12\\n13 28\\n3 6\\n0 0\\n0 0\\n1 2\\n7 6\\n\", \"1 11\\n5 37\\n3 6\\n0 0\\n0 0\\n1 2\\n3 4\\n\"]}", "source": "taco"}
|
Dark is going to attend Motarack's birthday. Dark decided that the gift he is going to give to Motarack is an array $a$ of $n$ non-negative integers.
Dark created that array $1000$ years ago, so some elements in that array disappeared. Dark knows that Motarack hates to see an array that has two adjacent elements with a high absolute difference between them. He doesn't have much time so he wants to choose an integer $k$ ($0 \leq k \leq 10^{9}$) and replaces all missing elements in the array $a$ with $k$.
Let $m$ be the maximum absolute difference between all adjacent elements (i.e. the maximum value of $|a_i - a_{i+1}|$ for all $1 \leq i \leq n - 1$) in the array $a$ after Dark replaces all missing elements with $k$.
Dark should choose an integer $k$ so that $m$ is minimized. Can you help him?
-----Input-----
The input consists of multiple test cases. The first line contains a single integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases. The description of the test cases follows.
The first line of each test case contains one integer $n$ ($2 \leq n \leq 10^{5}$) — the size of the array $a$.
The second line of each test case contains $n$ integers $a_1, a_2, \ldots, a_n$ ($-1 \leq a_i \leq 10 ^ {9}$). If $a_i = -1$, then the $i$-th integer is missing. It is guaranteed that at least one integer is missing in every test case.
It is guaranteed, that the sum of $n$ for all test cases does not exceed $4 \cdot 10 ^ {5}$.
-----Output-----
Print the answers for each test case in the following format:
You should print two integers, the minimum possible value of $m$ and an integer $k$ ($0 \leq k \leq 10^{9}$) that makes the maximum absolute difference between adjacent elements in the array $a$ equal to $m$.
Make sure that after replacing all the missing elements with $k$, the maximum absolute difference between adjacent elements becomes $m$.
If there is more than one possible $k$, you can print any of them.
-----Example-----
Input
7
5
-1 10 -1 12 -1
5
-1 40 35 -1 35
6
-1 -1 9 -1 3 -1
2
-1 -1
2
0 -1
4
1 -1 3 -1
7
1 -1 7 5 2 -1 5
Output
1 11
5 35
3 6
0 42
0 0
1 2
3 4
-----Note-----
In the first test case after replacing all missing elements with $11$ the array becomes $[11, 10, 11, 12, 11]$. The absolute difference between any adjacent elements is $1$. It is impossible to choose a value of $k$, such that the absolute difference between any adjacent element will be $\leq 0$. So, the answer is $1$.
In the third test case after replacing all missing elements with $6$ the array becomes $[6, 6, 9, 6, 3, 6]$. $|a_1 - a_2| = |6 - 6| = 0$; $|a_2 - a_3| = |6 - 9| = 3$; $|a_3 - a_4| = |9 - 6| = 3$; $|a_4 - a_5| = |6 - 3| = 3$; $|a_5 - a_6| = |3 - 6| = 3$.
So, the maximum difference between any adjacent elements is $3$.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"6 1\\n5 6 7 8 10 2\\n3 5 6 7 1 10\\n\", \"4 0\\n5 3 2 2\\n13 8 5 1\\n\", \"5 0\\n1 1 1 1 1\\n10 10 10 10 10\\n\", \"5 1\\n1 1 1 1 1\\n10 10 10 10 10\\n\", \"4 2\\n1 1 1 1\\n10 10 10 10\\n\", \"4 2\\n1 2 4 8\\n1 5 3 5\\n\", \"4 2\\n1 2 4 8\\n5 1 3 5\\n\", \"4 2\\n1 2 4 8\\n5 3 1 5\\n\", \"4 2\\n1 2 4 8\\n6 5 3 1\\n\", \"4 3\\n1 1 1 1\\n10 10 10 10\\n\", \"4 3\\n1 2 4 8\\n1 5 3 5\\n\", \"4 3\\n1 2 4 8\\n5 1 3 5\\n\", \"4 3\\n1 2 4 8\\n5 3 1 5\\n\", \"4 3\\n1 2 4 8\\n6 5 3 1\\n\", \"4 1\\n2 5 2 1\\n101 2 101 100\\n\", \"5 1\\n1 2 2 2 1\\n1 101 101 101 100\\n\", \"4 2\\n1 2 4 8\\n17 15 16 1\\n\", \"4 3\\n1 2 4 8\\n17 15 16 1\\n\", \"4 1\\n3 2 3 4\\n8 1 2 8\\n\", \"5 1\\n3 2 3 4 5\\n8 1 2 8 8\\n\", \"5 1\\n3 2 1 4 8\\n8 1 10 3 5\\n\", \"4 1\\n3 2 1 5\\n8 5 4 4\\n\", \"5 1\\n2 5 11 12 13\\n1 2 100 100 100\\n\", \"4 1\\n2 5 11 11\\n1 2 100 100\\n\", \"4 1\\n10 10 9 100\\n1 10 10 1000000\\n\", \"4 1\\n10 9 10 100\\n1 10 10 1000000\\n\", \"4 1\\n10 9 9 7\\n1 11 11 10\\n\", \"6 1\\n1 10 10 5 20 100\\n1000000 1 10 10 100 1000000\\n\", \"6 1\\n1 10 10 20 5 100\\n1000000 1 10 100 10 1000000\\n\", \"4 1\\n1 1 3 5\\n100 100 1 100\\n\", \"5 1\\n1 1 4 5 12\\n100 100 7 2 10\\n\", \"4 1\\n1 12 13 20\\n10 5 4 100\\n\", \"5 1\\n1 12 13 20 30\\n10 5 4 1 100\\n\", \"4 1\\n1 12 13 20\\n10 5 4 100\\n\", \"6 1\\n1 10 10 5 20 100\\n1000000 1 10 10 100 1000000\\n\", \"5 0\\n1 1 1 1 1\\n10 10 10 10 10\\n\", \"4 3\\n1 2 4 8\\n5 1 3 5\\n\", \"4 3\\n1 2 4 8\\n17 15 16 1\\n\", \"6 1\\n1 10 10 20 5 100\\n1000000 1 10 100 10 1000000\\n\", \"4 2\\n1 2 4 8\\n1 5 3 5\\n\", \"4 2\\n1 2 4 8\\n5 3 1 5\\n\", \"4 3\\n1 2 4 8\\n1 5 3 5\\n\", \"4 1\\n3 2 1 5\\n8 5 4 4\\n\", \"4 1\\n2 5 2 1\\n101 2 101 100\\n\", \"4 1\\n2 5 11 11\\n1 2 100 100\\n\", \"5 1\\n1 2 2 2 1\\n1 101 101 101 100\\n\", \"4 3\\n1 1 1 1\\n10 10 10 10\\n\", \"4 1\\n3 2 3 4\\n8 1 2 8\\n\", \"5 1\\n1 1 1 1 1\\n10 10 10 10 10\\n\", \"4 3\\n1 2 4 8\\n6 5 3 1\\n\", \"4 2\\n1 1 1 1\\n10 10 10 10\\n\", \"5 1\\n2 5 11 12 13\\n1 2 100 100 100\\n\", \"5 1\\n3 2 3 4 5\\n8 1 2 8 8\\n\", \"4 1\\n10 9 9 7\\n1 11 11 10\\n\", \"4 1\\n1 1 3 5\\n100 100 1 100\\n\", \"4 2\\n1 2 4 8\\n17 15 16 1\\n\", \"5 1\\n3 2 1 4 8\\n8 1 10 3 5\\n\", \"5 1\\n1 12 13 20 30\\n10 5 4 1 100\\n\", \"4 0\\n5 3 2 2\\n13 8 5 1\\n\", \"4 2\\n1 2 4 8\\n6 5 3 1\\n\", \"4 2\\n1 2 4 8\\n5 1 3 5\\n\", \"4 1\\n10 10 9 100\\n1 10 10 1000000\\n\", \"4 3\\n1 2 4 8\\n5 3 1 5\\n\", \"5 1\\n1 1 4 5 12\\n100 100 7 2 10\\n\", \"4 1\\n10 9 10 100\\n1 10 10 1000000\\n\", \"4 1\\n1 12 13 20\\n10 5 0 100\\n\", \"5 0\\n2 1 1 1 1\\n10 10 10 10 10\\n\", \"4 4\\n1 2 4 8\\n5 1 3 5\\n\", \"4 3\\n1 4 4 8\\n17 15 16 1\\n\", \"6 1\\n1 10 10 20 5 100\\n1000000 1 6 100 10 1000000\\n\", \"4 2\\n1 2 4 8\\n2 5 3 5\\n\", \"4 3\\n1 2 5 8\\n1 5 3 5\\n\", \"4 1\\n3 2 1 5\\n10 5 4 4\\n\", \"4 1\\n2 5 1 1\\n101 2 101 100\\n\", \"4 1\\n2 5 11 11\\n1 2 100 101\\n\", \"4 1\\n3 2 5 4\\n8 1 2 8\\n\", \"4 3\\n1 2 4 8\\n6 5 3 2\\n\", \"4 0\\n10 9 9 7\\n1 11 11 10\\n\", \"4 2\\n1 1 3 5\\n100 100 1 100\\n\", \"5 1\\n3 2 1 4 10\\n8 1 10 3 5\\n\", \"5 1\\n1 12 0 20 30\\n10 5 4 1 100\\n\", \"4 0\\n5 3 2 3\\n13 8 5 1\\n\", \"4 2\\n1 2 0 8\\n6 5 3 1\\n\", \"4 2\\n10 10 9 100\\n1 10 10 1000000\\n\", \"4 1\\n10 9 10 100\\n1 13 10 1000000\\n\", \"6 1\\n5 6 7 8 10 2\\n3 9 6 7 1 10\\n\", \"4 1\\n1 12 1 20\\n10 5 0 100\\n\", \"6 1\\n1 15 10 20 5 100\\n1000000 1 6 100 10 1000000\\n\", \"4 2\\n1 2 4 5\\n2 5 3 5\\n\", \"4 1\\n4 2 1 5\\n10 5 4 4\\n\", \"5 2\\n3 2 1 4 10\\n8 1 10 3 5\\n\", \"4 2\\n8 10 9 100\\n1 10 10 1000000\\n\", \"4 2\\n1 6 4 8\\n5 3 2 5\\n\", \"4 2\\n1 2 4 8\\n5 3 2 5\\n\", \"5 1\\n1 2 3 2 1\\n1 101 101 101 100\\n\", \"4 3\\n1 1 2 1\\n10 10 10 10\\n\", \"5 1\\n1 1 1 1 2\\n10 10 10 10 10\\n\", \"5 1\\n3 2 2 4 5\\n8 1 2 8 8\\n\", \"4 4\\n1 2 4 8\\n17 15 16 1\\n\", \"4 2\\n1 2 4 8\\n3 1 3 5\\n\", \"4 1\\n1 2 4 8\\n5 3 1 5\\n\", \"5 1\\n1 2 4 5 12\\n100 100 7 2 10\\n\", \"4 4\\n1 2 4 8\\n5 2 3 5\\n\", \"4 5\\n1 4 4 8\\n17 15 16 1\\n\", \"4 2\\n1 3 4 8\\n5 3 2 5\\n\", \"4 3\\n1 2 5 8\\n0 5 3 5\\n\", \"4 1\\n4 5 1 1\\n101 2 101 100\\n\", \"4 3\\n1 1 1 0\\n10 10 10 10\\n\", \"4 1\\n3 2 5 4\\n8 0 2 8\\n\", \"5 1\\n1 1 1 1 2\\n10 10 10 10 20\\n\", \"4 3\\n1 2 4 8\\n6 5 3 0\\n\", \"5 1\\n1 2 2 4 5\\n8 1 2 8 8\\n\", \"4 2\\n1 1 4 5\\n100 100 1 100\\n\", \"4 0\\n5 3 2 3\\n13 8 8 1\\n\", \"4 2\\n1 2 0 8\\n6 5 1 1\\n\", \"4 2\\n1 2 4 8\\n3 1 2 5\\n\", \"4 1\\n1 2 7 8\\n5 3 1 5\\n\", \"5 1\\n1 2 4 5 12\\n110 100 7 2 10\\n\", \"6 1\\n5 6 7 8 10 2\\n3 13 6 7 1 10\\n\", \"4 1\\n1 12 1 20\\n9 5 0 100\\n\", \"4 4\\n1 2 4 8\\n5 2 3 4\\n\", \"4 5\\n1 4 4 8\\n17 28 16 1\\n\", \"6 1\\n0 15 10 20 5 100\\n1000000 1 6 100 10 1000000\\n\", \"4 2\\n1 2 4 4\\n2 5 3 5\\n\", \"4 3\\n1 2 8 8\\n0 5 3 5\\n\", \"4 1\\n4 2 1 5\\n1 5 4 4\\n\", \"4 1\\n4 5 1 1\\n101 1 101 100\\n\", \"4 3\\n1 1 1 0\\n10 10 20 10\\n\", \"4 1\\n3 2 4 4\\n8 0 2 8\\n\", \"5 1\\n1 1 1 1 0\\n10 10 10 10 20\\n\", \"4 3\\n1 2 4 11\\n6 5 3 0\\n\", \"5 1\\n1 2 2 4 10\\n8 1 2 8 8\\n\", \"4 2\\n1 0 4 5\\n100 100 1 100\\n\", \"6 1\\n5 6 7 8 10 2\\n3 5 6 7 1 10\\n\"], \"outputs\": [\"35\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"14\\n\", \"14\\n\", \"14\\n\", \"12\\n\", \"0\\n\", \"14\\n\", \"14\\n\", \"14\\n\", \"12\\n\", \"7\\n\", \"6\\n\", \"7\\n\", \"7\\n\", \"9\\n\", \"14\\n\", \"14\\n\", \"3\\n\", \"40\\n\", \"26\\n\", \"119\\n\", \"119\\n\", \"27\\n\", \"144\\n\", \"144\\n\", \"7\\n\", \"15\\n\", \"40\\n\", \"71\\n\", \"40\\n\", \"144\\n\", \"0\\n\", \"14\\n\", \"7\\n\", \"144\\n\", \"14\\n\", \"14\\n\", \"14\\n\", \"3\\n\", \"7\\n\", \"26\\n\", \"6\\n\", \"0\\n\", \"9\\n\", \"0\\n\", \"12\\n\", \"0\\n\", \"40\\n\", \"14\\n\", \"27\\n\", \"7\\n\", \"7\\n\", \"14\\n\", \"71\\n\", \"1\\n\", \"12\\n\", \"14\\n\", \"119\\n\", \"14\\n\", \"15\\n\", \"119\\n\", \"41\\n\", \"0\\n\", \"14\\n\", \"7\\n\", \"144\\n\", \"13\\n\", \"15\\n\", \"3\\n\", \"6\\n\", \"26\\n\", \"11\\n\", \"12\\n\", \"34\\n\", \"9\\n\", \"16\\n\", \"58\\n\", \"2\\n\", \"8\\n\", \"128\\n\", \"119\\n\", \"35\\n\", \"29\\n\", \"149\\n\", \"10\\n\", \"4\\n\", \"19\\n\", \"126\\n\", \"17\\n\", \"13\\n\", \"7\\n\", \"0\\n\", \"0\\n\", \"13\\n\", \"7\\n\", \"14\\n\", \"11\\n\", \"15\\n\", \"13\\n\", \"7\\n\", \"14\\n\", \"16\\n\", \"8\\n\", \"0\\n\", \"12\\n\", \"0\\n\", \"12\\n\", \"12\\n\", \"10\\n\", \"2\\n\", \"10\\n\", \"14\\n\", \"14\\n\", \"15\\n\", \"35\\n\", \"29\\n\", \"13\\n\", \"7\\n\", \"149\\n\", \"9\\n\", \"19\\n\", \"10\\n\", \"9\\n\", \"0\\n\", \"11\\n\", \"0\\n\", \"15\\n\", \"17\\n\", \"9\\n\", \"35\\n\"]}", "source": "taco"}
|
Mr. Chanek is currently participating in a science fair that is popular in town. He finds an exciting puzzle in the fair and wants to solve it.
There are $N$ atoms numbered from $1$ to $N$. These atoms are especially quirky. Initially, each atom is in normal state. Each atom can be in an excited. Exciting atom $i$ requires $D_i$ energy. When atom $i$ is excited, it will give $A_i$ energy. You can excite any number of atoms (including zero).
These atoms also form a peculiar one-way bond. For each $i$, $(1 \le i < N)$, if atom $i$ is excited, atom $E_i$ will also be excited at no cost. Initially, $E_i$ = $i+1$. Note that atom $N$ cannot form a bond to any atom.
Mr. Chanek must change exactly $K$ bonds. Exactly $K$ times, Mr. Chanek chooses an atom $i$, $(1 \le i < N)$ and changes $E_i$ to a different value other than $i$ and the current $E_i$. Note that an atom's bond can remain unchanged or changed more than once. Help Mr. Chanek determine the maximum energy that he can achieve!
note: You must first change exactly $K$ bonds before you can start exciting atoms.
-----Input-----
The first line contains two integers $N$ $K$ $(4 \le N \le 10^5, 0 \le K < N)$, the number of atoms, and the number of bonds that must be changed.
The second line contains $N$ integers $A_i$ $(1 \le A_i \le 10^6)$, which denotes the energy given by atom $i$ when on excited state.
The third line contains $N$ integers $D_i$ $(1 \le D_i \le 10^6)$, which denotes the energy needed to excite atom $i$.
-----Output-----
A line with an integer that denotes the maximum number of energy that Mr. Chanek can get.
-----Example-----
Input
6 1
5 6 7 8 10 2
3 5 6 7 1 10
Output
35
-----Note-----
An optimal solution to change $E_5$ to 1 and then excite atom 5 with energy 1. It will cause atoms 1, 2, 3, 4, 5 be excited. The total energy gained by Mr. Chanek is (5 + 6 + 7 + 8 + 10) - 1 = 35.
Another possible way is to change $E_3$ to 1 and then exciting atom 3 (which will excite atom 1, 2, 3) and exciting atom 4 (which will excite atom 4, 5, 6). The total energy gained by Mr. Chanek is (5 + 6 + 7 + 8 + 10 + 2) - (6 + 7) = 25 which is not optimal.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 5\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 6 8\\n1 2 3 5 10 11\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 3 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 12 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 2 6\\n1 3 5 12 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 8 5\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 3\\n1 2 3 4 3 8\\n1 2 8 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 6 5 10 11\\n1 3 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 2 12 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 2\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 3 6\\n1 3 5 6 8 4\\n1 2 3 4 4 5\\n1 2 3 4 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 3 2 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 6 5 10 11\\n1 3 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 4 8 4\\n1 2 3 6 5 8\\n1 2 4 9 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 5 10\\n1 3 5 6 12 3\\n1 2 3 2 6 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 2 6\\n1 3 5 12 8 4\\n1 2 6 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 2 5 6\\n1 3 5 6 8 4\\n1 2 6 4 5 8\\n1 2 6 5 10 11\\n1 3 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 6 5 8\\n1 3 3 5 10 5\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 8 6\\n1 3 5 11 8 4\\n1 2 6 4 5 8\\n1 2 4 8 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 10\\n1 3 5 6 12 3\\n1 2 3 4 6 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 3 3 4 3 6\\n1 3 5 2 8 4\\n1 2 3 5 2 5\\n1 2 3 4 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 11\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 10\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 2 12 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 10 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 10\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 9 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 10 8 4\\n1 2 3 4 5 8\\n1 2 4 9 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 2 6\\n1 3 5 12 8 4\\n1 2 3 4 3 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 3\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 5\\n1 3 3 4 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 6 8\\n1 2 3 5 10 11\\n1 3 3 2 9 11\", \"5\\n1 2 3 4 8 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 4 8\\n1 2 3 5 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 8 12 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 3\\n1 2 3 4 3 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 9\\n1 3 3 4 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 11\\n1 3 3 5 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 10 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 10\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 4\\n1 2 4 5 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 4 8\\n1 2 3 5 10 11\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 3 2 11 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 3\\n1 2 3 4 5 8\\n1 2 4 5 12 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 4 10 5\\n1 3 3 4 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 4 8\\n1 2 3 4 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 8 12 4\\n1 2 4 4 5 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 3 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 9\\n1 3 3 4 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 3\\n1 4 3 4 5 8\\n1 2 4 5 12 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 4 5\\n1 2 3 4 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 8 12 4\\n1 2 4 4 5 8\\n1 2 4 5 10 11\\n1 4 3 6 9 5\", \"5\\n1 2 3 3 5 6\\n1 3 2 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 9\\n1 3 3 4 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 3\\n1 4 3 4 5 8\\n1 2 4 3 12 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 8 6\\n1 3 5 6 8 4\\n1 2 3 4 4 5\\n1 2 3 4 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 3 4 8 6\\n1 3 5 8 12 4\\n1 2 4 4 5 8\\n1 2 4 5 10 11\\n1 4 3 6 9 5\", \"5\\n1 2 3 4 8 6\\n1 3 5 8 12 4\\n1 2 4 3 5 8\\n1 2 4 5 10 11\\n1 4 3 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 9 8\\n1 2 3 5 10 5\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 5 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 10\", \"5\\n1 2 3 4 5 6\\n1 3 5 4 8 4\\n1 2 3 4 5 8\\n1 2 4 9 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 2 6\\n1 3 5 12 8 4\\n1 2 3 4 3 8\\n1 2 4 9 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 3\\n1 2 3 2 3 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 4 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 11\\n1 3 3 5 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 10 6 8 4\\n1 3 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 10\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 10 4\\n1 2 3 4 5 4\\n1 2 4 5 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 4 8\\n1 2 3 8 10 11\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 4 8\\n1 2 4 5 10 11\\n1 3 2 11 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 4 10 3\\n1 3 3 4 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 3\\n1 4 3 4 5 8\\n1 2 4 5 12 11\\n1 4 2 10 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 8 12 4\\n1 2 4 4 9 8\\n1 2 4 5 10 11\\n1 4 3 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 5 4 8\\n1 2 4 5 10 11\\n1 2 3 6 9 10\", \"5\\n1 2 3 4 2 6\\n1 3 5 12 8 4\\n1 2 4 4 3 8\\n1 2 4 9 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 3\\n1 2 3 2 6 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 2 4 5 6\\n1 3 5 6 10 4\\n1 2 3 4 5 4\\n1 2 4 5 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 2 6 8 4\\n1 2 3 4 4 8\\n1 2 4 5 10 11\\n1 3 2 11 9 5\", \"5\\n1 2 3 4 3 6\\n1 3 5 6 8 4\\n1 2 3 4 2 5\\n1 2 3 4 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 3 4 2 6\\n1 3 5 12 8 4\\n1 2 4 4 3 4\\n1 2 4 9 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 2 12 3\\n1 2 3 2 6 8\\n1 2 4 5 10 11\\n1 4 2 6 9 5\", \"5\\n1 2 2 4 2 6\\n1 3 5 6 10 4\\n1 2 3 4 5 4\\n1 2 4 5 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 3 6\\n1 3 5 6 8 4\\n1 2 3 4 2 5\\n1 3 3 4 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 2 4 2 4\\n1 3 5 6 10 4\\n1 2 3 4 5 4\\n1 2 4 5 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 4 3 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 4\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 3 3 5 10 5\\n1 3 3 6 9 11\", \"5\\n1 2 3 4 5 10\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 2 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 5\\n1 3 3 8 9 11\", \"5\\n1 2 3 3 2 6\\n1 3 5 12 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 12 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 4 2 6 13 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 10 8 4\\n1 2 3 4 5 8\\n1 2 4 9 6 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 2 6\\n1 3 5 12 8 4\\n1 2 3 4 3 8\\n1 2 4 5 10 11\\n1 2 3 6 11 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 5\\n1 5 3 4 9 11\", \"5\\n1 2 3 4 8 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 8 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 6 10 9\\n1 3 3 4 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 3 5 10 11\\n1 3 3 5 3 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 12 8 4\\n1 2 3 4 5 4\\n1 2 4 5 10 11\\n1 3 2 6 9 11\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 4 8\\n1 2 3 5 10 3\\n1 3 3 6 9 11\", \"5\\n1 4 3 4 8 5\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 2\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 3 3\\n1 4 3 4 5 8\\n1 2 4 5 12 11\\n1 4 2 6 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 8 12 4\\n1 2 4 4 5 8\\n1 2 4 5 10 11\\n1 4 2 12 9 5\", \"5\\n1 2 3 4 5 6\\n1 3 5 6 8 4\\n1 2 3 4 5 8\\n1 2 4 5 10 11\\n1 2 3 6 9 11\"], \"outputs\": [\"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nyes\\nyes\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nyes\\n\", \"yes\\nno\\nno\\nyes\\nno\\n\", \"no\\nno\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"no\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nno\\nyes\\n\", \"yes\\nyes\\nno\\nno\\nyes\\n\", \"yes\\nno\\nno\\nno\\nno\\n\", \"no\\nyes\\nno\\nno\\nno\\n\", \"no\\nyes\\nno\\nno\\nyes\\n\", \"yes\\nno\\nyes\\nyes\\nno\\n\", \"no\\nno\\nno\\nyes\\nyes\\n\", \"no\\nno\\nyes\\nyes\\nno\\n\", \"no\\nyes\\nyes\\nno\\nyes\\n\", \"yes\\nyes\\nyes\\nno\\nno\\n\", \"yes\\nno\\nyes\\nno\\nno\\n\", \"no\\nno\\nyes\\nyes\\nyes\\n\", \"no\\nno\\nno\\nno\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nyes\\n\", \"yes\\nno\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nno\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nno\\n\", \"no\\nno\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nyes\\nyes\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"no\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"no\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nno\\nyes\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nno\\n\", \"no\\nno\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"no\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"no\\nno\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"no\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"no\\nyes\\nno\\nno\\nno\\n\", \"no\\nno\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"no\\nyes\\nno\\nyes\\nno\\n\", \"no\\nyes\\nno\\nno\\nno\\n\", \"no\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"no\\nyes\\nno\\nyes\\nno\\n\", \"no\\nyes\\nno\\nno\\nno\\n\", \"no\\nno\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nno\\nno\\n\", \"no\\nno\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nno\\nno\\n\", \"no\\nyes\\nno\\nyes\\nno\\n\", \"yes\\nno\\nno\\nyes\\nyes\\n\", \"yes\\nno\\nno\\nyes\\nno\\n\", \"yes\\nyes\\nno\\nyes\\nno\"]}", "source": "taco"}
|
There is "7 rows" in the game using playing cards. Here we consider a game that simplifies it. Arrange 7 using 13 cards with numbers 1 to 13 written on each. In the match, the game progresses as follows with only two players.
1. Place 7 cards in the "field".
2. Six remaining cards will be randomly distributed to the two parties.
3. Of the cards on the play, if there is a card with a number consecutive to the number of the card in the field, put one of them in the field. Players must place cards whenever they can. Only when there is no card, it is the opponent's turn without issuing a card.
4. Place your card in the field in the same way as you do.
5. Repeat steps 3 and 4 until you run out of cards on one side. The winner is the one who puts all the cards in hand first.
When given the number of the first card, create a program that determines and outputs at least one procedure for the first player to win, no matter how the second player takes out the card.
Input
The input is given in the following format.
N
game1
game2
::
gameN
The first line gives the number of times the game is played N (1 ≤ N ≤ 100). The following N lines are given the information gamei for the i-th game. Each gamei is given in the following format.
f1 f2 f3 f4 f5 f6
fj (1 ≤ fj ≤ 13, fj ≠ 7) is the number of the card to be dealt first. However, duplicate numbers do not appear on the same line (fj ≠ fk for j ≠ k).
Output
For each game, no matter how the second player puts out the card, if there is at least one procedure for the first player to win, "yes" is output, otherwise "no" is output on one line.
Example
Input
5
1 2 3 4 5 6
1 3 5 6 8 4
1 2 3 4 5 8
1 2 4 5 10 11
1 2 3 6 9 11
Output
yes
yes
no
yes
no
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\\n12 3 45\\n\", \"2\\n123 456\\n\", \"20\\n80 9 55 1 98 29 81 10 96 100 70 87 86 12 58 82 10 22 59 13\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 1756 5265 247 5494 3509 6089 2931 7372 4939 8030 2901 1150 5389 7168 6213 2723 4301 7250 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9533 8555 6372 1517 8034 6547 1148 9651 2399 3065 9675 3418 7758 3226 9844 4234 510 7652 162 8010 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 6999 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"20\\n4 53 9 79 47 2 64 98 51 82 14 30 77 41 69 4 37 85 81 62\\n\", \"1\\n123767132\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 1651 39 4268 8290 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 5004 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 5327 6763 2063 6708 4733 8339 2933 8477 7857 6074 1299 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"20\\n28 98 66 48 1 74 39 86 11 68 57 82 71 78 96 21 51 35 3 11\\n\", \"20\\n56 42 16 26 62 47 23 74 70 47 97 26 65 12 15 38 78 97 21 52\\n\", \"20\\n76 86 70 7 16 24 10 62 26 29 40 65 55 49 34 55 92 47 43 100\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 521 1898 8004 5009 6146 7735 8024 4006 4845 9123 2957 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 5815 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 1928 5663 9273 7408 2851 5713 8355 1106 812 5732 6398 3099 2579\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 9287 3059 8964 785 2614 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 577 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 9208 3144 2850 6044 3842 232 256 653 90 3959 1606 550 9846 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n15 7214 8212 3205 5610 4217 5220 235 5691 7149 2027 7344 6416 139 481 4653 4909 8693 9715 6209 2087 6580 1234 6189 7049 580 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 9635 3275 1958 9867 8912 9241 5518 1497 4943 1650 937 5895 8865 7544 6821 340\\n\", \"20\\n76 86 70 7 16 24 10 62 26 29 40 65 55 49 34 55 92 47 43 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 9287 3059 8964 785 2614 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 577 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 9208 3144 2850 6044 3842 232 256 653 90 3959 1606 550 9846 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 1651 39 4268 8290 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 5004 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 5327 6763 2063 6708 4733 8339 2933 8477 7857 6074 1299 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"100\\n15 7214 8212 3205 5610 4217 5220 235 5691 7149 2027 7344 6416 139 481 4653 4909 8693 9715 6209 2087 6580 1234 6189 7049 580 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 9635 3275 1958 9867 8912 9241 5518 1497 4943 1650 937 5895 8865 7544 6821 340\\n\", \"20\\n28 98 66 48 1 74 39 86 11 68 57 82 71 78 96 21 51 35 3 11\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 1756 5265 247 5494 3509 6089 2931 7372 4939 8030 2901 1150 5389 7168 6213 2723 4301 7250 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9533 8555 6372 1517 8034 6547 1148 9651 2399 3065 9675 3418 7758 3226 9844 4234 510 7652 162 8010 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 6999 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"1\\n123767132\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 521 1898 8004 5009 6146 7735 8024 4006 4845 9123 2957 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 5815 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 1928 5663 9273 7408 2851 5713 8355 1106 812 5732 6398 3099 2579\\n\", \"20\\n80 9 55 1 98 29 81 10 96 100 70 87 86 12 58 82 10 22 59 13\\n\", \"20\\n56 42 16 26 62 47 23 74 70 47 97 26 65 12 15 38 78 97 21 52\\n\", \"20\\n4 53 9 79 47 2 64 98 51 82 14 30 77 41 69 4 37 85 81 62\\n\", \"20\\n76 86 70 7 16 24 10 62 26 29 40 65 87 49 34 55 92 47 43 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 960 3059 8964 785 2614 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 577 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 9208 3144 2850 6044 3842 232 256 653 90 3959 1606 550 9846 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 1651 39 4268 8290 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 5004 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 1303 6763 2063 6708 4733 8339 2933 8477 7857 6074 1299 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"100\\n15 7214 8212 3205 5610 4217 5220 235 5691 7149 2027 7344 6416 139 481 4653 4909 8693 9715 6209 2087 6580 1234 6189 7049 580 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 9635 3275 2556 9867 8912 9241 5518 1497 4943 1650 937 5895 8865 7544 6821 340\\n\", \"20\\n28 98 66 48 2 74 39 86 11 68 57 82 71 78 96 21 51 35 3 11\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 1756 5265 247 5494 3509 6089 2931 2429 4939 8030 2901 1150 5389 7168 6213 2723 4301 7250 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9533 8555 6372 1517 8034 6547 1148 9651 2399 3065 9675 3418 7758 3226 9844 4234 510 7652 162 8010 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 6999 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"1\\n21106256\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 521 1898 8004 5009 6146 13634 8024 4006 4845 9123 2957 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 5815 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 1928 5663 9273 7408 2851 5713 8355 1106 812 5732 6398 3099 2579\\n\", \"20\\n80 9 38 1 98 29 81 10 96 100 70 87 86 12 58 82 10 22 59 13\\n\", \"20\\n56 42 16 26 62 47 23 74 70 47 97 26 65 12 15 53 78 97 21 52\\n\", \"20\\n4 53 9 79 47 2 64 98 51 82 14 30 77 41 69 4 37 85 50 62\\n\", \"3\\n12 2 45\\n\", \"2\\n64 456\\n\", \"20\\n76 86 70 7 16 24 10 62 26 29 40 65 87 73 34 55 92 47 43 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 960 3059 8964 785 2614 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 577 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 9208 3144 2850 6044 3842 232 256 255 90 3959 1606 550 9846 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 3026 39 4268 8290 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 5004 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 1303 6763 2063 6708 4733 8339 2933 8477 7857 6074 1299 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"100\\n15 7214 8212 3205 5610 4217 5220 235 5691 7149 2027 7344 6416 139 481 4653 4909 8693 9715 6209 2087 6580 1234 6189 7049 580 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 15969 3275 2556 9867 8912 9241 5518 1497 4943 1650 937 5895 8865 7544 6821 340\\n\", \"20\\n28 98 66 48 2 74 39 86 20 68 57 82 71 78 96 21 51 35 3 11\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 1756 5265 247 5494 3509 6089 2931 2429 4939 8030 2901 1150 5389 7168 6213 2723 4301 7250 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9533 8555 6372 1517 8034 6547 1148 9651 2399 3065 9675 3418 7758 3226 9844 4234 510 7652 162 8010 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 3368 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"1\\n27524816\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 521 1898 8004 5009 6146 13634 8024 4006 4845 9123 5247 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 5815 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 1928 5663 9273 7408 2851 5713 8355 1106 812 5732 6398 3099 2579\\n\", \"20\\n80 9 38 1 98 29 81 10 96 100 70 87 86 12 58 82 10 22 59 17\\n\", \"20\\n56 42 16 26 62 47 23 74 70 47 97 26 65 12 15 93 78 97 21 52\\n\", \"20\\n4 53 9 79 47 2 64 98 51 34 14 30 77 41 69 4 37 85 50 62\\n\", \"3\\n12 2 81\\n\", \"2\\n64 316\\n\", \"20\\n76 86 70 7 16 24 10 75 26 29 40 65 87 73 34 55 92 47 43 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 960 3059 8964 785 2614 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 639 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 9208 3144 2850 6044 3842 232 256 255 90 3959 1606 550 9846 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 3026 39 4268 8290 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 5004 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 1303 6763 2063 6708 4733 8339 2933 8477 7857 6074 1165 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"100\\n15 7214 8212 3205 5610 4217 5220 235 5691 7149 2027 7344 6416 139 481 4653 4909 8693 9715 6209 2087 6580 1234 6189 7049 580 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 15969 3275 2556 9867 8912 9241 5518 1497 4943 1650 937 2820 8865 7544 6821 340\\n\", \"20\\n28 98 66 48 2 74 39 94 20 68 57 82 71 78 96 21 51 35 3 11\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 1756 5265 247 5494 3509 6089 2931 2429 4939 8030 2901 1150 5389 7168 6213 2723 4301 7250 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9533 8555 6372 1517 8034 6547 1148 9651 2399 3065 9675 3418 7758 3226 9844 4234 510 7652 162 4745 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 3368 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"1\\n52552165\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 521 1898 8004 5009 6146 13634 8024 4006 4845 9123 5247 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 5815 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 1928 5663 7672 7408 2851 5713 8355 1106 812 5732 6398 3099 2579\\n\", \"20\\n93 42 16 26 62 47 23 74 70 47 97 26 65 12 15 93 78 97 21 52\\n\", \"20\\n4 53 11 79 47 2 64 98 51 34 14 30 77 41 69 4 37 85 50 62\\n\", \"3\\n11 2 81\\n\", \"2\\n72 316\\n\", \"20\\n76 86 70 7 16 24 10 75 26 29 40 65 87 73 34 55 92 47 8 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 960 3059 8964 785 2614 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 639 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 9208 3144 2850 6044 3842 232 256 255 90 3959 690 550 9846 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 3026 39 4268 8290 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 5004 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 1491 6763 2063 6708 4733 8339 2933 8477 7857 6074 1165 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"100\\n15 7214 8212 3205 5610 4217 5220 235 5691 7149 2027 7344 6416 139 481 4653 4909 8693 9715 6209 2087 6580 1234 6189 7049 580 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 15969 3275 2556 9867 8912 9241 5518 1497 4943 2451 937 2820 8865 7544 6821 340\\n\", \"20\\n28 98 66 48 2 74 39 94 20 52 57 82 71 78 96 21 51 35 3 11\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 1756 5265 247 5494 3509 6089 2931 2429 4939 8030 2901 1150 5389 7168 6213 2723 4301 7250 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9652 8555 6372 1517 8034 6547 1148 9651 2399 3065 9675 3418 7758 3226 9844 4234 510 7652 162 4745 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 3368 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"1\\n75807138\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 301 1898 8004 5009 6146 13634 8024 4006 4845 9123 5247 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 5815 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 1928 5663 7672 7408 2851 5713 8355 1106 812 5732 6398 3099 2579\\n\", \"20\\n93 42 16 26 62 47 23 74 70 47 97 26 65 12 15 93 78 10 21 52\\n\", \"20\\n4 53 11 79 47 2 64 98 51 34 14 30 77 41 113 4 37 85 50 62\\n\", \"3\\n11 1 81\\n\", \"2\\n95 316\\n\", \"20\\n76 86 70 7 16 24 10 75 26 29 40 65 87 73 34 55 92 47 6 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 960 3059 8964 785 1590 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 639 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 9208 3144 2850 6044 3842 232 256 255 90 3959 690 550 9846 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 3026 39 4268 8290 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 4774 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 1491 6763 2063 6708 4733 8339 2933 8477 7857 6074 1165 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"100\\n15 7214 8212 3205 5610 4217 2610 235 5691 7149 2027 7344 6416 139 481 4653 4909 8693 9715 6209 2087 6580 1234 6189 7049 580 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 15969 3275 2556 9867 8912 9241 5518 1497 4943 2451 937 2820 8865 7544 6821 340\\n\", \"20\\n28 98 66 48 2 74 39 94 20 52 57 82 2 78 96 21 51 35 3 11\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 1756 5265 247 5494 3509 6089 2931 2429 4939 8030 2901 1150 5389 7168 6213 2723 4301 7250 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9652 8555 6372 1517 8034 6547 1148 9651 2399 3065 9675 1149 7758 3226 9844 4234 510 7652 162 4745 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 3368 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"1\\n11795568\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 301 1898 8004 5009 6146 13634 8024 4006 4845 9123 5247 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 2674 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 1928 5663 7672 7408 2851 5713 8355 1106 812 5732 6398 3099 2579\\n\", \"20\\n93 42 16 26 62 47 23 74 70 47 97 26 7 12 15 93 78 10 21 52\\n\", \"20\\n4 53 11 38 47 2 64 98 51 34 14 30 77 41 113 4 37 85 50 62\\n\", \"3\\n8 1 81\\n\", \"2\\n116 316\\n\", \"20\\n76 86 70 7 16 24 10 75 26 29 32 65 87 73 34 55 92 47 6 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 960 3059 8964 785 1590 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 639 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 15661 3144 2850 6044 3842 232 256 255 90 3959 690 550 9846 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 3026 39 4268 8148 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 4774 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 1491 6763 2063 6708 4733 8339 2933 8477 7857 6074 1165 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"100\\n15 7214 8212 3205 5610 4217 2610 235 5691 7149 2027 7344 6416 139 481 4653 4909 8693 9715 6209 2087 6580 1234 6189 7049 519 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 15969 3275 2556 9867 8912 9241 5518 1497 4943 2451 937 2820 8865 7544 6821 340\\n\", \"20\\n28 98 66 48 2 74 18 94 20 52 57 82 2 78 96 21 51 35 3 11\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 1756 5265 247 5494 3509 6089 2931 2429 4939 8030 2901 1150 5389 7168 6213 2723 4301 8638 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9652 8555 6372 1517 8034 6547 1148 9651 2399 3065 9675 1149 7758 3226 9844 4234 510 7652 162 4745 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 3368 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"1\\n793339\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 301 1898 8004 5009 6146 13634 8024 4006 4845 9123 5247 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 2674 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 1928 5663 7672 7408 2851 5713 8355 1106 812 6406 6398 3099 2579\\n\", \"20\\n93 31 16 26 62 47 23 74 70 47 97 26 7 12 15 93 78 10 21 52\\n\", \"20\\n4 53 11 38 47 2 64 98 51 34 14 30 77 41 113 6 37 85 50 62\\n\", \"3\\n8 1 70\\n\", \"2\\n116 347\\n\", \"20\\n76 86 70 7 16 24 10 75 26 29 12 65 87 73 34 55 92 47 6 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 960 3059 8964 785 1590 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 639 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 15661 3144 2850 6044 3842 232 256 255 90 3959 690 550 16661 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 3026 39 4268 8148 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 4774 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 1491 6763 2063 3101 4733 8339 2933 8477 7857 6074 1165 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"100\\n15 7214 8212 5959 5610 4217 2610 235 5691 7149 2027 7344 6416 139 481 4653 4909 8693 9715 6209 2087 6580 1234 6189 7049 519 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 15969 3275 2556 9867 8912 9241 5518 1497 4943 2451 937 2820 8865 7544 6821 340\\n\", \"20\\n28 98 66 48 2 74 18 94 20 52 57 82 1 78 96 21 51 35 3 11\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 73 5265 247 5494 3509 6089 2931 2429 4939 8030 2901 1150 5389 7168 6213 2723 4301 8638 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9652 8555 6372 1517 8034 6547 1148 9651 2399 3065 9675 1149 7758 3226 9844 4234 510 7652 162 4745 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 3368 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"1\\n10190\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 301 1898 8004 5009 6146 13634 8024 4006 4845 9123 5247 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 2674 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 2989 5663 7672 7408 2851 5713 8355 1106 812 6406 6398 3099 2579\\n\", \"20\\n93 31 16 26 62 47 23 66 70 47 97 26 7 12 15 93 78 10 21 52\\n\", \"20\\n4 53 11 38 47 2 64 98 51 34 14 30 77 41 113 5 37 85 50 62\\n\", \"3\\n8 1 124\\n\", \"2\\n116 641\\n\", \"20\\n76 86 117 7 16 24 10 75 26 29 12 65 87 73 34 55 92 47 6 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 960 3059 8964 785 1590 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 639 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 15661 3144 2850 6044 3842 3 256 255 90 3959 690 550 16661 1567 8750 2804 7411 9986 7221 1163 9615 1284 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 3026 39 4268 8148 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 4774 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 1487 6763 2063 3101 4733 8339 2933 8477 7857 6074 1165 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 7311 9307 4840 2545 2041 5300\\n\", \"100\\n15 7214 8212 5959 5610 4217 2610 235 5691 7149 2027 7344 6416 139 481 4653 4909 13875 9715 6209 2087 6580 1234 6189 7049 519 8482 886 19 1763 5819 4630 9238 549 6236 7946 4585 5283 1187 2501 9159 4375 2374 7068 8223 8177 9645 8825 2547 5669 8725 6329 601 1131 9390 9293 8013 7198 5774 2460 3949 2190 3437 1264 2988 8366 5399 8021 1247 2342 3501 1149 9059 6354 9108 8686 9813 673 6804 7218 7400 8006 9002 3574 15969 3275 2556 9867 8912 9241 5518 1497 4943 2451 937 2820 8865 7544 6821 340\\n\", \"20\\n28 98 66 48 2 74 18 94 20 52 102 82 1 78 96 21 51 35 3 11\\n\", \"100\\n3615 1436 2205 5695 9684 7621 391 1579 557 420 73 5265 247 5494 3509 6089 2931 2429 4939 8030 2901 1150 5389 7168 6213 2723 4301 8638 3857 9178 4723 1932 1161 1412 8200 5226 1474 3495 9652 8555 6372 1517 8034 6547 1148 9651 2399 3065 1844 1149 7758 3226 9844 4234 510 7652 162 4745 8162 2732 2112 4041 3392 6344 671 4120 4659 7718 8660 7102 9098 6195 3368 9411 6710 2261 4388 7125 3808 978 398 9286 1280 7382 1095 8203 5687 9281 3722 8159 470 5735 4210 3694 2197 5422 816 7546 9965 2963\\n\", \"1\\n2877\\n\", \"100\\n7039 7577 5463 7876 8938 6398 2374 5567 301 1898 8004 3653 6146 13634 8024 4006 4845 9123 5247 2271 6649 7439 5602 1551 70 1443 8522 2111 8170 2152 3949 714 6557 7548 309 9826 3500 866 9474 1769 3961 6927 6519 1001 7849 8030 1914 7309 7589 6077 3576 4981 5642 8862 3406 4886 5945 4631 4017 536 2674 8850 2727 918 2702 6974 5148 3841 3259 2940 6750 8686 2718 1922 5586 3395 3549 6220 6653 782 9952 7446 2907 2206 7926 2579 4555 2989 5663 7672 7408 2851 5713 8355 1106 812 6406 6398 3099 2579\\n\", \"20\\n93 31 16 26 62 47 23 66 70 47 97 26 7 12 15 93 26 10 21 52\\n\", \"20\\n4 53 11 38 26 2 64 98 51 34 14 30 77 41 113 5 37 85 50 62\\n\", \"2\\n116 162\\n\", \"20\\n76 86 117 7 16 24 10 75 26 29 12 65 87 73 34 55 92 47 11 100\\n\", \"100\\n6591 1074 3466 3728 549 5440 533 3543 1536 2967 1587 304 6326 6410 8670 6736 4482 8431 1697 9264 8338 2995 3725 1805 488 4563 4261 6025 2602 1892 9297 4359 1139 7117 1423 4834 5663 7912 1245 960 3059 8964 785 1590 4226 7093 5537 7285 1929 4499 9803 7277 212 2311 9198 9355 6422 639 9919 4656 1734 85 4102 3986 956 7000 4910 1897 6648 15661 3144 2850 6044 3842 3 256 255 90 3959 690 550 16661 1567 8750 2804 7411 9986 7221 1163 9615 1882 7084 7631 1181 6220 505 9756 8692 7879 4916\\n\", \"100\\n463 6421 2912 1546 3999 5175 4357 2259 7380 6081 1148 7857 3532 4168 5643 8819 2568 6681 975 9216 4590 5217 6215 7422 6631 3026 39 4268 8148 2022 3175 8281 1552 980 9314 234 934 5133 6712 1880 2766 5042 4774 5455 6038 6010 6022 1553 4015 4544 3985 4033 223 7682 6302 2121 4832 3956 9872 8340 1487 6763 2063 3101 4733 8339 2933 8477 7857 6074 1165 5768 3029 7138 8653 9121 6901 6803 5306 9098 6803 2902 9941 3926 3269 5739 3823 7278 3413 5796 4346 9968 3024 3416 2252 9307 4840 2545 2041 5300\\n\", \"3\\n12 3 45\\n\", \"2\\n123 456\\n\"], \"outputs\": [\"12330\", \"1115598\", \"2248760\", \"674832474\", \"1675580\", \"116407724\", \"495837625\", \"1899280\", \"1934680\", \"2178920\", \"906817803\", \"167137718\", \"666837072\", \"2178920\\n\", \"167137718\\n\", \"495837625\\n\", \"666837072\\n\", \"1899280\\n\", \"674832474\\n\", \"116407724\\n\", \"906817803\\n\", \"2248760\\n\", \"1934680\\n\", \"1675580\\n\", \"2242660\\n\", \"13982254\\n\", \"347790637\\n\", \"613710519\\n\", \"1899500\\n\", \"671511939\\n\", \"820819272\\n\", \"117197055\\n\", \"2209020\\n\", \"1977580\\n\", \"1620160\\n\", \"12297\\n\", \"544420\\n\", \"2304640\\n\", \"968948807\\n\", \"355917431\\n\", \"423239624\\n\", \"1919480\\n\", \"596913898\\n\", \"853583545\\n\", \"97583996\\n\", \"2209900\\n\", \"2065580\\n\", \"1528600\\n\", \"21765\\n\", \"405620\\n\", \"2326400\\n\", \"979331007\\n\", \"344673031\\n\", \"451997183\\n\", \"1939240\\n\", \"663226810\\n\", \"231834051\\n\", \"103311602\\n\", \"2152920\\n\", \"1619940\\n\", \"21732\\n\", \"407776\\n\", \"2150400\\n\", \"474891819\\n\", \"356570831\\n\", \"420513930\\n\", \"1917720\\n\", \"674445710\\n\", \"611592828\\n\", \"81271602\\n\", \"1975380\\n\", \"1958120\\n\", \"21699\\n\", \"412242\\n\", \"2149960\\n\", \"519791772\\n\", \"396755184\\n\", \"493216989\\n\", \"1698240\\n\", \"636265516\\n\", \"281068233\\n\", \"3243561\\n\", \"1769120\\n\", \"1880700\\n\", \"12330\\n\", \"884664\\n\", \"2130200\\n\", \"618703130\\n\", \"385303984\\n\", \"492456889\\n\", \"1659420\\n\", \"682809963\\n\", \"304493706\\n\", \"987387961\\n\", \"1747800\\n\", \"1881140\\n\", \"10797\\n\", \"891286\\n\", \"2089800\\n\", \"400923629\\n\", \"208969343\\n\", \"549062583\\n\", \"1659200\\n\", \"990272781\\n\", \"101875547\\n\", \"8760355\\n\", \"1727140\\n\", \"1880920\\n\", \"117429\\n\", \"1551154\\n\", \"2604140\\n\", \"522469082\\n\", \"208865943\\n\", \"160575135\\n\", \"1997600\\n\", \"77872152\\n\", \"22887777\\n\", \"36852461\\n\", \"1621200\\n\", \"1842100\\n\", \"455576\\n\", \"2726740\\n\", \"586738882\\n\", \"13618808\\n\", \"12330\\n\", \"1115598\\n\"]}", "source": "taco"}
|
This problem differs from the previous one only in the absence of the constraint on the equal length of all numbers $a_1, a_2, \dots, a_n$.
A team of SIS students is going to make a trip on a submarine. Their target is an ancient treasure in a sunken ship lying on the bottom of the Great Rybinsk sea. Unfortunately, the students don't know the coordinates of the ship, so they asked Meshanya (who is a hereditary mage) to help them. He agreed to help them, but only if they solve his problem.
Let's denote a function that alternates digits of two numbers $f(a_1 a_2 \dots a_{p - 1} a_p, b_1 b_2 \dots b_{q - 1} b_q)$, where $a_1 \dots a_p$ and $b_1 \dots b_q$ are digits of two integers written in the decimal notation without leading zeros.
In other words, the function $f(x, y)$ alternately shuffles the digits of the numbers $x$ and $y$ by writing them from the lowest digits to the older ones, starting with the number $y$. The result of the function is also built from right to left (that is, from the lower digits to the older ones). If the digits of one of the arguments have ended, then the remaining digits of the other argument are written out. Familiarize with examples and formal definitions of the function below.
For example: $$f(1111, 2222) = 12121212$$ $$f(7777, 888) = 7787878$$ $$f(33, 44444) = 4443434$$ $$f(555, 6) = 5556$$ $$f(111, 2222) = 2121212$$
Formally, if $p \ge q$ then $f(a_1 \dots a_p, b_1 \dots b_q) = a_1 a_2 \dots a_{p - q + 1} b_1 a_{p - q + 2} b_2 \dots a_{p - 1} b_{q - 1} a_p b_q$; if $p < q$ then $f(a_1 \dots a_p, b_1 \dots b_q) = b_1 b_2 \dots b_{q - p} a_1 b_{q - p + 1} a_2 \dots a_{p - 1} b_{q - 1} a_p b_q$.
Mishanya gives you an array consisting of $n$ integers $a_i$, your task is to help students to calculate $\sum_{i = 1}^{n}\sum_{j = 1}^{n} f(a_i, a_j)$ modulo $998\,244\,353$.
-----Input-----
The first line of the input contains a single integer $n$ ($1 \le n \le 100\,000$) — the number of elements in the array. The second line of the input contains $n$ integers $a_1, a_2, \dots, a_n$ ($1 \le a_i \le 10^9$) — the elements of the array.
-----Output-----
Print the answer modulo $998\,244\,353$.
-----Examples-----
Input
3
12 3 45
Output
12330
Input
2
123 456
Output
1115598
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.625
|
{"tests": "{\"inputs\": [\"2 1\\n-1000000000 1000000000\\n2 1\\n2 1 2\\n\", \"4 4\\n2 -1000 100 3\\n2 1\\n3 2\\n4 1\\n2 1 3\\n2 2 2\\n1 1 -1000000000\\n2 1 4\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 4\\n2 3 3\\n\", \"6 3\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 4\\n2 3 3\\n\", \"2 1\\n-1000000000 1010000000\\n2 1\\n2 1 2\\n\", \"4 4\\n2 -1000 100 3\\n2 1\\n3 2\\n4 2\\n2 1 3\\n2 2 2\\n1 1 -1000000000\\n2 1 4\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 2 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 2\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 1 2\\n1 2 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 5 2\\n\", \"6 4\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 3 3\\n\", \"6 4\\n10 -9 2 -1 2 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 2 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n1 3 2\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 1 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 1 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 5 2\\n\", \"6 4\\n0 -9 4 -1 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -9 2 -1 2 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 2 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 4 -1 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 3 3\\n\", \"6 4\\n0 -9 4 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 3 3\\n\", \"6 4\\n0 -3 2 -1 2 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 2 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 4 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -3 2 -1 2 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 4 0 8 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -3 2 -1 2 -12\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 4 0 14 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -3 2 -1 2 -12\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 4\\n2 3 3\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 4\\n2 3 3\\n\", \"6 3\\n0 -9 2 0 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 4\\n2 2 3\\n\", \"4 4\\n2 -1000 100 3\\n2 1\\n3 2\\n4 2\\n2 2 3\\n2 2 2\\n1 1 -1000000000\\n2 1 4\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n4 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 5 2\\n\", \"6 3\\n0 -17 2 -1 4 -5\\n1 4\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 4\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n6 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n1 3 2\\n\", \"6 4\\n0 -9 0 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 6 3\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 2 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 1 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 0\\n2 1 2\\n2 5 2\\n\", \"6 4\\n0 -14 4 -1 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -2\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -3 2 -1 2 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 2 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 4 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -3 2 -1 2 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n0 -9 4 0 14 1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n10 -9 1 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n1 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n6 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 3 3\\n\", \"4 4\\n2 -1000 100 3\\n4 1\\n3 2\\n4 2\\n2 2 3\\n2 2 2\\n1 1 -1000000000\\n2 1 4\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n1 4\\n5 6\\n4 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 5 2\\n\", \"6 4\\n0 -9 2 -1 3 -6\\n1 5\\n6 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n1 3 2\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n4 6\\n6 2\\n6 3\\n1 2 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 1 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -1\\n2 1 2\\n2 5 2\\n\", \"6 3\\n0 0 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 4\\n1 2 3\\n\", \"6 4\\n0 -9 4 0 14 1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 2 3\\n\", \"6 4\\n0 -3 2 -1 2 0\\n1 5\\n1 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 4\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n1 4\\n5 6\\n4 2\\n6 3\\n2 1 4\\n1 2 -3\\n2 1 2\\n2 5 2\\n\", \"6 4\\n10 -9 2 -1 4 0\\n1 5\\n5 4\\n4 6\\n6 2\\n6 3\\n1 2 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -3 2 -1 2 0\\n1 5\\n1 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 5\\n2 3 3\\n\", \"6 4\\n0 -3 2 -1 2 0\\n1 5\\n1 4\\n5 6\\n6 2\\n6 3\\n2 2 3\\n1 1 -3\\n2 1 5\\n2 3 3\\n\", \"2 1\\n-1000000000 1000000010\\n2 1\\n2 1 2\\n\", \"6 4\\n0 -9 2 -1 4 -1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 4\\n2 4 3\\n\", \"2 1\\n-651044801 1010000000\\n2 1\\n2 1 2\\n\", \"6 4\\n-1 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 3 3\\n\", \"6 3\\n0 -17 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -6\\n2 1 4\\n2 3 3\\n\", \"6 4\\n10 -9 2 -1 2 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 3 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -2\\n2 1 2\\n1 3 2\\n\", \"6 4\\n0 -9 0 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -13 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 1 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 1 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 1\\n1 1 -3\\n2 1 2\\n2 5 2\\n\", \"6 4\\n10 -3 2 -1 2 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 2 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n-1 -9 4 0 8 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -9 4 0 0 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n10 -15 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 3\\n0 -9 2 0 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 4\\n2 2 3\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 4 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -14 4 -1 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 2 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -3 2 -1 2 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 2 -3\\n2 1 2\\n2 3 5\\n\", \"6 4\\n0 -9 4 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 2 2\\n2 3 3\\n\", \"4 4\\n2 -1000 110 3\\n4 1\\n3 2\\n4 2\\n2 2 3\\n2 2 2\\n1 1 -1000000000\\n2 1 4\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n1 4\\n5 6\\n4 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 2\\n2 5 2\\n\", \"6 4\\n0 -9 4 0 14 1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 2\\n2 2 3\\n\", \"6 4\\n3 -9 2 -1 4 0\\n1 5\\n5 4\\n4 6\\n6 2\\n6 3\\n1 2 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"2 1\\n-651044801 1010000100\\n2 1\\n2 1 2\\n\", \"6 4\\n0 -9 0 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 2\\n2 3 5\\n\", \"6 4\\n0 -6 2 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -9 4 0 0 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 3\\n10 -15 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 3\\n0 -9 2 0 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 5\\n2 2 3\\n\", \"6 4\\n10 -9 2 -1 3 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 4 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"4 4\\n2 -1000 110 4\\n4 1\\n3 2\\n4 2\\n2 2 3\\n2 2 2\\n1 1 -1000000000\\n2 1 4\\n\", \"6 4\\n0 -9 4 0 14 1\\n1 5\\n5 4\\n5 6\\n1 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 2\\n2 2 3\\n\", \"6 4\\n0 -9 0 0 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 2\\n2 3 5\\n\", \"6 3\\n10 -21 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n0 -6 4 0 14 1\\n1 5\\n5 4\\n5 6\\n1 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 2\\n2 2 3\\n\", \"6 3\\n10 -21 2 -1 4 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 3\\n10 -21 2 -1 4 -9\\n1 5\\n5 4\\n5 6\\n1 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 3\\n10 -21 2 -1 4 -9\\n1 5\\n5 4\\n5 6\\n1 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 2 3\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 6\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 3\\n0 -9 2 -1 4 -5\\n1 5\\n2 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 4\\n2 3 3\\n\", \"2 1\\n-1000000000 1010001000\\n2 1\\n2 1 2\\n\", \"6 4\\n0 -9 2 -1 4 -3\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 2\\n\", \"6 4\\n0 -9 3 -1 2 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n1 -9 4 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 4\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n1 3 2\\n\", \"6 4\\n0 -9 4 -1 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n-1 -9 2 -1 4 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -3 2 -1 2 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 2 -3\\n2 1 2\\n2 3 6\\n\", \"6 4\\n0 -9 4 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 3 6\\n\", \"6 3\\n0 -9 4 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -12 4 0 14 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -3 2 -1 2 -12\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 3\\n1 1 -3\\n2 1 4\\n2 3 3\\n\", \"6 4\\n10 -9 4 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n10 -9 1 -1 4 -6\\n1 5\\n2 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 3 1\\n\", \"6 4\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 4\\n2 3 6\\n\", \"6 4\\n0 -9 2 -1 1 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 0\\n2 1 2\\n2 5 2\\n\", \"6 4\\n0 -14 4 -1 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 1 3\\n\", \"6 4\\n0 -3 2 -1 3 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n10 -9 1 -1 0 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n1 3 3\\n\", \"6 4\\n10 -9 2 -1 6 -6\\n1 5\\n5 4\\n4 6\\n6 2\\n6 3\\n1 2 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n1 -9 2 -1 1 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -1\\n2 1 2\\n2 5 2\\n\", \"6 4\\n0 -9 4 0 14 1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 2\\n2 2 3\\n\", \"6 4\\n0 -3 2 -1 2 0\\n1 5\\n1 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 4\\n2 4 3\\n\", \"6 4\\n0 -3 2 -1 2 0\\n1 5\\n1 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 5\\n2 3 6\\n\", \"6 4\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 4\\n2 4 3\\n\", \"6 4\\n10 -9 2 -1 0 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 3 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 0 -1 4 -5\\n1 6\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -25 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 1 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -3 2 -1 2 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -9 4 1 0 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -9 3 0 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 4\\n2 3 3\\n\", \"6 4\\n0 -14 4 -1 8 -3\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 2 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -3 2 -1 2 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 2 -3\\n2 1 2\\n2 1 5\\n\", \"4 4\\n2 -1350 110 3\\n4 1\\n3 2\\n4 2\\n2 2 3\\n2 2 2\\n1 1 -1000000000\\n2 1 4\\n\", \"6 4\\n0 -9 2 -1 7 -6\\n1 5\\n1 4\\n5 6\\n4 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 2\\n2 5 2\\n\", \"6 4\\n0 -9 4 0 14 1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 2 -4\\n2 1 2\\n2 2 3\\n\", \"6 3\\n0 -17 2 -1 4 -5\\n1 5\\n3 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -6\\n2 1 4\\n1 3 3\\n\", \"6 4\\n0 -9 4 0 0 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 4 2\\n2 2 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n5 2\\n2 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 5 2\\n\", \"6 4\\n3 -2 2 -1 4 0\\n1 5\\n5 4\\n4 6\\n6 2\\n6 3\\n1 2 4\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 3\\n0 -17 2 -1 4 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 -6\\n2 1 4\\n1 3 3\\n\", \"6 4\\n0 -8 0 0 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 2\\n2 3 5\\n\", \"6 3\\n10 -21 2 -1 4 -6\\n1 5\\n5 4\\n5 2\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n10 -9 2 -1 3 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 3 2\\n1 4 -3\\n2 1 2\\n2 4 3\\n\", \"6 4\\n0 -6 4 0 14 1\\n1 6\\n5 4\\n5 6\\n1 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 2\\n2 2 3\\n\", \"6 3\\n0 -17 2 -1 4 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -6\\n2 2 4\\n1 2 3\\n\", \"6 3\\n10 -21 2 -1 4 -9\\n1 4\\n5 4\\n5 6\\n1 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 3\\n10 -21 2 -1 8 -9\\n1 5\\n5 4\\n5 6\\n1 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 2 3\\n2 3 3\\n\", \"6 3\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 5\\n0 2 3\\n\", \"6 4\\n0 -9 3 -1 2 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 6\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n1 -9 4 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -6\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 1 2\\n1 4 -4\\n2 1 2\\n1 3 3\\n\", \"6 4\\n-1 -9 2 -1 0 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -3 2 -1 2 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 3 -3\\n2 1 2\\n2 3 6\\n\", \"6 4\\n0 -9 4 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 6\\n\", \"6 3\\n0 -9 4 0 8 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 1\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n4 -9 4 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 3 2\\n2 3 1\\n\", \"6 4\\n0 -1 2 -1 1 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 0\\n2 1 2\\n2 5 2\\n\", \"6 4\\n19 -9 1 -1 0 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n1 3 3\\n\", \"6 4\\n0 -9 2 0 14 1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 1 2\\n2 2 3\\n\", \"6 4\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -4\\n2 1 4\\n2 5 3\\n\", \"6 4\\n-1 -9 2 0 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 5\\n1 1 -3\\n2 2 2\\n2 3 3\\n\", \"6 4\\n10 -25 2 -1 4 -11\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 1 2\\n1 4 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 2 0 8 -4\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -9 4 1 -1 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"4 4\\n2 -2609 110 3\\n4 1\\n3 2\\n4 2\\n2 2 3\\n2 2 2\\n1 1 -1000000000\\n2 1 4\\n\", \"6 4\\n0 -9 3 -1 2 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 6\\n1 1 -3\\n2 1 2\\n2 3 5\\n\", \"6 4\\n13 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 1 2\\n1 3 -3\\n2 1 2\\n2 2 3\\n\", \"6 4\\n1 -9 4 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -6\\n2 1 2\\n2 2 3\\n\", \"6 4\\n-1 -9 2 -1 0 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -3 2 -1 2 -6\\n1 4\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 3 -3\\n2 1 2\\n2 3 6\\n\", \"6 4\\n4 -9 4 -1 4 -6\\n1 2\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n1 -1 2 -1 1 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 0\\n2 1 2\\n2 5 2\\n\", \"6 4\\n0 -10 3 0 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 -4\\n2 1 4\\n2 3 3\\n\", \"6 4\\n0 -17 2 -1 4 -16\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 -6\\n2 1 4\\n1 3 3\\n\", \"6 4\\n10 -9 2 -1 3 -1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n1 3 2\\n1 4 -3\\n2 1 2\\n2 4 4\\n\", \"6 4\\n-1 -9 2 -1 0 -9\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 -3\\n2 1 2\\n2 3 5\\n\", \"6 3\\n0 -7 4 -1 10 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n4 -9 4 -1 4 -6\\n1 2\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -2\\n2 1 3\\n2 3 3\\n\", \"6 4\\n19 -3 1 -1 0 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n1 1 3\\n\", \"6 4\\n0 -10 3 0 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 -4\\n2 1 4\\n2 1 3\\n\", \"6 4\\n10 -9 2 -1 3 -1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 3 2\\n1 4 -3\\n2 1 2\\n2 4 4\\n\", \"6 3\\n0 -7 4 -1 10 -3\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -16 2 -1 4 -23\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 3\\n1 1 -6\\n2 1 4\\n1 3 3\\n\", \"6 4\\n10 -9 2 -1 3 -1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 3 2\\n1 4 -3\\n2 2 2\\n2 4 4\\n\", \"6 4\\n10 -9 2 -1 3 -1\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 3 2\\n1 4 -3\\n1 2 2\\n2 4 4\\n\", \"4 4\\n3 -1000 100 3\\n2 1\\n3 2\\n4 1\\n2 1 3\\n2 2 2\\n1 1 -1000000000\\n2 1 4\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 4\\n2 3 2\\n\", \"6 3\\n0 -5 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n1 1 4\\n2 2 3\\n\", \"6 4\\n10 -9 2 -1 2 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 2 -5\\n2 1 2\\n2 3 3\\n\", \"6 4\\n0 -9 4 0 11 0\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 2 3\\n\", \"6 4\\n0 -3 2 -1 2 -12\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 2 2\\n1 1 -5\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -1 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 3\\n2 3 3\\n\", \"6 4\\n0 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 2 2\\n2 3 4\\n\", \"6 4\\n0 -9 2 -1 4 -5\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 5\\n1 1 -4\\n2 1 4\\n2 3 3\\n\", \"4 4\\n2 -1000 100 3\\n2 1\\n3 2\\n4 2\\n2 2 3\\n2 2 2\\n1 2 -1000000000\\n2 1 4\\n\", \"6 4\\n0 -4 2 -1 4 -2\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 4\\n1 1 -3\\n2 1 2\\n2 3 3\\n\", \"6 4\\n10 -9 2 -1 4 -6\\n1 5\\n5 4\\n5 6\\n6 2\\n6 3\\n2 1 2\\n1 1 -3\\n2 1 2\\n2 3 3\\n\"], \"outputs\": [\"2000000000\\n\", \"2102\\n0\\n1000000003\\n\", \"19\\n32\\n0\\n\", \"9\\n32\\n0\\n\", \"9\\n30\\n0\\n\", \"9\\n12\\n0\\n\", \"9\\n12\\n\", \"2010000000\\n\", \"2102\\n0\\n1000002003\\n\", \"39\\n33\\n0\\n\", \"9\\n32\\n23\\n\", \"25\\n0\\n\", \"9\\n32\\n25\\n\", \"9\\n0\\n0\\n\", \"35\\n29\\n0\\n\", \"9\\n32\\n\", \"31\\n0\\n\", \"3\\n26\\n22\\n\", \"17\\n40\\n0\\n\", \"9\\n38\\n0\\n\", \"0\\n29\\n0\\n\", \"17\\n0\\n0\\n\", \"16\\n0\\n0\\n\", \"0\\n19\\n0\\n\", \"16\\n0\\n25\\n\", \"0\\n22\\n0\\n\", \"16\\n0\\n13\\n\", \"0\\n34\\n0\\n\", \"28\\n0\\n13\\n\", \"0\\n8\\n0\\n\", \"39\\n25\\n0\\n\", \"9\\n13\\n0\\n\", \"8\\n11\\n\", \"1100\\n0\\n1000002003\\n\", \"9\\n22\\n15\\n\", \"1\\n4\\n\", \"21\\n32\\n\", \"9\\n30\\n5\\n\", \"32\\n0\\n\", \"3\\n23\\n22\\n\", \"17\\n45\\n0\\n\", \"9\\n24\\n0\\n\", \"0\\n7\\n0\\n\", \"37\\n0\\n25\\n\", \"0\\n21\\n0\\n\", \"28\\n0\\n15\\n\", \"19\\n32\\n\", \"21\\n0\\n0\\n\", \"1100\\n0\\n1000000003\\n\", \"1\\n14\\n21\\n\", \"19\\n30\\n\", \"38\\n0\\n\", \"3\\n24\\n22\\n\", \"19\\n12\\n\", \"28\\n42\\n15\\n\", \"0\\n4\\n0\\n\", \"1\\n5\\n9\\n\", \"26\\n0\\n\", \"0\\n5\\n0\\n\", \"5\\n5\\n0\\n\", \"2000000010\\n\", \"9\\n22\\n0\\n\", \"9\\n12\\n21\\n\", \"1661044801\\n\", \"10\\n0\\n0\\n\", \"9\\n15\\n\", \"35\\n35\\n0\\n\", \"9\\n31\\n\", \"28\\n30\\n0\\n\", \"35\\n0\\n\", \"0\\n26\\n22\\n\", \"0\\n35\\n0\\n\", \"16\\n0\\n23\\n\", \"17\\n0\\n13\\n\", \"0\\n0\\n13\\n\", \"45\\n25\\n0\\n\", \"8\\n12\\n\", \"39\\n0\\n\", \"17\\n31\\n0\\n\", \"0\\n7\\n4\\n\", \"37\\n0\\n0\\n\", \"1110\\n0\\n1000000003\\n\", \"10\\n14\\n21\\n\", \"28\\n43\\n15\\n\", \"19\\n0\\n\", \"1661044901\\n\", \"28\\n30\\n14\\n\", \"16\\n0\\n20\\n\", \"9\\n0\\n13\\n\", \"45\\n25\\n\", \"8\\n8\\n\", \"37\\n0\\n\", \"1110\\n0\\n1000000004\\n\", \"28\\n13\\n51\\n\", \"27\\n30\\n14\\n\", \"51\\n25\\n\", \"28\\n10\\n48\\n\", \"57\\n31\\n\", \"31\\n31\\n\", \"31\\n55\\n\", \"21\\n24\\n0\\n\", \"37\\n40\\n\", \"2010001000\\n\", \"9\\n26\\n17\\n\", \"5\\n26\\n0\\n\", \"10\\n32\\n0\\n\", \"1\\n34\\n\", \"17\\n35\\n0\\n\", \"10\\n38\\n0\\n\", \"0\\n29\\n8\\n\", \"16\\n0\\n10\\n\", \"16\\n0\\n\", \"28\\n0\\n16\\n\", \"29\\n8\\n0\\n\", \"39\\n27\\n0\\n\", \"49\\n32\\n0\\n\", \"9\\n0\\n25\\n\", \"9\\n13\\n7\\n\", \"16\\n23\\n22\\n\", \"17\\n45\\n35\\n\", \"0\\n23\\n0\\n\", \"11\\n24\\n\", \"42\\n0\\n\", \"4\\n24\\n22\\n\", \"39\\n42\\n15\\n\", \"0\\n4\\n13\\n\", \"0\\n5\\n2\\n\", \"9\\n13\\n21\\n\", \"31\\n31\\n0\\n\", \"28\\n22\\n0\\n\", \"47\\n0\\n\", \"0\\n28\\n0\\n\", \"37\\n0\\n23\\n\", \"1\\n0\\n13\\n\", \"8\\n12\\n0\\n\", \"17\\n25\\n0\\n\", \"0\\n7\\n2\\n\", \"1460\\n0\\n1000000003\\n\", \"10\\n14\\n24\\n\", \"28\\n34\\n10\\n\", \"23\\n29\\n\", \"9\\n9\\n13\\n\", \"9\\n20\\n13\\n\", \"21\\n0\\n\", \"28\\n15\\n\", \"26\\n29\\n14\\n\", \"39\\n67\\n\", \"37\\n23\\n\", \"30\\n10\\n20\\n\", \"9\\n44\\n\", \"31\\n33\\n\", \"31\\n63\\n\", \"9\\n7\\n\", \"9\\n26\\n0\\n\", \"10\\n35\\n0\\n\", \"31\\n\", \"2\\n30\\n0\\n\", \"0\\n29\\n9\\n\", \"16\\n0\\n15\\n\", \"0\\n0\\n\", \"33\\n27\\n0\\n\", \"9\\n23\\n25\\n\", \"16\\n15\\n14\\n\", \"20\\n24\\n\", \"39\\n42\\n13\\n\", \"9\\n13\\n16\\n\", \"5\\n0\\n0\\n\", \"57\\n0\\n\", \"33\\n0\\n19\\n\", \"3\\n0\\n13\\n\", \"2719\\n0\\n1000000003\\n\", \"9\\n26\\n15\\n\", \"31\\n24\\n\", \"10\\n35\\n25\\n\", \"21\\n30\\n0\\n\", \"0\\n31\\n9\\n\", \"13\\n37\\n0\\n\", \"17\\n15\\n14\\n\", \"21\\n12\\n0\\n\", \"42\\n15\\n\", \"27\\n0\\n\", \"21\\n30\\n20\\n\", \"21\\n42\\n\", \"13\\n36\\n0\\n\", \"20\\n18\\n\", \"21\\n12\\n25\\n\", \"13\\n27\\n0\\n\", \"21\\n36\\n\", \"56\\n15\\n\", \"13\\n0\\n0\\n\", \"13\\n0\\n\", \"2103\\n0\\n1000000003\\n\", \"9\\n12\\n23\\n\", \"9\\n\", \"0\\n31\\n0\\n\", \"22\\n0\\n13\\n\", \"0\\n36\\n0\\n\", \"31\\n25\\n0\\n\", \"9\\n0\\n23\\n\", \"4\\n13\\n0\\n\", \"1100\\n0\\n2000000005\\n\", \"9\\n19\\n0\\n\", \"39\\n32\\n0\\n\"]}", "source": "taco"}
|
Chanek Jones is back, helping his long-lost relative Indiana Jones, to find a secret treasure in a maze buried below a desert full of illusions.
The map of the labyrinth forms a tree with n rooms numbered from 1 to n and n - 1 tunnels connecting them such that it is possible to travel between each pair of rooms through several tunnels.
The i-th room (1 ≤ i ≤ n) has a_i illusion rate. To go from the x-th room to the y-th room, there must exist a tunnel between x and y, and it takes max(|a_x + a_y|, |a_x - a_y|) energy. |z| denotes the absolute value of z.
To prevent grave robbers, the maze can change the illusion rate of any room in it. Chanek and Indiana would ask q queries.
There are two types of queries to be done:
* 1\ u\ c — The illusion rate of the x-th room is changed to c (1 ≤ u ≤ n, 0 ≤ |c| ≤ 10^9).
* 2\ u\ v — Chanek and Indiana ask you the minimum sum of energy needed to take the secret treasure at room v if they are initially at room u (1 ≤ u, v ≤ n).
Help them, so you can get a portion of the treasure!
Input
The first line contains two integers n and q (2 ≤ n ≤ 10^5, 1 ≤ q ≤ 10^5) — the number of rooms in the maze and the number of queries.
The second line contains n integers a_1, a_2, …, a_n (0 ≤ |a_i| ≤ 10^9) — inital illusion rate of each room.
The i-th of the next n-1 lines contains two integers s_i and t_i (1 ≤ s_i, t_i ≤ n), meaning there is a tunnel connecting s_i-th room and t_i-th room. The given edges form a tree.
The next q lines contain the query as described. The given queries are valid.
Output
For each type 2 query, output a line containing an integer — the minimum sum of energy needed for Chanek and Indiana to take the secret treasure.
Example
Input
6 4
10 -9 2 -1 4 -6
1 5
5 4
5 6
6 2
6 3
2 1 2
1 1 -3
2 1 2
2 3 3
Output
39
32
0
Note
<image>
In the first query, their movement from the 1-st to the 2-nd room is as follows.
* 1 → 5 — takes max(|10 + 4|, |10 - 4|) = 14 energy.
* 5 → 6 — takes max(|4 + (-6)|, |4 - (-6)|) = 10 energy.
* 6 → 2 — takes max(|-6 + (-9)|, |-6 - (-9)|) = 15 energy.
In total, it takes 39 energy.
In the second query, the illusion rate of the 1-st room changes from 10 to -3.
In the third query, their movement from the 1-st to the 2-nd room is as follows.
* 1 → 5 — takes max(|-3 + 4|, |-3 - 4|) = 7 energy.
* 5 → 6 — takes max(|4 + (-6)|, |4 - (-6)|) = 10 energy.
* 6 → 2 — takes max(|-6 + (-9)|, |-6 - (-9)|) = 15 energy.
Now, it takes 32 energy.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.625
|
{"tests": "{\"inputs\": [\"6 7\", \"12 2\", \"16 38\", \"1 7\", \"12 1\", \"16 25\", \"2 7\", \"12 0\", \"16 29\", \"2 9\", \"16 46\", \"3 9\", \"16 31\", \"4 9\", \"27 31\", \"4 18\", \"27 51\", \"4 10\", \"27 102\", \"1 10\", \"42 102\", \"42 123\", \"46 123\", \"70 123\", \"70 2\", \"121 2\", \"63 2\", \"63 4\", \"63 7\", \"118 7\", \"118 8\", \"118 5\", \"112 5\", \"111 5\", \"101 5\", \"101 7\", \"101 2\", \"101 3\", \"001 5\", \"001 3\", \"4 14\", \"12 17\", \"16 26\", \"14 2\", \"6 38\", \"1 4\", \"1 25\", \"2 4\", \"5 29\", \"2 12\", \"32 46\", \"3 12\", \"19 31\", \"27 40\", \"8 18\", \"10 51\", \"6 10\", \"28 51\", \"2 10\", \"42 140\", \"42 89\", \"46 178\", \"65 123\", \"70 3\", \"217 2\", \"106 7\", \"159 7\", \"118 12\", \"236 5\", \"137 5\", \"110 5\", \"101 6\", \"100 5\", \"4 5\", \"19 17\", \"7 26\", \"23 2\", \"6 66\", \"1 23\", \"4 4\", \"22 2\", \"5 53\", \"4 12\", \"13 46\", \"3 5\", \"19 11\", \"27 33\", \"8 12\", \"10 45\", \"6 11\", \"28 80\", \"42 148\", \"42 116\", \"87 178\", \"46 189\", \"217 3\", \"3 8\", \"62 7\", \"159 6\", \"57 12\", \"4 7\", \"12 20\", \"16 30\"], \"outputs\": [\"709\\n\", \"12\\n\", \"764202521\\n\", \"13\\n\", \"1\\n\", \"378000346\\n\", \"33\\n\", \"0\\n\", \"396835115\\n\", \"88\\n\", \"942083119\\n\", \"221\\n\", \"656835898\\n\", \"530\\n\", \"913187911\\n\", \"46135\\n\", \"171253160\\n\", \"894\\n\", \"95990504\\n\", \"55\\n\", \"184174004\\n\", \"268300608\\n\", \"960087486\\n\", \"396400358\\n\", \"70\\n\", \"121\\n\", \"63\\n\", \"43744\\n\", \"110221970\\n\", \"265217321\\n\", \"623198304\\n\", \"8502551\\n\", \"6919782\\n\", \"6679205\\n\", \"4603380\\n\", \"712445980\\n\", \"101\\n\", \"5152\\n\", \"5\\n\", \"2\\n\", \"6610\\n\", \"30428254\\n\", \"628689768\\n\", \"14\\n\", \"814411873\\n\", \"3\\n\", \"75025\\n\", \"7\\n\", \"24151764\\n\", \"376\\n\", \"243159255\\n\", \"972\\n\", \"857741519\\n\", \"748837192\\n\", \"1914166\\n\", \"908007918\\n\", \"4685\\n\", \"905338544\\n\", \"143\\n\", \"918023453\\n\", \"858419444\\n\", \"108507677\\n\", \"70310907\\n\", \"2486\\n\", \"217\\n\", \"273533523\\n\", \"705739858\\n\", \"677962323\\n\", \"132591705\\n\", \"15339207\\n\", \"6444957\\n\", \"96742853\\n\", \"4426427\\n\", \"51\\n\", \"304531348\\n\", \"38839257\\n\", \"23\\n\", \"258771290\\n\", \"28657\\n\", \"25\\n\", \"22\\n\", \"135669311\\n\", \"2462\\n\", \"979039299\\n\", \"26\\n\", \"15586342\\n\", \"389828771\\n\", \"70954\\n\", \"719146023\\n\", \"8273\\n\", \"581183487\\n\", \"141518664\\n\", \"454129300\\n\", \"14457793\\n\", \"727461433\\n\", \"23654\\n\", \"133\\n\", \"100518497\\n\", \"901985273\\n\", \"107563736\\n\", \"176\", \"174174144\", \"102292850\"]}", "source": "taco"}
|
E869120 defined a sequence $a$ like this:
* $a_1=a_2=1$, $a_{k+2}=a_{k+1}+a_k \ (k \ge 1)$
He also defined sequences $d_1, d_2, d_3, \dots , d_n$, as the following recurrence relation :
* $d_{1, j} = a_j$
* $d_{i, j} = \sum_{k = 1}^j d_{i - 1, k} \ (i \ge 2)$
You are given integers $n$ and $m$. Please calculate the value of $d_{n, m}$.
Since the answer can be large number, print the answer modulo $998,244,353$.
Can you solve this problem???
Input
The input is given from standard input in the following format.
> $n \quad m$
Output
* Print $d_{n, m}$ modulo $998,244,353$.
Constraints
* $1 \le n \le 200,000$
* $1 \le m \le 10^{18}$
Subtasks
Subtask 1 [ $100$ points ]
* The testcase in this subtask satisfies $1 \le n, m \le 3,000$.
Subtask 2 [ $170$ points ]
* The testcase in this subtask satisfies $1 \le m \le 200,000$.
Subtask 3 [ $230$ points ]
* The testcase in this subtask satisfies $1 \le n \le 3$.
Subtask 4 [ $420$ points ]
* The testcase in this subtask satisfies $1 \le n \le 1000$.
Subtask 5 [ $480$ points ]
* There are no additional constraints.
Output
* Print $d_{n, m}$ modulo $998,244,353$.
Constraints
* $1 \le n \le 200,000$
* $1 \le m \le 10^{18}$
Subtasks
Subtask 1 [ $100$ points ]
* The testcase in this subtask satisfies $1 \le n, m \le 3,000$.
Subtask 2 [ $170$ points ]
* The testcase in this subtask satisfies $1 \le m \le 200,000$.
Subtask 3 [ $230$ points ]
* The testcase in this subtask satisfies $1 \le n \le 3$.
Subtask 4 [ $420$ points ]
* The testcase in this subtask satisfies $1 \le n \le 1000$.
Subtask 5 [ $480$ points ]
* There are no additional constraints.
Input
The input is given from standard input in the following format.
> $n \quad m$
Examples
Input
4 7
Output
176
Input
12 20
Output
174174144
Input
16 30
Output
102292850
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4\\n0 0 0\\n2 0 0\\n2 2 0\\n0 2 0\\n4\\n1 1 -1\\n1 1 1\\n1 3 1\\n1 3 -1\\n\", \"4\\n4 -2 0\\n4 3 0\\n-3 3 0\\n-3 -2 0\\n4\\n6 -2 0\\n3 2 2\\n-3 7 0\\n3 4 6\\n\", \"4\\n-6 6 0\\n13 9 0\\n15 -7 0\\n-5 -5 0\\n4\\n2 0 4\\n2 6 8\\n2 12 1\\n2 4 -4\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 8\\n4\\n-10 5 0\\n25 18 0\\n23 8 0\\n-9 0 0\\n\", \"4\\n-10 5 0\\n25 18 0\\n23 8 0\\n-9 0 0\\n5\\n7 12 -5\\n7 0 -10\\n7 3 8\\n7 10 7\\n7 6 0\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1000 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n150 1200 -900\\n-1514 1340 0\\n582 -454 1098\\n\", \"8\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1000 0\\n1500 0 0\\n0 0 0\\n8\\n-200 1000 400\\n150 1000 400\\n125 250 -500\\n850 250 -500\\n750 1000 400\\n1200 1000 400\\n1250 0 -800\\n-250 0 -800\\n\", \"4\\n3390 -1280 0\\n1500 -200 -1000\\n-950 1200 0\\n1500 -200 1650\\n9\\n2500 900 0\\n500 1200 0\\n-600 1000 0\\n100 600 0\\n-2000 700 0\\n3500 -2500 0\\n3750 -550 0\\n2410 -720 0\\n600 -400 0\\n\", \"4\\n0 1000 -700\\n1500 1000 -700\\n1500 1000 500\\n0 1000 500\\n5\\n0 500 0\\n1500 1500 0\\n0 1500 0\\n250 1000 0\\n500 1000 0\\n\", \"9\\n1824 1717 0\\n573 1114 0\\n-850 0 0\\n0 0 0\\n949 665 0\\n3700 -1200 0\\n3639 485 0\\n2500 0 0\\n2741 578 0\\n7\\n1300 0 -1000\\n-800 0 -1000\\n-1500 0 0\\n-1087 0 1400\\n470 0 0\\n740 0 1800\\n3320 0 0\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n2600 500 0\\n900 500 0\\n900 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 150 0\\n2350 150 0\\n2350 -1750 0\\n900 -1750 0\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n3100 -750 500\\n\", \"9\\n2564 865 0\\n573 1115 0\\n-600 1000 0\\n100 600 0\\n949 665 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n280 60 900\\n1990 -480 0\\n1710 -320 0\\n830 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -777\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n2294 700 -439\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -975\\n-294 700 -777\\n\", \"4\\n4 -2 0\\n4 3 0\\n-3 3 0\\n-3 -2 0\\n4\\n6 -2 0\\n3 2 2\\n-3 7 0\\n3 4 6\\n\", \"4\\n-10 5 0\\n25 18 0\\n23 8 0\\n-9 0 0\\n5\\n7 12 -5\\n7 0 -10\\n7 3 8\\n7 10 7\\n7 6 0\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1000 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n150 1200 -900\\n-1514 1340 0\\n582 -454 1098\\n\", \"4\\n0 1000 -700\\n1500 1000 -700\\n1500 1000 500\\n0 1000 500\\n5\\n0 500 0\\n1500 1500 0\\n0 1500 0\\n250 1000 0\\n500 1000 0\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n2600 500 0\\n900 500 0\\n900 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 150 0\\n2350 150 0\\n2350 -1750 0\\n900 -1750 0\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n3100 -750 500\\n\", \"8\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1000 0\\n1500 0 0\\n0 0 0\\n8\\n-200 1000 400\\n150 1000 400\\n125 250 -500\\n850 250 -500\\n750 1000 400\\n1200 1000 400\\n1250 0 -800\\n-250 0 -800\\n\", \"4\\n-6 6 0\\n13 9 0\\n15 -7 0\\n-5 -5 0\\n4\\n2 0 4\\n2 6 8\\n2 12 1\\n2 4 -4\\n\", \"9\\n1824 1717 0\\n573 1114 0\\n-850 0 0\\n0 0 0\\n949 665 0\\n3700 -1200 0\\n3639 485 0\\n2500 0 0\\n2741 578 0\\n7\\n1300 0 -1000\\n-800 0 -1000\\n-1500 0 0\\n-1087 0 1400\\n470 0 0\\n740 0 1800\\n3320 0 0\\n\", \"9\\n2564 865 0\\n573 1115 0\\n-600 1000 0\\n100 600 0\\n949 665 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n280 60 900\\n1990 -480 0\\n1710 -320 0\\n830 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n2294 700 -439\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -975\\n-294 700 -777\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 8\\n4\\n-10 5 0\\n25 18 0\\n23 8 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -777\\n\", \"4\\n3390 -1280 0\\n1500 -200 -1000\\n-950 1200 0\\n1500 -200 1650\\n9\\n2500 900 0\\n500 1200 0\\n-600 1000 0\\n100 600 0\\n-2000 700 0\\n3500 -2500 0\\n3750 -550 0\\n2410 -720 0\\n600 -400 0\\n\", \"4\\n4 -2 0\\n4 3 0\\n-3 3 0\\n-3 -4 0\\n4\\n6 -2 0\\n3 2 2\\n-3 7 0\\n3 4 6\\n\", \"8\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1000 0\\n1500 0 0\\n0 0 0\\n8\\n-200 1000 400\\n150 1000 400\\n125 250 -500\\n850 250 -500\\n750 1000 400\\n1200 1000 400\\n1250 0 -800\\n-450 0 -800\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1000 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n150 1200 -900\\n-1514 2189 0\\n582 -454 1098\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n2600 500 0\\n900 500 0\\n900 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 150 0\\n2350 150 0\\n2350 -1750 0\\n900 -1750 -1\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n3100 -750 500\\n\", \"9\\n2564 865 0\\n573 1115 0\\n-600 1000 0\\n100 600 0\\n949 665 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n89 60 900\\n1990 -480 0\\n1710 -320 0\\n830 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n2294 700 -439\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 10\\n4\\n-10 5 0\\n25 18 0\\n23 8 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -1004\\n\", \"4\\n3390 -1872 0\\n1500 -200 -1000\\n-950 1200 0\\n1500 -200 1650\\n9\\n2500 900 0\\n500 1200 0\\n-600 1000 0\\n100 600 0\\n-2000 700 0\\n3500 -2500 0\\n3750 -550 0\\n2410 -720 0\\n600 -400 0\\n\", \"4\\n4 -2 -1\\n4 3 0\\n-3 3 0\\n-3 -4 0\\n4\\n6 -2 0\\n3 2 2\\n-3 7 0\\n3 4 6\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1001 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n150 1200 -900\\n-1514 2189 0\\n582 -454 1098\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n641 500 0\\n900 500 0\\n900 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 150 0\\n2350 150 0\\n2350 -1750 0\\n900 -1750 -1\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n3100 -750 500\\n\", \"8\\n-1 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1000 0\\n1500 0 0\\n0 0 0\\n8\\n-200 1000 400\\n150 1000 400\\n125 250 -500\\n850 250 -500\\n750 1000 400\\n1200 1000 400\\n1250 0 -800\\n-450 0 -800\\n\", \"9\\n2564 865 0\\n573 820 0\\n-600 1000 0\\n100 600 0\\n949 665 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n89 60 900\\n1990 -480 0\\n1710 -320 0\\n830 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n2294 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 10\\n4\\n-10 10 0\\n25 18 0\\n23 8 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 676 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -1004\\n\", \"4\\n3390 -1872 0\\n1500 -200 -1000\\n-950 1200 0\\n1500 -200 1650\\n9\\n2500 561 0\\n500 1200 0\\n-600 1000 0\\n100 600 0\\n-2000 700 0\\n3500 -2500 0\\n3750 -550 0\\n2410 -720 0\\n600 -400 0\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1001 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n150 1200 -900\\n-1514 2189 0\\n582 -454 1144\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 662\\n1173 700 -339\\n2294 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"3\\n2 16 0\\n8 -6 -8\\n14 3 10\\n4\\n-10 10 0\\n25 18 0\\n23 8 0\\n-9 0 0\\n\", \"4\\n3390 -1872 0\\n1500 -200 -1000\\n-950 1200 0\\n1500 -200 98\\n9\\n2500 561 0\\n500 1200 0\\n-600 1000 0\\n100 600 0\\n-2000 700 0\\n3500 -2500 0\\n3750 -550 0\\n2410 -720 0\\n600 -400 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 662\\n1173 700 -339\\n2187 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n1 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 662\\n1173 700 -339\\n2187 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n1 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 662\\n1173 700 -339\\n2187 700 -243\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"4\\n4 -2 0\\n4 3 0\\n-3 3 0\\n-3 -2 1\\n4\\n6 -2 0\\n3 2 2\\n-3 7 0\\n3 4 6\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n2600 500 0\\n1447 500 0\\n900 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 150 0\\n2350 150 0\\n2350 -1750 0\\n900 -1750 0\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n3100 -750 500\\n\", \"4\\n-6 6 0\\n13 9 0\\n15 0 0\\n-5 -5 0\\n4\\n2 0 4\\n2 6 8\\n2 12 1\\n2 4 -4\\n\", \"9\\n2564 865 0\\n774 1115 0\\n-600 1000 0\\n100 600 0\\n949 665 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n280 60 900\\n1990 -480 0\\n1710 -320 0\\n830 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 669 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n2294 700 -439\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -975\\n-294 700 -777\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 8\\n4\\n-10 5 0\\n25 18 0\\n23 14 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -196\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -777\\n\", \"4\\n4 -2 0\\n4 3 0\\n-3 3 0\\n-3 -4 0\\n4\\n6 -2 0\\n5 2 2\\n-3 7 0\\n3 4 6\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1000 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n269 1200 -900\\n-1514 2189 0\\n582 -454 1098\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n2600 500 0\\n900 500 0\\n900 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 170 0\\n2350 150 0\\n2350 -1750 0\\n900 -1750 -1\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n3100 -750 500\\n\", \"8\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 150 0\\n1000 1000 0\\n1401 1000 0\\n1500 0 0\\n0 0 0\\n8\\n-200 1000 400\\n150 1000 400\\n125 250 -500\\n850 250 -500\\n750 1000 400\\n1200 1000 400\\n1250 0 -800\\n-450 0 -800\\n\", \"9\\n2564 865 0\\n573 1115 0\\n-600 1000 0\\n100 600 0\\n949 721 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n89 60 900\\n1990 -480 0\\n1710 -320 0\\n830 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n2294 700 -439\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 370\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 10\\n4\\n-10 5 0\\n25 18 0\\n23 14 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3161 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -1004\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1001 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n181 1200 -900\\n-1514 2189 0\\n582 -454 1098\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n641 500 0\\n900 500 0\\n900 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 150 0\\n2177 150 0\\n2350 -1750 0\\n900 -1750 -1\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n3100 -750 500\\n\", \"8\\n-1 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1000 0\\n1500 0 0\\n0 0 0\\n8\\n-200 1000 400\\n150 1000 400\\n125 250 -500\\n850 250 -500\\n750 1000 400\\n1200 1000 400\\n1250 0 -800\\n-541 0 -800\\n\", \"9\\n2564 865 0\\n573 820 0\\n-600 1000 0\\n100 600 0\\n949 665 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n89 60 900\\n1990 -480 0\\n1710 -320 0\\n830 825 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1444 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n2294 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"3\\n2 16 0\\n16 -6 -8\\n8 3 10\\n4\\n-10 10 0\\n25 18 0\\n23 8 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 676 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n197 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -1004\\n\", \"4\\n3390 -1872 0\\n1500 -200 -1000\\n-950 1200 0\\n1500 -200 1650\\n9\\n2500 561 0\\n500 1200 0\\n-600 1000 0\\n100 600 0\\n-2000 700 0\\n3500 -2500 0\\n3750 -550 0\\n2410 -563 0\\n600 -400 0\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1001 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n150 1200 -900\\n-1514 2189 1\\n582 -454 1144\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 518\\n1131 700 662\\n1173 700 -339\\n2294 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"3\\n2 16 0\\n8 -6 -8\\n14 3 10\\n4\\n-10 10 0\\n25 18 0\\n23 14 0\\n-9 0 0\\n\", \"4\\n3390 -1872 0\\n1500 -200 -1000\\n-950 1200 0\\n1500 -200 98\\n9\\n2500 561 0\\n500 1200 0\\n-600 1000 0\\n100 600 0\\n-843 700 0\\n3500 -2500 0\\n3750 -550 0\\n2410 -720 0\\n600 -400 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 662\\n1173 700 -339\\n2187 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-545 700 -777\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n1 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 662\\n1173 700 -339\\n2187 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-485 700 -777\\n\", \"4\\n4 -2 0\\n4 3 0\\n-4 3 0\\n-3 -2 1\\n4\\n6 -2 0\\n3 2 2\\n-3 7 0\\n3 4 6\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n2600 500 0\\n1447 500 0\\n346 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 150 0\\n2350 150 0\\n2350 -1750 0\\n900 -1750 0\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n3100 -750 500\\n\", \"9\\n2564 865 0\\n774 1115 0\\n-600 1000 0\\n100 600 0\\n949 665 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n280 60 900\\n1990 -480 0\\n1710 -320 0\\n1103 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 8\\n4\\n-10 5 0\\n25 30 0\\n23 14 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -673\\n2847 700 -196\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -777\\n\", \"4\\n4 -2 0\\n4 3 0\\n-3 3 0\\n-3 -4 0\\n4\\n6 -2 0\\n5 2 2\\n-3 7 0\\n3 7 6\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1000 0\\n250 500 0\\n-2267 684 0\\n4\\n1615 -150 0\\n269 1200 -900\\n-1514 2189 0\\n582 -454 1098\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n2600 500 0\\n900 500 0\\n900 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 170 0\\n2350 150 0\\n2350 -1750 0\\n900 -801 -1\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n3100 -750 500\\n\", \"9\\n2564 865 0\\n573 1115 0\\n-254 1000 0\\n100 600 0\\n949 721 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n89 60 900\\n1990 -480 0\\n1710 -320 0\\n830 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 10\\n4\\n-10 5 0\\n25 18 0\\n23 14 0\\n-9 1 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3161 1071 0\\n3754 1 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -1004\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1001 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n181 1200 -900\\n-1514 2189 0\\n582 -213 1098\\n\", \"14\\n900 -2000 0\\n2600 -2000 0\\n641 500 0\\n900 500 0\\n900 -1500 0\\n2200 -1500 0\\n2200 -200 0\\n1900 -300 0\\n1900 -1200 0\\n1100 -1250 0\\n1100 150 0\\n2177 150 0\\n2350 -1750 0\\n900 -1750 -1\\n4\\n3100 -750 -500\\n1500 -750 -500\\n1500 -750 500\\n5922 -750 500\\n\", \"3\\n2 16 1\\n16 -6 -8\\n8 3 10\\n4\\n-10 10 0\\n25 18 0\\n23 8 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 676 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1995 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n197 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -1004\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n1281 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 518\\n1131 700 662\\n1173 700 -339\\n2294 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"3\\n4 16 0\\n8 -6 -8\\n14 3 10\\n4\\n-10 10 0\\n25 18 0\\n23 14 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 776 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n1 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 662\\n1173 700 -339\\n2187 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-485 700 -777\\n\", \"4\\n4 -2 0\\n4 3 0\\n-4 3 0\\n-6 -2 1\\n4\\n6 -2 0\\n3 2 2\\n-3 7 0\\n3 4 6\\n\", \"9\\n2564 865 0\\n774 1115 0\\n-600 1000 0\\n100 600 0\\n949 665 0\\n2341 -298 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n280 60 900\\n1990 -480 0\\n1710 -320 0\\n1103 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 14\\n4\\n-10 5 0\\n25 30 0\\n23 14 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 101 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -673\\n2847 700 -196\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -777\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1000 0\\n250 500 0\\n-1894 684 0\\n4\\n1615 -150 0\\n269 1200 -900\\n-1514 2189 0\\n582 -454 1098\\n\", \"9\\n2564 865 0\\n573 1115 0\\n-452 1000 0\\n100 600 0\\n949 721 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n89 60 900\\n1990 -480 0\\n1710 -320 0\\n830 450 -550\\n660 280 0\\n270 260 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 10\\n4\\n-10 5 0\\n36 18 0\\n23 14 0\\n-9 1 0\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1001 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n181 1200 -900\\n-1514 2189 0\\n582 -141 1098\\n\", \"3\\n2 16 1\\n16 -6 -8\\n8 3 10\\n4\\n-10 10 0\\n25 18 0\\n13 8 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 676 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1995 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n197 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n1269 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -1004\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n1281 1044 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 518\\n1131 700 662\\n1173 700 -339\\n2294 700 -163\\n2238 700 513\\n2711 700 43\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-294 700 -777\\n\", \"3\\n4 16 0\\n8 -6 -8\\n14 3 10\\n4\\n-9 10 0\\n25 18 0\\n23 14 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n509 517 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2086 442 0\\n2079 776 0\\n2506 1032 0\\n2549 450 0\\n3077 446 0\\n3063 1067 0\\n3715 1062 0\\n3756 -125 0\\n1 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 142\\n1173 700 -339\\n2187 700 -163\\n2238 700 513\\n2711 700 500\\n2773 700 -473\\n3374 700 -402\\n3386 700 515\\n3925 700 451\\n3880 700 -957\\n-485 700 -777\\n\", \"4\\n4 -2 0\\n4 3 0\\n0 3 0\\n-6 -2 1\\n4\\n6 -2 0\\n3 2 2\\n-3 7 0\\n3 4 6\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 14\\n4\\n-10 5 0\\n25 30 0\\n23 11 0\\n-9 0 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 101 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n3661 449 0\\n3069 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -673\\n2847 700 -196\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -777\\n\", \"5\\n942 -816 0\\n573 467 0\\n-800 1000 0\\n250 500 0\\n-1894 684 0\\n4\\n1615 -150 0\\n269 1200 -900\\n-1514 2189 0\\n582 -454 1098\\n\", \"9\\n2564 865 0\\n573 1115 0\\n-452 1000 0\\n100 600 0\\n949 721 0\\n2341 -2375 0\\n3879 -561 0\\n2200 -600 0\\n2543 -250 0\\n10\\n2900 -1000 0\\n89 60 900\\n1990 -480 0\\n1710 -320 0\\n830 450 -550\\n660 280 0\\n270 90 500\\n345 460 0\\n-520 1440 -1000\\n1300 400 -1000\\n\", \"3\\n2 13 0\\n8 -6 -8\\n8 3 10\\n4\\n-10 5 0\\n36 18 0\\n23 14 0\\n-9 1 0\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1001 0\\n250 500 0\\n-2012 684 0\\n4\\n1615 -150 0\\n181 1200 -900\\n-1514 229 0\\n582 -141 1098\\n\", \"3\\n2 16 1\\n16 -6 -8\\n8 3 10\\n4\\n-10 10 0\\n25 18 0\\n13 8 0\\n-9 -1 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 500 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 676 0\\n2066 1040 0\\n2492 1031 0\\n2541 449 0\\n3069 451 0\\n3050 1995 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n197 700 397\\n1131 700 572\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -425\\n2847 700 -380\\n1269 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -1004\\n\", \"3\\n4 16 -1\\n8 -6 -8\\n14 3 10\\n4\\n-9 10 0\\n25 18 0\\n23 14 0\\n-9 0 0\\n\", \"4\\n4 -2 0\\n4 3 0\\n0 2 0\\n-6 -2 1\\n4\\n6 -2 0\\n3 2 2\\n-3 7 0\\n3 4 6\\n\", \"3\\n2 16 0\\n8 -6 -8\\n8 3 14\\n4\\n-10 5 0\\n25 30 0\\n23 11 0\\n-9 1 0\\n\", \"16\\n0 1000 0\\n436 1013 0\\n500 500 0\\n1000 101 0\\n1000 1000 0\\n1401 1028 0\\n1434 461 0\\n2087 442 0\\n2066 1040 0\\n2492 1031 0\\n3661 449 0\\n293 451 0\\n3050 1071 0\\n3702 1071 0\\n3754 0 0\\n0 0 0\\n16\\n-243 700 394\\n109 700 365\\n129 700 -366\\n763 700 -366\\n725 700 397\\n1131 700 409\\n1173 700 -339\\n1910 700 -405\\n1834 700 414\\n2254 700 439\\n2323 700 -673\\n2847 700 -196\\n2849 700 477\\n3418 700 470\\n3537 700 -1057\\n-294 700 -777\\n\", \"5\\n942 -816 0\\n197 467 0\\n-800 1000 0\\n250 500 0\\n-1894 684 0\\n4\\n1615 -150 0\\n269 1200 -900\\n-1514 2189 0\\n582 -454 1098\\n\", \"5\\n942 -816 0\\n573 1114 0\\n-800 1001 0\\n250 500 -1\\n-2012 684 0\\n4\\n1615 -150 0\\n181 1200 -900\\n-1514 229 0\\n582 -141 1098\\n\", \"4\\n0 0 0\\n2 0 0\\n2 2 0\\n0 2 0\\n4\\n1 1 -1\\n1 1 1\\n1 3 1\\n1 3 -1\\n\"], \"outputs\": [\"YES\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\"]}", "source": "taco"}
|
Cowboy Beblop is a funny little boy who likes sitting at his computer. He somehow obtained two elastic hoops in the shape of 2D polygons, which are not necessarily convex. Since there's no gravity on his spaceship, the hoops are standing still in the air. Since the hoops are very elastic, Cowboy Beblop can stretch, rotate, translate or shorten their edges as much as he wants.
For both hoops, you are given the number of their vertices, as well as the position of each vertex, defined by the X , Y and Z coordinates. The vertices are given in the order they're connected: the 1st vertex is connected to the 2nd, which is connected to the 3rd, etc., and the last vertex is connected to the first one. Two hoops are connected if it's impossible to pull them to infinity in different directions by manipulating their edges, without having their edges or vertices intersect at any point – just like when two links of a chain are connected. The polygons' edges do not intersect or overlap.
To make things easier, we say that two polygons are well-connected, if the edges of one polygon cross the area of the other polygon in two different directions (from the upper and lower sides of the plane defined by that polygon) a different number of times.
Cowboy Beblop is fascinated with the hoops he has obtained and he would like to know whether they are well-connected or not. Since he’s busy playing with his dog, Zwei, he’d like you to figure it out for him. He promised you some sweets if you help him!
-----Input-----
The first line of input contains an integer n (3 ≤ n ≤ 100 000), which denotes the number of edges of the first polygon. The next N lines each contain the integers x, y and z ( - 1 000 000 ≤ x, y, z ≤ 1 000 000) — coordinates of the vertices, in the manner mentioned above. The next line contains an integer m (3 ≤ m ≤ 100 000) , denoting the number of edges of the second polygon, followed by m lines containing the coordinates of the second polygon’s vertices.
It is guaranteed that both polygons are simple (no self-intersections), and in general that the obtained polygonal lines do not intersect each other. Also, you can assume that no 3 consecutive points of a polygon lie on the same line.
-----Output-----
Your output should contain only one line, with the words "YES" or "NO", depending on whether the two given polygons are well-connected.
-----Example-----
Input
4
0 0 0
2 0 0
2 2 0
0 2 0
4
1 1 -1
1 1 1
1 3 1
1 3 -1
Output
YES
-----Note-----
On the picture below, the two polygons are well-connected, as the edges of the vertical polygon cross the area of the horizontal one exactly once in one direction (for example, from above to below), and zero times in the other (in this case, from below to above). Note that the polygons do not have to be parallel to any of the xy-,xz-,yz- planes in general. [Image]
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"0-(2+3-4+5)\", \"0-(2+3-3+5)\", \"2-(2+3-4+5)\", \"1-(3+2-4+5)\", \"2-(2-3+4+5)\", \"0-(3+4-4+5)\", \"3+(2-4-4+5)\", \"2-(2+2-4+5)\", \"2+(2-4-4+5)\", \"2-(2+2-5+5)\", \"2-(2-3+4+6)\", \"3+(2-4-4+6)\", \"4-(2+5-0+2)\", \"2-(2-3+4+7)\", \"0-(4+5-1+6)\", \"0-(4+5-1+5)\", \"0-(2+3+4-4)\", \"0-(4+2-2+4)\", \"0-(2+3+4-3)\", \"2-(2+5-4+2)\", \"4+(4-4-4+7)\", \"4+(4-2-4+6)\", \"4+(4-2-5+6)\", \"4-(2+3-0+5)\", \"4-(2+4-0+5)\", \"0-(2+4-4+5)\", \"0-(2+3-4+6)\", \"2-(2+4-4+5)\", \"3-(2+4-4+5)\", \"0-(2+3-3+4)\", \"0-(3+3-4+6)\", \"0-(3+3-4+5)\", \"2+(2-4-4+4)\", \"1-(2+4-4+5)\", \"4-(2+2-0+5)\", \"0-(2+4-4+6)\", \"0-(2+3-4+4)\", \"2-(3+2-5+5)\", \"2+(3-4-4+4)\", \"0-(1+4-4+6)\", \"3+(3-4-4+4)\", \"2+(3-3-4+4)\", \"2-(2+3-4+6)\", \"2-(2+4-4+6)\", \"3-(2+4-3+5)\", \"2-(2+3-5+5)\", \"2+(2-5-4+4)\", \"0-(2+2-4+4)\", \"3-(3+4-3+5)\", \"4-(3+3-3+5)\", \"5-(2+4-0+5)\", \"0-(2+2-4+6)\", \"3-(2+3-4+5)\", \"1-(2+2-4+5)\", \"0+(3-3-4+6)\", \"2+(3-4-5+4)\", \"2-(2+2-6+5)\", \"2+(3-4-4+5)\", \"2-(2+5-4+6)\", \"2-(2+4-5+5)\", \"3-(3+4-4+5)\", \"1-(2+2-4+6)\", \"2-(2+2-6+6)\", \"2-(3+5-4+6)\", \"4-(3+3-4+5)\", \"1-(2+2-5+6)\", \"4-(3+3-4+4)\", \"0-(2+2-3+5)\", \"0-(2+3-3+6)\", \"3+(4-4-2+5)\", \"2-(2+4-3+6)\", \"2+(3-4-5+5)\", \"2+(4-4-4+5)\", \"2-(2+5-4+5)\", \"4-(3+3-3+4)\", \"0-(2+2-3+4)\", \"1-(2+4-3+6)\", \"0-(2+4-3+5)\", \"2-(2+5-5+2)\", \"3-(3+0-4+5)\", \"0-(2+4-5+6)\", \"2-(3+1-5+5)\", \"0-(1+5-4+6)\", \"2-(2+3-3+6)\", \"3+(3+4-3-5)\", \"3-(2+3-4+6)\", \"3+(3-4-4+6)\", \"2-(2+4-6+5)\", \"2-(1+5-4+6)\", \"0-(2+3-2+6)\", \"3+(4-5-2+5)\", \"3-(2+4-3+6)\", \"3-(3+1-5+5)\", \"2-(1+3-3+6)\", \"3+(3-4-5+6)\", \"2-(0+5-4+6)\", \"3-(3+1-5+6)\", \"1-(1+3-3+6)\", \"2-(0+5-4+5)\", \"0-(4+4-1+5)\", \"1-(2+3-4+5)\"], \"outputs\": [\"4\\n\", \"3\\n\", \"6\\n\", \"5\\n\", \"12\\n\", \"2\\n\", \"10\\n\", \"7\\n\", \"9\\n\", \"8\\n\", \"13\\n\", \"11\\n\", \"-1\\n\", \"14\\n\", \"-2\\n\", \"-3\\n\", \"-5\\n\", \"0\\n\", \"-4\\n\", \"1\\n\", \"15\\n\", \"16\\n\", \"17\\n\", \"4\\n\", \"3\\n\", \"3\\n\", \"5\\n\", \"5\\n\", \"6\\n\", \"2\\n\", \"4\\n\", \"3\\n\", \"8\\n\", \"4\\n\", \"5\\n\", \"4\\n\", \"3\\n\", \"7\\n\", \"9\\n\", \"5\\n\", \"10\\n\", \"10\\n\", \"7\\n\", \"6\\n\", \"5\\n\", \"7\\n\", \"7\\n\", \"4\\n\", \"4\\n\", \"6\\n\", \"4\\n\", \"6\\n\", \"7\\n\", \"6\\n\", \"10\\n\", \"10\\n\", \"9\\n\", \"10\\n\", \"5\\n\", \"6\\n\", \"5\\n\", \"7\\n\", \"10\\n\", \"4\\n\", \"7\\n\", \"8\\n\", \"6\\n\", \"4\\n\", \"4\\n\", \"10\\n\", \"5\\n\", \"11\\n\", \"11\\n\", \"4\\n\", \"5\\n\", \"3\\n\", \"4\\n\", \"2\\n\", \"2\\n\", \"9\\n\", \"5\\n\", \"8\\n\", \"4\\n\", \"6\\n\", \"12\\n\", \"8\\n\", \"12\\n\", \"7\\n\", \"6\\n\", \"3\\n\", \"9\\n\", \"6\\n\", \"9\\n\", \"7\\n\", \"13\\n\", \"7\\n\", \"10\\n\", \"6\\n\", \"6\\n\", \"-2\\n\", \"5\"]}", "source": "taco"}
|
Tunnel formula
One day while exploring an abandoned mine, you found a long formula S written in the mine. If you like large numbers, you decide to take out the choke and add `(` or `)` so that the result of the formula calculation is as large as possible. If it has to be a mathematical formula even after adding it, how many can it be at the maximum?
There is enough space between the letters, and you can add as many `(` or `)` as you like. If the final formula is a formula, you may write `(` or `)` so that the correspondence of the first parenthesis is broken (see Sample 2). Also, here, <expr> defined by the following BNF is called a mathematical formula. All numbers in the formula are single digits.
<expr> :: = "(" <expr> ")"
| <term> "+" <term>
| <term> "-" <term>
<term> :: = <digit> | <expr>
<digit> :: = "0" | "1" | "2" | "3" | "4"
| "5" | "6" | "7" | "8" | "9"
Constraints
* 3 ≤ | S | ≤ 200
S represents a mathematical formula.
Input Format
Input is given from standard input in the following format.
S
Output Format
Output the answer as an integer.
Sample Input 1
1- (2 + 3-4 + 5)
Sample Output 1
Five
1- (2 + 3- (4 + 5)) is the maximum.
Sample Input 2
1- (2 + 3 + 4)
Sample Output 2
0
(1- (2 + 3) + 4) is the maximum.
Sample Input 3
1- (2 + 3)
Sample Output 3
-Four
Note that 1- (2) + (3) is not the formula here.
Example
Input
1-(2+3-4+5)
Output
5
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[2, 1, 2], [2, 1, 1], [1, 1, 1], [1, 2, 3], [1, 3, 1], [2, 2, 2], [5, 1, 3], [3, 5, 7], [5, 6, 1], [1, 6, 1], [2, 6, 1], [6, 7, 1], [2, 10, 3], [1, 8, 3], [9, 7, 2], [1, 1, 10], [9, 1, 1], [10, 5, 6], [1, 10, 1]], \"outputs\": [[6], [4], [3], [9], [5], [8], [20], [105], [35], [8], [14], [48], [60], [27], [126], [20], [18], [300], [12]]}", "source": "taco"}
|
# Task
* **_Given_** *three integers* `a` ,`b` ,`c`, **_return_** *the **_largest number_** obtained after inserting the following operators and brackets*: `+`, `*`, `()`
* In other words , **_try every combination of a,b,c with [*+()] , and return the Maximum Obtained_**
___
# Consider an Example :
**_With the numbers are 1, 2 and 3_** , *here are some ways of placing signs and brackets*:
* `1 * (2 + 3) = 5`
* `1 * 2 * 3 = 6`
* `1 + 2 * 3 = 7`
* `(1 + 2) * 3 = 9`
So **_the maximum value_** that you can obtain is **_9_**.
___
# Notes
* **_The numbers_** *are always* **_positive_**.
* **_The numbers_** *are in the range* **_(1 ≤ a, b, c ≤ 10)_**.
* *You can use the same operation* **_more than once_**.
* **It's not necessary** *to place all the signs and brackets*.
* **_Repetition_** *in numbers may occur* .
* You **_cannot swap the operands_**. For instance, in the given example **_you cannot get expression_** `(1 + 3) * 2 = 8`.
___
# Input >> Output Examples:
```
expressionsMatter(1,2,3) ==> return 9
```
## **_Explanation_**:
*After placing signs and brackets, the **_Maximum value_** obtained from the expression* `(1+2) * 3 = 9`.
___
```
expressionsMatter(1,1,1) ==> return 3
```
## **_Explanation_**:
*After placing signs, the **_Maximum value_** obtained from the expression is* `1 + 1 + 1 = 3`.
___
```
expressionsMatter(9,1,1) ==> return 18
```
## **_Explanation_**:
*After placing signs and brackets, the **_Maximum value_** obtained from the expression is* `9 * (1+1) = 18`.
___
___
___
# [Playing with Numbers Series](https://www.codewars.com/collections/playing-with-numbers)
# [Playing With Lists/Arrays Series](https://www.codewars.com/collections/playing-with-lists-slash-arrays)
# [Bizarre Sorting-katas](https://www.codewars.com/collections/bizarre-sorting-katas)
# [For More Enjoyable Katas](http://www.codewars.com/users/MrZizoScream/authored)
___
## ALL translations are welcomed
## Enjoy Learning !!
# Zizou
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[\"5\", \"????CIELIS???E?\", \"????CIELISOUR???F\", \"T?KEITE?SY\", \"????????\", \"???C???\"], \"5\\n????CIELIS???E?\\n????CIELISOUR???F\\nT?KEITE?SY\\n????????\\n@??C???\", \"5\\n????CIELIS???E?\\n????CIELISOUR???F\\nYS?ETIEK?T\\n????????\\n@??C???\", \"5\\n????CIELIS???E?\\n????CIELISOUR???F\\nYS?ETIEK?T\\n????>???\\n@??C???\", \"5\\n????CIELI?S??E?\\n????CIELISOUR???F\\nYS?ETIEK?T\\n????>???\\n@??C???\", \"5\\n????CIELI?S??E?\\n????CIELISOUR???F\\nT?KEITE?SY\\n????>???\\n@??C???\", \"5\\n????CIELI?S??E?\\n????CIELISOUR???F\\nT?KEITE?SY\\n????>???\\n@>?C???\", \"5\\n????CIEL??S?IE?\\n????CIELISOUR???F\\nT?KEITE?SY\\n????>???\\n@>?C???\", \"5\\n????CIEL??S?IE?\\n????CIELISOUR??>F\\nT?KEITE?SY\\n????>???\\n@>?C???\", \"5\\n????CIEL??S?IE?\\n????CIELISOUR??>F\\nT?KEITE?SY\\n????>???\\n@>??C??\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nT?KEITE?SY\\n????>???\\n@>??C??\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nT?KEIT?ESY\\n????>???\\n@>??C??\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nT?KEIT?ESY\\n????>???\\n@>??C?>\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nT?KEIT?ESY\\n????>???\\n@>@?C?>\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nT?KEIT?ESY\\n???>????\\n@>@?C?>\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nK?TEIT?ESY\\n???>????\\n@>@?C?>\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nK?TEIT?ESY\\n???>>???\\n@>@?C?>\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nK?TEIT?FSY\\n???>>???\\n@>@?C?>\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nYSF?TIET?K\\n???>>???\\n@>@?C?>\", \"5\\n????CIEL??S?ID?\\n????CIELISOUR??>F\\nYSF?TIET?K\\n???>>???\\n@=@?C?>\", \"5\\n????CIEL??S?ID?\\nF>??RUOSILEIC????\\nYSF?TIET?K\\n???>>???\\n@=@?C?>\", \"5\\n????CIEL??S?ID?\\nF>??RUOSIKEIC????\\nYSF?TIET?K\\n???>>???\\n@=@?C?>\", \"5\\n????CIEL??S?ID?\\nF>??RUOSIKEIC????\\nYSF?TIFT?K\\n???>>???\\n@=@?C?>\", \"5\\n????CIEL??S?ID?\\nF>??RUOSIKEIC????\\nK?TFIT?FSY\\n???>>???\\n@=@?C?>\", \"5\\n??@?CIEL??S?ID?\\nF>??RUOSIKEIC????\\nK?TFIT?FSY\\n???>>???\\n@=@?C?>\", \"5\\n??@?CIEL??S?ID?\\nF>??RUOSIKEIC????\\nK?TFIT?FSX\\n???>>???\\n@=@?C?>\", \"5\\n??@?CIEL??S?ID?\\nF>??RUOSIKEIC????\\nK?TFIT?FSX\\n???>>???\\n@=@?B?>\", \"5\\nI?@?C?EL??S?ID?\\nF>??RUOSIKEIC????\\nK?TFIT?FSX\\n???>>???\\n@=@?B?>\", \"5\\nI?@?C?EL??S?ID?\\nF>??RUOSIKEIC????\\nK?TFIT?FSX\\n@??>>???\\n@=@?B?>\", \"5\\nI?@?C?EL??S?ID?\\nF>??RUOSIKEIC????\\nK?TFIT?FSX\\n@??>>???\\n>?B?@=@\", \"5\\nI?@?C?EL??S?ID?\\nF>??RUORIKEIC????\\nK?TFIT?FSX\\n@??>>???\\n>?B?@=@\", \"5\\nI?@???EL??S?IDC\\nF>??RUORIKEIC????\\nK?TFIT?FSX\\n@??>>???\\n>?B?@=@\", \"5\\nI?@???EL??S?IDC\\nF>??RUORIKEIC????\\nK?TEIT?FSX\\n@??>>???\\n>?B?@=@\", \"5\\nI?@???EL??S?IDC\\nF>??RUORIKEIC????\\nK?TEIT?FSX\\n@??>>???\\n>?B??=@\", \"5\\nI?@???EL??S?IDC\\nF>??QUORIKEIC????\\nK?TEIT?FSX\\n@??>>???\\n>?B??=@\", \"5\\nI?@???EL??S?IDC\\nF>??QUORIKEIC????\\nK?TEIT?FSX\\n@??>>???\\n??B?>=@\", \"5\\nI@@???EL??S?IDC\\nF>??QUORIKEIC????\\nK?TEIT?FSX\\n@??>>???\\n??B?>=@\", \"5\\nI@@???EL??S?IDC\\nF>??QUORIKEIC????\\nK?TEIT?FSX\\n@??>???>\\n??B?>=@\", \"5\\nI@@???EL??S?IDC\\nF>??QUORIKEIC????\\nK?TEIT?FSX\\n@??????>\\n??B?>=@\", \"5\\nI@@???EL??S?IDC\\nF>??QUORIKEIC????\\nXSF?TIET?K\\n@??????>\\n??B?>=@\", \"5\\nI@@???EL??S?IDC\\nF>??QUORIKEIC????\\nXSF?TIET?J\\n@??????>\\n??B?>=@\", \"5\\nI@@???EL??S?IDC\\nF>??QUORIKEIC????\\nXSF?TIET?J\\n@??????>\\n??B?>>@\", \"5\\nH@@???EL??S?IDC\\nF>??QUORIKEIC????\\nXSF?TIET?J\\n@??????>\\n??B?>>@\", \"5\\nI@@???EL??S?IDC\\nF>??QUORIKEIC????\\nXSF?TIET?J\\n@??????>\\n@>>?B??\", \"5\\nCDI?S??LE???@@I\\nF>??QUORIKEIC????\\nXSF?TIET?J\\n@??????>\\n@>>?B??\", \"5\\nCDI?S??LE???@@I\\nF>??QUORIKEIC????\\nXSF?TIET?J\\nA??????>\\n@>>?B??\", \"5\\nCDI?S??LE???@@I\\nF>??QUORHKEIC????\\nXSF?TIET?J\\nA??????>\\n@>>?B??\", \"5\\nCDI?S??LE???@@I\\nF>??QUORHKE?CI???\\nXSF?TIET?J\\nA??????>\\n@>>?B??\", \"5\\nCDI?S??LE???@@I\\nU>??QFORHKE?CI???\\nXSF?TIET?J\\nA??????>\\n@>>?B??\", \"5\\nCDI?S??LE???@@I\\n???IC?EKHROFQ??>U\\nXSF?TIET?J\\nA??????>\\n@>>?B??\", \"5\\nCDI?S??LE???@@I\\n???IC?EKHROFQ??>U\\nXSF?TIET?J\\nA?????>>\\n@>>?B??\", \"5\\nCDI?S??LE???@@I\\n???IC?EKHROFQ??>U\\nXSF?TIET?J\\nA?????>>\\n@=>?B??\", \"5\\nCDI?S??LD???@@I\\n???IC?EKHROFQ??>U\\nXSF?TIET?J\\nA?????>>\\n@=>?B??\", \"5\\nCDJ?S??LD???@@I\\n???IC?EKHROFQ??>U\\nXSF?TIET?J\\nA?????>>\\n@=>?B??\", \"5\\nCDJ?S??LD???@@I\\n???IC?EKHQOFQ??>U\\nXSF?TIET?J\\nA?????>>\\n@=>?B??\", \"5\\nCDJ?S??LD???@@I\\nU>??QFOQHKE?CI???\\nXSF?TIET?J\\nA?????>>\\n@=>?B??\", \"5\\nCDJ?S??LD???@@I\\nU>??QFOQHKE?CI???\\nXSF?TIET?J\\nA????@>>\\n@=>?B??\", \"5\\nCDJ?S??LD???@@I\\nU???QFOQHKE?CI?>?\\nXSF?TIET?J\\nA????@>>\\n@=>?B??\", \"5\\nCD??S??LD??J@@I\\nU???QFOQHKE?CI?>?\\nXSF?TIET?J\\nA????@>>\\n@=>?B??\", \"5\\nCD??S??LD??J@@I\\nU???QFOQHKE?CI?>?\\nXSF?TIET?J\\nA????@=>\\n@=>?B??\", \"5\\nCD?@S??LD??J@@I\\nU???QFOQHKE?CI?>?\\nXSF?TIET?J\\nA????@=>\\n@=>?B??\", \"5\\nCD?@S??LD??J@@I\\nU???QFOQHKE?CI?>?\\nXSF?TIET?J\\nA????@=>\\n@=>?C??\", \"5\\nCD?@S??LD??J@@I\\nU???QFOQHKE?CI?>?\\nXSF?TIET?J\\n>=@????A\\n@=>?C??\", \"5\\nCD?@S??LD??J@@I\\nU???QFOQHKE?CI?>?\\nJ?TEIT?FSX\\n>=@????A\\n@=>?C??\", \"5\\nI@@J??DL??S@?DC\\nU???QFOQHKE?CI?>?\\nJ?TEIT?FSX\\n>=@????A\\n@=>?C??\", \"5\\nI@@J??DL??S@?DC\\nU???QFOQGKE?CI?>?\\nJ?TEIT?FSX\\n>=@????A\\n@=>?C??\", \"5\\nI@@J??DL??S@?DC\\nU???QFOQGKE?CI?>?\\nJ?TEHT?FSX\\n>=@????A\\n@=>?C??\", \"5\\nI@@J??DL??S@?DC\\nU???QFOQGKE?CI?>?\\nJ?TEHT?FSX\\n>=@????A\\n??C?>=@\", \"5\\nI@@J??DL??S@?DC\\n?>?IC?EKGQOFQ???U\\nJ?TEHT?FSX\\n>=@????A\\n??C?>=@\", \"5\\nI@@J??DL??S@?DC\\n?>?IC?EKGQOFQ???U\\nJ?TEHT?FSX\\n>=@????A\\n??C??=@\", \"5\\nI@AJ??DL??S@?DC\\n?>?IC?EKGQOFQ???U\\nJ?TEHT?FSX\\n>=@????A\\n??C??=@\", \"5\\nI@AJ??DL??S@?DC\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSX\\n>=@????A\\n??C??=@\", \"5\\nI@AJ??DL??S@?DC\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSX\\n>=@?@??A\\n??C??=@\", \"5\\nI@AJ??DL??S@?DC\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSY\\n>=@?@??A\\n??C??=@\", \"5\\nI@AJ??DL??S@?DC\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSY\\n>=@?@??A\\n??C??<@\", \"5\\nCD?@S??LD??JA@I\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSY\\n>=@?@??A\\n??C??<@\", \"5\\nCD?@S??LD??JA@I\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSY\\n>=@?@??A\\n??B??<@\", \"5\\nCD@@S??LD??JA@I\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSY\\n>=@?@??A\\n??B??<@\", \"5\\nCD@@S??LD??JA@I\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSY\\n>=@?@??A\\n??A??<@\", \"5\\nCD@@S??LD??JA@I\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSX\\n>=@?@??A\\n??A??<@\", \"5\\nCD@@S??LD??JA@I\\n?>?IC?EKGQOFR???U\\nJ?TFHT?FSX\\n>=@?@??A\\n??A??<@\", \"5\\nCD@@S??LD??JA@I\\n?>?IC?EKGQOFR???U\\nJ?TFHT?FSX\\n>=@?@@?A\\n??A??<@\", \"5\\nCD@@S??LD??JA@I\\n?>?IC?EKGQOFR???U\\nJ?TFHT?FSX\\n>=@@@@??\\n??A??<@\", \"5\\nCD@@S??LD??JA@I\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSX\\n>=@@@@??\\n??A??<@\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSX\\n>=@@@@??\\n??A??<@\", \"5\\nI@AJ??DL??S@@EC\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSX\\n>=@@@@??\\n??A??<@\", \"5\\nI@AJ??DL??S@@EC\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSX\\n??@@@@=>\\n??A??<@\", \"5\\nI@AJ??DL??S@@EC\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSX\\n??@@@@=>\\n@<??A??\", \"5\\nI@AJ??DL??S@@EC\\n?>?IC?EKGQOFQ???U\\nJ?TFHT?FSX\\n??@@@@=>\\n@A??<??\", \"5\\nI@AJ??DL??S@@EC\\n?>?IC?EOGQKFQ???U\\nJ?TFHT?FSX\\n??@@@@=>\\n@A??<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EOGQKFQ???U\\nJ?TFHT?FSX\\n??@@@@=>\\n@A??<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EOGQKFQ???U\\nXSF?THFT?J\\n??@@@@=>\\n@A??<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EOGQKFQ???U\\nXSF?THFT?J\\n?=@@@@?>\\n@A??<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EOGQKFQ???U\\nJ?TFHT?FSX\\n?=@@@@?>\\n@A??<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EOGQKFQ???U\\nJ?TFST?FHX\\n?=@@@@?>\\n@A??<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EOGQKFQ???U\\nJ?TFST?FHX\\n?=@@@@?>\\n@A>?<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EPGQKFQ???U\\nJ?TFST?FHX\\n?=@@@@?>\\n@A>?<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EPGQKFQ???U\\nJ?TFST?FHX\\n>?@@@@=?\\n@A>?<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EPGRKFQ???U\\nJ?TFST?FHX\\n>?@@@@=?\\n@A>?<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EPGRKFQ??>U\\nJ?TFST?FHX\\n>?@@@@=?\\n@A>?<??\", \"5\\nCE@@S??LD??JA@I\\n?>?IC?EPGRKFQ??>U\\nXHF?TSFT?J\\n>?@@@@=?\\n@A>?<??\", \"5\\n????CIELIS???E?\\n????CIELISOUR???F\\nT?KEITE?SY\\n????????\\n???C???\"], \"outputs\": [[\"CHEFCIELISACHEF\", \"CHEFCIELISOURCHEF\", \"TAKEITEASY\", \"CHEFCHEF\", \"AAACHEF\"], \"CHEFCIELISACHEF\\nCHEFCIELISOURCHEF\\nTAKEITEASY\\nCHEFCHEF\\n@AACHEF\\n\", \"CHEFCIELISACHEF\\nCHEFCIELISOURCHEF\\nYSAETIEKAT\\nCHEFCHEF\\n@AACHEF\\n\", \"CHEFCIELISACHEF\\nCHEFCIELISOURCHEF\\nYSAETIEKAT\\nCHEF>AAA\\n@AACHEF\\n\", \"CHEFCIELIASCHEF\\nCHEFCIELISOURCHEF\\nYSAETIEKAT\\nCHEF>AAA\\n@AACHEF\\n\", \"CHEFCIELIASCHEF\\nCHEFCIELISOURCHEF\\nTAKEITEASY\\nCHEF>AAA\\n@AACHEF\\n\", \"CHEFCIELIASCHEF\\nCHEFCIELISOURCHEF\\nTAKEITEASY\\nCHEF>AAA\\n@>ACHEF\\n\", \"CHEFCIELAASAIEA\\nCHEFCIELISOURCHEF\\nTAKEITEASY\\nCHEF>AAA\\n@>ACHEF\\n\", \"CHEFCIELAASAIEA\\nCHEFCIELISOURAA>F\\nTAKEITEASY\\nCHEF>AAA\\n@>ACHEF\\n\", \"CHEFCIELAASAIEA\\nCHEFCIELISOURAA>F\\nTAKEITEASY\\nCHEF>AAA\\n@>AACAA\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nTAKEITEASY\\nCHEF>AAA\\n@>AACAA\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nTAKEITAESY\\nCHEF>AAA\\n@>AACAA\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nTAKEITAESY\\nCHEF>AAA\\n@>AACA>\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nTAKEITAESY\\nCHEF>AAA\\n@>@ACA>\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nTAKEITAESY\\nAAA>CHEF\\n@>@ACA>\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nKATEITAESY\\nAAA>CHEF\\n@>@ACA>\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nKATEITAESY\\nAAA>>AAA\\n@>@ACA>\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nKATEITAFSY\\nAAA>>AAA\\n@>@ACA>\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nYSFATIETAK\\nAAA>>AAA\\n@>@ACA>\\n\", \"CHEFCIELAASAIDA\\nCHEFCIELISOURAA>F\\nYSFATIETAK\\nAAA>>AAA\\n@=@ACA>\\n\", \"CHEFCIELAASAIDA\\nF>AARUOSILEICCHEF\\nYSFATIETAK\\nAAA>>AAA\\n@=@ACA>\\n\", \"CHEFCIELAASAIDA\\nF>AARUOSIKEICCHEF\\nYSFATIETAK\\nAAA>>AAA\\n@=@ACA>\\n\", \"CHEFCIELAASAIDA\\nF>AARUOSIKEICCHEF\\nYSFATIFTAK\\nAAA>>AAA\\n@=@ACA>\\n\", \"CHEFCIELAASAIDA\\nF>AARUOSIKEICCHEF\\nKATFITAFSY\\nAAA>>AAA\\n@=@ACA>\\n\", \"AA@ACIELAASAIDA\\nF>AARUOSIKEICCHEF\\nKATFITAFSY\\nAAA>>AAA\\n@=@ACA>\\n\", \"AA@ACIELAASAIDA\\nF>AARUOSIKEICCHEF\\nKATFITAFSX\\nAAA>>AAA\\n@=@ACA>\\n\", \"AA@ACIELAASAIDA\\nF>AARUOSIKEICCHEF\\nKATFITAFSX\\nAAA>>AAA\\n@=@ABA>\\n\", \"IA@ACAELAASAIDA\\nF>AARUOSIKEICCHEF\\nKATFITAFSX\\nAAA>>AAA\\n@=@ABA>\\n\", \"IA@ACAELAASAIDA\\nF>AARUOSIKEICCHEF\\nKATFITAFSX\\n@AA>>AAA\\n@=@ABA>\\n\", \"IA@ACAELAASAIDA\\nF>AARUOSIKEICCHEF\\nKATFITAFSX\\n@AA>>AAA\\n>ABA@=@\\n\", \"IA@ACAELAASAIDA\\nF>AARUORIKEICCHEF\\nKATFITAFSX\\n@AA>>AAA\\n>ABA@=@\\n\", \"IA@AAAELAASAIDC\\nF>AARUORIKEICCHEF\\nKATFITAFSX\\n@AA>>AAA\\n>ABA@=@\\n\", \"IA@AAAELAASAIDC\\nF>AARUORIKEICCHEF\\nKATEITAFSX\\n@AA>>AAA\\n>ABA@=@\\n\", \"IA@AAAELAASAIDC\\nF>AARUORIKEICCHEF\\nKATEITAFSX\\n@AA>>AAA\\n>ABAA=@\\n\", \"IA@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nKATEITAFSX\\n@AA>>AAA\\n>ABAA=@\\n\", \"IA@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nKATEITAFSX\\n@AA>>AAA\\nAABA>=@\\n\", \"I@@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nKATEITAFSX\\n@AA>>AAA\\nAABA>=@\\n\", \"I@@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nKATEITAFSX\\n@AA>AAA>\\nAABA>=@\\n\", \"I@@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nKATEITAFSX\\n@AACHEF>\\nAABA>=@\\n\", \"I@@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nXSFATIETAK\\n@AACHEF>\\nAABA>=@\\n\", \"I@@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nXSFATIETAJ\\n@AACHEF>\\nAABA>=@\\n\", \"I@@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nXSFATIETAJ\\n@AACHEF>\\nAABA>>@\\n\", \"H@@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nXSFATIETAJ\\n@AACHEF>\\nAABA>>@\\n\", \"I@@AAAELAASAIDC\\nF>AAQUORIKEICCHEF\\nXSFATIETAJ\\n@AACHEF>\\n@>>ABAA\\n\", \"CDIASAALEAAA@@I\\nF>AAQUORIKEICCHEF\\nXSFATIETAJ\\n@AACHEF>\\n@>>ABAA\\n\", \"CDIASAALEAAA@@I\\nF>AAQUORIKEICCHEF\\nXSFATIETAJ\\nAAACHEF>\\n@>>ABAA\\n\", \"CDIASAALEAAA@@I\\nF>AAQUORHKEICCHEF\\nXSFATIETAJ\\nAAACHEF>\\n@>>ABAA\\n\", \"CDIASAALEAAA@@I\\nF>AAQUORHKEACIAAA\\nXSFATIETAJ\\nAAACHEF>\\n@>>ABAA\\n\", \"CDIASAALEAAA@@I\\nU>AAQFORHKEACIAAA\\nXSFATIETAJ\\nAAACHEF>\\n@>>ABAA\\n\", \"CDIASAALEAAA@@I\\nAAAICAEKHROFQAA>U\\nXSFATIETAJ\\nAAACHEF>\\n@>>ABAA\\n\", \"CDIASAALEAAA@@I\\nAAAICAEKHROFQAA>U\\nXSFATIETAJ\\nAACHEF>>\\n@>>ABAA\\n\", \"CDIASAALEAAA@@I\\nAAAICAEKHROFQAA>U\\nXSFATIETAJ\\nAACHEF>>\\n@=>ABAA\\n\", \"CDIASAALDAAA@@I\\nAAAICAEKHROFQAA>U\\nXSFATIETAJ\\nAACHEF>>\\n@=>ABAA\\n\", \"CDJASAALDAAA@@I\\nAAAICAEKHROFQAA>U\\nXSFATIETAJ\\nAACHEF>>\\n@=>ABAA\\n\", \"CDJASAALDAAA@@I\\nAAAICAEKHQOFQAA>U\\nXSFATIETAJ\\nAACHEF>>\\n@=>ABAA\\n\", \"CDJASAALDAAA@@I\\nU>AAQFOQHKEACIAAA\\nXSFATIETAJ\\nAACHEF>>\\n@=>ABAA\\n\", \"CDJASAALDAAA@@I\\nU>AAQFOQHKEACIAAA\\nXSFATIETAJ\\nACHEF@>>\\n@=>ABAA\\n\", \"CDJASAALDAAA@@I\\nUAAAQFOQHKEACIA>A\\nXSFATIETAJ\\nACHEF@>>\\n@=>ABAA\\n\", \"CDAASAALDAAJ@@I\\nUAAAQFOQHKEACIA>A\\nXSFATIETAJ\\nACHEF@>>\\n@=>ABAA\\n\", \"CDAASAALDAAJ@@I\\nUAAAQFOQHKEACIA>A\\nXSFATIETAJ\\nACHEF@=>\\n@=>ABAA\\n\", \"CDA@SAALDAAJ@@I\\nUAAAQFOQHKEACIA>A\\nXSFATIETAJ\\nACHEF@=>\\n@=>ABAA\\n\", \"CDA@SAALDAAJ@@I\\nUAAAQFOQHKEACIA>A\\nXSFATIETAJ\\nACHEF@=>\\n@=>ACAA\\n\", \"CDA@SAALDAAJ@@I\\nUAAAQFOQHKEACIA>A\\nXSFATIETAJ\\n>=@CHEFA\\n@=>ACAA\\n\", \"CDA@SAALDAAJ@@I\\nUAAAQFOQHKEACIA>A\\nJATEITAFSX\\n>=@CHEFA\\n@=>ACAA\\n\", \"I@@JAADLAAS@ADC\\nUAAAQFOQHKEACIA>A\\nJATEITAFSX\\n>=@CHEFA\\n@=>ACAA\\n\", \"I@@JAADLAAS@ADC\\nUAAAQFOQGKEACIA>A\\nJATEITAFSX\\n>=@CHEFA\\n@=>ACAA\\n\", \"I@@JAADLAAS@ADC\\nUAAAQFOQGKEACIA>A\\nJATEHTAFSX\\n>=@CHEFA\\n@=>ACAA\\n\", \"I@@JAADLAAS@ADC\\nUAAAQFOQGKEACIA>A\\nJATEHTAFSX\\n>=@CHEFA\\nAACA>=@\\n\", \"I@@JAADLAAS@ADC\\nA>AICAEKGQOFQAAAU\\nJATEHTAFSX\\n>=@CHEFA\\nAACA>=@\\n\", \"I@@JAADLAAS@ADC\\nA>AICAEKGQOFQAAAU\\nJATEHTAFSX\\n>=@CHEFA\\nAACAA=@\\n\", \"I@AJAADLAAS@ADC\\nA>AICAEKGQOFQAAAU\\nJATEHTAFSX\\n>=@CHEFA\\nAACAA=@\\n\", \"I@AJAADLAAS@ADC\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSX\\n>=@CHEFA\\nAACAA=@\\n\", \"I@AJAADLAAS@ADC\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSX\\n>=@A@AAA\\nAACAA=@\\n\", \"I@AJAADLAAS@ADC\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSY\\n>=@A@AAA\\nAACAA=@\\n\", \"I@AJAADLAAS@ADC\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSY\\n>=@A@AAA\\nAACAA<@\\n\", \"CDA@SAALDAAJA@I\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSY\\n>=@A@AAA\\nAACAA<@\\n\", \"CDA@SAALDAAJA@I\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSY\\n>=@A@AAA\\nAABAA<@\\n\", \"CD@@SAALDAAJA@I\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSY\\n>=@A@AAA\\nAABAA<@\\n\", \"CD@@SAALDAAJA@I\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSY\\n>=@A@AAA\\nAAAAA<@\\n\", \"CD@@SAALDAAJA@I\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSX\\n>=@A@AAA\\nAAAAA<@\\n\", \"CD@@SAALDAAJA@I\\nA>AICAEKGQOFRAAAU\\nJATFHTAFSX\\n>=@A@AAA\\nAAAAA<@\\n\", \"CD@@SAALDAAJA@I\\nA>AICAEKGQOFRAAAU\\nJATFHTAFSX\\n>=@A@@AA\\nAAAAA<@\\n\", \"CD@@SAALDAAJA@I\\nA>AICAEKGQOFRAAAU\\nJATFHTAFSX\\n>=@@@@AA\\nAAAAA<@\\n\", \"CD@@SAALDAAJA@I\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSX\\n>=@@@@AA\\nAAAAA<@\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSX\\n>=@@@@AA\\nAAAAA<@\\n\", \"I@AJAADLAAS@@EC\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSX\\n>=@@@@AA\\nAAAAA<@\\n\", \"I@AJAADLAAS@@EC\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSX\\nAA@@@@=>\\nAAAAA<@\\n\", \"I@AJAADLAAS@@EC\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSX\\nAA@@@@=>\\n@<AAAAA\\n\", \"I@AJAADLAAS@@EC\\nA>AICAEKGQOFQAAAU\\nJATFHTAFSX\\nAA@@@@=>\\n@AAA<AA\\n\", \"I@AJAADLAAS@@EC\\nA>AICAEOGQKFQAAAU\\nJATFHTAFSX\\nAA@@@@=>\\n@AAA<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEOGQKFQAAAU\\nJATFHTAFSX\\nAA@@@@=>\\n@AAA<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEOGQKFQAAAU\\nXSFATHFTAJ\\nAA@@@@=>\\n@AAA<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEOGQKFQAAAU\\nXSFATHFTAJ\\nA=@@@@A>\\n@AAA<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEOGQKFQAAAU\\nJATFHTAFSX\\nA=@@@@A>\\n@AAA<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEOGQKFQAAAU\\nJATFSTAFHX\\nA=@@@@A>\\n@AAA<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEOGQKFQAAAU\\nJATFSTAFHX\\nA=@@@@A>\\n@A>A<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEPGQKFQAAAU\\nJATFSTAFHX\\nA=@@@@A>\\n@A>A<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEPGQKFQAAAU\\nJATFSTAFHX\\n>A@@@@=A\\n@A>A<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEPGRKFQAAAU\\nJATFSTAFHX\\n>A@@@@=A\\n@A>A<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEPGRKFQAA>U\\nJATFSTAFHX\\n>A@@@@=A\\n@A>A<AA\\n\", \"CE@@SAALDAAJA@I\\nA>AICAEPGRKFQAA>U\\nXHFATSFTAJ\\n>A@@@@=A\\n@A>A<AA\\n\", \"CHEFCIELISACHEF\\nCHEFCIELISOURCHEF\\nTAKEITEASY\\nCHEFCHEF\\nAAACHEF\\n\"]}", "source": "taco"}
|
Chef Ciel wants to put a fancy neon signboard over the entrance of her restaurant. She has not enough money to buy the new one so she bought some old neon signboard through the internet. Ciel was quite disappointed when she received her order - some of its letters were broken. But she realized that this is even better - she could replace each broken letter by any letter she wants. So she decided to do such a replacement that the resulting signboard will contain the word "CHEF" as many times as possible.
We can model the signboard as a string S having capital letters from 'A' to 'Z', inclusive, and question marks '?'. Letters in the string indicate the intact letters at the signboard, while question marks indicate broken letters. So Ciel will replace each question mark with some capital letter and her goal is to get the string that contains as many substrings equal to "CHEF" as possible. If there exist several such strings, she will choose the lexicographically smallest one.
Note 1. The string S = S1...SN has the substring "CHEF" if for some i we have SiSi+1Si+2Si+3 = "CHEF". The number of times "CHEF" is the substring of S is the number of those i for which SiSi+1Si+2Si+3 = "CHEF".
Note 2. The string A = A1...AN is called lexicographically smaller than the string B = B1...BN if there exists K from 1 to N, inclusive, such that Ai = Bi for i = 1, ..., K-1, and AK < BK. In particular, A is lexicographically smaller than B if A1 < B1. We compare capital letters by their positions in the English alphabet. So 'A' is the smallest letter, 'B' is the second smallest letter, ..., 'Z' is the largest letter.
-----Input-----
The first line of the input contains an integer T denoting the number of test cases. The description of T test cases follows. The only line of each test case contains a string S.
-----Output-----
For each test case, output a single line containing the content of the signboard Chef Ciel will come up with. That is you should output the lexicographically smallest string that could be obtained from the input string by replacing all its question marks by some capital letters and having as many substrings equal to "CHEF" as possible.
-----Constraints-----
- 1 ≤ T ≤ 2013
- 1 ≤ length of S ≤ 2013
- Each character in S is either a capital letter from 'A' to 'Z', inclusive, or the question mark '?'.
-----Example-----
Input:
5
????CIELIS???E?
????CIELISOUR???F
T?KEITE?SY
????????
???C???
Output:
CHEFCIELISACHEF
CHEFCIELISOURCHEF
TAKEITEASY
CHEFCHEF
AAACHEF
-----Explanation -----
Example Case 1. Here the resulting string can have at most 2 substrings equal to "CHEF". For example, some possible such strings are:
- CHEFCIELISACHEF
- CHEFCIELISQCHEF
- CHEFCIELISZCHEF
However, lexicographically smallest one is the first one.
Example Case 3. Here the resulting string cannot have "CHEF" as its substring. Therefore, you must simply output the lexicographically smallest string that can be obtained from the given one by replacing question marks with capital letters.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"10\\n1598114589\", \"11\\n18396312558\", \"10\\n2555486547\", \"10\\n2722382398\", \"10\\n2713182985\", \"10\\n4333783596\", \"11\\n24764186449\", \"10\\n1859787539\", \"10\\n1888971773\", \"10\\n6843843631\", \"10\\n3639938767\", \"10\\n3398916166\", \"11\\n31342613688\", \"10\\n1138256531\", \"10\\n6311722321\", \"10\\n2146117495\", \"11\\n11732659512\", \"10\\n8393399249\", \"11\\n21747269818\", \"10\\n1152629286\", \"10\\n1687456833\", \"10\\n6342787912\", \"10\\n6491221359\", \"10\\n1495572657\", \"11\\n46236447879\", \"10\\n1384922354\", \"10\\n7133793268\", \"11\\n69985758395\", \"10\\n1533436389\", \"11\\n37563282717\", \"11\\n13573893934\", \"10\\n5426322888\", \"10\\n6761648247\", \"10\\n1985693477\", \"10\\n3984183885\", \"11\\n16235894463\", \"11\\n71389826121\", \"11\\n11453821354\", \"10\\n3543684464\", \"10\\n1544736988\", \"11\\n24886231412\", \"11\\n34412849886\", \"10\\n1273282833\", \"11\\n12313792224\", \"11\\n51515413842\", \"10\\n11468715970\", \"10\\n12522486885\", \"11\\n19179648972\", \"10\\n1726634825\", \"11\\n53354715551\", \"10\\n5416366896\", \"11\\n29864492875\", \"10\\n2395828814\", \"10\\n2119337566\", \"10\\n3459689681\", \"11\\n32977715929\", \"10\\n3267662441\", \"11\\n76469488291\", \"10\\n1769895679\", \"10\\n2821537972\", \"10\\n3815374889\", \"10\\n2524469986\", \"10\\n1411794715\", \"11\\n49751385358\", \"11\\n45699867216\", \"10\\n1945494674\", \"11\\n51465697558\", \"11\\n36995491458\", \"10\\n1331864417\", \"10\\n2862593112\", \"10\\n4567164252\", \"10\\n6694162379\", \"11\\n21552229582\", \"10\\n5737111899\", \"10\\n1883894335\", \"10\\n2819875386\", \"11\\n85958136119\", \"10\\n9652738844\", \"11\\n17192962318\", \"10\\n7875574934\", \"11\\n129483884450\", \"10\\n2672272864\", \"11\\n15785446682\", \"11\\n14172787225\", \"11\\n54934439819\", \"10\\n4575545526\", \"11\\n128935478480\", \"10\\n1879126279\", \"10\\n5548446534\", \"10\\n1792946849\", \"10\\n6163557937\", \"10\\n1885251813\", \"10\\n3446732954\", \"11\\n99578195397\", \"10\\n4845296427\", \"11\\n25786792429\", \"10\\n1757558463\", \"10\\n2479654495\", \"10\\n2383371798\", \"10\\n2353583592\", \"10\\n1236547896\", \"11\\n31415926535\"], \"outputs\": [\"142\\n853\\n967\\n\", \"124\\n857\\n369\\n\", \"123\\n659\\n847\\n\", \"139\\n428\\n576\\n\", \"317\\n482\\n659\\n\", \"124\\n783\\n695\\n\", \"318\\n246\\n597\\n\", \"124\\n853\\n796\\n\", \"173\\n892\\n456\\n\", \"125\\n347\\n689\\n\", \"124\\n567\\n938\\n\", \"162\\n934\\n857\\n\", \"134\\n562\\n789\\n\", \"138\\n452\\n769\\n\", \"136\\n724\\n589\\n\", \"216\\n374\\n859\\n\", \"326\\n715\\n489\\n\", \"124\\n395\\n867\\n\", \"174\\n823\\n965\\n\", \"134\\n526\\n798\\n\", \"129\\n654\\n837\\n\", \"124\\n973\\n586\\n\", \"213\\n495\\n678\\n\", \"138\\n462\\n957\\n\", \"123\\n546\\n879\\n\", \"135\\n684\\n729\\n\", \"132\\n796\\n458\\n\", \"124\\n396\\n857\\n\", \"142\\n536\\n789\\n\", \"128\\n734\\n569\\n\", \"215\\n437\\n698\\n\", \"135\\n624\\n789\\n\", \"123\\n645\\n789\\n\", \"134\\n697\\n582\\n\", \"126\\n483\\n759\\n\", \"127\\n635\\n498\\n\", \"317\\n824\\n965\\n\", \"214\\n835\\n679\\n\", \"127\\n359\\n648\\n\", \"152\\n748\\n369\\n\", \"135\\n427\\n869\\n\", \"125\\n486\\n397\\n\", \"127\\n483\\n569\\n\", \"137\\n429\\n568\\n\", \"248\\n513\\n679\\n\", \"215\\n479\\n683\\n\", \"124\\n358\\n796\\n\", \"213\\n796\\n584\\n\", \"153\\n726\\n984\\n\", \"153\\n742\\n689\\n\", \"145\\n632\\n897\\n\", \"123\\n495\\n687\\n\", \"146\\n823\\n579\\n\", \"124\\n936\\n875\\n\", \"123\\n854\\n697\\n\", \"153\\n792\\n468\\n\", \"135\\n426\\n897\\n\", \"135\\n946\\n287\\n\", \"123\\n798\\n654\\n\", \"124\\n586\\n379\\n\", \"215\\n983\\n647\\n\", \"124\\n356\\n789\\n\", \"235\\n641\\n897\\n\", \"132\\n458\\n976\\n\", \"213\\n765\\n894\\n\", \"123\\n945\\n678\\n\", \"214\\n856\\n379\\n\", \"142\\n958\\n637\\n\", \"235\\n417\\n689\\n\", \"124\\n368\\n957\\n\", \"138\\n764\\n952\\n\", \"145\\n692\\n873\\n\", \"123\\n458\\n697\\n\", \"173\\n852\\n946\\n\", \"126\\n835\\n947\\n\", \"124\\n983\\n675\\n\", \"234\\n618\\n795\\n\", \"125\\n376\\n849\\n\", \"234\\n917\\n685\\n\", \"123\\n574\\n689\\n\", \"125\\n694\\n738\\n\", \"127\\n386\\n594\\n\", \"123\\n587\\n469\\n\", \"143\\n725\\n869\\n\", \"125\\n934\\n867\\n\", \"126\\n354\\n879\\n\", \"123\\n689\\n745\\n\", \"126\\n873\\n495\\n\", \"127\\n348\\n569\\n\", \"123\\n794\\n568\\n\", \"124\\n635\\n897\\n\", \"134\\n852\\n679\\n\", \"128\\n739\\n645\\n\", \"182\\n974\\n356\\n\", \"153\\n648\\n927\\n\", \"134\\n652\\n879\\n\", \"123\\n746\\n589\\n\", \"123\\n547\\n698\\n\", \"124\\n735\\n986\\n\", \"123\\n495\\n678\\n\", \"123\\n456\\n789\", \"137\\n456\\n892\"]}", "source": "taco"}
|
Problem
Den, the phone number of Ukunikia Co., Ltd., enters a very long phone number into the phone every day.
One day, too tired, Den came up with a surprising idea.
"Isn't it even a little easier if you rearrange the arrangement of the buttons on the phone ?!"
The phone has squares evenly spaced at $ 3 \ times 3 $, and each of the nine squares has one button from 1 to 9 that can be sorted.
When typing a phone number, Den can do two things with just one hand:
* Move your index finger to touch one of the adjacent buttons on the side of the button you are currently touching.
* Press the button that your index finger is touching.
Initially, the index finger can be placed to touch any of the buttons 1-9.
Mr. Den thinks that the arrangement that can minimize the number of movements of the index finger from pressing the first button to the end of pressing the last button is efficient.
Now, here is the phone number of the customer with a length of $ N $.
What kind of arrangement is most efficient when considering only the customer's phone number?
Make the arrangement by rearranging the buttons.
Constraints
The input satisfies the following conditions.
* $ 1 \ leq N \ leq 10 ^ 5 $
* $ S $ is a string consisting of any number from 1 to 9.
Input
The input is given in the following format.
$ N $
$ S $
The first line gives the customer's phone number length $ N $.
The customer's phone number is given to the first line on the second line.
Output
Output the most efficient placement with no blanks on the 3 lines.
However, if there are multiple possible answers, start from the upper left frame.
one two Three
456
789
When arranging the numbers in the order of, output the one that is the smallest in the dictionary order.
Examples
Input
10
1236547896
Output
123
456
789
Input
11
31415926535
Output
137
456
892
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3 3 2\\n1 2\\n2 1\\n3 3\\n3 2\\n\", \"5 4 3\\n3 4\\n3 1\\n3 3\\n5 3\\n1 3\\n1 4\\n\", \"1 1 10\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 5\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n8 3\\n5 1\\n10 4\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n4 2\\n7 8\\n3 3\\n4 2\\n6 10\\n9 4\\n10 2\\n7 7\\n\", \"2 5 2\\n1 1\\n1 1\\n1 1\\n1 1\\n\", \"2 2 2\\n2 1\\n2 1\\n1 2\\n1 1\\n\", \"2 2 1\\n1 1\\n1 1\\n\", \"2 2 1\\n1 1\\n2 2\\n\", \"3 3 2\\n1 2\\n2 1\\n3 3\\n3 2\\n\", \"2 2 1\\n1 1\\n1 1\\n\", \"2 2 2\\n2 1\\n2 1\\n1 2\\n1 1\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 5\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n8 3\\n5 1\\n10 4\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n4 2\\n7 8\\n3 3\\n4 2\\n6 10\\n9 4\\n10 2\\n7 7\\n\", \"5 4 3\\n3 4\\n3 1\\n3 3\\n5 3\\n1 3\\n1 4\\n\", \"2 2 1\\n1 1\\n2 2\\n\", \"1 1 10\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n\", \"2 5 2\\n1 1\\n1 1\\n1 1\\n1 1\\n\", \"3 3 2\\n1 2\\n2 2\\n3 3\\n3 2\\n\", \"3 2 1\\n1 1\\n1 1\\n\", \"2 2 2\\n2 1\\n2 1\\n1 2\\n2 1\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 5\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n8 3\\n5 1\\n10 4\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n4 2\\n7 8\\n3 3\\n4 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"5 4 3\\n3 4\\n3 1\\n3 1\\n5 3\\n1 3\\n1 4\\n\", \"1 1 10\\n1 1\\n1 1\\n1 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n\", \"2 5 2\\n0 1\\n1 1\\n1 1\\n1 1\\n\", \"2 6 2\\n0 1\\n1 1\\n1 1\\n1 1\\n\", \"5 3 2\\n3 4\\n3 1\\n3 3\\n5 0\\n1 3\\n0 8\\n\", \"1 3 2\\n0 2\\n0 2\\n0 5\\n3 2\\n\", \"4 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n1 3\\n0 8\\n\", \"1 2 7\\n1 1\\n1 1\\n0 1\\n2 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 2\\n1 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 -1\\n1 1\\n1 1\\n\", \"8 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n1 3\\n0 16\\n\", \"1 10 20\\n7 5\\n4 4\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n9 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 4 7\\n1 1\\n0 1\\n0 1\\n3 0\\n1 1\\n2 1\\n1 1\\n1 0\\n1 2\\n1 0\\n1 2\\n1 0\\n0 1\\n1 1\\n1 2\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"2 2 1\\n2 1\\n2 2\\n\", \"5 4 3\\n3 4\\n3 1\\n3 3\\n5 0\\n1 3\\n1 4\\n\", \"3 3 2\\n1 2\\n2 1\\n3 5\\n3 2\\n\", \"2 2 2\\n2 1\\n2 2\\n1 2\\n2 1\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 5\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n8 3\\n5 1\\n10 4\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n4 2\\n7 8\\n3 3\\n0 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 10\\n1 1\\n1 1\\n1 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 1\\n1 1\\n\", \"5 4 3\\n3 4\\n3 1\\n3 3\\n5 0\\n1 3\\n1 8\\n\", \"3 3 2\\n1 2\\n0 1\\n3 5\\n3 2\\n\", \"2 2 2\\n2 1\\n1 2\\n1 2\\n2 1\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 5\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n8 3\\n5 1\\n10 8\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n4 2\\n7 8\\n3 3\\n0 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 10\\n1 1\\n1 1\\n2 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 1\\n1 1\\n\", \"2 6 2\\n0 1\\n1 1\\n1 2\\n1 1\\n\", \"5 4 2\\n3 4\\n3 1\\n3 3\\n5 0\\n1 3\\n1 8\\n\", \"3 3 2\\n1 2\\n0 1\\n0 5\\n3 2\\n\", \"2 2 2\\n2 0\\n1 2\\n1 2\\n2 1\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 5\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n8 3\\n5 1\\n10 8\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n4 2\\n7 8\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 10\\n1 1\\n1 1\\n2 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 2\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 1\\n1 1\\n\", \"2 6 2\\n0 1\\n1 1\\n1 2\\n2 1\\n\", \"5 4 2\\n3 4\\n3 1\\n3 3\\n5 0\\n1 3\\n0 8\\n\", \"3 3 2\\n0 2\\n0 1\\n0 5\\n3 2\\n\", \"2 2 2\\n2 0\\n1 2\\n1 2\\n3 1\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 5\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n8 3\\n5 1\\n10 8\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n2 2\\n7 8\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 10\\n1 1\\n1 1\\n2 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 1\\n1 1\\n\", \"2 2 2\\n0 1\\n1 1\\n1 2\\n2 1\\n\", \"3 3 2\\n0 2\\n0 2\\n0 5\\n3 2\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 5\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n8 3\\n5 1\\n10 8\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 10\\n1 1\\n1 1\\n2 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 1\\n1 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 1\\n1 1\\n\", \"2 2 2\\n0 1\\n1 1\\n1 2\\n2 2\\n\", \"3 3 2\\n3 4\\n3 1\\n3 3\\n5 0\\n1 3\\n0 8\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 5\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 7\\n1 1\\n1 1\\n2 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 1\\n1 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 1\\n1 1\\n\", \"2 2 2\\n0 2\\n1 1\\n1 2\\n2 2\\n\", \"3 3 2\\n3 4\\n3 1\\n3 3\\n10 0\\n1 3\\n0 8\\n\", \"1 3 2\\n0 1\\n0 2\\n0 5\\n3 2\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n3 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 7\\n1 1\\n1 1\\n2 1\\n2 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 1\\n1 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 1\\n1 1\\n\", \"3 3 2\\n3 4\\n3 1\\n3 2\\n10 0\\n1 3\\n0 8\\n\", \"1 3 2\\n0 1\\n0 2\\n0 4\\n3 2\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n6 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 7\\n1 1\\n1 1\\n2 1\\n2 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 2\\n1 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 1\\n1 1\\n\", \"3 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n1 3\\n0 8\\n\", \"1 3 2\\n0 1\\n0 2\\n0 4\\n1 2\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n6 2\\n1 1\\n10 9\\n7 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 7\\n1 1\\n1 1\\n0 1\\n2 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 2\\n1 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 1\\n1 1\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n9 2\\n1 1\\n10 9\\n7 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n1 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 1 7\\n1 1\\n1 1\\n0 1\\n2 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 2\\n1 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 -1\\n1 1\\n1 1\\n\", \"4 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n1 3\\n0 16\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n9 2\\n1 1\\n10 9\\n7 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n8 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"10 10 20\\n7 5\\n4 5\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n9 2\\n1 1\\n10 9\\n7 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 2 7\\n1 1\\n1 1\\n0 1\\n2 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 2\\n1 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"8 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n1 3\\n0 13\\n\", \"10 10 20\\n7 5\\n4 4\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n9 2\\n1 1\\n10 9\\n7 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 2 7\\n1 1\\n1 1\\n0 1\\n2 0\\n1 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 2\\n1 0\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"3 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n1 3\\n0 13\\n\", \"10 10 20\\n7 5\\n4 4\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n8 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n9 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 2 7\\n1 1\\n1 1\\n0 1\\n2 0\\n1 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 4\\n1 2\\n1 0\\n1 1\\n1 1\\n1 2\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"3 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n1 3\\n1 13\\n\", \"1 2 7\\n1 1\\n1 1\\n0 1\\n2 0\\n1 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 2\\n1 0\\n1 1\\n1 1\\n1 2\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"3 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n1 3\\n1 11\\n\", \"1 10 20\\n7 5\\n4 4\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n9 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n4 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 2 7\\n1 1\\n1 1\\n0 1\\n2 0\\n1 1\\n2 1\\n1 1\\n1 1\\n1 1\\n1 0\\n1 2\\n1 0\\n0 1\\n1 1\\n1 2\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"3 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n2 3\\n1 11\\n\", \"1 10 20\\n7 5\\n4 4\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n9 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 2 7\\n1 1\\n1 1\\n0 1\\n2 0\\n1 1\\n2 1\\n1 1\\n1 0\\n1 1\\n1 0\\n1 2\\n1 0\\n0 1\\n1 1\\n1 2\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"3 3 2\\n3 4\\n3 1\\n3 2\\n13 0\\n2 0\\n1 11\\n\", \"1 10 20\\n7 5\\n4 4\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n5 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n8 2\\n10 3\\n5 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 2 7\\n1 1\\n0 1\\n0 1\\n2 0\\n1 1\\n2 1\\n1 1\\n1 0\\n1 1\\n1 0\\n1 2\\n1 0\\n0 1\\n1 1\\n1 2\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"1 10 20\\n7 5\\n4 4\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n5 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n1 2\\n10 3\\n5 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 2 7\\n1 1\\n0 1\\n0 1\\n3 0\\n1 1\\n2 1\\n1 1\\n1 0\\n1 1\\n1 0\\n1 2\\n1 0\\n0 1\\n1 1\\n1 2\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"1 10 20\\n7 5\\n4 4\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 4\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n5 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n1 2\\n10 3\\n8 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 2 7\\n1 1\\n0 1\\n0 1\\n3 0\\n1 1\\n2 1\\n1 1\\n1 0\\n1 2\\n1 0\\n1 2\\n1 0\\n0 1\\n1 1\\n1 2\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"1 10 20\\n7 5\\n4 4\\n5 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 0\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n5 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n1 2\\n10 3\\n8 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 10 20\\n7 5\\n4 4\\n10 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 0\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n5 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n1 2\\n10 3\\n8 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 9\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 4 7\\n1 1\\n0 1\\n0 1\\n3 0\\n1 1\\n2 1\\n1 1\\n1 0\\n1 2\\n1 0\\n1 2\\n1 0\\n0 1\\n1 1\\n1 4\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 1\\n\", \"1 10 20\\n7 5\\n4 4\\n10 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 0\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n5 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n1 2\\n10 3\\n8 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 3\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n9 4\\n10 2\\n7 7\\n\", \"1 4 7\\n1 1\\n0 1\\n0 1\\n3 0\\n1 1\\n2 1\\n1 1\\n1 0\\n1 2\\n1 0\\n1 2\\n1 0\\n0 1\\n1 1\\n1 4\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 2\\n\", \"1 10 20\\n7 5\\n4 4\\n10 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 0\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n5 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 4\\n1 2\\n10 3\\n8 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 3\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n10 4\\n10 2\\n7 7\\n\", \"1 4 7\\n0 1\\n0 1\\n0 1\\n3 0\\n1 1\\n2 1\\n1 1\\n1 0\\n1 2\\n1 0\\n1 2\\n1 0\\n0 1\\n1 1\\n1 4\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 2\\n\", \"1 10 20\\n7 5\\n4 4\\n10 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 0\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n5 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 1\\n1 2\\n10 3\\n8 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 3\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n10 4\\n10 2\\n7 7\\n\", \"1 4 7\\n0 1\\n0 1\\n0 1\\n3 0\\n1 1\\n2 1\\n1 1\\n1 0\\n1 2\\n1 0\\n1 3\\n1 0\\n0 1\\n1 1\\n1 4\\n1 1\\n1 1\\n1 -1\\n1 1\\n0 2\\n\", \"1 10 20\\n14 5\\n4 4\\n10 4\\n7 4\\n1 5\\n6 7\\n9 10\\n10 4\\n1 0\\n2 10\\n3 10\\n4 10\\n0 6\\n5 7\\n5 2\\n1 1\\n10 9\\n5 6\\n1 4\\n11 1\\n1 2\\n10 3\\n8 1\\n10 8\\n8 2\\n2 9\\n1 10\\n9 5\\n2 2\\n6 7\\n7 6\\n8 3\\n2 2\\n7 1\\n3 3\\n1 2\\n6 20\\n10 4\\n10 2\\n7 7\\n\", \"5 4 3\\n3 4\\n3 1\\n3 3\\n5 3\\n1 3\\n1 4\\n\", \"3 3 2\\n1 2\\n2 1\\n3 3\\n3 2\\n\"], \"outputs\": [\"12\\nUULLRRDLLDRR\", \"26\\nUUUULLLRRRDLLLDRRRDLLLDRRR\", \"0\\n\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"14\\nULLLLRRRRDLLLL\", \"5\\nULRDL\", \"5\\nULRDL\", \"5\\nULRDL\", \"12\\nUULLRRDLLDRR\", \"5\\nULRDL\", \"5\\nULRDL\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"26\\nUUUULLLRRRDLLLDRRRDLLLDRRR\", \"5\\nULRDL\", \"0\\n\", \"14\\nULLLLRRRRDLLLL\", \"12\\nUULLRRDLLDRR\", \"8\\nUULRDLDR\", \"5\\nULRDL\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"26\\nUUUULLLRRRDLLLDRRRDLLLDRRR\", \"0\\n\", \"14\\nULLLLRRRRDLLLL\", \"17\\nULLLLLRRRRRDLLLLL\", \"20\\nUUUULLRRDLLDRRDLLDRR\", \"4\\nLLRR\", \"16\\nUUULLRRDLLDRRDLL\", \"2\\nLR\", \"32\\nUUUUUUULLRRDLLDRRDLLDRRDLLDRRDLL\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"6\\nLLLRRR\", \"5\\nULRDL\", \"26\\nUUUULLLRRRDLLLDRRRDLLLDRRR\", \"12\\nUULLRRDLLDRR\", \"5\\nULRDL\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"26\\nUUUULLLRRRDLLLDRRRDLLLDRRR\", \"12\\nUULLRRDLLDRR\", \"5\\nULRDL\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"17\\nULLLLLRRRRRDLLLLL\", \"26\\nUUUULLLRRRDLLLDRRRDLLLDRRR\", \"12\\nUULLRRDLLDRR\", \"5\\nULRDL\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"17\\nULLLLLRRRRRDLLLLL\", \"26\\nUUUULLLRRRDLLLDRRRDLLLDRRR\", \"12\\nUULLRRDLLDRR\", \"5\\nULRDL\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"5\\nULRDL\", \"12\\nUULLRRDLLDRR\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"5\\nULRDL\", \"12\\nUULLRRDLLDRR\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"5\\nULRDL\", \"12\\nUULLRRDLLDRR\", \"4\\nLLRR\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"12\\nUULLRRDLLDRR\", \"4\\nLLRR\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"12\\nUULLRRDLLDRR\", \"4\\nLLRR\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"0\\n\", \"16\\nUUULLRRDLLDRRDLL\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"2\\nLR\", \"32\\nUUUUUUULLRRDLLDRRDLLDRRDLLDRRDLL\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"2\\nLR\", \"12\\nUULLRRDLLDRR\", \"117\\nUUUUUUUUULLLLLLLLLRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLLDRRRRRRRRRDLLLLLLLLL\", \"2\\nLR\", \"12\\nUULLRRDLLDRR\", \"2\\nLR\", \"12\\nUULLRRDLLDRR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"2\\nLR\", \"12\\nUULLRRDLLDRR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"2\\nLR\", \"12\\nUULLRRDLLDRR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"2\\nLR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"2\\nLR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"2\\nLR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"6\\nLLLRRR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"6\\nLLLRRR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"6\\nLLLRRR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"6\\nLLLRRR\", \"18\\nLLLLLLLLLRRRRRRRRR\", \"26\\nUUUULLLRRRDLLLDRRRDLLLDRRR\", \"12\\nUULLRRDLLDRR\"]}", "source": "taco"}
|
Petya has a rectangular Board of size $n \times m$. Initially, $k$ chips are placed on the board, $i$-th chip is located in the cell at the intersection of $sx_i$-th row and $sy_i$-th column.
In one action, Petya can move all the chips to the left, right, down or up by $1$ cell.
If the chip was in the $(x, y)$ cell, then after the operation: left, its coordinates will be $(x, y - 1)$; right, its coordinates will be $(x, y + 1)$; down, its coordinates will be $(x + 1, y)$; up, its coordinates will be $(x - 1, y)$.
If the chip is located by the wall of the board, and the action chosen by Petya moves it towards the wall, then the chip remains in its current position.
Note that several chips can be located in the same cell.
For each chip, Petya chose the position which it should visit. Note that it's not necessary for a chip to end up in this position.
Since Petya does not have a lot of free time, he is ready to do no more than $2nm$ actions.
You have to find out what actions Petya should do so that each chip visits the position that Petya selected for it at least once. Or determine that it is not possible to do this in $2nm$ actions.
-----Input-----
The first line contains three integers $n, m, k$ ($1 \le n, m, k \le 200$) — the number of rows and columns of the board and the number of chips, respectively.
The next $k$ lines contains two integers each $sx_i, sy_i$ ($ 1 \le sx_i \le n, 1 \le sy_i \le m$) — the starting position of the $i$-th chip.
The next $k$ lines contains two integers each $fx_i, fy_i$ ($ 1 \le fx_i \le n, 1 \le fy_i \le m$) — the position that the $i$-chip should visit at least once.
-----Output-----
In the first line print the number of operations so that each chip visits the position that Petya selected for it at least once.
In the second line output the sequence of operations. To indicate operations left, right, down, and up, use the characters $L, R, D, U$ respectively.
If the required sequence does not exist, print -1 in the single line.
-----Examples-----
Input
3 3 2
1 2
2 1
3 3
3 2
Output
3
DRD
Input
5 4 3
3 4
3 1
3 3
5 3
1 3
1 4
Output
9
DDLUUUURR
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"2\\n\", \"13\\n\", \"720\\n\", \"0\\n\", \"1\\n\", \"3\\n\", \"4\\n\", \"5\\n\", \"6\\n\", \"637\\n\", \"7\\n\", \"8\\n\", \"9\\n\", \"10\\n\", \"11\\n\", \"100\\n\", \"99\\n\", \"245\\n\", \"118\\n\", \"429\\n\", \"555\\n\", \"660\\n\", \"331\\n\", \"987\\n\", \"123456789\\n\", \"234567890\\n\", \"100000000\\n\", \"111111111\\n\", \"90909090\\n\", \"987654321\\n\", \"45165125\\n\", \"445511006\\n\", \"999999999\\n\", \"984218523\\n\", \"19\\n\", \"10000000\\n\", \"111111111\\n\", \"0\\n\", \"331\\n\", \"9\\n\", \"987654321\\n\", \"10\\n\", \"999999999\\n\", \"234567890\\n\", \"123456789\\n\", \"987\\n\", \"984218523\\n\", \"45165125\\n\", \"555\\n\", \"660\\n\", \"118\\n\", \"7\\n\", \"1\\n\", \"100000000\\n\", \"6\\n\", \"637\\n\", \"11\\n\", \"90909090\\n\", \"429\\n\", \"4\\n\", \"99\\n\", \"3\\n\", \"100\\n\", \"8\\n\", \"10000000\\n\", \"5\\n\", \"245\\n\", \"19\\n\", \"445511006\\n\", \"606\\n\", \"16\\n\", \"988644283\\n\", \"18\\n\", \"1116434957\\n\", \"410231283\\n\", \"159065739\\n\", \"1161\\n\", \"107637737\\n\", \"29149803\\n\", \"358\\n\", \"423\\n\", \"75\\n\", \"14\\n\", \"110000000\\n\", \"470\\n\", \"24\\n\", \"86485087\\n\", \"62\\n\", \"135\\n\", \"15\\n\", \"22\\n\", \"10000010\\n\", \"406\\n\", \"21\\n\", \"861511185\\n\", \"1000\\n\", \"12\\n\", \"723\\n\", \"1603481361\\n\", \"25\\n\", \"1231106676\\n\", \"508078385\\n\", \"23740405\\n\", \"1834\\n\", \"49485144\\n\", \"43168627\\n\", \"95\\n\", \"626\\n\", \"44\\n\", \"23\\n\", \"605\\n\", \"40\\n\", \"4382991\\n\", \"50\\n\", \"10000011\\n\", \"185\\n\", \"31\\n\", \"1187740078\\n\", \"26\\n\", \"910\\n\", \"43\\n\", \"566131607\\n\", \"570298308\\n\", \"10634662\\n\", \"2231\\n\", \"73280676\\n\", \"75251959\\n\", \"59\\n\", \"667\\n\", \"37\\n\", \"35\\n\", \"734\\n\", \"1536010\\n\", \"68\\n\", \"10000111\\n\", \"316\\n\", \"65\\n\", \"402275267\\n\", \"70\\n\", \"1112\\n\", \"51\\n\", \"514730347\\n\", \"939052485\\n\", \"12357923\\n\", \"1386\\n\", \"136256169\\n\", \"140757155\\n\", \"94\\n\", \"124\\n\", \"27\\n\", \"29\\n\", \"312\\n\", \"2897022\\n\", \"79\\n\", \"10100111\\n\", \"601\\n\", \"119\\n\", \"497212605\\n\", \"30\\n\", \"1431\\n\", \"348034922\\n\", \"575534719\\n\", \"17394848\\n\", \"2\\n\", \"720\\n\", \"13\\n\"], \"outputs\": [\"O-|OO-OO\\n\", \"O-|OOO-O\\nO-|O-OOO\\n\", \"O-|-OOOO\\nO-|OO-OO\\n-O|OO-OO\\n\", \"O-|-OOOO\\n\", \"O-|O-OOO\\n\", \"O-|OOO-O\\n\", \"O-|OOOO-\\n\", \"-O|-OOOO\\n\", \"-O|O-OOO\\n\", \"-O|OO-OO\\nO-|OOO-O\\n-O|O-OOO\\n\", \"-O|OO-OO\\n\", \"-O|OOO-O\\n\", \"-O|OOOO-\\n\", \"O-|-OOOO\\nO-|O-OOO\\n\", \"O-|O-OOO\\nO-|O-OOO\\n\", \"O-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"-O|OOOO-\\n-O|OOOO-\\n\", \"-O|-OOOO\\nO-|OOOO-\\nO-|OO-OO\\n\", \"-O|OOO-O\\nO-|O-OOO\\nO-|O-OOO\\n\", \"-O|OOOO-\\nO-|OO-OO\\nO-|OOOO-\\n\", \"-O|-OOOO\\n-O|-OOOO\\n-O|-OOOO\\n\", \"O-|-OOOO\\n-O|O-OOO\\n-O|O-OOO\\n\", \"O-|O-OOO\\nO-|OOO-O\\nO-|OOO-O\\n\", \"-O|OO-OO\\n-O|OOO-O\\n-O|OOOO-\\n\", \"-O|OOOO-\\n-O|OOO-O\\n-O|OO-OO\\n-O|O-OOO\\n-O|-OOOO\\nO-|OOOO-\\nO-|OOO-O\\nO-|OO-OO\\nO-|O-OOO\\n\", \"O-|-OOOO\\n-O|OOOO-\\n-O|OOO-O\\n-O|OO-OO\\n-O|O-OOO\\n-O|-OOOO\\nO-|OOOO-\\nO-|OOO-O\\nO-|OO-OO\\n\", \"O-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"O-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\n\", \"O-|-OOOO\\n-O|OOOO-\\nO-|-OOOO\\n-O|OOOO-\\nO-|-OOOO\\n-O|OOOO-\\nO-|-OOOO\\n-O|OOOO-\\n\", \"O-|O-OOO\\nO-|OO-OO\\nO-|OOO-O\\nO-|OOOO-\\n-O|-OOOO\\n-O|O-OOO\\n-O|OO-OO\\n-O|OOO-O\\n-O|OOOO-\\n\", \"-O|-OOOO\\nO-|OO-OO\\nO-|O-OOO\\n-O|-OOOO\\n-O|O-OOO\\nO-|O-OOO\\n-O|-OOOO\\nO-|OOOO-\\n\", \"-O|O-OOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\nO-|O-OOO\\n-O|-OOOO\\n-O|-OOOO\\nO-|OOOO-\\nO-|OOOO-\\n\", \"-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n\", \"O-|OOO-O\\nO-|OO-OO\\n-O|-OOOO\\n-O|OOO-O\\nO-|O-OOO\\nO-|OO-OO\\nO-|OOOO-\\n-O|OOO-O\\n-O|OOOO-\\n\", \"-O|OOOO-\\nO-|O-OOO\\n\", \"O-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"O-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\n\", \"O-|-OOOO\\n\", \"O-|O-OOO\\nO-|OOO-O\\nO-|OOO-O\\n\", \"-O|OOOO-\\n\", \"O-|O-OOO\\nO-|OO-OO\\nO-|OOO-O\\nO-|OOOO-\\n-O|-OOOO\\n-O|O-OOO\\n-O|OO-OO\\n-O|OOO-O\\n-O|OOOO-\\n\", \"O-|-OOOO\\nO-|O-OOO\\n\", \"-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n-O|OOOO-\\n\", \"O-|-OOOO\\n-O|OOOO-\\n-O|OOO-O\\n-O|OO-OO\\n-O|O-OOO\\n-O|-OOOO\\nO-|OOOO-\\nO-|OOO-O\\nO-|OO-OO\\n\", \"-O|OOOO-\\n-O|OOO-O\\n-O|OO-OO\\n-O|O-OOO\\n-O|-OOOO\\nO-|OOOO-\\nO-|OOO-O\\nO-|OO-OO\\nO-|O-OOO\\n\", \"-O|OO-OO\\n-O|OOO-O\\n-O|OOOO-\\n\", \"O-|OOO-O\\nO-|OO-OO\\n-O|-OOOO\\n-O|OOO-O\\nO-|O-OOO\\nO-|OO-OO\\nO-|OOOO-\\n-O|OOO-O\\n-O|OOOO-\\n\", \"-O|-OOOO\\nO-|OO-OO\\nO-|O-OOO\\n-O|-OOOO\\n-O|O-OOO\\nO-|O-OOO\\n-O|-OOOO\\nO-|OOOO-\\n\", \"-O|-OOOO\\n-O|-OOOO\\n-O|-OOOO\\n\", \"O-|-OOOO\\n-O|O-OOO\\n-O|O-OOO\\n\", \"-O|OOO-O\\nO-|O-OOO\\nO-|O-OOO\\n\", \"-O|OO-OO\\n\", \"O-|O-OOO\\n\", \"O-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"-O|O-OOO\\n\", \"-O|OO-OO\\nO-|OOO-O\\n-O|O-OOO\\n\", \"O-|O-OOO\\nO-|O-OOO\\n\", \"O-|-OOOO\\n-O|OOOO-\\nO-|-OOOO\\n-O|OOOO-\\nO-|-OOOO\\n-O|OOOO-\\nO-|-OOOO\\n-O|OOOO-\\n\", \"-O|OOOO-\\nO-|OO-OO\\nO-|OOOO-\\n\", \"O-|OOOO-\\n\", \"-O|OOOO-\\n-O|OOOO-\\n\", \"O-|OOO-O\\n\", \"O-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"-O|OOO-O\\n\", \"O-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"-O|-OOOO\\n\", \"-O|-OOOO\\nO-|OOOO-\\nO-|OO-OO\\n\", \"-O|OOOO-\\nO-|O-OOO\\n\", \"-O|O-OOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\nO-|O-OOO\\n-O|-OOOO\\n-O|-OOOO\\nO-|OOOO-\\nO-|OOOO-\\n\", \"-O|O-OOO\\nO-|-OOOO\\n-O|O-OOO\\n\", \"-O|O-OOO\\nO-|O-OOO\\n\", \"O-|OOO-O\\n-O|OOO-O\\nO-|OO-OO\\nO-|OOOO-\\nO-|OOOO-\\n-O|O-OOO\\n-O|OOO-O\\n-O|OOO-O\\n-O|OOOO-\\n\", \"-O|OOO-O\\nO-|O-OOO\\n\", \"-O|OO-OO\\n-O|-OOOO\\n-O|OOOO-\\nO-|OOOO-\\nO-|OOO-O\\nO-|OOOO-\\n-O|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\n\", \"O-|OOO-O\\n-O|OOO-O\\nO-|OO-OO\\nO-|O-OOO\\nO-|OOO-O\\nO-|OO-OO\\nO-|-OOOO\\nO-|O-OOO\\nO-|OOOO-\\n\", \"-O|OOOO-\\nO-|OOO-O\\n-O|OO-OO\\n-O|-OOOO\\n-O|O-OOO\\nO-|-OOOO\\n-O|OOOO-\\n-O|-OOOO\\nO-|O-OOO\\n\", \"O-|O-OOO\\n-O|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\n\", \"-O|OO-OO\\nO-|OOO-O\\n-O|OO-OO\\n-O|OO-OO\\nO-|OOO-O\\n-O|O-OOO\\n-O|OO-OO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"O-|OOO-O\\nO-|-OOOO\\n-O|OOO-O\\n-O|OOOO-\\nO-|OOOO-\\nO-|O-OOO\\n-O|OOOO-\\nO-|OO-OO\\n\", \"-O|OOO-O\\n-O|-OOOO\\nO-|OOO-O\\n\", \"O-|OOO-O\\nO-|OO-OO\\nO-|OOOO-\\n\", \"-O|-OOOO\\n-O|OO-OO\\n\", \"O-|OOOO-\\nO-|O-OOO\\n\", \"O-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\nO-|O-OOO\\n\", \"O-|-OOOO\\n-O|OO-OO\\nO-|OOOO-\\n\", \"O-|OOOO-\\nO-|OO-OO\\n\", \"-O|OO-OO\\n-O|OOO-O\\nO-|-OOOO\\n-O|-OOOO\\n-O|OOO-O\\nO-|OOOO-\\n-O|O-OOO\\n-O|OOO-O\\n\", \"O-|OO-OO\\n-O|O-OOO\\n\", \"-O|-OOOO\\nO-|OOO-O\\nO-|O-OOO\\n\", \"-O|-OOOO\\nO-|O-OOO\\n\", \"O-|OO-OO\\nO-|OO-OO\\n\", \"O-|-OOOO\\nO-|O-OOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"-O|O-OOO\\nO-|-OOOO\\nO-|OOOO-\\n\", \"O-|O-OOO\\nO-|OO-OO\\n\", \"-O|-OOOO\\n-O|OOO-O\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\n-O|-OOOO\\nO-|O-OOO\\n-O|O-OOO\\n-O|OOO-O\\n\", \"O-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"O-|OO-OO\\nO-|O-OOO\\n\", \"O-|OOO-O\\nO-|OO-OO\\n-O|OO-OO\\n\", \"O-|O-OOO\\n-O|O-OOO\\nO-|OOO-O\\nO-|O-OOO\\n-O|OOO-O\\nO-|OOOO-\\nO-|OOO-O\\nO-|-OOOO\\n-O|O-OOO\\nO-|O-OOO\\n\", \"-O|-OOOO\\nO-|OO-OO\\n\", \"-O|O-OOO\\n-O|OO-OO\\n-O|O-OOO\\n-O|O-OOO\\nO-|-OOOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|OOO-O\\nO-|OO-OO\\nO-|O-OOO\\n\", \"-O|-OOOO\\n-O|OOO-O\\nO-|OOO-O\\n-O|OOO-O\\n-O|OO-OO\\nO-|-OOOO\\n-O|OOO-O\\nO-|-OOOO\\n-O|-OOOO\\n\", \"-O|-OOOO\\nO-|-OOOO\\nO-|OOOO-\\nO-|-OOOO\\nO-|OOOO-\\n-O|OO-OO\\nO-|OOO-O\\nO-|OO-OO\\n\", \"O-|OOOO-\\nO-|OOO-O\\n-O|OOO-O\\nO-|O-OOO\\n\", \"O-|OOOO-\\nO-|OOOO-\\nO-|O-OOO\\n-O|-OOOO\\n-O|OOO-O\\nO-|OOOO-\\n-O|OOOO-\\nO-|OOOO-\\n\", \"-O|OO-OO\\nO-|OO-OO\\n-O|O-OOO\\n-O|OOO-O\\n-O|O-OOO\\nO-|O-OOO\\nO-|OOO-O\\nO-|OOOO-\\n\", \"-O|-OOOO\\n-O|OOOO-\\n\", \"-O|O-OOO\\nO-|OO-OO\\n-O|O-OOO\\n\", \"O-|OOOO-\\nO-|OOOO-\\n\", \"O-|OOO-O\\nO-|OO-OO\\n\", \"-O|-OOOO\\nO-|-OOOO\\n-O|O-OOO\\n\", \"O-|-OOOO\\nO-|OOOO-\\n\", \"O-|O-OOO\\n-O|OOOO-\\n-O|OOOO-\\nO-|OO-OO\\n-O|OOO-O\\nO-|OOO-O\\nO-|OOOO-\\n\", \"O-|-OOOO\\n-O|-OOOO\\n\", \"O-|O-OOO\\nO-|O-OOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"-O|-OOOO\\n-O|OOO-O\\nO-|O-OOO\\n\", \"O-|O-OOO\\nO-|OOO-O\\n\", \"-O|OOO-O\\n-O|OO-OO\\nO-|-OOOO\\nO-|-OOOO\\nO-|OOOO-\\n-O|OO-OO\\n-O|OO-OO\\n-O|OOO-O\\nO-|O-OOO\\nO-|O-OOO\\n\", \"-O|O-OOO\\nO-|OO-OO\\n\", \"O-|-OOOO\\nO-|O-OOO\\n-O|OOOO-\\n\", \"O-|OOO-O\\nO-|OOOO-\\n\", \"-O|OO-OO\\nO-|-OOOO\\n-O|O-OOO\\nO-|O-OOO\\nO-|OOO-O\\nO-|O-OOO\\n-O|O-OOO\\n-O|O-OOO\\n-O|-OOOO\\n\", \"-O|OOO-O\\nO-|-OOOO\\nO-|OOO-O\\n-O|OOO-O\\n-O|OOOO-\\nO-|OO-OO\\nO-|-OOOO\\n-O|OO-OO\\n-O|-OOOO\\n\", \"O-|OO-OO\\n-O|O-OOO\\n-O|O-OOO\\nO-|OOOO-\\nO-|OOO-O\\n-O|O-OOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"O-|O-OOO\\nO-|OOO-O\\nO-|OO-OO\\nO-|OO-OO\\n\", \"-O|O-OOO\\n-O|OO-OO\\n-O|O-OOO\\nO-|-OOOO\\n-O|OOO-O\\nO-|OO-OO\\nO-|OOO-O\\n-O|OO-OO\\n\", \"-O|OOOO-\\n-O|-OOOO\\n-O|OOOO-\\nO-|O-OOO\\n-O|-OOOO\\nO-|OO-OO\\n-O|-OOOO\\n-O|OO-OO\\n\", \"-O|OOOO-\\n-O|-OOOO\\n\", \"-O|OO-OO\\n-O|O-OOO\\n-O|O-OOO\\n\", \"-O|OO-OO\\nO-|OOO-O\\n\", \"-O|-OOOO\\nO-|OOO-O\\n\", \"O-|OOOO-\\nO-|OOO-O\\n-O|OO-OO\\n\", \"O-|-OOOO\\nO-|O-OOO\\nO-|-OOOO\\n-O|O-OOO\\nO-|OOO-O\\n-O|-OOOO\\nO-|O-OOO\\n\", \"-O|OOO-O\\n-O|O-OOO\\n\", \"O-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"-O|O-OOO\\nO-|O-OOO\\nO-|OOO-O\\n\", \"-O|-OOOO\\n-O|O-OOO\\n\", \"-O|OO-OO\\n-O|O-OOO\\nO-|OO-OO\\n-O|-OOOO\\n-O|OO-OO\\nO-|OO-OO\\nO-|OO-OO\\nO-|-OOOO\\nO-|OOOO-\\n\", \"O-|-OOOO\\n-O|OO-OO\\n\", \"O-|OO-OO\\nO-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\n\", \"O-|O-OOO\\n-O|-OOOO\\n\", \"-O|OO-OO\\nO-|OOOO-\\nO-|OOO-O\\nO-|-OOOO\\nO-|OOO-O\\n-O|OO-OO\\nO-|OOOO-\\nO-|O-OOO\\n-O|-OOOO\\n\", \"-O|-OOOO\\n-O|OOO-O\\nO-|OOOO-\\nO-|OO-OO\\n-O|-OOOO\\nO-|-OOOO\\n-O|OOOO-\\nO-|OOO-O\\n-O|OOOO-\\n\", \"O-|OOO-O\\nO-|OO-OO\\n-O|OOOO-\\n-O|OO-OO\\n-O|-OOOO\\nO-|OOO-O\\nO-|OO-OO\\nO-|O-OOO\\n\", \"-O|O-OOO\\n-O|OOO-O\\nO-|OOO-O\\nO-|O-OOO\\n\", \"-O|OOOO-\\n-O|O-OOO\\nO-|O-OOO\\n-O|O-OOO\\n-O|-OOOO\\nO-|OO-OO\\n-O|O-OOO\\nO-|OOO-O\\nO-|O-OOO\\n\", \"-O|-OOOO\\n-O|-OOOO\\nO-|O-OOO\\n-O|OO-OO\\n-O|-OOOO\\n-O|OO-OO\\nO-|-OOOO\\nO-|OOOO-\\nO-|O-OOO\\n\", \"O-|OOOO-\\n-O|OOOO-\\n\", \"O-|OOOO-\\nO-|OO-OO\\nO-|O-OOO\\n\", \"-O|OO-OO\\nO-|OO-OO\\n\", \"-O|OOOO-\\nO-|OO-OO\\n\", \"O-|OO-OO\\nO-|O-OOO\\nO-|OOO-O\\n\", \"O-|OO-OO\\nO-|OO-OO\\nO-|-OOOO\\n-O|OO-OO\\n-O|OOOO-\\n-O|OOO-O\\nO-|OO-OO\\n\", \"-O|OOOO-\\n-O|OO-OO\\n\", \"O-|O-OOO\\nO-|O-OOO\\nO-|O-OOO\\nO-|-OOOO\\nO-|-OOOO\\nO-|O-OOO\\nO-|-OOOO\\nO-|O-OOO\\n\", \"O-|O-OOO\\nO-|-OOOO\\n-O|O-OOO\\n\", \"-O|OOOO-\\nO-|O-OOO\\nO-|O-OOO\\n\", \"-O|-OOOO\\nO-|-OOOO\\n-O|O-OOO\\nO-|OO-OO\\nO-|O-OOO\\nO-|OO-OO\\n-O|OO-OO\\n-O|OOOO-\\nO-|OOOO-\\n\", \"O-|-OOOO\\nO-|OOO-O\\n\", \"O-|O-OOO\\nO-|OOO-O\\nO-|OOOO-\\nO-|O-OOO\\n\", \"O-|OO-OO\\nO-|OO-OO\\n-O|OOOO-\\nO-|OOOO-\\nO-|OOO-O\\nO-|-OOOO\\n-O|OOO-O\\nO-|OOOO-\\nO-|OOO-O\\n\", \"-O|OOOO-\\nO-|O-OOO\\n-O|OO-OO\\nO-|OOOO-\\nO-|OOO-O\\n-O|-OOOO\\n-O|-OOOO\\n-O|OO-OO\\n-O|-OOOO\\n\", \"-O|OOO-O\\nO-|OOOO-\\n-O|OOO-O\\nO-|OOOO-\\n-O|OOOO-\\nO-|OOO-O\\n-O|OO-OO\\nO-|O-OOO\\n\", \"O-|OO-OO\\n\", \"O-|-OOOO\\nO-|OO-OO\\n-O|OO-OO\\n\", \"O-|OOO-O\\nO-|O-OOO\\n\"]}", "source": "taco"}
|
You know that Japan is the country with almost the largest 'electronic devices per person' ratio. So you might be quite surprised to find out that the primary school in Japan teaches to count using a Soroban — an abacus developed in Japan. This phenomenon has its reasons, of course, but we are not going to speak about them. Let's have a look at the Soroban's construction. [Image]
Soroban consists of some number of rods, each rod contains five beads. We will assume that the rods are horizontal lines. One bead on each rod (the leftmost one) is divided from the others by a bar (the reckoning bar). This single bead is called go-dama and four others are ichi-damas. Each rod is responsible for representing a single digit from 0 to 9. We can obtain the value of a digit by following simple algorithm: Set the value of a digit equal to 0. If the go-dama is shifted to the right, add 5. Add the number of ichi-damas shifted to the left.
Thus, the upper rod on the picture shows digit 0, the middle one shows digit 2 and the lower one shows 7. We will consider the top rod to represent the last decimal digit of a number, so the picture shows number 720.
Write the program that prints the way Soroban shows the given number n.
-----Input-----
The first line contains a single integer n (0 ≤ n < 10^9).
-----Output-----
Print the description of the decimal digits of number n from the last one to the first one (as mentioned on the picture in the statement), one per line. Print the beads as large English letters 'O', rod pieces as character '-' and the reckoning bar as '|'. Print as many rods, as many digits are in the decimal representation of number n without leading zeroes. We can assume that number 0 has no leading zeroes.
-----Examples-----
Input
2
Output
O-|OO-OO
Input
13
Output
O-|OOO-O
O-|O-OOO
Input
720
Output
O-|-OOOO
O-|OO-OO
-O|OO-OO
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[100], [2], [3], [8], [1111], [3000]], \"outputs\": [[null], [7], [0], [7], [9], [5]]}", "source": "taco"}
|
Looking at consecutive powers of `2`, starting with `2^1`:
`2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, ...`
Note that out of all the digits `0-9`, the last one ever to appear is `7`. It only shows up for the first time in the number `32768 (= 2^15)`.
So let us define LAST DIGIT TO APPEAR as the last digit to be written down when writing down all the powers of `n`, starting with `n^1`.
## Your task
You'll be given a positive integer ```1 =< n <= 10000```, and must return the last digit to appear, as an integer.
If for any reason there are digits which never appear in the sequence of powers, return `None`/`nil`.
Please note: The Last digit to appear can be in the same number as the penultimate one. For example for `n = 8`, the last digit to appear is `7`, although `3` appears slightly before it, in the same number:
`8, 64, 512, 4096, 32768, ...`
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4181 6765\\n\", \"416445288135075809 416445288135075809\\n\", \"964542760623675601 965233603018687501\\n\", \"2 1000000000000000000\\n\", \"999999999999999999 999999999999999998\\n\", \"498454011879264 806515533049393\\n\", \"1 1000000000000000000\\n\", \"519421744863260201 572972909476222789\\n\", \"977367244641009653 977367244641009653\\n\", \"242 100\\n\", \"1 3\\n\", \"395130552422107969 382562323268297483\\n\", \"27961 931\\n\", \"701408733 433494437\\n\", \"152139002499 367296043199\\n\", \"540431588408227541 540431588408227541\\n\", \"453151988636162147 474019690903735841\\n\", \"402725448165665593 481342602240996343\\n\", \"1000000000000000000 999999999999999999\\n\", \"1000000000000000000 1000000000000000000\\n\", \"1000000000000000000 1\\n\", \"567036128564717939 510505130335113937\\n\", \"5 3\\n\", \"423506197818989927 442863139846534733\\n\", \"957591654759084713 981022104435698593\\n\", \"832040 514229\\n\", \"127601 6382601\\n\", \"507769900974602687 547261784951014891\\n\", \"5702887 9227465\\n\", \"616274828435574301 10268395600356301\\n\", \"2 1\\n\", \"408962762283480959 444443583457646111\\n\", \"956722026041 591286729879\\n\", \"8 5\\n\", \"412177780967225699 432177937877609093\\n\", \"585026192452577797 570146946822492493\\n\", \"529495319593227313 631186172547690847\\n\", \"976540997167958951 969335176443917693\\n\", \"5 2\\n\", \"410218934960967047 378596216455001869\\n\", \"46368 75025\\n\", \"25220791 839761\\n\", \"963716517445592213 976351630941239591\\n\", \"568679881256193737 513570106829158157\\n\", \"1000100020001 100010001\\n\", \"420196140727489673 679891637638612258\\n\", \"97 101\\n\", \"55 89\\n\", \"10808314049304201 270039182096201\\n\", \"610 987\\n\", \"962890278562476113 969978235623119279\\n\", \"4181 12239\\n\", \"416445288135075809 563314488195882934\\n\", \"936870169534750540 965233603018687501\\n\", \"2 1000000000001000000\\n\", \"999999999999999999 486717039931737871\\n\", \"186874666488720 806515533049393\\n\", \"519421744863260201 991781214200367251\\n\", \"977367244641009653 732330312112008696\\n\", \"635802456424329389 382562323268297483\\n\", \"17557 931\\n\", \"701408733 203117851\\n\", \"81208341629 367296043199\\n\", \"226627794080227858 540431588408227541\\n\", \"453151988636162147 764249597669282045\\n\", \"293722622982448634 481342602240996343\\n\", \"1000000000010000000 1\\n\", \"567036128564717939 906021951406663252\\n\", \"423506197818989927 756946102346578281\\n\", \"754352360359572269 981022104435698593\\n\", \"6038 514229\\n\", \"127601 9869981\\n\", \"679750036208196398 547261784951014891\\n\", \"6830183 9227465\\n\", \"616274828435574301 867339007556327\\n\", \"123759270458662931 444443583457646111\\n\", \"956722026041 206611925956\\n\", \"3 5\\n\", \"497175297938326506 432177937877609093\\n\", \"585026192452577797 650068960466418230\\n\", \"897127940498560767 631186172547690847\\n\", \"730217125016805768 969335176443917693\\n\", \"62950647016727756 378596216455001869\\n\", \"22958164 839761\\n\", \"963716517445592213 1860181315322498763\\n\", \"568679881256193737 780878906056714154\\n\", \"1676317493168 100010001\\n\", \"587356350727522011 679891637638612258\\n\", \"97 001\\n\", \"55 107\\n\", \"760 987\\n\", \"962890278562476113 1822396991792306136\\n\", \"1 2\\n\", \"4181 23344\\n\", \"186874666488720 1483263391357787\\n\", \"519421744863260201 1273226458168407248\\n\", \"675683766904283032 382562323268297483\\n\", \"23934 931\\n\", \"1397825118 203117851\\n\", \"132378233262 367296043199\\n\", \"857876679897362492 764249597669282045\\n\", \"361472044211165723 481342602240996343\\n\", \"1100000000010000000 1\\n\", \"567036128564717939 258007274120909150\\n\", \"85492415990246642 756946102346578281\\n\", \"472221311484944782 981022104435698593\\n\", \"2 1000000000000000010\\n\", \"35 100\\n\", \"1000000100000000000 999999999999999999\\n\", \"1000000000000000000 1000000000100000000\\n\", \"46368 52232\\n\", \"14260723811854408 270039182096201\\n\", \"3 3\\n\", \"128572318315696646 563314488195882934\\n\", \"936870169534750540 840255662248736780\\n\", \"999999999999999999 94720554785727112\\n\", \"2 1010000000000000010\\n\", \"158177332839047721 732330312112008696\\n\", \"226627794080227858 991328683609933862\\n\", \"1000000110000000000 999999999999999999\\n\", \"3 2\\n\", \"2 2\\n\", \"1 4\\n\"], \"outputs\": [\"1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A\", \"Impossible\", \"1B1396A5B2A4B2A2B1A18B4A1B1A1B2A3B3A1B10A2B3A1B3A1B5A1B1A1B2A10B3A9B1A1B3A2B\", \"Impossible\", \"1A999999999999999997B\", \"1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B\", \"999999999999999999B\", \"1B9A1B2A3B21A1B1A21B2A1B2A12B1A4B1A1B5A160B4A1B1A138B1A1B9A4B3A2B6A\", \"Impossible\", \"Impossible\", \"2B\", \"Impossible\", \"30A30B30A\", \"1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B\", \"2B2A2B2A2B2A2B2A2B2A2B2A2B2A2B2A2B2A2B2A2B2A2B2A2B2A2B2A2B2A\", \"Impossible\", \"1B21A1B2A1B1A16B1A1B1A4B300A1B4A1B11A47B1A6B8A1B1A1B1A2B2A5B3A2B1A7B1A5B1A\", \"1B5A8B6A2B2A1B20A3B9A5B2A1B4A5B2A4B1A268B9A4B1A1B4A3B2A2B1A2B1A1B3A\", \"1A999999999999999998B\", \"Impossible\", \"999999999999999999A\", \"1A9B32A1B2A1B368A1B1A1B2A4B1A1B23A14B21A5B1A1B2A4B1A1B3A1B1A1B3A1B5A1B1A9B\", \"1A1B1A\", \"1B21A1B7A4B76A1B3A2B82A1B18A4B1A13B1A3B6A1B1A2B1A22B1A3B2A1B1A2B27A\", \"1B40A1B6A1B1A1B68A1B18A2B3A1B2A2B2A1B1A4B1A3B2A1B12A3B604A5B1A1B39A1B1A\", \"1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B\", \"50B50A50B50A\", \"Impossible\", \"1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B\", \"60A60B60A60B60A60B60A60B60A60B\", \"1A\", \"1B11A1B1A9B253A1B5A22B6A1B11A4B3A2B1A1B4A1B13A2B4A1B50A1B6A1B5A3B\", \"1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A\", \"1A1B1A1B\", \"1B20A1B1A1B1A3B1A58B1A4B1A13B206A2B2A5B5A22B3A45B1A7B5A1B1A6B1A1B\", \"1A38B3A7B23A2B1A1B1A8B2A1B5A117B2A1B1A2B12A3B10A5B3A2B3A11B2A1B7A\", \"1B5A4B1A4B1A76B3A2B11A3B7A5B1A1B2A2B7A2B2A8B5A3B143A1B3A8B1A5B1A\", \"1A134B1A1B11A3B26A2B3A1B1A2B22A1B3A3B1A1B66A63B36A2B1A13B5A3B\", \"2A1B\", \"Impossible\", \"1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B\", \"30A30B30A30B30A\", \"1B76A3B1A1B1A52B1A6B2A7B35A1B1A2B17A5B5A4B5A9B3A2B13A1B2A3B1A7B\", \"1A9B3A7B2A3B1A1B1A2B3A2B1A3B2A82B1A7B2A14B2A1B1A4B5A3B2A1B9A1B2A1B4A1B3A1B3A2B\", \"10000A10000B10000A\", \"1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B1A1B\", \"1B24A3B\", \"1B1A1B1A1B1A1B1A1B\", \"40A40B40A40B40A40B40A40B40A40B\", \"1B1A1B1A1B1A1B1A1B1A1B1A1B1A\", \"1B135A1B5A1B1A1B1A2B1A1B3A4B2A1B2A2B1A5B3A1B2A2B2A1B2A1B3A2B67A1B1A6B3A1B14A1B3A19B\", \"2B1A12B1A3B18A1B2A\\n\", \"1B2A1B5A12B1A2B1A37B3A1B23A1B2A1B2A1B2A3B33A1B5A7B2A2B1A2B2A3B40A3B1A1B12A\\n\", \"1B33A32B2A1B7A1B4A1B1A2B1A1B1A1B1A6B4A2B1A2B11A1B4A3B1A2B12A3B1A1B2A2B1A1B5A1B1A44B\\n\", \"Impossible\\n\", \"2A18B3A8B1A3B16A6B4139A4B1A2B1A8B5A5B2A1B1A2B2A1B1A4B9A5B1A1B2A\\n\", \"4B3A6B135A1B1A4B1A1B4A4B1A4B3A3B2A1B7A1B42A1B1A10B113A\\n\", \"1B1A10B27A10B6A2B1A1B3A2B6A20B11A3B2A1B1A2B1A10B25A2B2A1B1A1B1A1B75A3B1A\\n\", \"1A2B1A87B7A1B5A1B1A1B12A4B2A1B7A1B4A1B1A5B2A27B1A3B6A4B1A4B1A2B1A10B1A4B3A1B3A\\n\", \"1A1B1A1B22A1B13A4B3A8B3A2B11A2B3A1B2A3B3A3B9A1B1A7B2A6B2A107B1A30B2A\\n\", \"18A1B6A18B1A5B\\n\", \"3A2B4A1B5A2B1A2B9A1B19A1B25A2B31A\\n\", \"4B1A1B10A2B2A1B3A1B1A1B2A2B4A3B1A62B1A198B1A25B\\n\", \"2B2A1B1A2B116A1B1A2B3A4B3A1B44A7B1A3B5A1B2A2B6A53B1A3B2A1B58A1B2A9B\\n\", \"1B1A2B5A3B1A3B1A8B1A3B1A5B3A1B20A6B2A38B3A4B1A28B3A3B1A1B5A7B90A2B\\n\", \"1B1A1B1A3B3A5B1A27B1A7B1A4B1A1B5A4B6A6B1A2B1A2B13A1B5A12B1A14B1A1B10A1B2A1B1A14B\\n\", \"1000000000009999999A\\n\", \"1B1A1B2A17B1A20B4A1B4A2B2A2B1A4B2A1B1A1B1A1B2A1B2A90B6A7B1A4B1A60B1A2B1A5B1A2B1A2B\\n\", \"1B1A3B1A2B2A1B3A1B12A1B5A1B5A2B1A1B2A4B6A1B1A1B28A1B5A1B19A2B4A11B1A1B4A5B16A7B\\n\", \"1B3A3B20A2B2A1B2A2B1A4B1A13B1A1B5A2B1A4B6A3B6A17B1A2B3A1B2A1B1A1B5A3B2A2B12A2B4A\\n\", \"85B6A22B1A2B2A1B1A1B\\n\", \"77B2A1B5A1B6A2B5A2B11A1B1A\\n\", \"1A4B7A1B1A1B8A2B1A1B2A1B3A2B1379A1B5A8B4A14B6A2B54A1B4A1B3A1B2A1B3A1B1A\\n\", \"1B2A1B5A1B1A1B2A4B10A1B2A3B1A1B1A12B1A\\n\", \"710A1B1A6B1A1B1A1B1A1B1A1B3A1B8A1B5A1B1A1B3A2B2A1B1A6B2A2B1A2B2A1B13A1B4A1B11A3B2A1B7A\\n\", \"3B1A1B2A4B7A56B1A5B70A8B1A7B30A2B1A1B1A1B1A3B1A13B4A1B1A4B3A1B1A3B2A3B\\n\", \"4A1B1A1B2A2B2A4B1A2B1A2B1A2B1A10B49A1B1207A4B1A3B\\n\", \"1B1A1B\\n\", \"1A6B1A1B1A5B1A2B7A1B1A1B1A1B9A1B4A3B79A1B20A6B2A9B2A2B9A1B1A2B9A1B1A2B2A15B\\n\", \"1B8A1B180A3B7A1B1A6B1A2B1A1B1A1B2A2B1A2B1A1B1A10B1A43B10A3B9A5B1A7B30A1B1A\\n\", \"1A2B2A1B2A9B2A1B1A3B2A8B2A67B2A2B1A1B5A2B7A1B1A2B5A2B3A1B4A70B3A3B1A24B1A\\n\", \"1B3A18B1A1B2A3B2A6B5A3B1A3B1A3B4A9B1A28B1A7B2A6B1A24B1A1B16A6B2A1B3A1B4A1B\\n\", \"6B70A1B1A4B1A13B1A1B12A2B4A1B1A1B1A3B1A11B1A1B17A5B18A2B5A2B1A2B2A1B1A2B15A\\n\", \"27A2B1A19B5A563B2A1B\\n\", \"1B1A13B3A32B1A9B1A4B4A1B4A2B4A8B2A3B2A4B3A1B3A3B3A1B3A3B2A2B1A1B8A3B8A1B7A\\n\", \"1B2A1B2A8B25A50B2A8B15A2B5A3B14A1B7A3B1A16B1A1B1A1B136A1B1A59B\\n\", \"16761A2B179A1B9A5B1A5B1A3B6A1B1A1B3A1B\\n\", \"1B6A2B1A7B4A12B1A2B4A7B1A1B5A2B1A2B1A1B4A6B1A1B100A3B1A1B7A2B5A6B4A2B1A1B2A1B\\n\", \"96A\\n\", \"1B1A17B2A\\n\", \"1B3A2B1A6B1A8B\\n\", \"1B1A8B3A5B2A1B8A1B14A1B1A2B3A5B10A1B1A1B1A1B46A7B10A1B2A3B5A4B5A1B3A1B13A1B3A\\n\", \"1B\\n\", \"5B1A1B2A2B347A\\n\", \"7B1A14B1A12B1A1B19A1B1A1B3A1B1A1B1A1B2A1B2A3B5A1B1A3B14A1B1A3B3A1B8A1B1A5B1A1B\\n\", \"2B2A4B1A1B1A2B7A1B1A4B2A1B2A2B2A1B1A25B1A42B3A1B8A1B4A9B2A26B2A4B1A19B2A1B1A1B2A\\n\", \"1A1B3A3B1A1B1A1B5A2B2A7B3A4B1A6B1A1B2A3B8A1B1A2B21A13B1A17B1A20B125A2B3A1B\\n\", \"25A1B2A2B2A1B2A1B4A1B\\n\", \"6A1B7A2B6A3B4A1B8A1B4A2B1A2B32A1B6A\\n\", \"2B1A3B2A3B2A3B2A1B7A1B90A1B1A6B1A12B1A1B1A2B1A2B2A13B\\n\", \"1A8B6A6B1A4B1A38B6A2B8A3B1A1B2A3B6A2B1A6B1A1B1A2B4A2B62A1B2A39B1A2B4A\\n\", \"1B3A64B2A3B3A1B2A6B1A7B1A1B140A2B4A4B1A1B17A1B1A5B1A2B1A1B62A11B1A5B1A\\n\", \"1100000000009999999A\\n\", \"2A5B17A1B1A2B15A3B11A4B3A4B1A2B18A1B18A1B3A7B1A1B1A1B8A1B2A1B20A1B8A2B2A1B\\n\", \"8B1A5B1A5B1A1B4A1B4A2B25A6B1A5B1A30B5A7B1A1B1A1B3A1B14A1B7A3B1A1B10A1B1A2B1A5B\\n\", \"2B12A1B10A22B2A1B2A2B3A147B29A3B1A2B1A1B4A1B8A1B1A9B1A2B9A1B2A1B1A3B4A1B3A\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"Impossible\\n\", \"1A1B\", \"Impossible\", \"3B\"]}", "source": "taco"}
|
Alice and Bob decided to eat some fruit. In the kitchen they found a large bag of oranges and apples. Alice immediately took an orange for herself, Bob took an apple. To make the process of sharing the remaining fruit more fun, the friends decided to play a game. They put multiple cards and on each one they wrote a letter, either 'A', or the letter 'B'. Then they began to remove the cards one by one from left to right, every time they removed a card with the letter 'A', Alice gave Bob all the fruits she had at that moment and took out of the bag as many apples and as many oranges as she had before. Thus the number of oranges and apples Alice had, did not change. If the card had written letter 'B', then Bob did the same, that is, he gave Alice all the fruit that he had, and took from the bag the same set of fruit. After the last card way removed, all the fruit in the bag were over.
You know how many oranges and apples was in the bag at first. Your task is to find any sequence of cards that Alice and Bob could have played with.
Input
The first line of the input contains two integers, x, y (1 ≤ x, y ≤ 1018, xy > 1) — the number of oranges and apples that were initially in the bag.
Output
Print any sequence of cards that would meet the problem conditions as a compressed string of characters 'A' and 'B. That means that you need to replace the segments of identical consecutive characters by the number of repetitions of the characters and the actual character. For example, string AAABAABBB should be replaced by string 3A1B2A3B, but cannot be replaced by 2A1A1B2A3B or by 3AB2A3B. See the samples for clarifications of the output format. The string that you print should consist of at most 106 characters. It is guaranteed that if the answer exists, its compressed representation exists, consisting of at most 106 characters. If there are several possible answers, you are allowed to print any of them.
If the sequence of cards that meet the problem statement does not not exist, print a single word Impossible.
Examples
Input
1 4
Output
3B
Input
2 2
Output
Impossible
Input
3 2
Output
1A1B
Note
In the first sample, if the row contained three cards with letter 'B', then Bob should give one apple to Alice three times. So, in the end of the game Alice has one orange and three apples, and Bob has one apple, in total it is one orange and four apples.
In second sample, there is no answer since one card is not enough for game to finish, and two cards will produce at least three apples or three oranges.
In the third sample, cards contain letters 'AB', so after removing the first card Bob has one orange and one apple, and after removal of second card Alice has two oranges and one apple. So, in total it is three oranges and two apples.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"1 100\\n79\\n\", \"50 3\\n33 7 96 30 68 37 44 50 100 71 12 100 72 43 17 75 59 96 16 34 25 3 90 45 7 55 92 59 30 25 96 23 40 41 95 99 93 79 89 11 76 60 4 100 75 14 37 39 87 47\\n\", \"100 10\\n3 114 77 78 105 87 6 122 141 100 75 118 64 18 88 37 109 72 31 101 36 10 62 18 52 17 149 115 22 150 138 48 46 42 104 8 63 21 117 58 87 80 7 131 125 118 67 13 144 43 59 67 74 13 124 77 86 148 107 11 51 9 87 52 147 22 7 22 143 12 121 123 17 35 33 87 91 140 92 38 106 10 66 26 40 100 121 42 134 127 116 111 52 139 88 30 28 106 49 19\\n\", \"44 4\\n58 39 131 78 129 35 93 61 123 25 40 9 50 9 93 66 99 115 28 45 32 31 137 114 140 85 138 12 98 53 75 29 15 17 74 87 36 62 43 132 37 103 116 142\\n\", \"18 6\\n22 8 11 27 37 19 18 49 47 18 15 25 8 3 5 11 32 47\\n\", \"111 11\\n20 83 25 94 8 2 29 54 36 74 63 85 27 40 84 3 86 83 18 88 92 82 87 38 47 54 14 37 46 51 61 24 17 19 81 50 24 75 97 65 59 100 7 42 83 79 57 19 24 66 57 63 73 5 30 38 60 53 1 99 99 40 41 64 12 39 75 69 70 79 79 73 93 46 69 32 58 31 60 11 32 24 11 11 8 35 3 46 35 17 42 72 7 22 67 84 41 52 96 89 46 36 95 69 1 79 97 81 47 91 90\\n\", \"50 5\\n1 2 4 6 8 9 10 11 14 16 19 20 23 24 26 29 30 33 36 38 41 44 45 46 48 51 53 56 59 61 62 64 65 66 68 70 72 73 76 79 80 83 86 87 90 93 96 97 98 101\\n\", \"30 4\\n4 6 10 15 20 22 27 29 30 31 34 38 39 42 47 50 54 58 62 63 65 66 68 73 74 79 83 86 91 95\\n\", \"5 2\\n3 13 33 45 53\\n\", \"10 2\\n69 4 43 36 33 27 59 5 86 55\\n\", \"11 4\\n28 31 12 19 3 26 15 25 47 19 6\\n\", \"100 100\\n1 1 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100\\n\", \"100 10\\n1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100\\n\", \"19 3\\n43 47 64 91 51 88 22 66 48 48 92 91 16 1 2 38 38 91 91\\n\", \"10 3\\n12 21 26 32 40 51 56 57 67 75\\n\", \"2 2\\n50 100\\n\", \"50 3\\n33 7 96 30 68 37 44 50 100 71 12 100 72 43 17 75 59 96 16 34 25 3 90 45 7 55 92 59 30 25 96 23 40 41 95 99 93 97 89 11 76 60 4 100 75 14 37 39 87 47\\n\", \"100 10\\n3 114 77 78 105 87 6 122 141 100 75 118 64 18 88 37 109 72 31 101 36 10 62 18 52 17 149 115 22 150 138 48 46 42 104 8 63 21 117 58 87 80 7 131 125 118 67 13 144 43 59 67 74 13 124 77 86 148 107 11 51 9 87 52 147 22 7 22 143 12 121 123 17 35 33 87 91 140 92 38 106 10 54 26 40 100 121 42 134 127 116 111 52 139 88 30 28 106 49 19\\n\", \"18 6\\n22 8 11 27 37 13 18 49 47 18 15 25 8 3 5 11 32 47\\n\", \"111 11\\n20 83 25 94 8 2 29 54 36 74 63 85 27 40 84 3 23 83 18 88 92 82 87 38 47 54 14 37 46 51 61 24 17 19 81 50 24 75 97 65 59 100 7 42 83 79 57 19 24 66 57 63 73 5 30 38 60 53 1 99 99 40 41 64 12 39 75 69 70 79 79 73 93 46 69 32 58 31 60 11 32 24 11 11 8 35 3 46 35 17 42 72 7 22 67 84 41 52 96 89 46 36 95 69 1 79 97 81 47 91 90\\n\", \"30 4\\n4 6 10 15 39 22 27 29 30 31 34 38 39 42 47 50 54 58 62 63 65 66 68 73 74 79 83 86 91 95\\n\", \"5 2\\n3 13 33 45 27\\n\", \"10 2\\n114 4 43 36 33 27 59 5 86 55\\n\", \"100 100\\n1 1 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 18 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100\\n\", \"100 10\\n1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 132 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100\\n\", \"19 6\\n43 47 64 91 51 88 22 66 48 48 92 91 16 1 2 38 38 91 91\\n\", \"4 1\\n32 100 33 1\\n\", \"100 10\\n3 114 77 78 105 87 6 122 141 100 75 118 64 18 88 37 109 72 31 101 36 10 62 18 52 17 149 115 22 150 138 48 46 42 104 8 63 21 117 58 87 80 7 131 125 118 67 13 144 43 59 67 74 13 124 77 86 148 107 11 51 9 87 52 147 22 7 22 143 12 121 123 17 35 33 12 91 140 92 38 106 10 54 26 40 100 121 42 134 127 116 111 52 139 88 30 28 106 49 19\\n\", \"100 10\\n1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 132 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100\\n\", \"19 6\\n43 47 64 91 51 88 22 66 48 48 92 45 16 1 2 38 38 91 91\\n\", \"111 11\\n20 83 25 94 8 2 29 54 33 74 63 85 27 40 84 3 23 83 18 88 92 82 87 38 47 54 14 37 15 51 61 24 17 19 81 50 24 75 97 65 59 100 7 42 83 79 57 19 24 66 57 63 73 5 30 38 60 53 1 99 99 40 41 64 12 39 75 69 70 79 79 73 93 46 69 32 58 31 60 11 32 24 11 11 8 35 3 46 35 17 42 72 7 22 67 84 41 52 96 89 46 36 95 69 1 79 97 81 47 91 90\\n\", \"100 10\\n1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 132 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 64 100\\n\", \"44 4\\n58 39 131 78 129 35 93 61 123 25 40 9 50 9 93 66 99 115 28 45 32 31 137 114 140 85 3 12 98 53 75 29 15 17 74 87 36 62 43 132 37 103 116 142\\n\", \"11 4\\n28 31 12 19 3 1 15 25 47 19 6\\n\", \"10 3\\n12 21 4 32 40 51 56 57 67 75\\n\", \"14 5\\n48 19 6 9 50 20 3 42 38 43 9 21 44 6\\n\", \"50 3\\n33 7 96 30 68 37 44 50 100 71 12 100 72 43 17 75 59 96 16 34 25 3 90 45 7 55 92 59 30 25 96 23 40 41 95 99 93 97 89 11 76 76 4 100 75 14 37 39 87 47\\n\", \"44 4\\n58 39 131 78 129 35 93 61 123 25 40 9 50 9 93 66 99 115 28 45 32 31 137 114 140 101 3 12 98 53 75 29 15 17 74 87 36 62 43 132 37 103 116 142\\n\", \"18 6\\n22 8 11 27 37 13 18 49 47 18 15 25 7 3 5 11 32 47\\n\", \"111 11\\n20 83 25 94 8 2 29 54 33 74 63 85 27 40 84 3 23 83 18 88 92 82 87 38 47 54 14 37 46 51 61 24 17 19 81 50 24 75 97 65 59 100 7 42 83 79 57 19 24 66 57 63 73 5 30 38 60 53 1 99 99 40 41 64 12 39 75 69 70 79 79 73 93 46 69 32 58 31 60 11 32 24 11 11 8 35 3 46 35 17 42 72 7 22 67 84 41 52 96 89 46 36 95 69 1 79 97 81 47 91 90\\n\", \"30 4\\n4 6 10 15 39 22 27 29 30 31 34 38 39 42 47 50 54 58 62 63 65 66 68 73 74 79 83 86 26 95\\n\", \"5 2\\n6 13 33 45 27\\n\", \"10 2\\n125 4 43 36 33 27 59 5 86 55\\n\", \"100 100\\n1 1 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 18 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 6 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100\\n\", \"10 3\\n12 21 4 32 40 51 103 57 67 75\\n\", \"14 5\\n48 19 6 9 50 20 3 42 38 43 9 21 44 11\\n\", \"50 3\\n33 7 96 30 68 37 44 50 100 71 12 100 72 43 17 75 59 96 16 34 25 1 90 45 7 55 92 59 30 25 96 23 40 41 95 99 93 97 89 11 76 76 4 100 75 14 37 39 87 47\\n\", \"100 10\\n3 114 77 78 105 87 6 122 141 100 75 118 64 18 88 37 109 72 31 101 36 10 62 18 52 17 149 115 22 150 138 48 46 42 104 8 63 21 117 58 87 80 7 131 125 118 67 13 144 43 59 67 74 13 124 77 86 148 107 22 51 9 87 52 147 22 7 22 143 12 121 123 17 35 33 12 91 140 92 38 106 10 54 26 40 100 121 42 134 127 116 111 52 139 88 30 28 106 49 19\\n\", \"44 4\\n58 39 131 78 129 68 93 61 123 25 40 9 50 9 93 66 99 115 28 45 32 31 137 114 140 101 3 12 98 53 75 29 15 17 74 87 36 62 43 132 37 103 116 142\\n\", \"18 6\\n22 8 11 27 37 13 18 49 47 18 15 25 1 3 5 11 32 47\\n\", \"30 4\\n4 6 10 15 39 22 27 29 30 31 34 38 39 42 47 50 56 58 62 63 65 66 68 73 74 79 83 86 26 95\\n\", \"5 2\\n6 10 33 45 27\\n\", \"10 2\\n125 4 43 36 33 27 59 1 86 55\\n\", \"100 100\\n1 1 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 18 26 27 28 29 30 8 32 33 34 35 36 37 38 39 40 41 42 43 44 6 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100\\n\", \"19 6\\n43 47 63 91 51 88 22 66 48 48 92 45 16 1 2 38 38 91 91\\n\", \"10 3\\n12 21 1 32 40 51 103 57 67 75\\n\", \"14 5\\n48 19 6 9 50 20 3 42 38 43 9 20 44 11\\n\", \"50 3\\n33 7 96 30 68 37 44 50 100 71 12 100 72 43 17 75 59 96 16 34 25 1 90 45 7 55 92 59 30 25 96 23 40 41 95 99 93 97 89 11 76 76 4 101 75 14 37 39 87 47\\n\", \"44 4\\n58 39 131 78 129 68 93 61 137 25 40 9 50 9 93 66 99 115 28 45 32 31 137 114 140 101 3 12 98 53 75 29 15 17 74 87 36 62 43 132 37 103 116 142\\n\", \"18 6\\n22 8 11 27 37 5 18 49 47 18 15 25 1 3 5 11 32 47\\n\", \"111 11\\n20 83 25 94 8 2 29 54 33 74 63 85 27 40 84 2 23 83 18 88 92 82 87 38 47 54 14 37 15 51 61 24 17 19 81 50 24 75 97 65 59 100 7 42 83 79 57 19 24 66 57 63 73 5 30 38 60 53 1 99 99 40 41 64 12 39 75 69 70 79 79 73 93 46 69 32 58 31 60 11 32 24 11 11 8 35 3 46 35 17 42 72 7 22 67 84 41 52 96 89 46 36 95 69 1 79 97 81 47 91 90\\n\", \"30 4\\n4 6 10 15 39 22 27 29 48 31 34 38 39 42 47 50 56 58 62 63 65 66 68 73 74 79 83 86 26 95\\n\", \"5 2\\n6 3 33 45 27\\n\", \"100 100\\n1 1 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 18 26 27 28 29 30 8 32 33 34 35 36 37 38 39 40 41 42 43 44 6 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 80 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100\\n\", \"100 10\\n1 2 3 4 5 6 7 8 9 10 11 15 13 14 15 16 17 18 19 20 2 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 132 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 64 100\\n\", \"19 6\\n43 47 63 91 51 88 22 66 48 48 92 27 16 1 2 38 38 91 91\\n\", \"10 3\\n12 20 1 32 40 51 103 57 67 75\\n\", \"14 5\\n48 19 6 9 50 20 3 62 38 43 9 20 44 11\\n\", \"50 3\\n33 7 96 30 68 37 44 50 100 71 12 100 72 43 17 75 59 96 16 34 25 1 90 45 7 55 92 59 30 34 96 23 40 41 95 99 93 97 89 11 76 76 4 101 75 14 37 39 87 47\\n\", \"44 4\\n58 39 131 78 129 68 93 61 137 25 40 9 50 9 93 66 99 115 28 45 32 31 137 114 140 101 3 12 98 53 75 29 15 21 74 87 36 62 43 132 37 103 116 142\\n\", \"18 6\\n22 8 11 27 37 5 18 49 47 18 15 25 2 3 5 11 32 47\\n\", \"111 11\\n20 83 25 94 8 2 3 54 33 74 63 85 27 40 84 2 23 83 18 88 92 82 87 38 47 54 14 37 15 51 61 24 17 19 81 50 24 75 97 65 59 100 7 42 83 79 57 19 24 66 57 63 73 5 30 38 60 53 1 99 99 40 41 64 12 39 75 69 70 79 79 73 93 46 69 32 58 31 60 11 32 24 11 11 8 35 3 46 35 17 42 72 7 22 67 84 41 52 96 89 46 36 95 69 1 79 97 81 47 91 90\\n\", \"14 5\\n48 19 6 9 50 20 3 42 38 43 36 21 44 6\\n\", \"2 2\\n49 100\\n\", \"4 2\\n32 100 33 1\\n\"], \"outputs\": [\"0\\n\", \"24\\n\", \"59\\n\", \"25\\n\", \"2\\n\", \"50\\n\", \"35\\n\", \"16\\n\", \"0\\n\", \"4\\n\", \"3\\n\", \"98\\n\", \"90\\n\", \"10\\n\", \"3\\n\", \"0\\n\", \"24\\n\", \"59\\n\", \"3\\n\", \"48\\n\", \"16\\n\", \"0\\n\", \"5\\n\", \"98\\n\", \"90\\n\", \"7\\n\", \"1\\n\", \"58\\n\", \"89\\n\", \"6\\n\", \"47\\n\", \"88\\n\", \"24\\n\", \"0\\n\", \"5\\n\", \"5\\n\", \"24\\n\", \"24\\n\", \"3\\n\", \"48\\n\", \"16\\n\", \"0\\n\", \"5\\n\", \"98\\n\", \"6\\n\", \"5\\n\", \"24\\n\", \"58\\n\", \"24\\n\", \"3\\n\", \"16\\n\", \"0\\n\", \"5\\n\", \"98\\n\", \"6\\n\", \"6\\n\", \"5\\n\", \"24\\n\", \"24\\n\", \"6\\n\", \"47\\n\", \"16\\n\", \"0\\n\", \"98\\n\", \"88\\n\", \"6\\n\", \"6\\n\", \"5\\n\", \"24\\n\", \"24\\n\", \"6\\n\", \"47\\n\", \"5\\n\", \"1\\n\", \"2\\n\"]}", "source": "taco"}
|
Vasya likes taking part in Codeforces contests. When a round is over, Vasya follows all submissions in the system testing tab.
There are n solutions, the i-th of them should be tested on a_i tests, testing one solution on one test takes 1 second. The solutions are judged in the order from 1 to n. There are k testing processes which test solutions simultaneously. Each of them can test at most one solution at a time.
At any time moment t when some testing process is not judging any solution, it takes the first solution from the queue and tests it on each test in increasing order of the test ids. Let this solution have id i, then it is being tested on the first test from time moment t till time moment t + 1, then on the second test till time moment t + 2 and so on. This solution is fully tested at time moment t + a_i, and after that the testing process immediately starts testing another solution.
Consider some time moment, let there be exactly m fully tested solutions by this moment. There is a caption "System testing: d%" on the page with solutions, where d is calculated as
$$$d = round\left(100⋅m/n\right),$$$
where round(x) = ⌊{x + 0.5}⌋ is a function which maps every real to the nearest integer.
Vasya calls a submission interesting if there is a time moment (possibly, non-integer) when the solution is being tested on some test q, and the caption says "System testing: q%". Find the number of interesting solutions.
Please note that in case when multiple processes attempt to take the first submission from the queue at the same moment (for instance, at the initial moment), the order they take the solutions does not matter.
Input
The first line contains two positive integers n and k (1 ≤ n ≤ 1000, 1 ≤ k ≤ 100) standing for the number of submissions and the number of testing processes respectively.
The second line contains n positive integers a_1, a_2, …, a_n (1 ≤ a_i ≤ 150), where a_i is equal to the number of tests the i-th submission is to be run on.
Output
Output the only integer — the number of interesting submissions.
Examples
Input
2 2
49 100
Output
1
Input
4 2
32 100 33 1
Output
2
Input
14 5
48 19 6 9 50 20 3 42 38 43 36 21 44 6
Output
5
Note
Consider the first example. At time moment 0 both solutions start testing. At time moment 49 the first solution is fully tested, so at time moment 49.5 the second solution is being tested on the test 50, and the caption says "System testing: 50%" (because there is one fully tested solution out of two). So, the second solution is interesting.
Consider the second example. At time moment 0 the first and the second solutions start testing. At time moment 32 the first solution is fully tested, the third solution starts testing, the caption says "System testing: 25%". At time moment 32 + 24.5 = 56.5 the third solutions is being tested on test 25, the caption is still the same, thus this solution is interesting. After that the third solution is fully tested at time moment 32 + 33 = 65, the fourth solution is fully tested at time moment 65 + 1 = 66. The captions becomes "System testing: 75%", and at time moment 74.5 the second solution is being tested on test 75. So, this solution is also interesting. Overall, there are two interesting solutions.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.375
|
{"tests": "{\"inputs\": [[7, 3], [11, 19], [40, 3], [14, 2], [100, 1], [1, 300], [2, 300], [5, 300], [7, 300], [300, 300]], \"outputs\": [[4], [10], [28], [13], [100], [1], [1], [1], [7], [265]]}", "source": "taco"}
|
In this kata you have to correctly return who is the "survivor", ie: the last element of a Josephus permutation.
Basically you have to assume that n people are put into a circle and that they are eliminated in steps of k elements, like this:
```
josephus_survivor(7,3) => means 7 people in a circle;
one every 3 is eliminated until one remains
[1,2,3,4,5,6,7] - initial sequence
[1,2,4,5,6,7] => 3 is counted out
[1,2,4,5,7] => 6 is counted out
[1,4,5,7] => 2 is counted out
[1,4,5] => 7 is counted out
[1,4] => 5 is counted out
[4] => 1 counted out, 4 is the last element - the survivor!
```
The above link about the "base" kata description will give you a more thorough insight about the origin of this kind of permutation, but basically that's all that there is to know to solve this kata.
**Notes and tips:** using the solution to the other kata to check your function may be helpful, but as much larger numbers will be used, using an array/list to compute the number of the survivor may be too slow; you may assume that both n and k will always be >=1.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[\"lamppu\"], [\"lamppu sofia\"], [\"silly game\"], [\"aeiou\"], [\"xyz lamppu\"], [\"\"], [\"lAmppU\"], [\"silly grrr\"]], \"outputs\": [[\"komppu-lantti\"], [\"komppu-lantti kofia-sontti\"], [\"kolly-sintti kome-gantti\"], [\"koeiou-antti\"], [\"koz-xyntti komppu-lantti\"], [\"\"], [\"komppU-lAntti\"], [\"kolly-sintti grrr\"]]}", "source": "taco"}
|
Kontti language is a finnish word play game.
You add `-kontti` to the end of each word and then swap their characters until and including the first vowel ("aeiouy");
For example the word `tame` becomes `kome-tantti`; `fruity` becomes `koity-fruntti` and so on.
If no vowel is present, the word stays the same.
Write a string method that turns a sentence into kontti language!
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"6\\n(?????\\n\", \"10\\n(???(???(?\\n\", \"4\\n))((\\n\", \"6\\n))??((\\n\", \"10\\n((?()??())\\n\", \"10\\n())))()(((\\n\", \"6\\n(?((??\\n\", \"18\\n?(?(?(?(?(?(?(?(??\\n\", \"18\\n??)??))?)?)???))))\\n\", \"18\\n((?((((???(??(????\\n\", \"2\\n??\\n\", \"1\\n?\\n\", \"4\\n????\\n\", \"6\\n((((??\\n\", \"6\\n??))))\\n\", \"8\\n(((?(?(?\\n\", \"30\\n?()????(????)???)??)?????????(\\n\", \"30\\n???(??)??(??)?(??()(?????(?)?(\\n\", \"30\\n((?(?????()?(?)???????)?)??(??\\n\", \"30\\n((??)?)???(????(????)???????((\\n\", \"30\\n???(???(?????(?????????((?????\\n\", \"300\\n)?)???????(?????????)??)??)?)??)??()???)??)??????????(?)???(?????)????????????????????)?????)???(???????)?????)?)??????????????))????(?)??????)???)?(?????????)?))???)???????????????))))???)???)????????(?())?????)????(??))???)????)??????)???)?)?????))???)??(?)??????????)??????)??????)????)?)?)??)??)?\\n\", \"300\\n???)??????(?)(????????((????????)????)????????????????)??)??)(?))???))??)?)(?)?????(???)?)?))?????????))??????????)???????????)??)?(????(????))?????))???(????)?)????)???)??))?(?(?))?)???)?????)??????????????)??)???)(????)????????)?)??))???)?)?)???((??)??(?)??)?????(??)?????????????????(?(??)????(?)(\\n\", \"300\\n????(??)?(???(???????????)?(??(?(????)????)????(??????????????????)?????(???)(??????????(???(?(?(((?)????(??)(??(?????)?)???????)??????(??)(??)???????(?()???????)???)???????????????))?(????)?(????(???)???????????)????????????)???)??(???????)???)??(?())????((?)??)(????)?)?)???(?????????(??????)(?)??(\\n\", \"300\\n??????(??????(???)??(???????)??????)((??????(???(??)())?(???????)???????????((??(??(??(?)???)(????)??(??(?(??(????????()?????(????(?(??(?(?????)??(????(????(??(??(????((??)(??(??????????????????(????????(????(?(???????(??(????(???)?(???????)?)??(?????((??(??(??????????()?????(??????)??(((??(????????\\n\", \"300\\n?(??(??????????(?????????(????(????)???????????((??????((??(???(?(((????(??((?((((??(?(?????(???????????)??)????????(?(????????(?(??(???????(???(???((???()?????(???????(?????(?????((?????????(??(????(????????((?????????((???????)?()????????(??????)???????????(??(??????(?(???????((????(?(?(??????(???\\n\", \"1\\n(\\n\", \"1\\n)\\n\", \"2\\n((\\n\", \"3\\n(()\\n\", \"3\\n))(\\n\", \"3\\n())\\n\", \"4\\n()()\\n\", \"4\\n((((\\n\", \"4\\n))))\\n\", \"4\\n)()(\\n\", \"4\\n(())\\n\", \"4\\n)??(\\n\", \"4\\n(??)\\n\", \"4\\n?)??\\n\", \"4\\n??(?\\n\", \"6\\n((?())\\n\", \"30\\n((??)?)???(????(????)???????((\\n\", \"6\\n))??((\\n\", \"4\\n??(?\\n\", \"6\\n((?())\\n\", \"300\\n)?)???????(?????????)??)??)?)??)??()???)??)??????????(?)???(?????)????????????????????)?????)???(???????)?????)?)??????????????))????(?)??????)???)?(?????????)?))???)???????????????))))???)???)????????(?())?????)????(??))???)????)??????)???)?)?????))???)??(?)??????????)??????)??????)????)?)?)??)??)?\\n\", \"4\\n?)??\\n\", \"300\\n????(??)?(???(???????????)?(??(?(????)????)????(??????????????????)?????(???)(??????????(???(?(?(((?)????(??)(??(?????)?)???????)??????(??)(??)???????(?()???????)???)???????????????))?(????)?(????(???)???????????)????????????)???)??(???????)???)??(?())????((?)??)(????)?)?)???(?????????(??????)(?)??(\\n\", \"30\\n???(???(?????(?????????((?????\\n\", \"18\\n??)??))?)?)???))))\\n\", \"6\\n(?((??\\n\", \"3\\n(()\\n\", \"6\\n(?????\\n\", \"4\\n)??(\\n\", \"30\\n???(??)??(??)?(??()(?????(?)?(\\n\", \"4\\n))((\\n\", \"4\\n()()\\n\", \"4\\n((((\\n\", \"4\\n????\\n\", \"1\\n)\\n\", \"3\\n))(\\n\", \"6\\n??))))\\n\", \"1\\n?\\n\", \"3\\n())\\n\", \"4\\n(())\\n\", \"4\\n(??)\\n\", \"8\\n(((?(?(?\\n\", \"1\\n(\\n\", \"300\\n???)??????(?)(????????((????????)????)????????????????)??)??)(?))???))??)?)(?)?????(???)?)?))?????????))??????????)???????????)??)?(????(????))?????))???(????)?)????)???)??))?(?(?))?)???)?????)??????????????)??)???)(????)????????)?)??))???)?)?)???((??)??(?)??)?????(??)?????????????????(?(??)????(?)(\\n\", \"30\\n((?(?????()?(?)???????)?)??(??\\n\", \"18\\n((?((((???(??(????\\n\", \"10\\n((?()??())\\n\", \"18\\n?(?(?(?(?(?(?(?(??\\n\", \"10\\n())))()(((\\n\", \"2\\n??\\n\", \"30\\n?()????(????)???)??)?????????(\\n\", \"4\\n))))\\n\", \"2\\n((\\n\", \"4\\n)()(\\n\", \"6\\n((((??\\n\", \"300\\n?(??(??????????(?????????(????(????)???????????((??????((??(???(?(((????(??((?((((??(?(?????(???????????)??)????????(?(????????(?(??(???????(???(???((???()?????(???????(?????(?????((?????????(??(????(????????((?????????((???????)?()????????(??????)???????????(??(??????(?(???????((????(?(?(??????(???\\n\", \"300\\n??????(??????(???)??(???????)??????)((??????(???(??)())?(???????)???????????((??(??(??(?)???)(????)??(??(?(??(????????()?????(????(?(??(?(?????)??(????(????(??(??(????((??)(??(??????????????????(????????(????(?(???????(??(????(???)?(???????)?)??(?????((??(??(??????????()?????(??????)??(((??(????????\\n\", \"30\\n((???????)????(????(???)?)??((\\n\", \"300\\n(??)?()??????(?????????(???)?)?)????()??)?((????))(?(??)???)???????(??)???)????????????)???????????)???(????(?)????(?))???????????????)???)???????)(?(???????)??()??(??????)???????)?)?????(??()??(????)?(((?(?(???(??????????()???(?????)??????????????????(????)????)????(?(??(?)???????????(???(?)??(????\\n\", \"300\\n??????(??????(???)??((??????)??????)((??????(???(??)())?(???????)???????????((??(??(??(?)???)?????)??(??(?(??(????????()?????(????(?(??(?(?????)??(????(????(??(??(????((??)(??(??????????????????(????????(????(?(???????(??(????(???)?(???????)?)??(?????((??(??(??????????()?????(??????)??(((??(????????\\n\", \"2\\n()\\n\", \"300\\n????????(??(((??)??????(?????)(??????????(??(??((?????(??)?)???????(?)???(????(??(???????(?(????(????????(??????????????????(??()??((????(??(??(????(????(??)?????(?(??(?(????(?????)(????????(??(?(??(??)?????)???)?(??(??(??((???????????)???????(?))()??(???(??????(()??????)??????((??)???(??????(??????\\n\", \"10\\n?(?(?(????\\n\", \"300\\n????????(??(((??)??????)?????)(??????????(??(??((?????(??)?)???????(?)???(????(??(???????(?(????(????????(??????????????????(??()??((????(??(??(????(????(??)?????(?(??(?(????(?????)(????????(??(?(??(??)?????)???)?(??(??(??((???????????)???????(?))()??(???(??????(()??????)??????((??)???(??????(??????\\n\", \"300\\n?(??(??????????(?????????(????(????)???????????((??????()??(???(?(((????(??((?((((??(?(?????(???????????)??????)????(?(????????(?(??(???????(???(???((???()?????(???????(?????(?????((?????????(??(????(????????((??????????)???????)?()????????(??????)(??????????(??(??????(?(???????((????(?(?(??????(???\\n\", \"4\\n??)?\\n\", \"300\\n(??)?()??????(?????????(???)?)?)????()??)?((????))(?(??)???)???????(??)???)????????????)???????)???)???(????(?)????(?))???????????????)???)???????)(?(???????)??()??(??????)?????????)?????(??()??(????)?(((?(?(???(??????????()???(?????)??????????????????(????)????)????(?(??(?)???????????(???(?)??(????\\n\", \"6\\n)?)?((\\n\", \"6\\n))(?((\\n\", \"300\\n)?)???????(?????????)??)??)?)??)??()???)??)??????????(?)???(?????)????????????????????)?????)???(?)?????)?????)?)??????????????))????(?)??????)???)?(?????????)?))???)???????????????))))???)???)????????(?(?)?????)????(??))???)????)??????)???)?)?????))???)??(?)??????????)??????)??????)????)?)?)??)??)?\\n\", \"18\\n??)??))?)?)???)))(\\n\", \"3\\n)((\\n\", \"4\\n()((\\n\", \"4\\n))()\\n\", \"3\\n))'\\n\", \"6\\n))))??\\n\", \"3\\n'))\\n\", \"4\\n())(\\n\", \"8\\n?(?(?(((\\n\", \"300\\n???)??????(?)(????????((????????)????)????????????????)??)??)(?))???))??)?)(?)?????(???)?)?))?????????))??????????)???????????)??)?(????(????))?????))???(????)?)????)???)??()?(?(?))?)???)?????)??????????????)??)???)(????)????????)?)??))???)?)?)???((??)??(?)??)?????(??)?????????????????(?(??)????(?)(\\n\", \"30\\n??(??)?)???????)?(?)(?????(?((\\n\", \"10\\n((?()??)()\\n\", \"10\\n()())()()(\\n\", \"2\\n)(\\n\", \"4\\n(()(\\n\", \"300\\n???(??????(?(?(????((???????(?(??????(??(???????????)??????(????????)(?)???????((?????????((????????(????(??(?????????((?????(?????(???????(?????)(???((???(???(???????(??(?(????????(?(????????)??)???????????(?????(?(??((((?((??(????(((?(???(??((??????((???????????)????(????(?????????(??????????(??(?\\n\", \"6\\n?????(\\n\", \"10\\n?(???(???(\\n\", \"300\\n?)??)??)?)?)????)??????)??????)??????????)?(??)???))?????)?)???)??????)????)???))??(????)?????)?(?(????????)???)???))))???????????????)???))?)?????????(?)???)??????)?(????))??????????????)?)?????)?????)?(???)?????)????????????????????)?????(???)?(??????????)??)???)(??)??)?)??)??)?????????(???????)?)\\n\", \"300\\n????(??)?(???(???????????)?(??(?(????)????)????(??????????????????)?????(???)(??????????(???(?(?(((?)????(??)(??(?????)?)???????)??????(??)(??)???????(?()???????)???)???????????????))?(????)?(????(???)???????????)????????????)???)??(???????)???)??(?())????((?)??)(????)?)?)???(?????????(??????))?)??(\\n\", \"18\\n??)??))?)?)??)))?(\\n\", \"3\\n()(\\n\", \"3\\n)')\\n\", \"6\\n)??)))\\n\", \"3\\n&))\\n\", \"10\\n)()??)(?((\\n\", \"10\\n()()())()(\\n\", \"300\\n???(??????(?(?(????((???????(?(??????(??(??????????()??????(????????)(?)???????(??????????((????????(????(??(?????????((?????(?????(???????(?????)(???((???(???(???????(??(?(????????(?(????????)??)???????????(?????(?(??((((?((??(????(((?(???(??((??????((???????????)????(????(?????????(??????????(??(?\\n\", \"300\\n?)??)??)???)????)??????)??????)??????????)?(??)???))?????)?)???)??????)????)???))??(????)?????)?(?(????????)???)???))))???????????????)???))?)?????????(?)???)??????)?(????))??????????????)?)?????)?????)?(???)?????)????????????????????)?????(???)?(???)??????)??)???)(??)??)?)??)??)?????????(???????)?)\\n\", \"3\\n*)(\\n\", \"3\\n&)*\\n\", \"10\\n(??()(?)()\\n\", \"10\\n()()())())\\n\", \"300\\n???(??????(?(?(????((???????(?(??????(??(??????????()??????(????????)(?)???????(??????????((????????(????(??(?????????((?????(?????(???????(?????)(???((???(???(???????(??(?(????????(?(????)??????)???????????(?????(?(??((((?((??(????(((?(???(??((??????((???????????)????(????(?????????(??????????(??(?\\n\", \"3\\n()*\\n\", \"3\\n)&*\\n\", \"10\\n((?()(?)?)\\n\", \"300\\n???(??????(?(?(????((???????(?(??????(??(??????????()??????(????????)(?)???????)??????????((????????(????(??(?????????((?????(?????(???????(?????)(???((???(???(???????(??(?(????????(?(????)??????)???????????(?????(?(??((((?((??(????(((?(???(??((??????((???????????)????(????(?????????(??????????(??(?\\n\", \"300\\n??????(?(??(((??)??????)?????)(??????????(??(??((?????(??)?)???????(?)???(????(??(?????????(????(????????(??????????????????(??()??((????(??(??(????(????(??)?????(?(??(?(????(?????)(????????(??(?(??(??)?????)???)?(??(??(??((???????????)???????(?))()??(???(??????(()??????)??????((??)???(??????(??????\\n\", \"3\\n')*\\n\", \"10\\n)?)?()(?((\\n\", \"300\\n???(??????(?(?(????((???????(?(??????(??(??????????()??????(????????)(?)???????)??????????((????????(????(??(?????????((?????(?????(???????(?????)(???((???(???(???????(??(?(????????(?(????)??????)???????????(?????(?(??((((?((??(????(((?(???(??)(??????((???????????)????(????(?????????(??????????(??(?\\n\", \"3\\n)'*\\n\", \"30\\n(((?)?)???(?????????)???????((\\n\", \"6\\n))?((?\\n\", \"6\\n((?(()\\n\", \"18\\n)?)??))?)?)???)?))\\n\", \"3\\n**(\\n\", \"4\\n)?(?\\n\", \"4\\n)(()\\n\", \"4\\n()))\\n\", \"4\\n)(((\\n\", \"3\\n)()\\n\", \"3\\n)))\\n\", \"4\\n)())\\n\", \"8\\n)((?(?(?\\n\", \"30\\n??(??)?)?????????(?)(???)?(?((\\n\", \"18\\n????(??(???((((?((\\n\", \"10\\n))(??)(?((\\n\", \"10\\n)))))()(((\\n\", \"30\\n(?????????)??)???)????(????)(?\\n\", \"4\\n((()\\n\", \"6\\n????(?\\n\", \"6\\n)??)((\\n\", \"6\\n)((?((\\n\", \"300\\n)?)???????(?????????)??)??)?)??)??()???)??)??????????(?)???(?????)????????????????????)?????)???(?)?????)?????)?)??????????????))????(?)??????)???)?(?????????)?))???)???????????????))))???)???)????????(?(?)?????)????(??))???)????)??????)???)?)?????)(???)??(?)??????????)??????)??????)????)?)?)??)??)?\\n\", \"18\\n()))???)?)?))??)??\\n\", \"3\\n)('\\n\", \"6\\n)))??)\\n\", \"3\\n&)(\\n\", \"300\\n???)??????(?)(????????((????)???)????)????????????????)??)??)(?))???))??)?)(?)?????(???)?)?))?????????)???????????)???????????)??)?(????(????))?????))???(????)?)????)???)??()?(?(?))?)???)?????)??????????????)??)???)(????)????????)?)??))???)?)?)???((??)??(?)??)?????(??)?????????????????(?(??)????(?)(\\n\", \"10\\n())))((()(\\n\", \"300\\n?)??)??)?)?)????)??????)??????)?????)????)?(??)???))?????)?)???)??????)????)???))??(????)?????)?(?(????????)???)???)))????????????????)???))?)?????????(?)???)??????)?(????))??????????????)?)?????)?????)?(???)?????)????????????????????)?????(???)?(??????????)??)???)(??)??)?)??)??)?????????(???????)?)\\n\", \"18\\n??)??)(?)?)??)))?(\\n\", \"3\\n(((\\n\", \"3\\n)'(\\n\", \"6\\n(?????\\n\", \"10\\n(???(???(?\\n\"], \"outputs\": [\"((()))\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"(((()))())\\n\", \":(\\n\", \":(\\n\", \"(()()()()()()()())\\n\", \"(()(())()()((())))\\n\", \"((((((()))())())))\\n\", \"()\\n\", \":(\\n\", \"(())\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"(((((((((()((()()))))))))))())\\n\", \":(\\n\", \"(((((((((((()()))))))))(()))))\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"((((((((((((((((()(((((((((()(((((()((((((((((((((()())((((((((()((((((((((((((((((((((()((()((((()(((((((((((((((((((()((((((((()()())()())))))))())))())))())())())))(()))())())))))))))))))))))())))))))())))()()))))))())())))()))))())))))))))))()))))(())())())))))))))())))))()))))))))((())())))))))\\n\", \"((((((((((((((((((((((((((((((((((()(((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((()(()((((((((((((())))))()())()))))))()))()))(()))())))))()))))))()))))()))))(()))))))))())())))())))))))(()))))))))(()))))))))()))))))))())))))))))))))))))())())))))()()))))))(())))()()())))))()))\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"(())\\n\", \":(\\n\", \"(())\\n\", \":(\\n\", \":(\\n\", \"(()())\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"(()())\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"(((((((((((()()))))))))(()))))\\n\", \"(()(())()()((())))\\n\", \":(\\n\", \":(\\n\", \"((()))\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"(())\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"(())\\n\", \"(())\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"(((((((((()((()()))))))))))())\\n\", \"((((((()))())())))\\n\", \"(((()))())\\n\", \"(()()()()()()()())\\n\", \":(\\n\", \"()\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"((((((((((((((((((((((((((((((((((()(((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((()(()((((((((((((())))))()())()))))))()))()))(()))())))))()))))))()))))()))))(()))))))))())())))())))))))(()))))))))(()))))))))()))))))))())))))))))))))))))())())))))()()))))))(())))()()())))))()))\\n\", \"((((((((((((((((()(((((((((()(((((()((((((((((((((()())((((((((()((((((((((((((((((((((()((()((((()(((((((((((((((((((()((((((((()()())()())))))))())))())))())())())))(()))())())))))))))))))))))())))))))())))()()))))))())())))()))))())))))))))))()))))(())())())))))))))())))))()))))))))((())())))))))\\n\", \":(\\n\", \"((()(()(((((((((((((((((((()()()((((()(()((((((())((((()((()(((((((((()((()(((((((((((()((((((((((()(((((((((()(((((())((((((((((((((()((()((((((()(((()))))))))()))())))))))))))))))))))))())()))())))))((()()()))())))))))))())))())))))))))))))))))))))))())))))))))))))()())()))))))))))))()))())))())))\\n\", \"((((((((((((((((()(((((((((()(((((()((((((((((((((()())((((((((()((((((((((((((((((((((()((()((((()(((((((((((((((((((()((((((((()()())()())))))))())))())))())())())))(()))())())))))))))))))))))())))))))())))()()))))))())())))()))))())))))))))))()))))(())())())))))))))())))))()))))))))((())())))))))\\n\", \"()\\n\", \"(((((((((((((((()(((((((((((()((((((((((((((((((((((((((()()((((((((()((((((((((((((((((((((((((((((((((((((((((((((((((()))())()))(())))())())())))())))())))))))()())()())))())))))())))))))())()())())))))))))))))())())())(()))))))))))))))))))()))()))()))())))))(())))))))))))))(())))))())))))())))))\\n\", \"(((()())))\\n\", \"(((((((((((((((()(((((()((((()((((((((((((((((((((((((((()()((((((((()(((((((((((((((((((((((((((((((((((((((((((((((((((())())()))(())))())())())))())))())))))))()())()())))())))))())))))))())()())())))))))))))))())())())(()))))))))))))))))))()))()))()))())))))(())))))))))))))(())))))())))))())))))\\n\", \"((((((((((((((((((((((((((((((((((()(((((((((((((((((((()((((((((((((((((((((((((((((((((((((((((((((((()(((((()((((((((((())))()())()))))))()))()))(()))())))))()))))))()))))()))))(()))))))))())())))())))))))(())))))))))))))))))))()))))))))()))))))())))))))))())())))))()()))))))(())))()()())))))()))\\n\", \"(())\\n\", \"((()(()(((((((((((((((((((()()()((((()(()((((((())((((()((()(((((((((()((()(((((((((((()((((((()((()(((((((((()(((((())((((((((((((((()((()((((((()((((())))))))()))())))))))))))))))))))))())()))())))))((()()()))())))))))))())))())))))))))))))))))))))))())))))))))))))()())()))))))))))))()))())))())))\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"(((()())))\\n\", \":(\\n\", \"(((((((((((((((()(((((()((((()((((((((((((((((((((((((((()()((((((((()(((((((((((((((((((((((((((((((((((((((((((((((((((())())()))(())))())())())))())))())))))))()())()())))())))))())))))))())()())())))))))))))))())())())(()))))))))))))))))))()))()))()))())))))(())))))))))))))(())))))())))))())))))\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \":(\\n\", \"((()))\\n\", \":(\\n\"]}", "source": "taco"}
|
Serval soon said goodbye to Japari kindergarten, and began his life in Japari Primary School.
In his favorite math class, the teacher taught him the following interesting definitions.
A parenthesis sequence is a string, containing only characters "(" and ")".
A correct parenthesis sequence is a parenthesis sequence that can be transformed into a correct arithmetic expression by inserting characters "1" and "+" between the original characters of the sequence. For example, parenthesis sequences "()()", "(())" are correct (the resulting expressions are: "(1+1)+(1+1)", "((1+1)+1)"), while ")(" and ")" are not. Note that the empty string is a correct parenthesis sequence by definition.
We define that $|s|$ as the length of string $s$. A strict prefix $s[1\dots l]$ $(1\leq l< |s|)$ of a string $s = s_1s_2\dots s_{|s|}$ is string $s_1s_2\dots s_l$. Note that the empty string and the whole string are not strict prefixes of any string by the definition.
Having learned these definitions, he comes up with a new problem. He writes down a string $s$ containing only characters "(", ")" and "?". And what he is going to do, is to replace each of the "?" in $s$ independently by one of "(" and ")" to make all strict prefixes of the new sequence not a correct parenthesis sequence, while the new sequence should be a correct parenthesis sequence.
After all, he is just a primary school student so this problem is too hard for him to solve. As his best friend, can you help him to replace the question marks? If there are many solutions, any of them is acceptable.
-----Input-----
The first line contains a single integer $|s|$ ($1\leq |s|\leq 3 \cdot 10^5$), the length of the string.
The second line contains a string $s$, containing only "(", ")" and "?".
-----Output-----
A single line contains a string representing the answer.
If there are many solutions, any of them is acceptable.
If there is no answer, print a single line containing ":(" (without the quotes).
-----Examples-----
Input
6
(?????
Output
(()())
Input
10
(???(???(?
Output
:(
-----Note-----
It can be proved that there is no solution for the second sample, so print ":(".
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [[\"I am applying for the role of Base Manager on Titan.\", 60, true], [\"I am looking to relocate to the vicinity of Saturn for family reasons.\", 70, true], [\"As Deputy Base Manager on Phobos for five Martian years, I have significant relevant experience.\", 90, false], [\"A challenging career moment came with the rapid depletion of water supplies on Phobos.\", 80, false], [\"But, as I pointed out, anyone complaining about standing downwind was lying. There was no wind.\", 75, true], [\"I have no notice period on Phobos. I can start immediately.\", 50, true]], \"outputs\": [[[true, \"I am applying for the role of Base Manager on Titan.\"]], [[true, \"I am looking to relocate to the vicinity of Saturn for family reasons.\"]], [[true, \"AsDeputyBaseManageronPhobosforfiveMartianyears,Ihavesignificantrelevantexperience.\"]], [[true, \"AchallengingcareermomentcamewiththerapiddepletionofwatersuppliesonPhobos.\"]], [[false, \"But, as I pointed out, anyone complaining about standing downwind was lying\"]], [[false, \"I have no notice period on Phobos. I can start imm\"]]]}", "source": "taco"}
|
Cara is applying for several different jobs.
The online application forms ask her to respond within a specific character count.
Cara needs to check that her answers fit into the character limit.
Annoyingly, some application forms count spaces as a character, and some don't.
Your challenge:
Write Cara a function `charCheck()` with the arguments:
- `"text"`: a string containing Cara's answer for the question
- `"max"`: a number equal to the maximum number of characters allowed in the answer
- `"spaces"`: a boolean which is `True` if spaces are included in the character count and `False` if they are not
The function `charCheck()` should return an array: `[True, "Answer"]` , where `"Answer"` is equal to the original text, if Cara's answer is short enough.
If her answer `"text"` is too long, return an array: `[False, "Answer"]`.
The second element should be the original `"text"` string truncated to the length of the limit.
When the `"spaces"` argument is `False`, you should remove the spaces from the `"Answer"`.
For example:
- `charCheck("Cara Hertz", 10, True)` should return `[ True, "Cara Hertz" ]`
- `charCheck("Cara Hertz", 9, False)` should return `[ True, "CaraHertz" ]`
- `charCheck("Cara Hertz", 5, True)` should return `[ False, "Cara " ]`
- `charCheck("Cara Hertz", 5, False)` should return `[ False, "CaraH" ]`
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"10 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 7 10\\n5 9 8\\n6 10 5\\n8 10 5\", \"4 2\\n1 2 2\\n3 4 2\", \"10 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 7 10\\n5 9 8\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 7 10\\n3 9 8\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 13\\n1 3 5\\n4 7 10\\n3 9 1\\n6 10 5\\n5 10 5\", \"4 2\\n1 2 1\\n1 4 2\", \"10 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 7 10\\n5 9 8\\n9 10 5\\n8 10 5\", \"10 7\\n1 5 18\\n3 4 13\\n1 3 5\\n4 7 10\\n3 9 1\\n6 10 5\\n5 10 0\", \"10 7\\n1 5 18\\n3 4 10\\n1 3 5\\n4 7 10\\n3 9 1\\n1 10 5\\n5 10 5\", \"10 7\\n1 7 31\\n3 4 0\\n1 3 5\\n4 5 10\\n3 9 1\\n6 10 1\\n5 10 7\", \"10 7\\n1 5 31\\n3 4 8\\n1 3 5\\n4 7 10\\n4 9 8\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 36\\n3 4 10\\n2 3 5\\n4 5 10\\n3 9 1\\n6 10 5\\n5 10 5\", \"3 1\\n1 3 4\\n6 0 0\", \"10 7\\n1 5 18\\n3 4 14\\n1 3 5\\n4 7 10\\n1 9 8\\n6 10 5\\n5 10 10\", \"10 7\\n1 5 36\\n3 4 10\\n2 3 5\\n4 5 10\\n3 9 1\\n6 10 5\\n8 10 5\", \"10 7\\n2 5 30\\n3 4 13\\n1 3 4\\n4 7 10\\n3 9 8\\n6 10 5\\n5 16 5\", \"10 7\\n1 5 18\\n3 4 14\\n1 2 5\\n4 7 10\\n4 9 1\\n6 10 5\\n8 10 5\", \"10 7\\n1 5 18\\n3 4 8\\n1 5 5\\n4 7 10\\n5 9 8\\n6 10 5\\n8 10 3\", \"4 2\\n1 4 1\\n3 4 2\", \"10 7\\n2 5 18\\n3 4 8\\n1 3 5\\n4 6 10\\n5 9 8\\n9 10 5\\n8 10 5\", \"10 7\\n1 9 18\\n3 4 13\\n1 3 8\\n4 7 10\\n3 9 1\\n6 10 5\\n5 10 0\", \"1 2\\n2 2 2\\n3 3 2\", \"10 7\\n1 3 31\\n3 4 0\\n1 4 5\\n4 5 10\\n6 9 1\\n6 10 1\\n5 10 7\", \"10 7\\n1 5 18\\n3 4 13\\n1 3 5\\n4 7 10\\n2 9 0\\n6 10 6\\n5 10 5\", \"10 7\\n1 5 31\\n3 4 8\\n1 3 5\\n4 7 1\\n4 9 8\\n6 10 5\\n5 10 9\", \"14 7\\n1 9 18\\n3 4 10\\n1 3 1\\n4 5 10\\n3 9 0\\n6 14 2\\n5 10 5\", \"10 7\\n1 9 18\\n3 4 13\\n1 6 8\\n4 7 10\\n3 9 1\\n6 10 5\\n5 10 0\", \"10 7\\n1 5 18\\n3 4 10\\n1 2 5\\n4 7 10\\n3 9 1\\n6 10 6\\n5 10 10\", \"10 7\\n1 5 18\\n2 4 8\\n1 3 5\\n3 7 9\\n5 9 8\\n9 10 5\\n8 10 5\", \"10 7\\n1 5 26\\n3 4 14\\n1 2 5\\n4 7 10\\n3 9 1\\n6 10 5\\n3 7 5\", \"10 7\\n1 8 18\\n3 4 8\\n1 3 5\\n4 7 12\\n5 9 8\\n6 10 3\\n8 10 5\", \"10 7\\n1 5 18\\n3 4 13\\n1 3 10\\n3 7 10\\n3 9 8\\n2 10 5\\n5 16 5\", \"10 7\\n1 5 36\\n3 4 10\\n2 3 5\\n4 5 18\\n5 9 0\\n7 10 5\\n5 10 2\", \"10 7\\n1 5 26\\n3 4 14\\n1 2 5\\n1 7 13\\n3 9 1\\n6 10 7\\n3 7 9\", \"14 7\\n2 4 18\\n1 4 10\\n2 3 1\\n4 10 10\\n3 9 -1\\n6 14 5\\n5 10 0\", \"4 2\\n1 2 2\\n3 4 0\", \"3 2\\n1 2 2\\n3 4 0\", \"10 7\\n1 5 18\\n3 4 13\\n1 3 5\\n4 7 10\\n3 9 8\\n6 10 5\\n5 10 5\", \"3 2\\n1 2 2\\n6 4 0\", \"10 7\\n1 5 18\\n3 4 10\\n1 3 5\\n4 7 10\\n3 9 1\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 10\\n1 3 5\\n4 5 10\\n3 9 1\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 10\\n1 3 5\\n4 5 10\\n3 9 1\\n6 14 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 10\\n1 3 5\\n4 8 10\\n3 9 1\\n6 14 5\\n5 10 5\", \"4 2\\n1 2 2\\n3 6 2\", \"3 2\\n1 2 4\\n6 4 0\", \"10 7\\n1 5 18\\n3 4 10\\n1 3 5\\n4 5 10\\n3 9 1\\n6 10 5\\n5 10 7\", \"10 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 6 10\\n5 9 8\\n9 10 5\\n8 10 5\", \"4 2\\n1 2 2\\n3 3 2\", \"3 2\\n1 2 4\\n6 0 0\", \"10 7\\n1 9 18\\n3 4 13\\n1 3 5\\n4 7 10\\n3 9 1\\n6 10 5\\n5 10 0\", \"10 7\\n1 5 31\\n3 4 10\\n1 3 5\\n4 5 10\\n3 9 1\\n6 10 5\\n5 10 7\", \"10 7\\n1 7 31\\n3 4 10\\n1 3 5\\n4 5 10\\n3 9 1\\n6 10 5\\n5 10 7\", \"10 7\\n1 7 31\\n3 4 0\\n1 3 5\\n4 5 10\\n3 9 1\\n6 10 5\\n5 10 7\", \"10 7\\n1 3 31\\n3 4 0\\n1 3 5\\n4 5 10\\n3 9 1\\n6 10 1\\n5 10 7\", \"10 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 7 10\\n5 9 8\\n8 10 5\\n8 10 5\", \"4 2\\n2 2 2\\n3 4 2\", \"10 7\\n1 5 18\\n3 4 14\\n1 3 5\\n4 7 10\\n5 9 8\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 31\\n3 4 8\\n1 3 5\\n4 7 10\\n3 9 8\\n6 10 5\\n5 10 5\", \"3 2\\n1 3 2\\n3 4 0\", \"10 7\\n1 5 18\\n3 4 13\\n1 3 5\\n4 7 10\\n3 9 8\\n6 10 5\\n5 16 5\", \"10 7\\n1 5 18\\n3 4 13\\n1 3 5\\n4 7 10\\n2 9 1\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 10\\n1 2 5\\n4 7 10\\n3 9 1\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 10\\n2 3 5\\n4 5 10\\n3 9 1\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 10\\n1 3 1\\n4 5 10\\n3 9 1\\n6 14 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 7 9\\n5 9 8\\n9 10 5\\n8 10 5\", \"3 2\\n1 2 5\\n6 4 0\", \"10 7\\n1 5 18\\n3 4 14\\n1 3 5\\n4 7 10\\n3 9 1\\n1 10 5\\n5 10 5\", \"4 2\\n2 2 2\\n3 3 2\", \"3 1\\n1 2 4\\n6 0 0\", \"10 7\\n1 7 31\\n3 4 10\\n1 3 5\\n4 5 10\\n3 9 1\\n1 10 5\\n5 10 7\", \"10 7\\n1 7 31\\n3 4 0\\n1 3 5\\n4 5 10\\n3 9 1\\n6 10 5\\n5 0 7\", \"10 7\\n1 3 31\\n3 4 0\\n1 4 5\\n4 5 10\\n3 9 1\\n6 10 1\\n5 10 7\", \"15 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 7 10\\n5 9 8\\n8 10 5\\n8 10 5\", \"10 7\\n1 5 18\\n3 4 14\\n1 3 5\\n4 7 10\\n5 9 8\\n6 10 5\\n5 10 10\", \"3 2\\n1 3 2\\n6 4 0\", \"10 7\\n2 5 18\\n3 4 13\\n1 3 5\\n4 7 10\\n3 9 8\\n6 10 5\\n5 16 5\", \"10 7\\n1 5 18\\n3 4 13\\n1 3 5\\n4 7 10\\n2 9 1\\n6 10 6\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 14\\n1 2 5\\n4 7 10\\n3 9 1\\n6 10 5\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 10\\n1 3 1\\n4 5 10\\n3 9 0\\n6 14 5\\n5 10 5\", \"4 2\\n2 2 2\\n3 2 2\", \"10 7\\n1 3 31\\n3 4 0\\n1 4 3\\n4 5 10\\n3 9 1\\n6 10 1\\n5 10 7\", \"15 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 7 10\\n5 9 8\\n8 10 2\\n8 10 5\", \"10 7\\n1 5 31\\n3 4 8\\n1 3 5\\n4 7 10\\n4 9 8\\n6 10 5\\n5 10 9\", \"3 2\\n1 3 2\\n6 6 0\", \"10 7\\n2 5 30\\n3 4 13\\n1 3 5\\n4 7 10\\n3 9 8\\n6 10 5\\n5 16 5\", \"10 7\\n1 5 18\\n3 4 13\\n1 3 5\\n4 7 9\\n2 9 1\\n6 10 6\\n5 10 5\", \"10 7\\n1 5 18\\n3 4 14\\n1 2 5\\n4 7 10\\n4 9 1\\n6 10 5\\n5 10 5\", \"10 7\\n1 9 18\\n3 4 10\\n1 3 1\\n4 5 10\\n3 9 0\\n6 14 5\\n5 10 5\", \"3 2\\n2 2 2\\n3 2 2\", \"3 1\\n1 3 4\\n7 0 0\", \"10 7\\n1 3 31\\n3 4 0\\n1 4 3\\n4 5 10\\n3 9 1\\n6 10 1\\n5 15 7\", \"15 7\\n1 5 18\\n3 4 10\\n1 3 5\\n4 7 10\\n5 9 8\\n8 10 2\\n8 10 5\", \"10 7\\n1 5 18\\n3 4 14\\n1 3 5\\n4 7 10\\n1 9 8\\n6 10 5\\n5 6 10\", \"15 7\\n1 5 18\\n3 4 13\\n1 3 5\\n4 7 9\\n2 9 1\\n6 10 6\\n5 10 5\", \"10 7\\n1 5 36\\n3 4 10\\n2 3 9\\n4 5 10\\n3 9 1\\n6 10 5\\n8 10 5\", \"14 7\\n1 9 18\\n3 4 10\\n1 3 1\\n4 5 10\\n3 9 0\\n6 14 5\\n5 10 5\", \"3 2\\n3 2 2\\n3 2 2\", \"3 1\\n1 3 4\\n7 0 -1\", \"10 7\\n1 3 31\\n3 4 0\\n1 4 3\\n4 5 10\\n3 9 1\\n6 10 1\\n5 15 4\", \"15 7\\n1 5 15\\n3 4 10\\n1 3 5\\n4 7 10\\n5 9 8\\n8 10 2\\n8 10 5\", \"4 3\\n1 3 2\\n2 4 3\\n1 4 6\", \"10 7\\n1 5 18\\n3 4 8\\n1 3 5\\n4 7 10\\n5 9 8\\n6 10 5\\n8 10 3\", \"4 2\\n1 2 1\\n3 4 2\"], \"outputs\": [\"28\\n\", \"-1\\n\", \"23\\n\", \"18\\n\", \"11\\n\", \"2\\n\", \"31\\n\", \"6\\n\", \"5\\n\", \"7\\n\", \"26\\n\", \"41\\n\", \"4\\n\", \"13\\n\", \"42\\n\", \"17\\n\", \"24\\n\", \"16\\n\", \"1\\n\", \"36\\n\", \"9\\n\", \"0\\n\", \"22\\n\", \"10\\n\", \"19\\n\", \"3\\n\", \"8\\n\", \"25\\n\", \"27\\n\", \"32\\n\", \"21\\n\", \"15\\n\", \"38\\n\", \"20\\n\", \"14\\n\", \"-1\\n\", \"-1\\n\", \"18\\n\", \"-1\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"-1\\n\", \"-1\\n\", \"11\\n\", \"31\\n\", \"-1\\n\", \"-1\\n\", \"6\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"7\\n\", \"31\\n\", \"-1\\n\", \"23\\n\", \"18\\n\", \"2\\n\", \"18\\n\", \"11\\n\", \"23\\n\", \"23\\n\", \"7\\n\", \"31\\n\", \"-1\\n\", \"5\\n\", \"-1\\n\", \"-1\\n\", \"5\\n\", \"11\\n\", \"7\\n\", \"-1\\n\", \"28\\n\", \"2\\n\", \"18\\n\", \"11\\n\", \"23\\n\", \"6\\n\", \"-1\\n\", \"5\\n\", \"-1\\n\", \"26\\n\", \"2\\n\", \"18\\n\", \"11\\n\", \"23\\n\", \"6\\n\", \"-1\\n\", \"4\\n\", \"5\\n\", \"-1\\n\", \"13\\n\", \"-1\\n\", \"42\\n\", \"6\\n\", \"-1\\n\", \"4\\n\", \"5\\n\", \"-1\\n\", \"5\", \"28\", \"-1\"]}", "source": "taco"}
|
We have N points numbered 1 to N arranged in a line in this order.
Takahashi decides to make an undirected graph, using these points as the vertices. In the beginning, the graph has no edge. Takahashi will do M operations to add edges in this graph. The i-th operation is as follows:
* The operation uses integers L_i and R_i between 1 and N (inclusive), and a positive integer C_i. For every pair of integers (s, t) such that L_i \leq s < t \leq R_i, add an edge of length C_i between Vertex s and Vertex t.
The integers L_1, ..., L_M, R_1, ..., R_M, C_1, ..., C_M are all given as input.
Takahashi wants to solve the shortest path problem in the final graph obtained. Find the length of the shortest path from Vertex 1 to Vertex N in the final graph.
Constraints
* 2 \leq N \leq 10^5
* 1 \leq M \leq 10^5
* 1 \leq L_i < R_i \leq N
* 1 \leq C_i \leq 10^9
Input
Input is given from Standard Input in the following format:
N M
L_1 R_1 C_1
:
L_M R_M C_M
Output
Print the length of the shortest path from Vertex 1 to Vertex N in the final graph. If there is no shortest path, print `-1` instead.
Examples
Input
4 3
1 3 2
2 4 3
1 4 6
Output
5
Input
4 2
1 2 1
3 4 2
Output
-1
Input
10 7
1 5 18
3 4 8
1 3 5
4 7 10
5 9 8
6 10 5
8 10 3
Output
28
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"10\\nGGGSGGGSGG\\n\", \"4\\nGGGG\\n\", \"3\\nSSS\\n\", \"11\\nSGGGGSGGGGS\\n\", \"300\\nSSGSGSSSGSGSSSSGGSGSSGGSGSGGSSSGSSGSGGSSGGSGSSGGSGGSSGSSSGSGSGSSGSGGSSSGSSGSSGGGGSSGSSGSSGSGGSSSSGGGGSSGSSSSSSSSGSSSSGSGSSSSSSSSGSGSSSSGSSGGSSGSGSSSSSSGSGSSSGGSSGSGSSGSSSSSSGGGSSSGSGSGSGGSGGGSSGSGSSSGSSGGSSGSSGGGGSGSSGSSSSGGSSSSGGSGSSSSSSGSSSGGGSGSGGSSGSSSSSSGGSSSGSSSSGGGSSGSSSGSGGGSSSSGSSSGSGSGGGGS\\n\", \"2\\nSS\\n\", \"2\\nSG\\n\", \"2\\nGS\\n\", \"2\\nGG\\n\", \"6\\nGGSSGG\\n\", \"5\\nGGSSG\\n\", \"11\\nSGGGGGSSSSG\\n\", \"7\\nGGGSSSG\\n\", \"15\\nGGSSGGGGGGGSSGG\\n\", \"6\\nGSSSGG\\n\", \"4\\nGSSG\\n\", \"10\\nGSSGGGGSSG\\n\", \"8\\nGSSSGGGG\\n\", \"8\\nSGGSGGGG\\n\", \"12\\nGGGSSGGGGSSG\\n\", \"4\\nGSGG\\n\", \"7\\nGGGSSGG\\n\", \"10\\nGGGSSGGGGG\\n\", \"12\\nSSSGGSSSGGGG\\n\", \"10\\nGGSSGGSSGG\\n\", \"5\\nGSSSG\\n\", \"10\\nGGGGGGGSSG\\n\", \"6\\nGSSSSG\\n\", \"10\\nGGGGSSSGGG\\n\", \"6\\nGGGSGG\\n\", \"6\\nGSSGSG\\n\", \"9\\nGGGGSSGGG\\n\", \"8\\nSGSSGGGG\\n\", \"5\\nGSSGS\\n\", \"6\\nGGGSSG\\n\", \"94\\nGGSSGGSGGSSSSSGSSSGGSSSSSGSGGGGSGSGSGSGSGSSSSGGGSSGSSSSGSSSSSSSSSGSSSGGSSGGSGSSGSGGGGSGGGSSSSS\\n\", \"20\\nSGSSGGGSSSSSSGGGGGSS\\n\", \"10\\nGSSGSSSSSS\\n\", \"10\\nGSGSGSGSGG\\n\", \"16\\nGSGSSGSSGGGSSSGS\\n\", \"8\\nSGSSGSSG\\n\", \"26\\nGGSSSSGSSSSSSSGSSSSSSGSSGS\\n\", \"10\\nSSGGSSGSSS\\n\", \"20\\nGGGGSSGGGGSGGGSGGGGG\\n\", \"8\\nGGGSSSGG\\n\", \"15\\nGGSGGGSSGGGGGGG\\n\", \"8\\nGSGSSGGG\\n\", \"8\\nGSSGGGGG\\n\", \"10\\nSSSSGGSGGG\\n\", \"21\\nSSSGGGSGGGSSSGGGGGGGG\\n\", \"10\\nGGGGSSGGSG\\n\", \"5\\nGSSGG\\n\", \"7\\nGGSSSSG\\n\", \"7\\nGGGGSSG\\n\", \"17\\nGSGSSGGGSSGGGGSGS\\n\", \"10\\nGGSSGGSSSS\\n\", \"8\\nGSGSGGGG\\n\", \"7\\nGSSGSSG\\n\", \"10\\nGGSSGSSSGG\\n\", \"10\\nSSGGSSGGSS\\n\", \"20\\nGSGGSSGGGSSSGGGGSSSS\\n\", \"7\\nGSGGSGG\\n\", \"9\\nGGGSSGGSG\\n\", \"3\\nSGS\\n\", \"10\\nSSGGGSSGGS\\n\", \"4\\nGSSS\\n\", \"7\\nGGSSGGG\\n\", \"73\\nSGSGGGGSSGSGSGGGSSSSSGGSGGSSSGSGSGSSSSGSGGGSSSSGSSGSGSSSGSGGGSSGGGGGGGSSS\\n\", \"9\\nGGGSSGGGG\\n\", \"10\\nSGSGGSGGGG\\n\", \"5\\nSSGSS\\n\", \"5\\nGGSSS\\n\", \"10\\nGGGGSSGGGG\\n\", \"7\\nSGGSSGG\\n\", \"5\\nSGSSG\\n\", \"3\\nGSG\\n\", \"7\\nGGSSGGS\\n\", \"8\\nSSSGSSGG\\n\", \"3\\nSSG\\n\", \"8\\nGGGSSGGG\\n\", \"11\\nSGSGSGGGSSS\\n\", \"6\\nGGSSSG\\n\", \"6\\nGSGSGG\\n\", \"8\\nSSSGGSGG\\n\", \"10\\nGSSSSGGGGG\\n\", \"7\\nGSSGGSG\\n\", \"10\\nGSSSSSSSGG\\n\", \"5\\nSSGGG\\n\", \"6\\nSSSSSS\\n\", \"7\\nGGSGGSG\\n\", \"20\\nSSSSSGGGGSGGGGGGGGGG\\n\", \"6\\nGSSGGS\\n\", \"8\\nGSSGSSGG\\n\", \"6\\nGSSGGG\\n\", \"5\\nSGSSS\\n\", \"3\\nGGS\\n\", \"10\\nSGGGSSGGSS\\n\", \"3\\nGSS\\n\", \"11\\nGSSSGGGGGGG\\n\", \"10\\nSSSGGSGGGG\\n\", \"6\\nSGGSSG\\n\", \"6\\nSGSSGG\\n\", \"20\\nSSGSSGGGGSGGGGGGGGGG\\n\", \"8\\nSGGGSSSG\\n\", \"9\\nGSGSSGGGS\\n\", \"89\\nSGGSGSGGSSGGSGGSGGGGSSGSSSSSGGGGGGGGGGSSSSGGGGSSSSSGSSSSSGSGSGSGGGSSSGSGGGSSSGSGSGSSGSSGS\\n\", \"9\\nGGGGGSSGG\\n\", \"9\\nSGSSGSSGS\\n\", \"10\\nGGGSSSGGGS\\n\", \"20\\nSGSSSGGGGSGGGGGGGGGG\\n\", \"7\\nGSSGGGG\\n\", \"18\\nGSGSSSSGSSGGGSSSGG\\n\", \"7\\nGSSSSGG\\n\", \"9\\nGSSGGSGGG\\n\", \"17\\nSSSSGSGSGSGSGSGGG\\n\", \"9\\nGGSSGGGGS\\n\", \"8\\nGSSGGSSG\\n\", \"15\\nSGGSSGGSGGSGGGS\\n\", \"7\\nGSSSGSG\\n\", \"10\\nGSSSGSSSSG\\n\", \"8\\nSGGSSGGS\\n\", \"13\\nSSGGSSSSGSSSS\\n\", \"19\\nGSGGGSSSGGGGGGGGGGG\\n\", \"15\\nGSGGSGGSSGGGGGG\\n\", \"6\\nSGSGSS\\n\", \"46\\nGGGGGGGSSSSGGSGGGSSGSSGSSGGGSGSGGSSGSSSSGGSSSS\\n\", \"6\\nGGSGGG\\n\", \"40\\nGSSGGGGGGGSSSGSGSSGGGSSSSGSGSSSSGSSSGSSS\\n\", \"8\\nGGSSSSSG\\n\", \"32\\nGSGSSGGSGGSGGSGGSGGSGSGGSSSGGGGG\\n\", \"8\\nGSGGSGGS\\n\", \"8\\nGGSSSGGG\\n\", \"10\\nSGGSGGSGGG\\n\", \"10\\nSSSGGGSSSG\\n\", \"7\\nSSGGSSG\\n\", \"13\\nGSGSSSSSSGGGG\\n\", \"12\\nGGSGGSSGGGGG\\n\", \"9\\nSGGSGGSGG\\n\", \"30\\nGGGGGGSSGGSSSGSSGSSGSSSGGSSSGG\\n\", \"11\\nGSGSGSSSGGG\\n\", \"10\\nSGGGGGGSSG\\n\", \"9\\nSSSGGSSGS\\n\", \"20\\nSGGGSSGGGGSSGSGGSSGS\\n\", \"5\\nSGGSS\\n\", \"4\\nGGGS\\n\", \"90\\nSSGSGGSGSGGGSSSSSGSGSSSGGSSGSGSGSSGGGSGGSGGGSSSSSGSGGGSSSSSGSSSSGGSGGSSSSGGGSSSGSSSGGGSGGG\\n\", \"30\\nSGGGGSSSGSGSSSSSSGGGGSSGGSSSGS\\n\", \"11\\nGGSGSSGGGGG\\n\", \"10\\nGGGSSGGSGG\\n\", \"10\\nSGSGGGGSGG\\n\", \"4\\nSSSS\\n\", \"9\\nGGSGSSSGG\\n\", \"14\\nGSGSSSSGGGSSGS\\n\", \"3\\nSGG\\n\", \"9\\nGGGSSGGSS\\n\", \"8\\nGSSSGSGG\\n\", \"9\\nSSSSGGSGG\\n\", \"4\\nSSGG\\n\", \"38\\nGSSSSSGGGSSGGGGSSSSSSGGGSSGSSGGGSSGGSS\\n\", \"5\\nGGSGG\\n\", \"4\\nSGGS\\n\", \"10\\nSSGSSSGGGS\\n\", \"5\\nGSGSG\\n\", \"5\\nSSGSG\\n\", \"5\\nGSGGG\\n\", \"11\\nSSGSSGGGSSG\\n\", \"9\\nSSGGGSGSS\\n\", \"4\\nGGSG\\n\", \"8\\nGGSSSGGS\\n\", \"6\\nSGGSGG\\n\", \"10\\nSSGGSSSSSS\\n\", \"10\\nGGGSGGGGSS\\n\", \"170\\nSGSGSGGGGGGSGSSGSGSGGSGGGGGGSSSGSGSGGSGGSGSGGGGSSSSSGSSGSSSSSGSGGGSGGSGSGSSGSSSGGSSGGGSGGGSSGGSGSGGSGGGGSGGGSSSGGGGSSSSSSGGSGSSSGSGGSSGGSGSGSGGGGSSSGGGGGGSGGSGGGGGGSGGGGS\\n\", \"10\\nSGSGSSGGGG\\n\", \"183\\nGSSSSGGSSGSGSSGGGGGSGSSGGGSSSSGGGSSSGSGSSSSGSGGSGSGSGGSGGGSSSGSGSGSSSGSGSGSGGSGSGGGGGSSGSGGGGSGGGGSSGGGSSSGSGGGSGGSSSGSGSSSSSSSSSSGSSGSGSSGGSGSSSGGGSGSGSGSGSSSSGGGSGSGGGGGSGSSSSSGGSSG\\n\", \"123\\nGSSSSGGGSSSGSGGSGGSGGGGGGSGSGGSGSGGGGGGGSSGGSGGGGSGGSGSSSSSSGGGSGGGGGGGSGGGSSGSSSGGGGSGGGSSGSSGSSGSSGGSGGSGSSSSGSSGGGGGGSSS\\n\", \"100\\nSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS\\n\", \"174\\nGGGGSSSGGGGSGGSSSGSSSGGGGGGGSSSSSSSSGGSGSSSSGGGSSGSGGSGSSSSSGGGSSGGGGSGSSGSSGSGSSSGGSGSGSGSSSGSGGSGGSSGGSSSSGSSGSSGGSSGSSGGGGSSGSSGGGGGSSSSGGGGSSGSGSGSGGGSGSGGGSGGGSGSGSGGGGG\\n\", \"181\\nGGGGGGGGGGGSSGGGGGGGSSSGSSSSGSSGSSSGGSGGSGGSSGSSGSSGGSGGGSSGGGSGGGGGSGGGSGSGSGSSGSSGGSGGGGSSGGSGGSGSSSSGSSGGSGGSSSGSSGSSGGGSGSSGGGSGSSGGGSSSSSSGGSSSSGSGSSSSSGGSGSSSGGGGSSGGGSGGGSGSS\\n\", \"169\\nGSGSGSGGSGSSSGSSGSGGGSGGGSSSGGSGSSSSSGGGGSSSSGGGSSGSGGSGGSGGSSGGGGSSGSSGSSSGSGGSSGGSSGGSSGSGSSGSSSSSSGSGSSGSSSGGSGSGGSSSSGSGGSGSSSSGSGGSSGGGSGGSGGSSSSGSSGSSSSSGGGGGGGSGS\\n\", \"33\\nGGGGSSSGGSSSGGGGGGGSGGGGSGGGGGGGG\\n\", \"134\\nGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGS\\n\", \"11\\nSSGSSGGGSSG\\n\", \"10\\nSGGGSSGGSS\\n\", \"10\\nGSGSGSGSGG\\n\", \"6\\nGSSGGG\\n\", \"32\\nGSGSSGGSGGSGGSGGSGGSGSGGSSSGGGGG\\n\", \"11\\nGSSSGGGGGGG\\n\", \"4\\nGGGS\\n\", \"100\\nSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS\\n\", \"11\\nSGGGGGSSSSG\\n\", \"11\\nGSGSGSSSGGG\\n\", \"12\\nGGSGGSSGGGGG\\n\", \"5\\nGGSSS\\n\", \"8\\nSGSSGSSG\\n\", \"9\\nSGGSGGSGG\\n\", \"3\\nSGS\\n\", \"9\\nGGGSSGGSG\\n\", \"8\\nSGSSGGGG\\n\", \"94\\nGGSSGGSGGSSSSSGSSSGGSSSSSGSGGGGSGSGSGSGSGSSSSGGGSSGSSSSGSSSSSSSSSGSSSGGSSGGSGSSGSGGGGSGGGSSSSS\\n\", \"10\\nSSGGSSGGSS\\n\", \"10\\nGSSSGSSSSG\\n\", \"13\\nGSGSSSSSSGGGG\\n\", \"6\\nGSGSGG\\n\", \"15\\nGGSGGGSSGGGGGGG\\n\", \"8\\nGSSGGGGG\\n\", \"6\\nGSSGSG\\n\", \"5\\nSGGSS\\n\", \"2\\nSG\\n\", \"123\\nGSSSSGGGSSSGSGGSGGSGGGGGGSGSGGSGSGGGGGGGSSGGSGGGGSGGSGSSSSSSGGGSGGGGGGGSGGGSSGSSSGGGGSGGGSSGSSGSSGSSGGSGGSGSSSSGSSGGGGGGSSS\\n\", \"5\\nGSSGS\\n\", \"8\\nGSSSGSGG\\n\", \"8\\nGGSSSGGS\\n\", \"8\\nGSSGSSGG\\n\", \"10\\nSSSSGGSGGG\\n\", \"38\\nGSSSSSGGGSSGGGGSSSSSSGGGSSGSSGGGSSGGSS\\n\", \"8\\nGGGSSGGG\\n\", \"5\\nSSGSS\\n\", \"7\\nGSSGGGG\\n\", \"11\\nSGSGSGGGSSS\\n\", \"6\\nGGSSSG\\n\", \"6\\nSGSSGG\\n\", \"5\\nGSGSG\\n\", \"20\\nGGGGSSGGGGSGGGSGGGGG\\n\", \"7\\nGGSSSSG\\n\", \"10\\nSGGSGGSGGG\\n\", \"5\\nSGSSG\\n\", \"3\\nSSG\\n\", \"7\\nGGSSGGS\\n\", \"20\\nSSSSSGGGGSGGGGGGGGGG\\n\", \"7\\nGGGSSSG\\n\", \"6\\nSGSGSS\\n\", \"33\\nGGGGSSSGGSSSGGGGGGGSGGGGSGGGGGGGG\\n\", \"2\\nGG\\n\", \"8\\nSSSGGSGG\\n\", \"5\\nGGSSG\\n\", \"30\\nSGGGGSSSGSGSSSSSSGGGGSSGGSSSGS\\n\", \"6\\nGSSSSG\\n\", \"10\\nSGSGGSGGGG\\n\", \"6\\nSSSSSS\\n\", \"90\\nSSGSGGSGSGGGSSSSSGSGSSSGGSSGSGSGSSGGGSGGSGGGSSSSSGSGGGSSSSSGSSSSGGSGGSSSSGGGSSSGSSSGGGSGGG\\n\", \"20\\nSGSSSGGGGSGGGGGGGGGG\\n\", \"30\\nGGGGGGSSGGSSSGSSGSSGSSSGGSSSGG\\n\", \"300\\nSSGSGSSSGSGSSSSGGSGSSGGSGSGGSSSGSSGSGGSSGGSGSSGGSGGSSGSSSGSGSGSSGSGGSSSGSSGSSGGGGSSGSSGSSGSGGSSSSGGGGSSGSSSSSSSSGSSSSGSGSSSSSSSSGSGSSSSGSSGGSSGSGSSSSSSGSGSSSGGSSGSGSSGSSSSSSGGGSSSGSGSGSGGSGGGSSGSGSSSGSSGGSSGSSGGGGSGSSGSSSSGGSSSSGGSGSSSSSSGSSSGGGSGSGGSSGSSSSSSGGSSSGSSSSGGGSSGSSSGSGGGSSSSGSSSGSGSGGGGS\\n\", \"9\\nGGGGGSSGG\\n\", \"4\\nSSSS\\n\", \"10\\nSGSGSSGGGG\\n\", \"8\\nGGSSSGGG\\n\", \"9\\nGGSGSSSGG\\n\", \"6\\nGGSSGG\\n\", \"8\\nGSGGSGGS\\n\", \"10\\nSSSGGGSSSG\\n\", \"4\\nGGSG\\n\", \"10\\nSSGGSSGSSS\\n\", \"20\\nSSGSSGGGGSGGGGGGGGGG\\n\", \"6\\nSGGSSG\\n\", \"12\\nGGGSSGGGGSSG\\n\", \"8\\nGSGSGGGG\\n\", \"7\\nGSGGSGG\\n\", \"17\\nGSGSSGGGSSGGGGSGS\\n\", \"26\\nGGSSSSGSSSSSSSGSSSSSSGSSGS\\n\", \"9\\nGSGSSGGGS\\n\", \"10\\nGGSSGGSSSS\\n\", \"5\\nSGSSS\\n\", \"8\\nSGGGSSSG\\n\", \"3\\nGSS\\n\", \"15\\nGGSSGGGGGGGSSGG\\n\", \"9\\nSSSSGGSGG\\n\", \"5\\nSSGGG\\n\", \"10\\nSSGSSSGGGS\\n\", \"20\\nSGGGSSGGGGSSGSGGSSGS\\n\", \"12\\nSSSGGSSSGGGG\\n\", \"9\\nSSSGGSSGS\\n\", \"10\\nGGGGSSGGSG\\n\", \"7\\nGGSGGSG\\n\", \"4\\nSGGS\\n\", \"10\\nSSGGGSSGGS\\n\", \"21\\nSSSGGGSGGGSSSGGGGGGGG\\n\", \"2\\nGS\\n\", \"89\\nSGGSGSGGSSGGSGGSGGGGSSGSSSSSGGGGGGGGGGSSSSGGGGSSSSSGSSSSSGSGSGSGGGSSSGSGGGSSSGSGSGSSGSSGS\\n\", \"8\\nSGGSSGGS\\n\", \"8\\nGGGSSSGG\\n\", \"7\\nGGGSSGG\\n\", \"8\\nSGGSGGGG\\n\", \"4\\nGSSS\\n\", \"6\\nGGGSGG\\n\", \"73\\nSGSGGGGSSGSGSGGGSSSSSGGSGGSSSGSGSGSSSSGSGGGSSSSGSSGSGSSSGSGGGSSGGGGGGGSSS\\n\", \"10\\nGSSGSSSSSS\\n\", \"6\\nSGGSGG\\n\", \"15\\nSGGSSGGSGGSGGGS\\n\", \"7\\nGSSSSGG\\n\", \"7\\nSGGSSGG\\n\", \"20\\nSGSSGGGSSSSSSGGGGGSS\\n\", \"7\\nGSSGSSG\\n\", \"10\\nGSSSSGGGGG\\n\", \"9\\nSSGGGSGSS\\n\", \"3\\nGGS\\n\", \"8\\nGSSGGSSG\\n\", \"183\\nGSSSSGGSSGSGSSGGGGGSGSSGGGSSSSGGGSSSGSGSSSSGSGGSGSGSGGSGGGSSSGSGSGSSSGSGSGSGGSGSGGGGGSSGSGGGGSGGGGSSGGGSSSGSGGGSGGSSSGSGSSSSSSSSSSGSSGSGSSGGSGSSSGGGSGSGSGSGSSSSGGGSGSGGGGGSGSSSSSGGSSG\\n\", \"10\\nSGSGGGGSGG\\n\", \"14\\nGSGSSSSGGGSSGS\\n\", \"5\\nGGSGG\\n\", \"5\\nGSGGG\\n\", \"8\\nGSGSSGGG\\n\", \"5\\nSSGSG\\n\", \"15\\nGSGGSGGSSGGGGGG\\n\", \"10\\nGGSSGGSSGG\\n\", \"19\\nGSGGGSSSGGGGGGGGGGG\\n\", \"8\\nGGSSSSSG\\n\", \"8\\nGSSSGGGG\\n\", \"20\\nGSGGSSGGGSSSGGGGSSSS\\n\", \"9\\nSGSSGSSGS\\n\", \"3\\nSGG\\n\", \"13\\nSSGGSSSSGSSSS\\n\", \"5\\nGSSSG\\n\", \"10\\nGSSSSSSSGG\\n\", \"40\\nGSSGGGGGGGSSSGSGSSGGGSSSSGSGSSSSGSSSGSSS\\n\", \"10\\nGGGGGGGSSG\\n\", \"181\\nGGGGGGGGGGGSSGGGGGGGSSSGSSSSGSSGSSSGGSGGSGGSSGSSGSSGGSGGGSSGGGSGGGGGSGGGSGSGSGSSGSSGGSGGGGSSGGSGGSGSSSSGSSGGSGGSSSGSSGSSGGGSGSSGGGSGSSGGGSSSSSSGGSSSSGSGSSSSSGGSGSSSGGGGSSGGGSGGGSGSS\\n\", \"11\\nSGGGGSGGGGS\\n\", \"6\\nGGGSSG\\n\", \"4\\nGSGG\\n\", \"169\\nGSGSGSGGSGSSSGSSGSGGGSGGGSSSGGSGSSSSSGGGGSSSSGGGSSGSGGSGGSGGSSGGGGSSGSSGSSSGSGGSSGGSSGGSSGSGSSGSSSSSSGSGSSGSSSGGSGSGGSSSSGSGGSGSSSSGSGGSSGGGSGGSGGSSSSGSSGSSSSSGGGGGGGSGS\\n\", \"2\\nSS\\n\", \"10\\nGGSSGSSSGG\\n\", \"174\\nGGGGSSSGGGGSGGSSSGSSSGGGGGGGSSSSSSSSGGSGSSSSGGGSSGSGGSGSSSSSGGGSSGGGGSGSSGSSGSGSSSGGSGSGSGSSSGSGGSGGSSGGSSSSGSSGSSGGSSGSSGGGGSSGSSGGGGGSSSSGGGGSSGSGSGSGGGSGSGGGSGGGSGSGSGGGGG\\n\", \"10\\nGGGGSSGGGG\\n\", \"9\\nGGGSSGGGG\\n\", \"10\\nGGGSSSGGGS\\n\", \"4\\nSSGG\\n\", \"9\\nGSSGGSGGG\\n\", \"7\\nGSSSGSG\\n\", \"10\\nSSSGGSGGGG\\n\", \"7\\nGGGGSSG\\n\", \"46\\nGGGGGGGSSSSGGSGGGSSGSSGSSGGGSGSGGSSGSSSSGGSSSS\\n\", \"16\\nGSGSSGSSGGGSSSGS\\n\", \"7\\nSSGGSSG\\n\", \"10\\nGGGSGGGGSS\\n\", \"10\\nGGGSSGGSGG\\n\", \"10\\nSGGGGGGSSG\\n\", \"10\\nGSSGGGGSSG\\n\", \"7\\nGSSGGSG\\n\", \"4\\nGSSG\\n\", \"11\\nGGSGSSGGGGG\\n\", \"6\\nGGSGGG\\n\", \"17\\nSSSSGSGSGSGSGSGGG\\n\", \"9\\nGGSSGGGGS\\n\", \"10\\nGGGGSSSGGG\\n\", \"7\\nGGSSGGG\\n\", \"10\\nGGGSSGGGGG\\n\", \"9\\nGGGSSGGSS\\n\", \"3\\nGSG\\n\", \"10\\nSSGGSSSSSS\\n\", \"6\\nGSSSGG\\n\", \"170\\nSGSGSGGGGGGSGSSGSGSGGSGGGGGGSSSGSGSGGSGGSGSGGGGSSSSSGSSGSSSSSGSGGGSGGSGSGSSGSSSGGSSGGGSGGGSSGGSGSGGSGGGGSGGGSSSGGGGSSSSSSGGSGSSSGSGGSSGGSGSGSGGGGSSSGGGGGGSGGSGGGGGGSGGGGS\\n\", \"9\\nGGGGSSGGG\\n\", \"5\\nGSSGG\\n\", \"18\\nGSGSSSSGSSGGGSSSGG\\n\", \"6\\nGSSGGS\\n\", \"8\\nSSSGSSGG\\n\", \"134\\nGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGS\\n\", \"11\\nGSSSSGGGSSG\\n\", \"9\\nGGSGGSGGS\\n\", \"94\\nSSSSSGGGSGGGGSGSSGSGGSSGGSSSGSSSSSSSSSGSSSSGSSGGGSSSSGSGSGSGSGSGGGGSGSSSSSGGSSSGSSSSSGGSGGSSGG\\n\", \"6\\nGSGSSG\\n\", \"123\\nSSSGGGGGGSSGSSSSGSGGSGGSSGSSGSSGSSGGGSGGGGSSSGSSGGGSGGGGGGGSGGGSSSSSSGSGGSGGGGSGGSSGGGGGGGSGSGGSGSGGGGGGSGGSGGSGSSSGGGSSSSG\\n\", \"6\\nSSSGSG\\n\", \"33\\nGGGSSSSGGSSSGGGGGGGGGGGGSGGGGGGGG\\n\", \"10\\nGGGGSGGSGS\\n\", \"9\\nGGSGGGSGG\\n\", \"20\\nGGGGGGGGGGSGGGGSSGSS\\n\", \"5\\nSSSGS\\n\", \"21\\nGGGGGGGGSSSGGGSGGGSSS\\n\", \"89\\nSGGSGSGGSSGGSGGSGGSGSSGSSSSSGGGGGGGGGGGSSSGGGGSSSSSGSSSSSGSGSGSGGGSSSGSGGGSSSGSGSGSSGSSGS\\n\", \"20\\nGSGGSSGGGGGGGGSGGGGG\\n\", \"10\\nSSGGSSGGGS\\n\", \"9\\nGSGGSSGGG\\n\", \"8\\nGGGGSSGS\\n\", \"10\\nSSGSSGGGSS\\n\", \"13\\nGGGGSSSSSSGSG\\n\", \"8\\nSGGSSSGG\\n\", \"10\\nGGGSGGSSSS\\n\", \"38\\nSSGGSSGGGSSGSSGGGSSSSSSGGGGSSGGGSSSSSG\\n\", \"7\\nGGSGSGG\\n\", \"7\\nGGSSSGG\\n\", \"8\\nGGSGGSSS\\n\", \"30\\nGGSSSGGSSSGSSGSSGSSSGGSSGGGGGG\\n\", \"9\\nGGSSSGSGG\\n\", \"6\\nGGSGSG\\n\", \"4\\nSGGG\\n\", \"10\\nSSSGSSGGSS\\n\", \"12\\nGSGSSGGGGSGG\\n\", \"8\\nGGGGSGSG\\n\", \"7\\nSSGGGGG\\n\", \"26\\nGSSGSSGSSSSSSSGSSSSSSGSSGS\\n\", \"8\\nSGSGSGSG\\n\", \"15\\nGGGSGGSGGGGSSGG\\n\", \"9\\nGGSGGSSSS\\n\", \"5\\nGGGSS\\n\", \"10\\nSGGGSSSGSS\\n\", \"12\\nGGGGSSSGGSSS\\n\", \"9\\nSSSGGSGSS\\n\", \"10\\nGGGSSSGGGG\\n\", \"4\\nGGSS\\n\", \"8\\nSSGGSGGS\\n\", \"8\\nGGGGSGGS\\n\", \"6\\nGGSGGS\\n\", \"20\\nSGSSGGSSSSSSGGGGGGSS\\n\", \"183\\nGSSGGSSSSSGSGGGGGSGSGGGSSSSGSGSGSGSGGGSSSGSGGSSGSGSSGSSSSSSSSSSGSGSSSGGSGGGSGSSSGGGSSGGGGSGGGGSGSSGGGGGSGSGGSGSGSGSSSGSGSGSSSGGGSGGSGSGSGGSGSSSSGSGSSSGGGSSSSGGGSSGSGGGGGSSGSGSSGGSSSSG\\n\", \"8\\nGGGSSGSG\\n\", \"10\\nGGSSSSSSSG\\n\", \"181\\nSSGSGGGSGGGSSGGGGSSSGSGGSSSSSGSGSSSSGGSSSSSSGGGSSGSGGGSSGSGGGSSGSSGSSSGGSGGSSGSSSSGSGGSGGSSGGGGSGGSSGSSGSGSGSGGGSGGGGGSGGGSSGGGSGGSSGSSGSSGGSGGSGGSSSGSSGSSSSGSSSGGGGGGGSSGGGGGGGGGGG\\n\", \"169\\nSGSGGGGGGGSSSSSGSSGSSSSGGSGGSGGGSSGGSGSSSSGSGGSGSSSSGGSGSGGSSSGSSGSGSSSSSSGSSGSGSSGGSSGGSSGGSGSSSGSSGSSGGGGSSGGSGGSGGSGSSGGGSSSSGGGGSSSSSGSGGSSSGGGSGGGSGSSGSSSGSGGSGSGSG\\n\", \"10\\nGGSSSGSSGG\\n\", \"174\\nGGGGGSGSGSGGGSGGGSGSGGGSGSGSGSSGGGGSSSSGGGGGSSGSSGGGGSSGSSGGSSGSSGSSSSGGSSGGSGGSGSSSGSGSGSGGSSSGSGSSGSSGSGGGGSSGGGSSSSSGSGGSGSSGGGSSSSGSGGSSSSSSSSGGGGGGGSSSGSSSGGSGGGGSSSGGGG\\n\", \"10\\nGGGGSGGSSS\\n\", \"10\\nGGGGGGSGSS\\n\", \"10\\nSGSGGGGSSG\\n\", \"11\\nGGGGGSSGSGG\\n\", \"17\\nGGGSGSGSGSGSGSSSS\\n\", \"10\\nGGGGGSSSGG\\n\", \"134\\nSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSGSG\\n\", \"11\\nGSSGGGSSSSG\\n\", \"9\\nGGGGGSGSS\\n\", \"10\\nGSGGGGSSSS\\n\", \"33\\nGGGGGGGGSGGGGGGGGGGGGSSSGGSSSSGGG\\n\", \"12\\nGGSGGGGSSGSG\\n\", \"26\\nSGSSGSSSSSSGSSSSSSSGSSGSSG\\n\", \"9\\nGSSGGSGSS\\n\", \"10\\nSGSGSGSGSS\\n\", \"8\\nSGGSGGSS\\n\", \"10\\nSSGSGGGGGG\\n\", \"11\\nSGGGGSGGSGG\\n\", \"9\\nSSGSGGGGG\\n\", \"12\\nGGSSGGGSSGGG\\n\", \"9\\nGSSSGGGSS\\n\", \"8\\nSGSSGGGS\\n\", \"12\\nGGGSSGGGSSGG\\n\", \"9\\nGSGSSGGSS\\n\", \"8\\nSGGSGSGS\\n\", \"9\\nSSGGSSGSG\\n\", \"8\\nSGSGSGGS\\n\", \"32\\nGGGGGSSSGGSGSGGSGGSGGSGGSGGSSGSG\\n\", \"11\\nGGGGGGGSSSG\\n\", \"11\\nGSSSSGGGGGS\\n\", \"9\\nSGSGGGSGG\\n\", \"15\\nGGGGGGGSSGGGSGG\\n\", \"8\\nGSGGGGGS\\n\", \"5\\nSSGGS\\n\", \"5\\nSSSGG\\n\", \"8\\nGGSSSGSG\\n\", \"38\\nSSSSSSGGGSSGGGGSSGSSSGGGSSGSSGGGSSGGSS\\n\", \"8\\nSGGGSGGG\\n\", \"7\\nGSGSGGG\\n\", \"11\\nSGSGGGGSSSS\\n\", \"6\\nGGSGSS\\n\", \"6\\nSGSGSG\\n\", \"4\\nGGGG\\n\", \"10\\nGGGSGGGSGG\\n\", \"3\\nSSS\\n\"], \"outputs\": [\"7\\n\", \"4\\n\", \"0\\n\", \"8\\n\", \"6\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"3\\n\", \"3\\n\", \"6\\n\", \"4\\n\", \"8\\n\", \"3\\n\", \"2\\n\", \"5\\n\", \"5\\n\", \"6\\n\", \"5\\n\", \"3\\n\", \"4\\n\", \"6\\n\", \"5\\n\", \"3\\n\", \"2\\n\", \"8\\n\", \"2\\n\", \"5\\n\", \"5\\n\", \"3\\n\", \"5\\n\", \"5\\n\", \"2\\n\", \"4\\n\", \"8\\n\", \"6\\n\", \"2\\n\", \"4\\n\", \"4\\n\", \"2\\n\", \"3\\n\", \"3\\n\", \"9\\n\", \"4\\n\", \"8\\n\", \"4\\n\", \"6\\n\", \"5\\n\", \"9\\n\", \"5\\n\", \"3\\n\", \"3\\n\", \"5\\n\", \"6\\n\", \"3\\n\", \"6\\n\", \"2\\n\", \"3\\n\", \"3\\n\", \"5\\n\", \"5\\n\", \"4\\n\", \"1\\n\", \"4\\n\", \"1\\n\", \"4\\n\", \"8\\n\", \"5\\n\", \"7\\n\", \"1\\n\", \"2\\n\", \"5\\n\", \"3\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"3\\n\", \"1\\n\", \"4\\n\", \"5\\n\", \"3\\n\", \"4\\n\", \"4\\n\", \"6\\n\", \"4\\n\", \"3\\n\", \"3\\n\", \"0\\n\", \"5\\n\", \"14\\n\", \"3\\n\", \"3\\n\", \"4\\n\", \"1\\n\", \"2\\n\", \"4\\n\", \"1\\n\", \"8\\n\", \"6\\n\", \"3\\n\", \"3\\n\", \"15\\n\", \"4\\n\", \"4\\n\", \"11\\n\", \"6\\n\", \"2\\n\", \"4\\n\", \"15\\n\", \"5\\n\", \"4\\n\", \"3\\n\", \"6\\n\", \"5\\n\", \"5\\n\", \"3\\n\", \"6\\n\", \"3\\n\", \"2\\n\", \"3\\n\", \"3\\n\", \"12\\n\", \"7\\n\", \"2\\n\", \"8\\n\", \"5\\n\", \"8\\n\", \"3\\n\", \"6\\n\", \"5\\n\", \"4\\n\", \"6\\n\", \"4\\n\", \"3\\n\", \"5\\n\", \"6\\n\", \"5\\n\", \"7\\n\", \"4\\n\", \"7\\n\", \"3\\n\", \"5\\n\", \"2\\n\", \"3\\n\", \"7\\n\", \"5\\n\", \"6\\n\", \"5\\n\", \"7\\n\", \"0\\n\", \"4\\n\", \"4\\n\", \"2\\n\", \"4\\n\", \"4\\n\", \"4\\n\", \"2\\n\", \"5\\n\", \"4\\n\", \"2\\n\", \"4\\n\", \"3\\n\", \"2\\n\", \"4\\n\", \"4\\n\", \"4\\n\", \"3\\n\", \"3\\n\", \"4\\n\", \"2\\n\", \"7\\n\", \"11\\n\", \"5\\n\", \"9\\n\", \"11\\n\", \"0\\n\", \"8\\n\", \"12\\n\", \"9\\n\", \"13\\n\", \"3\\n\", \"4\\n\", \"4\\n\", \"4\\n\", \"4\\n\", \"6\\n\", \"8\\n\", \"3\\n\", \"0\", \"6\\n\", \"4\\n\", \"6\\n\", \"2\\n\", \"2\\n\", \"5\\n\", \"1\\n\", \"4\\n\", \"5\\n\", \"8\\n\", \"3\\n\", \"2\\n\", \"5\\n\", \"4\\n\", \"8\\n\", \"6\\n\", \"3\\n\", \"2\\n\", \"1\\n\", \"11\\n\", \"2\\n\", \"4\\n\", \"3\\n\", \"3\\n\", \"5\\n\", \"5\\n\", \"4\\n\", \"1\\n\", \"5\\n\", \"5\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"9\\n\", \"3\\n\", \"6\\n\", \"2\\n\", \"1\\n\", \"3\\n\", \"14\\n\", \"4\\n\", \"2\\n\", \"13\\n\", \"2\", \"4\\n\", \"3\\n\", \"5\\n\", \"2\\n\", \"7\\n\", \"0\", \"7\\n\", \"15\\n\", \"7\\n\", \"6\\n\", \"6\\n\", \"0\", \"5\\n\", \"4\\n\", \"4\\n\", \"3\\n\", \"5\\n\", \"4\\n\", \"3\\n\", \"3\\n\", \"15\\n\", \"3\\n\", \"5\\n\", \"6\\n\", \"5\\n\", \"6\\n\", \"3\\n\", \"4\\n\", \"3\\n\", \"1\\n\", \"4\\n\", \"1\\n\", \"8\\n\", \"4\\n\", \"3\\n\", \"4\\n\", \"5\\n\", \"5\\n\", \"3\\n\", \"5\\n\", \"5\\n\", \"2\\n\", \"4\\n\", \"9\\n\", \"1\\n\", \"11\\n\", \"3\\n\", \"4\\n\", \"4\\n\", \"6\\n\", \"1\\n\", \"5\\n\", \"8\\n\", \"2\\n\", \"4\\n\", \"6\\n\", \"3\\n\", \"3\\n\", \"6\\n\", \"2\\n\", \"6\\n\", \"4\\n\", \"2\\n\", \"3\\n\", \"9\\n\", \"7\\n\", \"4\\n\", \"4\\n\", \"4\\n\", \"4\\n\", \"2\\n\", \"7\\n\", \"3\\n\", \"12\\n\", \"3\\n\", \"5\\n\", \"5\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"2\\n\", \"3\\n\", \"8\\n\", \"8\\n\", \"12\\n\", \"8\\n\", \"4\\n\", \"3\\n\", \"9\\n\", \"0\", \"3\\n\", \"8\\n\", \"5\\n\", \"5\\n\", \"4\\n\", \"2\\n\", \"6\\n\", \"3\\n\", \"6\\n\", \"5\\n\", \"8\\n\", \"4\\n\", \"3\\n\", \"7\\n\", \"5\\n\", \"7\\n\", \"5\\n\", \"4\\n\", \"2\\n\", \"6\\n\", \"5\\n\", \"5\\n\", \"5\\n\", \"5\\n\", \"4\\n\", \"6\\n\", \"4\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"11\\n\", \"5\\n\", \"3\\n\", \"4\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"4\\n\", \"5\\n\", \"8\\n\", \"3\\n\", \"11\\n\", \"2\\n\", \"21\\n\", \"7\\n\", \"6\\n\", \"15\\n\", \"1\\n\", \"9\\n\", \"12\\n\", \"14\\n\", \"4\\n\", \"4\\n\", \"5\\n\", \"4\\n\", \"5\\n\", \"3\\n\", \"5\\n\", \"5\\n\", \"4\\n\", \"3\\n\", \"4\\n\", \"7\\n\", \"4\\n\", \"4\\n\", \"3\\n\", \"3\\n\", \"7\\n\", \"6\\n\", \"5\\n\", \"2\\n\", \"3\\n\", \"7\\n\", \"4\\n\", \"3\\n\", \"4\\n\", \"5\\n\", \"3\\n\", \"5\\n\", \"2\\n\", \"4\\n\", \"6\\n\", \"4\\n\", \"7\\n\", \"9\\n\", \"4\\n\", \"3\\n\", \"12\\n\", \"9\\n\", \"3\\n\", \"8\\n\", \"6\\n\", \"7\\n\", \"6\\n\", \"6\\n\", \"5\\n\", \"6\\n\", \"3\\n\", \"4\\n\", \"6\\n\", \"5\\n\", \"21\\n\", \"7\\n\", \"2\\n\", \"4\\n\", \"3\\n\", \"4\\n\", \"7\\n\", \"7\\n\", \"6\\n\", \"4\\n\", \"4\\n\", \"4\\n\", \"4\\n\", \"3\\n\", \"4\\n\", \"3\\n\", \"4\\n\", \"6\\n\", \"8\\n\", \"6\\n\", \"6\\n\", \"8\\n\", \"6\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"5\\n\", \"6\\n\", \"5\\n\", \"5\\n\", \"3\\n\", \"3\\n\", \"4\", \"7\\n\", \"0\"]}", "source": "taco"}
|
Vova has won $n$ trophies in different competitions. Each trophy is either golden or silver. The trophies are arranged in a row.
The beauty of the arrangement is the length of the longest subsegment consisting of golden trophies. Vova wants to swap two trophies (not necessarily adjacent ones) to make the arrangement as beautiful as possible — that means, to maximize the length of the longest such subsegment.
Help Vova! Tell him the maximum possible beauty of the arrangement if he is allowed to do at most one swap.
-----Input-----
The first line contains one integer $n$ ($2 \le n \le 10^5$) — the number of trophies.
The second line contains $n$ characters, each of them is either G or S. If the $i$-th character is G, then the $i$-th trophy is a golden one, otherwise it's a silver trophy.
-----Output-----
Print the maximum possible length of a subsegment of golden trophies, if Vova is allowed to do at most one swap.
-----Examples-----
Input
10
GGGSGGGSGG
Output
7
Input
4
GGGG
Output
4
Input
3
SSS
Output
0
-----Note-----
In the first example Vova has to swap trophies with indices $4$ and $10$. Thus he will obtain the sequence "GGGGGGGSGS", the length of the longest subsegment of golden trophies is $7$.
In the second example Vova can make no swaps at all. The length of the longest subsegment of golden trophies in the sequence is $4$.
In the third example Vova cannot do anything to make the length of the longest subsegment of golden trophies in the sequence greater than $0$.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"10\\n1 1\\n8 10\\n1 7\\n6 8\\n5 7\\n1 9\\n8 8\\n6 10\\n1 4\\n3 4\\n\", \"10\\n1 4\\n1 12\\n5 7\\n5 5\\n2 5\\n1 7\\n1 10\\n7 9\\n8 9\\n9 11\\n\", \"10\\n6 7\\n5 11\\n5 10\\n9 10\\n11 12\\n6 12\\n7 11\\n1 1\\n5 9\\n2 8\\n\", \"10\\n6 9\\n1 8\\n6 12\\n8 15\\n2 5\\n1 2\\n7 15\\n12 15\\n5 12\\n8 15\\n\", \"10\\n2 4\\n10 13\\n1 10\\n6 13\\n9 12\\n1 10\\n13 15\\n1 11\\n1 7\\n5 6\\n\", \"10\\n10 10\\n13 15\\n6 14\\n3 15\\n4 15\\n11 12\\n11 15\\n8 15\\n1 11\\n1 9\\n\", \"10\\n1 2\\n1 3\\n1 9\\n10 10\\n4 4\\n5 9\\n2 5\\n7 8\\n2 10\\n7 10\\n\", \"10\\n2 8\\n8 10\\n1 6\\n1 10\\n7 10\\n1 9\\n6 8\\n3 4\\n1 3\\n5 8\\n\", \"10\\n1 6\\n4 10\\n1 5\\n5 10\\n1 8\\n4 5\\n1 8\\n4 8\\n5 10\\n10 10\\n\", \"10\\n1 2\\n10 12\\n5 12\\n1 7\\n1 6\\n11 12\\n3 8\\n7 9\\n11 12\\n5 6\\n\", \"10\\n12 12\\n6 13\\n5 9\\n7 11\\n1 12\\n11 15\\n3 13\\n1 14\\n6 8\\n10 10\\n\", \"10\\n1 10\\n3 4\\n8 10\\n3 4\\n5 9\\n1 4\\n7 10\\n1 9\\n1 8\\n4 10\\n\", \"10\\n15 15\\n6 6\\n1 6\\n7 15\\n3 13\\n10 15\\n6 13\\n1 9\\n2 14\\n12 13\\n\", \"10\\n4 12\\n2 8\\n1 12\\n6 8\\n4 6\\n12 12\\n3 10\\n1 10\\n3 3\\n1 10\\n\", \"10\\n3 11\\n2 12\\n7 12\\n5 5\\n6 6\\n1 11\\n11 11\\n1 12\\n1 10\\n7 11\\n\", \"10\\n6 7\\n5 11\\n5 10\\n9 10\\n11 12\\n6 12\\n7 11\\n1 1\\n5 9\\n2 3\\n\", \"10\\n6 9\\n1 8\\n6 12\\n8 15\\n2 5\\n1 2\\n2 15\\n12 15\\n5 12\\n8 15\\n\", \"10\\n2 4\\n10 23\\n1 10\\n6 13\\n9 12\\n1 10\\n13 15\\n1 11\\n1 7\\n5 6\\n\", \"10\\n10 10\\n13 15\\n6 14\\n6 15\\n4 15\\n11 12\\n11 15\\n8 15\\n1 11\\n1 9\\n\", \"10\\n1 2\\n1 3\\n1 18\\n10 10\\n4 4\\n5 9\\n2 5\\n7 8\\n2 10\\n7 10\\n\", \"10\\n1 2\\n10 23\\n5 12\\n1 7\\n1 6\\n11 12\\n3 8\\n7 9\\n11 12\\n5 6\\n\", \"10\\n12 12\\n6 13\\n5 9\\n6 11\\n1 12\\n11 15\\n3 13\\n1 14\\n6 8\\n10 10\\n\", \"10\\n1 10\\n3 4\\n1 10\\n3 4\\n5 9\\n1 4\\n7 10\\n1 9\\n1 8\\n4 10\\n\", \"10\\n15 15\\n6 6\\n1 6\\n7 15\\n3 13\\n10 15\\n6 13\\n2 9\\n2 14\\n12 13\\n\", \"10\\n3 11\\n2 12\\n7 12\\n5 5\\n6 6\\n1 11\\n11 11\\n1 12\\n1 10\\n2 11\\n\", \"10\\n2 4\\n10 23\\n1 10\\n6 13\\n9 12\\n1 10\\n13 15\\n1 11\\n1 10\\n5 6\\n\", \"10\\n10 10\\n13 15\\n6 14\\n10 15\\n4 15\\n11 12\\n11 15\\n8 15\\n1 11\\n1 9\\n\", \"10\\n1 2\\n1 3\\n1 18\\n10 10\\n4 4\\n5 9\\n2 5\\n7 13\\n2 10\\n7 10\\n\", \"10\\n3 11\\n2 12\\n7 12\\n5 5\\n6 6\\n1 21\\n11 11\\n1 12\\n1 10\\n2 11\\n\", \"10\\n15 15\\n6 6\\n1 6\\n7 15\\n3 13\\n10 15\\n6 13\\n2 17\\n2 14\\n12 26\\n\", \"10\\n3 11\\n2 12\\n7 12\\n5 5\\n1 6\\n1 21\\n11 11\\n1 12\\n1 10\\n2 11\\n\", \"10\\n2 4\\n10 10\\n1 10\\n6 22\\n9 12\\n1 10\\n11 15\\n1 11\\n1 10\\n5 6\\n\", \"10\\n3 11\\n2 12\\n5 12\\n5 5\\n1 6\\n1 21\\n11 11\\n1 20\\n2 10\\n2 11\\n\", \"10\\n3 11\\n2 21\\n5 12\\n5 5\\n1 6\\n1 21\\n11 11\\n1 20\\n2 10\\n2 11\\n\", \"10\\n3 11\\n2 21\\n5 12\\n5 5\\n1 6\\n1 21\\n11 11\\n1 35\\n2 10\\n2 11\\n\", \"10\\n3 11\\n2 21\\n5 12\\n5 5\\n1 6\\n1 21\\n3 11\\n1 35\\n2 10\\n2 11\\n\", \"10\\n3 11\\n2 21\\n5 12\\n5 5\\n1 6\\n2 21\\n3 11\\n1 35\\n2 10\\n2 11\\n\", \"10\\n1 4\\n1 12\\n5 13\\n5 5\\n2 5\\n1 7\\n1 10\\n7 9\\n8 9\\n9 11\\n\", \"10\\n6 7\\n5 11\\n3 10\\n9 10\\n11 12\\n6 12\\n7 11\\n1 1\\n5 9\\n2 8\\n\", \"10\\n6 9\\n2 8\\n6 12\\n8 15\\n2 5\\n1 2\\n7 15\\n12 15\\n5 12\\n8 15\\n\", \"10\\n10 10\\n13 29\\n6 14\\n3 15\\n4 15\\n11 12\\n11 15\\n8 15\\n1 11\\n1 9\\n\", \"10\\n2 8\\n8 10\\n1 6\\n1 2\\n7 10\\n1 9\\n6 8\\n3 4\\n1 3\\n5 8\\n\", \"10\\n1 11\\n4 10\\n1 5\\n5 10\\n1 8\\n4 5\\n1 8\\n4 8\\n5 10\\n10 10\\n\", \"10\\n1 2\\n10 12\\n5 12\\n1 7\\n1 6\\n11 12\\n3 8\\n7 9\\n11 12\\n1 6\\n\", \"10\\n11 12\\n6 13\\n5 9\\n7 11\\n1 12\\n11 15\\n3 13\\n1 14\\n6 8\\n10 10\\n\", \"10\\n3 11\\n2 12\\n7 19\\n5 5\\n6 6\\n1 11\\n11 11\\n1 12\\n1 10\\n7 11\\n\", \"2\\n2 3\\n1 3\\n\", \"10\\n6 9\\n1 8\\n1 12\\n8 15\\n2 5\\n1 2\\n2 15\\n12 15\\n5 12\\n8 15\\n\", \"10\\n12 12\\n11 13\\n5 9\\n6 11\\n1 12\\n11 15\\n3 13\\n1 14\\n6 8\\n10 10\\n\", \"10\\n3 11\\n2 12\\n7 12\\n5 5\\n6 6\\n1 11\\n11 11\\n1 12\\n1 10\\n2 15\\n\", \"10\\n2 4\\n10 23\\n1 10\\n6 13\\n9 12\\n1 4\\n13 15\\n1 11\\n1 10\\n5 6\\n\", \"10\\n10 10\\n13 15\\n6 14\\n10 15\\n4 15\\n11 12\\n11 15\\n5 15\\n1 11\\n1 9\\n\", \"10\\n1 2\\n1 3\\n1 18\\n10 10\\n4 4\\n5 9\\n2 5\\n7 13\\n2 10\\n7 20\\n\", \"10\\n3 11\\n2 12\\n7 12\\n5 5\\n6 6\\n1 21\\n11 11\\n1 12\\n1 10\\n4 11\\n\", \"10\\n15 15\\n6 6\\n1 6\\n7 15\\n3 13\\n10 15\\n6 13\\n2 9\\n2 14\\n12 26\\n\", \"10\\n2 4\\n10 10\\n1 10\\n6 13\\n9 12\\n1 10\\n13 15\\n1 11\\n1 10\\n5 6\\n\", \"10\\n10 10\\n13 15\\n6 14\\n10 15\\n4 15\\n11 12\\n11 15\\n8 15\\n1 20\\n1 9\\n\", \"10\\n2 4\\n10 10\\n1 10\\n6 22\\n9 12\\n1 10\\n13 15\\n1 11\\n1 10\\n5 6\\n\", \"10\\n3 11\\n2 12\\n7 12\\n5 5\\n1 6\\n1 21\\n11 11\\n1 12\\n2 10\\n2 11\\n\", \"10\\n3 11\\n2 12\\n5 12\\n5 5\\n1 6\\n1 21\\n11 11\\n1 12\\n2 10\\n2 11\\n\", \"10\\n2 4\\n10 10\\n1 10\\n6 22\\n9 12\\n1 10\\n11 14\\n1 11\\n1 10\\n5 6\\n\", \"10\\n10 13\\n13 15\\n6 14\\n6 15\\n4 15\\n11 12\\n11 15\\n8 15\\n1 11\\n1 9\\n\", \"10\\n1 4\\n10 23\\n5 12\\n1 7\\n1 6\\n11 12\\n3 8\\n7 9\\n11 12\\n5 6\\n\", \"10\\n1 10\\n3 4\\n1 10\\n3 4\\n5 9\\n1 4\\n7 12\\n1 9\\n1 8\\n4 10\\n\", \"10\\n15 15\\n6 6\\n1 6\\n7 15\\n3 13\\n10 15\\n6 13\\n2 7\\n2 14\\n12 26\\n\", \"3\\n1 2\\n2 3\\n3 4\\n\", \"2\\n1 3\\n1 3\\n\"], \"outputs\": [\"1 10 4 6 5 7 8 9 2 3 \\n\", \"1 10 6 5 2 3 4 7 8 9 \", \"6 8 7 9 12 11 10 1 5 2 \\n\", \"6 3 7 9 2 1 8 12 5 10 \\n\", \"2 10 3 7 9 4 13 6 1 5 \\n\", \"10 13 6 3 4 11 12 8 2 1 \", \"1 2 5 10 4 6 3 7 8 9 \\n\", \"4 10 2 8 9 7 6 3 1 5 \\n\", \"2 7 1 8 3 4 5 6 9 10 \\n\", \"1 10 6 3 2 11 4 7 12 5 \\n\", \"12 8 5 7 1 11 3 2 6 10 \", \"7 3 10 4 6 1 9 5 2 8 \\n\", \"15 6 1 8 3 10 7 2 4 12 \", \"9 2 8 6 4 12 7 1 3 5 \\n\", \"3 8 9 5 6 2 11 4 1 7 \\n\", \"6 8 7 9 12 11 10 1 5 2\\n\", \"6 3 7 8 2 1 4 12 5 9\\n\", \"2 10 3 7 9 4 13 6 1 5\\n\", \"10 13 6 7 4 11 12 8 2 1\\n\", \"1 2 9 10 4 5 3 7 6 8\\n\", \"1 10 6 3 2 11 4 7 12 5\\n\", \"12 8 5 7 1 11 3 2 6 10\\n\", \"7 3 8 4 6 1 10 5 2 9\\n\", \"15 6 1 8 3 10 7 2 4 12\\n\", \"4 8 9 5 6 2 11 7 1 3\\n\", \"2 10 1 7 9 3 13 6 4 5\\n\", \"10 14 6 12 4 11 13 8 2 1\\n\", \"1 2 9 10 4 5 3 8 6 7\\n\", \"3 7 8 5 6 9 11 4 1 2\\n\", \"15 6 1 8 3 10 7 4 2 12\\n\", \"4 7 8 5 1 9 11 6 2 3\\n\", \"2 10 1 7 9 3 11 6 4 5\\n\", \"4 6 7 5 1 9 11 8 2 3\\n\", \"4 9 6 5 1 8 11 7 2 3\\n\", \"4 8 6 5 1 7 11 9 2 3\\n\", \"4 9 7 5 1 8 6 10 2 3\\n\", \"4 8 7 5 1 9 6 10 2 3\\n\", \"1 6 10 5 2 3 4 7 8 9\\n\", \"6 7 3 9 11 10 8 1 5 2\\n\", \"6 3 7 9 2 1 8 12 5 10\\n\", \"10 13 6 3 4 11 12 8 2 1\\n\", \"5 10 4 1 9 8 7 3 2 6\\n\", \"9 6 1 7 2 4 3 5 8 10\\n\", \"1 10 6 4 2 11 5 7 12 3\\n\", \"11 8 5 7 1 12 3 2 6 10\\n\", \"3 8 9 5 6 2 11 4 1 7\\n\", \"2 1\\n\", \"6 3 4 8 2 1 7 12 5 9\\n\", \"12 11 5 7 1 13 3 2 6 10\\n\", \"3 7 8 5 6 2 11 4 1 9\\n\", \"2 10 3 7 9 1 13 6 4 5\\n\", \"10 14 6 12 4 11 13 5 2 1\\n\", \"1 2 8 10 4 5 3 7 6 9\\n\", \"3 7 8 5 6 9 11 2 1 4\\n\", \"15 6 1 8 3 10 7 2 4 12\\n\", \"2 10 1 7 9 3 13 6 4 5\\n\", \"10 14 6 12 4 11 13 8 2 1\\n\", \"2 10 1 7 9 3 13 6 4 5\\n\", \"4 7 8 5 1 9 11 6 2 3\\n\", \"4 7 8 5 1 9 11 6 2 3\\n\", \"2 10 1 7 9 3 11 6 4 5\\n\", \"10 13 6 7 4 11 12 8 2 1\\n\", \"1 10 6 3 2 11 4 7 12 5\\n\", \"7 3 8 4 6 1 10 5 2 9\\n\", \"15 6 1 8 3 10 7 2 4 12\\n\", \"1 2 3 \", \"1 2 \"]}", "source": "taco"}
|
On a history lesson the teacher asked Vasya to name the dates when n famous events took place. He doesn't remembers the exact dates but he remembers a segment of days [li, ri] (inclusive) on which the event could have taken place. However Vasya also remembers that there was at most one event in one day. Help him choose such n dates of famous events that will fulfill both conditions. It is guaranteed that it is possible.
Input
The first line contains one integer n (1 ≤ n ≤ 100) — the number of known events. Then follow n lines containing two integers li and ri each (1 ≤ li ≤ ri ≤ 107) — the earliest acceptable date and the latest acceptable date of the i-th event.
Output
Print n numbers — the dates on which the events took place. If there are several solutions, print any of them. It is guaranteed that a solution exists.
Examples
Input
3
1 2
2 3
3 4
Output
1 2 3
Input
2
1 3
1 3
Output
1 2
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"160\\n1 1 4 0\\n160\\n1 0 2 10\\n0\", \"160\\n1 1 4 0\\n58\\n2 0 4 10\\n0\", \"160\\n1 1 4 0\\n46\\n2 0 4 10\\n0\", \"160\\n1 1 4 0\\n160\\n0 0 2 10\\n0\", \"160\\n1 1 2 0\\n160\\n1 -1 1 10\\n0\", \"160\\n1 1 4 0\\n109\\n2 0 7 10\\n0\", \"160\\n0 1 4 0\\n160\\n0 1 2 10\\n0\", \"160\\n1 1 4 0\\n46\\n2 1 1 10\\n0\", \"160\\n1 0 4 0\\n109\\n2 0 3 10\\n0\", \"160\\n1 0 4 0\\n46\\n2 1 1 10\\n0\", \"160\\n1 1 4 0\\n125\\n-1 1 2 10\\n0\", \"160\\n1 1 3 0\\n198\\n2 -1 0 16\\n0\", \"160\\n1 0 3 0\\n198\\n2 -1 0 16\\n0\", \"160\\n1 1 2 0\\n160\\n1 1 2 10\\n0\", \"160\\n2 0 4 1\\n83\\n1 0 4 5\\n0\", \"160\\n1 1 8 0\\n125\\n-1 1 2 10\\n0\", \"160\\n1 1 4 0\\n77\\n-1 2 2 10\\n0\", \"160\\n1 0 2 0\\n104\\n2 -1 -1 1\\n0\", \"160\\n1 0 4 0\\n160\\n2 0 2 6\\n0\", \"160\\n1 1 4 0\\n46\\n2 0 7 9\\n0\", \"160\\n1 1 4 1\\n46\\n5 0 4 10\\n0\", \"160\\n0 1 2 0\\n160\\n1 -1 2 5\\n0\", \"160\\n1 1 0 2\\n160\\n1 0 2 10\\n0\", \"160\\n1 1 4 0\\n109\\n2 0 14 5\\n0\", \"160\\n0 0 4 0\\n109\\n2 1 3 10\\n0\", \"160\\n2 2 6 1\\n86\\n1 0 4 5\\n0\", \"160\\n1 0 2 0\\n116\\n-1 1 2 10\\n0\", \"160\\n1 1 2 1\\n218\\n1 1 2 10\\n0\", \"160\\n1 1 4 1\\n26\\n5 0 4 10\\n0\", \"160\\n1 0 4 0\\n109\\n2 0 14 5\\n0\", \"160\\n1 1 2 1\\n218\\n1 1 0 10\\n0\", \"160\\n1 0 4 0\\n21\\n2 0 14 5\\n0\", \"160\\n0 -1 4 0\\n109\\n2 1 3 10\\n0\", \"160\\n0 1 2 0\\n238\\n2 -1 2 3\\n0\", \"160\\n2 1 0 2\\n160\\n0 -1 2 10\\n0\", \"160\\n0 1 2 0\\n5\\n0 1 1 18\\n0\", \"160\\n1 1 2 0\\n218\\n2 1 0 10\\n0\", \"160\\n1 1 7 0\\n107\\n2 0 7 9\\n0\", \"160\\n2 0 0 2\\n160\\n0 -1 2 10\\n0\", \"160\\n0 1 4 1\\n160\\n0 -1 3 2\\n0\", \"160\\n0 1 3 0\\n158\\n1 -2 0 11\\n0\", \"160\\n1 0 4 0\\n101\\n-1 2 0 3\\n0\", \"160\\n1 0 2 0\\n160\\n6 -1 2 0\\n0\", \"160\\n1 2 4 1\\n30\\n5 -1 4 10\\n0\", \"160\\n2 0 0 2\\n160\\n0 -1 3 10\\n0\", \"160\\n1 1 3 0\\n0\\n2 -1 0 31\\n0\", \"160\\n1 2 4 1\\n30\\n5 -1 7 10\\n0\", \"160\\n2 0 0 3\\n160\\n0 0 3 20\\n0\", \"160\\n1 2 1 1\\n30\\n5 0 7 13\\n0\", \"160\\n1 0 4 0\\n160\\n2 -1 7 2\\n0\", \"160\\n1 2 1 1\\n4\\n5 0 14 13\\n0\", \"160\\n2 0 5 0\\n0\\n6 -1 -1 62\\n0\", \"160\\n1 0 1 1\\n4\\n5 0 14 13\\n0\", \"160\\n1 0 4 0\\n160\\n1 -1 14 3\\n0\", \"160\\n1 0 4 0\\n317\\n1 -1 7 3\\n0\", \"160\\n2 0 5 1\\n1\\n6 -1 0 62\\n0\", \"160\\n0 0 0 2\\n4\\n1 0 14 0\\n0\", \"160\\n1 0 4 0\\n149\\n0 0 8 3\\n0\", \"160\\n1 0 4 0\\n149\\n0 0 14 3\\n0\", \"160\\n0 0 0 1\\n8\\n0 0 14 0\\n0\", \"160\\n1 1 4 0\\n149\\n0 0 14 3\\n0\", \"160\\n0 0 0 1\\n8\\n0 0 17 0\\n0\", \"160\\n0 1 4 0\\n149\\n0 0 14 3\\n0\", \"160\\n2 0 0 2\\n-1\\n1 0 0 112\\n0\", \"160\\n0 1 0 1\\n7\\n1 -1 17 1\\n0\", \"160\\n0 0 4 0\\n98\\n1 0 6 0\\n0\", \"160\\n0 1 2 2\\n7\\n1 -1 17 1\\n0\", \"160\\n1 1 2 2\\n7\\n1 -1 17 1\\n0\", \"160\\n1 1 0 2\\n7\\n1 -1 17 1\\n0\", \"160\\n1 1 0 1\\n7\\n1 -1 11 1\\n0\", \"160\\n1 1 4 0\\n167\\n2 0 3 10\\n0\", \"160\\n1 0 2 0\\n120\\n2 -1 -1 1\\n0\", \"160\\n2 0 4 1\\n83\\n1 0 6 5\\n0\", \"160\\n1 0 1 1\\n104\\n2 -1 -1 1\\n0\", \"160\\n1 1 4 0\\n46\\n2 1 7 9\\n0\", \"160\\n1 1 4 0\\n206\\n2 0 14 5\\n0\", \"160\\n2 -1 0 1\\n83\\n1 0 4 5\\n0\", \"160\\n1 1 8 0\\n1\\n-1 1 1 10\\n0\", \"160\\n0 0 2 0\\n116\\n-1 1 2 10\\n0\", \"160\\n0 1 4 1\\n26\\n5 0 4 10\\n0\", \"160\\n1 1 8 0\\n160\\n2 0 3 10\\n0\", \"160\\n1 0 4 0\\n109\\n1 0 7 10\\n0\", \"160\\n1 0 2 0\\n46\\n1 1 5 10\\n0\", \"160\\n1 1 7 0\\n109\\n2 0 14 5\\n0\", \"160\\n0 2 2 0\\n214\\n1 -1 1 3\\n0\", \"160\\n1 0 1 1\\n116\\n-1 1 2 10\\n0\", \"160\\n0 2 2 0\\n160\\n2 -1 2 3\\n0\", \"160\\n1 1 4 0\\n244\\n2 0 3 10\\n0\", \"160\\n2 1 6 0\\n160\\n1 -2 2 4\\n0\", \"160\\n0 2 2 0\\n5\\n0 1 1 18\\n0\", \"160\\n1 2 4 1\\n40\\n5 0 4 10\\n0\", \"160\\n0 1 2 0\\n10\\n0 0 1 18\\n0\", \"160\\n1 -1 4 1\\n109\\n3 2 3 10\\n0\", \"160\\n0 1 3 0\\n0\\n2 -1 0 31\\n0\", \"160\\n0 2 1 1\\n56\\n5 0 7 13\\n0\", \"160\\n2 1 6 0\\n0\\n4 -1 -1 62\\n0\", \"160\\n1 0 1 1\\n4\\n5 0 28 13\\n0\", \"160\\n1 0 1 2\\n4\\n1 0 9 0\\n0\", \"160\\n1 0 4 0\\n149\\n0 0 4 3\\n0\", \"160\\n2 0 7 1\\n0\\n1 -1 0 112\\n0\", \"160\\n1 1 2 0\\n160\\n1 0 2 10\\n0\"], \"outputs\": [\"10 1\\n50 1\\n100 1\\n\\n10 1\\n100 2\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 1\\n100 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n100 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n100 2\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 1\\n500 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 1\\n100 6\\n\", \"100 2\\n\\n100 2\\n\", \"10 1\\n50 1\\n100 1\\n\\n50 1\\n\", \"10 1\\n100 2\\n\\n10 1\\n100 1\\n\", \"10 1\\n100 2\\n\\n50 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n50 1\\n100 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n500 1\\n\", \"10 1\\n100 2\\n\\n500 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 1\\n50 1\\n100 1\\n\", \"10 1\\n100 2\\n\\n100 1\\n\", \"10 1\\n50 1\\n100 6\\n\\n50 1\\n100 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n50 2\\n\", \"10 1\\n100 2\\n\\n10 1\\n500 1\\n\", \"10 1\\n100 2\\n\\n10 1\\n100 2\\n\", \"10 1\\n50 1\\n100 1\\n\\n100 6\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 5\\n\", \"100 2\\n\\n10 1\\n100 2\\n\", \"10 1\\n50 1\\n500 1\\n\\n10 1\\n100 2\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 1\\n100 11\\n\", \"100 2\\n\\n10 1\\n100 1\\n\", \"10 1\\n50 1\\n100 6\\n\\n100 1\\n\", \"10 1\\n100 2\\n\\n50 1\\n100 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n50 1\\n100 2\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 3\\n\", \"10 1\\n100 2\\n\\n10 1\\n100 11\\n\", \"10 1\\n50 1\\n100 1\\n\\n50 1\\n500 1\\n\", \"10 1\\n100 2\\n\\n100 11\\n\", \"100 3\\n\\n10 1\\n100 1\\n\", \"100 2\\n\\n500 1\\n\", \"10 1\\n50 1\\n500 1\\n\\n500 1\\n\", \"100 2\\n\\n50 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 2\\n500 1\\n\", \"10 1\\n50 1\\n100 6\\n\\n10 1\\n100 6\\n\", \"10 1\\n500 1\\n\\n500 1\\n\", \"100 2\\n\\n100 3\\n\", \"100 2\\n\\n10 1\\n500 1\\n\", \"10 1\\n100 2\\n\\n50 1\\n500 1\\n\", \"10 1\\n100 2\\n\\n10 6\\n100 2\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 3\\n100 1\\n\", \"10 1\\n500 1\\n\\n100 3\\n\", \"10 1\\n50 1\\n100 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 3\\n100 6\\n\", \"10 1\\n500 1\\n\\n100 2\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 3\\n100 5\\n\", \"10 1\\n100 2\\n\\n10 1\\n100 7\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 1\\n100 10\\n\", \"10 1\\n100 2\\n\", \"10 1\\n500 1\\n\\n10 1\\n100 10\\n\", \"10 1\\n100 2\\n\\n10 1\\n100 12\\n\", \"10 1\\n100 2\\n\\n100 4\\n\", \"10 1\\n100 2\\n\\n10 6\\n\", \"500 1\\n\\n10 1\\n100 10\\n\", \"10 1\\n100 2\\n\\n100 7\\n\", \"10 1\\n100 2\\n\\n100 12\\n\", \"500 1\\n\\n100 11\\n\", \"10 1\\n50 1\\n100 1\\n\\n100 12\\n\", \"500 1\\n\\n100 16\\n\", \"100 2\\n\\n100 12\\n\", \"10 1\\n500 1\\n\\n\", \"500 1\\n\\n10 1\\n100 16\\n\", \"100 2\\n\\n100 6\\n\", \"100 2\\n\\n10 1\\n100 16\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 1\\n100 16\\n\", \"10 1\\n50 1\\n500 1\\n\\n10 1\\n100 16\\n\", \"10 1\\n50 1\\n500 1\\n\\n10 1\\n100 11\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 2\\n100 2\\n\", \"10 1\\n100 2\\n\\n10 2\\n500 1\\n\", \"10 1\\n100 2\\n\\n100 6\\n\", \"10 1\\n500 1\\n\\n10 1\\n500 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n50 1\\n100 5\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 1\\n100 12\\n\", \"10 1\\n500 1\\n\\n100 1\\n\", \"10 1\\n50 1\\n100 6\\n\\n50 1\\n\", \"100 2\\n\\n50 1\\n100 1\\n\", \"100 2\\n\\n10 3\\n\", \"10 1\\n50 1\\n100 6\\n\\n10 1\\n100 2\\n\", \"10 1\\n100 2\\n\\n10 1\\n100 6\\n\", \"10 1\\n100 2\\n\\n50 1\\n100 5\\n\", \"10 1\\n50 1\\n100 6\\n\\n10 1\\n100 11\\n\", \"50 2\\n100 1\\n\\n500 1\\n\", \"10 1\\n500 1\\n\\n50 1\\n100 1\\n\", \"50 2\\n100 1\\n\\n10 1\\n100 2\\n\", \"10 1\\n50 1\\n100 1\\n\\n100 3\\n\", \"10 1\\n50 1\\n100 6\\n\\n10 1\\n500 1\\n\", \"50 2\\n100 1\\n\\n50 1\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 4\\n\", \"100 2\\n\\n100 1\\n\", \"10 1\\n100 2\\n\\n10 1\\n50 2\\n\", \"100 2\\n\", \"50 2\\n100 1\\n\\n10 1\\n100 6\\n\", \"10 1\\n50 1\\n100 6\\n\", \"10 1\\n500 1\\n\\n10 1\\n100 25\\n\", \"10 1\\n500 1\\n\\n10 1\\n100 5\\n\", \"10 1\\n100 2\\n\\n100 2\\n\", \"10 1\\n100 7\\n\", \"10 1\\n50 1\\n100 1\\n\\n10 1\\n100 2\"]}", "source": "taco"}
|
Mr. Bill is shopping at the store. There are some coins in his wallet (10-yen coins, 50-yen coins, 100-yen coins, 500-yen coins), but he is now trying to consume as much of this coin as possible. In other words, by paying for the goods with an appropriate number of coins, we are trying to minimize the total number of coins after receiving the change.
Fortunately, the clerk at this store is so disciplined and kind that change is always delivered in the best possible way. Therefore, for example, five 100-yen coins will not be given instead of one 500-yen coin. You can also take out 5 10-yen coins and receive 50-yen coins as change. However, you must not pay the coins of the same type as the coins you issued so that they will be returned as change. For example, if a 10-yen coin is paid out and another 10-yen coin is returned as change, a completely meaningless exchange will occur.
However, Mr. Bill was not good at calculating, so he could not find out how many coins he should actually use. So he asked you for help. Your job is to write a program to determine the type and number of coins to use based on the number of coins in his wallet and the payment price. The clerk does not use banknotes for change.
Input
The input contains several test cases.
Each test case consists of two lines. The first line contains a single integer representing Mr. Bill's payment in yen. The second line contains four integers, which in turn represent the number of 10-yen coins, 50-yen coins, 100-yen coins, and 500-yen coins in your wallet.
The payment amount is always in units of 10 yen. That is, the one-yen place of the payment amount is always 0. You can also assume that you can only have up to 20 coins of the same type in your wallet. No non-payable cases are given during input.
The end of input is represented by a line containing a single 0.
Output
For each test case, print out the type and number of coins that Mr. Bill should use.
Each line of output contains the two integers ci and ki. This means using ki coins for ci yen when paying. When using multiple types of coins, output as many lines as necessary in order from the smallest ci. Refer to the output example below.
The output must not include extra space. Separate consecutive test cases with a blank line.
Example
Input
160
1 1 2 0
160
1 0 2 10
0
Output
10 1
50 1
100 1
10 1
100 2
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\\n2 1 3\\n\", \"3\\n3 1 4\\n\", \"1\\n1\\n\", \"4\\n7 7 1 1\\n\", \"2\\n3 4\\n\", \"10\\n582366931603099761 314858607473442114 530263190370309150 871012489649491233 877068367969362781 671646356752418008 390155369686708364 958695211216189893 919124874293325142 196726357117434998\\n\", \"20\\n541032394951352952 204302388514120798 548305186805250399 743987576790520671 332874928746186630 60150973547887825 600093435051546090 862815570651991829 798946884837606574 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 249026359394730496 113333959133237279\\n\", \"5\\n634519819680016938 145747338084304007 736584718256570626 192864787402536196 542499811257052067\\n\", \"2\\n3 4\\n\", \"10\\n582366931603099761 314858607473442114 530263190370309150 871012489649491233 877068367969362781 671646356752418008 390155369686708364 958695211216189893 919124874293325142 196726357117434998\\n\", \"20\\n541032394951352952 204302388514120798 548305186805250399 743987576790520671 332874928746186630 60150973547887825 600093435051546090 862815570651991829 798946884837606574 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 249026359394730496 113333959133237279\\n\", \"5\\n634519819680016938 145747338084304007 736584718256570626 192864787402536196 542499811257052067\\n\", \"2\\n4 4\\n\", \"10\\n582366931603099761 314858607473442114 530263190370309150 871012489649491233 877068367969362781 671646356752418008 390155369686708364 958695211216189893 1349432255127981997 196726357117434998\\n\", \"20\\n541032394951352952 204302388514120798 548305186805250399 743987576790520671 33957332510720084 60150973547887825 600093435051546090 862815570651991829 798946884837606574 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 249026359394730496 113333959133237279\\n\", \"5\\n634519819680016938 226891651314082218 736584718256570626 192864787402536196 542499811257052067\\n\", \"3\\n0 1 4\\n\", \"4\\n7 7 1 2\\n\", \"3\\n2 1 2\\n\", \"3\\n0 1 1\\n\", \"4\\n7 11 1 2\\n\", \"5\\n634519819680016938 226891651314082218 736584718256570626 265468079440238573 182525869678133414\\n\", \"10\\n582366931603099761 21907772642571758 647480728913150925 871012489649491233 877068367969362781 438338154910289406 390155369686708364 958695211216189893 1349432255127981997 243851770570733450\\n\", \"5\\n756949526263187099 226891651314082218 736584718256570626 265468079440238573 182525869678133414\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 871012489649491233 877068367969362781 438338154910289406 390155369686708364 958695211216189893 1349432255127981997 243851770570733450\\n\", \"20\\n541032394951352952 204302388514120798 548305186805250399 743987576790520671 33957332510720084 60716857992873480 600093435051546090 416411540235413810 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 394531838370790018 80168296772623859\\n\", \"5\\n756949526263187099 226891651314082218 32908436120352344 265468079440238573 182525869678133414\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 871012489649491233 259943388022277986 438338154910289406 390155369686708364 334787340433657516 1349432255127981997 243851770570733450\\n\", \"20\\n541032394951352952 92209649804419534 548305186805250399 743987576790520671 33957332510720084 60716857992873480 600093435051546090 416411540235413810 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 365327974066443412 80168296772623859\\n\", \"5\\n756949526263187099 226891651314082218 57080436999102121 265468079440238573 142558439574463303\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 871012489649491233 259943388022277986 438338154910289406 390155369686708364 334787340433657516 1212155644642845052 243851770570733450\\n\", \"5\\n756949526263187099 35694444483417993 108806667016466936 265468079440238573 142558439574463303\\n\", \"5\\n756949526263187099 58105730574618160 108806667016466936 265468079440238573 142558439574463303\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 871012489649491233 18659981377050541 438338154910289406 390155369686708364 334787340433657516 1352043575491439785 243851770570733450\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 871012489649491233 18659981377050541 438338154910289406 199095890033722229 334787340433657516 1352043575491439785 243851770570733450\\n\", \"5\\n756949526263187099 58105730574618160 167018603849153818 265468079440238573 165052020503177632\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 871012489649491233 18659981377050541 438338154910289406 199095890033722229 334787340433657516 1352043575491439785 32933308082844947\\n\", \"5\\n756949526263187099 58105730574618160 167018603849153818 369748668069417141 165052020503177632\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 1104028854603887863 18659981377050541 438338154910289406 199095890033722229 334787340433657516 1352043575491439785 32933308082844947\\n\", \"5\\n756949526263187099 58105730574618160 167018603849153818 374672612061882444 165052020503177632\\n\", \"4\\n0 10 0 0\\n\", \"4\\n0 10 0 1\\n\", \"10\\n286580504249349949 21907772642571758 647480728913150925 101030237167530479 18659981377050541 438338154910289406 605749649019647 334787340433657516 1352043575491439785 32933308082844947\\n\", \"4\\n0 13 0 1\\n\", \"10\\n286580504249349949 21907772642571758 884017053637536954 101030237167530479 18659981377050541 438338154910289406 605749649019647 334787340433657516 1352043575491439785 32933308082844947\\n\", \"5\\n756949526263187099 58105730574618160 361818831453278637 671915973155547380 5744103650824997\\n\", \"5\\n756949526263187099 58105730574618160 361818831453278637 646488303858664586 5744103650824997\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 39782112198538546 60716857992873480 186511716026383547 416411540235413810 87507855731056509 383607230476788640 1340866670397321723 160052615724629523 824508576221039025 547099154391774856 24650799315436599 650099395201051981 318873920071434596 655488876699739456 365327974066443412 80168296772623859\\n\", \"2\\n4 7\\n\", \"10\\n582366931603099761 314858607473442114 530263190370309150 871012489649491233 877068367969362781 438338154910289406 390155369686708364 958695211216189893 1349432255127981997 196726357117434998\\n\", \"20\\n541032394951352952 204302388514120798 548305186805250399 743987576790520671 33957332510720084 60150973547887825 600093435051546090 862815570651991829 798946884837606574 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 394531838370790018 113333959133237279\\n\", \"5\\n634519819680016938 226891651314082218 736584718256570626 289717660832367635 542499811257052067\\n\", \"3\\n2 1 1\\n\", \"2\\n0 7\\n\", \"10\\n582366931603099761 314858607473442114 530263190370309150 871012489649491233 877068367969362781 438338154910289406 390155369686708364 958695211216189893 1349432255127981997 243851770570733450\\n\", \"20\\n541032394951352952 204302388514120798 548305186805250399 743987576790520671 33957332510720084 60150973547887825 600093435051546090 862815570651991829 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 394531838370790018 113333959133237279\\n\", \"5\\n634519819680016938 226891651314082218 736584718256570626 265468079440238573 542499811257052067\\n\", \"3\\n0 0 1\\n\", \"4\\n7 11 1 3\\n\", \"3\\n0 1 2\\n\", \"10\\n582366931603099761 21907772642571758 530263190370309150 871012489649491233 877068367969362781 438338154910289406 390155369686708364 958695211216189893 1349432255127981997 243851770570733450\\n\", \"20\\n541032394951352952 204302388514120798 548305186805250399 743987576790520671 33957332510720084 60150973547887825 600093435051546090 862815570651991829 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 394531838370790018 80168296772623859\\n\", \"4\\n7 15 1 3\\n\", \"3\\n0 1 0\\n\", \"20\\n541032394951352952 204302388514120798 548305186805250399 743987576790520671 33957332510720084 60716857992873480 600093435051546090 862815570651991829 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 394531838370790018 80168296772623859\\n\", \"4\\n7 15 2 3\\n\", \"4\\n7 15 0 3\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 871012489649491233 259943388022277986 438338154910289406 390155369686708364 958695211216189893 1349432255127981997 243851770570733450\\n\", \"20\\n541032394951352952 204302388514120798 548305186805250399 743987576790520671 33957332510720084 60716857992873480 600093435051546090 416411540235413810 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 411018774272655732 824285680939035203 163645155990193908 655488876699739456 365327974066443412 80168296772623859\\n\", \"5\\n756949526263187099 226891651314082218 32908436120352344 265468079440238573 142558439574463303\\n\", \"4\\n5 15 1 3\\n\", \"4\\n5 15 1 4\\n\", \"20\\n541032394951352952 92209649804419534 548305186805250399 743987576790520671 33957332510720084 60716857992873480 600093435051546090 416411540235413810 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 348158551088716173 824285680939035203 163645155990193908 655488876699739456 365327974066443412 80168296772623859\\n\", \"5\\n756949526263187099 226891651314082218 108806667016466936 265468079440238573 142558439574463303\\n\", \"4\\n7 15 1 4\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 871012489649491233 16030950320653174 438338154910289406 390155369686708364 334787340433657516 1212155644642845052 243851770570733450\\n\", \"20\\n541032394951352952 92209649804419534 548305186805250399 743987576790520671 33957332510720084 60716857992873480 600093435051546090 416411540235413810 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 348158551088716173 650099395201051981 163645155990193908 655488876699739456 365327974066443412 80168296772623859\\n\", \"4\\n0 15 1 4\\n\", \"10\\n273911769131190750 21907772642571758 647480728913150925 871012489649491233 18659981377050541 438338154910289406 390155369686708364 334787340433657516 1212155644642845052 243851770570733450\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 33957332510720084 60716857992873480 600093435051546090 416411540235413810 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 348158551088716173 650099395201051981 163645155990193908 655488876699739456 365327974066443412 80168296772623859\\n\", \"4\\n0 15 0 4\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 33957332510720084 60716857992873480 600093435051546090 416411540235413810 360387394696939166 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 525688784247989880 650099395201051981 163645155990193908 655488876699739456 365327974066443412 80168296772623859\\n\", \"5\\n756949526263187099 58105730574618160 167018603849153818 265468079440238573 142558439574463303\\n\", \"4\\n0 4 0 4\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 33957332510720084 60716857992873480 600093435051546090 416411540235413810 134161510692954562 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 525688784247989880 650099395201051981 163645155990193908 655488876699739456 365327974066443412 80168296772623859\\n\", \"4\\n0 4 0 0\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 39782112198538546 60716857992873480 600093435051546090 416411540235413810 134161510692954562 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 525688784247989880 650099395201051981 163645155990193908 655488876699739456 365327974066443412 80168296772623859\\n\", \"4\\n0 3 0 0\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 39782112198538546 60716857992873480 600093435051546090 416411540235413810 134161510692954562 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 525688784247989880 650099395201051981 318873920071434596 655488876699739456 365327974066443412 80168296772623859\\n\", \"4\\n0 5 0 0\\n\", \"10\\n286580504249349949 21907772642571758 647480728913150925 1104028854603887863 18659981377050541 438338154910289406 199095890033722229 334787340433657516 1352043575491439785 32933308082844947\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 39782112198538546 60716857992873480 600093435051546090 416411540235413810 111537958776228507 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 525688784247989880 650099395201051981 318873920071434596 655488876699739456 365327974066443412 80168296772623859\\n\", \"5\\n756949526263187099 58105730574618160 225633679875520738 374672612061882444 165052020503177632\\n\", \"10\\n286580504249349949 21907772642571758 647480728913150925 1104028854603887863 18659981377050541 438338154910289406 605749649019647 334787340433657516 1352043575491439785 32933308082844947\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 39782112198538546 60716857992873480 600093435051546090 416411540235413810 87507855731056509 383607230476788640 748981752333005915 317959714195378963 824508576221039025 547099154391774856 525688784247989880 650099395201051981 318873920071434596 655488876699739456 365327974066443412 80168296772623859\\n\", \"5\\n756949526263187099 58105730574618160 361818831453278637 374672612061882444 165052020503177632\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 39782112198538546 60716857992873480 600093435051546090 416411540235413810 87507855731056509 383607230476788640 748981752333005915 160052615724629523 824508576221039025 547099154391774856 525688784247989880 650099395201051981 318873920071434596 655488876699739456 365327974066443412 80168296772623859\\n\", \"5\\n756949526263187099 58105730574618160 361818831453278637 374672612061882444 5744103650824997\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 39782112198538546 60716857992873480 600093435051546090 416411540235413810 87507855731056509 383607230476788640 748981752333005915 160052615724629523 824508576221039025 547099154391774856 24650799315436599 650099395201051981 318873920071434596 655488876699739456 365327974066443412 80168296772623859\\n\", \"4\\n0 13 1 1\\n\", \"10\\n286580504249349949 21907772642571758 884017053637536954 101030237167530479 18659981377050541 438338154910289406 605749649019647 558462591580521025 1352043575491439785 32933308082844947\\n\", \"20\\n365173133932353452 92209649804419534 548305186805250399 743987576790520671 39782112198538546 60716857992873480 186511716026383547 416411540235413810 87507855731056509 383607230476788640 748981752333005915 160052615724629523 824508576221039025 547099154391774856 24650799315436599 650099395201051981 318873920071434596 655488876699739456 365327974066443412 80168296772623859\\n\", \"4\\n0 13 2 1\\n\", \"10\\n286580504249349949 21907772642571758 884017053637536954 29582394911763778 18659981377050541 438338154910289406 605749649019647 558462591580521025 1352043575491439785 32933308082844947\\n\", \"3\\n3 1 4\\n\", \"4\\n7 7 1 1\\n\", \"1\\n1\\n\", \"3\\n2 1 3\\n\"], \"outputs\": [\"3\", \"7\", \"1\", \"7\", \"7\", \"1152921229728939135\", \"1152921504606842807\", \"1152886312701520811\", \"7\\n\", \"1152921229728939135\\n\", \"1152921504606842807\\n\", \"1152886312701520811\\n\", \"4\\n\", \"2305843009205305343\\n\", \"1152921504605797887\\n\", \"1152886312701520811\\n\", \"5\\n\", \"7\\n\", \"3\\n\", \"1\\n\", \"15\\n\", \"864691058913574895\\n\", \"2305843007594414077\\n\", \"846676729677207551\\n\", \"2305842458384121855\\n\", \"1152921504606845939\\n\", \"864686592969537535\\n\", \"2305690725242605567\\n\", \"1152921504571194227\\n\", \"864548146843478015\\n\", \"2303157997456588799\\n\", \"864691128455124991\\n\", \"864550390963761151\\n\", \"2305699522937863597\\n\", \"2303448272871620523\\n\", \"864550253259390975\\n\", \"2296692323674598911\\n\", \"1148980843826380735\\n\", \"2305698423434100735\\n\", \"1152780629408345855\\n\", \"10\\n\", \"11\\n\", \"2233644127929479149\\n\", \"13\\n\", \"2305825382658998207\\n\", \"1141515033203310591\\n\", \"1152351957314295743\\n\", \"2305842966264020479\\n\", \"7\\n\", \"2305843009205305343\\n\", \"1152921504605797887\\n\", \"1152886312701520811\\n\", \"3\\n\", \"7\\n\", \"2305843009205305343\\n\", \"1152921504605797887\\n\", \"1152886312701520811\\n\", \"1\\n\", \"15\\n\", \"3\\n\", \"2305843009205305343\\n\", \"1152921504605797887\\n\", \"15\\n\", \"1\\n\", \"1152921504605797887\\n\", \"15\\n\", \"15\\n\", \"2305842458384121855\\n\", \"1152921504605797887\\n\", \"864686592969537535\\n\", \"15\\n\", \"15\\n\", \"1152921504571194227\\n\", \"864548146843478015\\n\", \"15\\n\", \"2303157997456588799\\n\", \"1152921504605797887\\n\", \"15\\n\", \"2303157997456588799\\n\", \"1152921504605797887\\n\", \"15\\n\", \"1152921504605797887\\n\", \"864550390963761151\\n\", \"4\\n\", \"1152921504605797887\\n\", \"4\\n\", \"1152921504605797887\\n\", \"3\\n\", \"1152921504605797887\\n\", \"5\\n\", \"2305698423434100735\\n\", \"1152921504605797887\\n\", \"1152780629408345855\\n\", \"2305698423434100735\\n\", \"1152921504605797887\\n\", \"1152780629408345855\\n\", \"1152921504605797887\\n\", \"1152780629408345855\\n\", \"1152921504605797887\\n\", \"13\\n\", \"2305825382658998207\\n\", \"1152921504605797887\\n\", \"15\\n\", \"2305825382658998207\\n\", \"7\\n\", \"7\\n\", \"1\\n\", \"3\\n\"]}", "source": "taco"}
|
Ridhiman challenged Ashish to find the maximum valued subsequence of an array $a$ of size $n$ consisting of positive integers.
The value of a non-empty subsequence of $k$ elements of $a$ is defined as $\sum 2^i$ over all integers $i \ge 0$ such that at least $\max(1, k - 2)$ elements of the subsequence have the $i$-th bit set in their binary representation (value $x$ has the $i$-th bit set in its binary representation if $\lfloor \frac{x}{2^i} \rfloor \mod 2$ is equal to $1$).
Recall that $b$ is a subsequence of $a$, if $b$ can be obtained by deleting some(possibly zero) elements from $a$.
Help Ashish find the maximum value he can get by choosing some subsequence of $a$.
-----Input-----
The first line of the input consists of a single integer $n$ $(1 \le n \le 500)$ — the size of $a$.
The next line consists of $n$ space-separated integers — the elements of the array $(1 \le a_i \le 10^{18})$.
-----Output-----
Print a single integer — the maximum value Ashish can get by choosing some subsequence of $a$.
-----Examples-----
Input
3
2 1 3
Output
3
Input
3
3 1 4
Output
7
Input
1
1
Output
1
Input
4
7 7 1 1
Output
7
-----Note-----
For the first test case, Ashish can pick the subsequence $\{{2, 3}\}$ of size $2$. The binary representation of $2$ is 10 and that of $3$ is 11. Since $\max(k - 2, 1)$ is equal to $1$, the value of the subsequence is $2^0 + 2^1$ (both $2$ and $3$ have $1$-st bit set in their binary representation and $3$ has $0$-th bit set in its binary representation). Note that he could also pick the subsequence $\{{3\}}$ or $\{{2, 1, 3\}}$.
For the second test case, Ashish can pick the subsequence $\{{3, 4\}}$ with value $7$.
For the third test case, Ashish can pick the subsequence $\{{1\}}$ with value $1$.
For the fourth test case, Ashish can pick the subsequence $\{{7, 7\}}$ with value $7$.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\", \"100010\", \"6\", \"110010\", \"9\", \"110011\", \"11\", \"110001\", \"13\", \"111001\", \"26\", \"101001\", \"12\", \"101101\", \"8\", \"101100\", \"14\", \"101000\", \"21\", \"111000\", \"10\", \"111011\", \"28\", \"011011\", \"7\", \"011111\", \"15\", \"111111\", \"111110\", \"101110\", \"001110\", \"001111\", \"001100\", \"001000\", \"001001\", \"001101\", \"111100\", \"110100\", \"010100\", \"100100\", \"100101\", \"100111\", \"100110\", \"17\", \"110000\", \"101010\", \"010010\", \"16\", \"110111\", \"33\", \"011000\", \"010000\", \"37\", \"011001\", \"22\", \"111101\", \"24\", \"110110\", \"44\", \"010001\", \"011010\", \"101111\", \"54\", \"010011\", \"42\", \"011110\", \"52\", \"111010\", \"011101\", \"100001\", \"000110\", \"000111\", \"101011\", \"010101\", \"000101\", \"000100\", \"011100\", \"110101\", \"001011\", \"100011\", \"010111\", \"001010\", \"010110\", \"25\", \"43\", \"23\", \"34\", \"31\", \"97\", \"80\", \"51\", \"41\", \"56\", \"79\", \"20\", \"19\", \"93\", \"39\", \"84\", \"29\", \"2\", \"4\", \"5\", \"100000\"], \"outputs\": [\"4\\n\", \"795416653\\n\", \"516\\n\", \"993165555\\n\", \"275040\\n\", \"471359203\\n\", \"31000320\\n\", \"428910207\\n\", \"928152292\\n\", \"293611143\\n\", \"519834133\\n\", \"186012357\\n\", \"375736320\\n\", \"187749075\\n\", \"30096\\n\", \"984438011\\n\", \"545951517\\n\", \"202882297\\n\", \"480643881\\n\", \"900658160\\n\", \"2786400\\n\", \"852124128\\n\", \"160602026\\n\", \"552548279\\n\", \"3696\\n\", \"150919297\\n\", \"726290250\\n\", \"683412977\\n\", \"442822407\\n\", \"372082504\\n\", \"858201943\\n\", \"149188576\\n\", \"704619841\\n\", \"304547613\\n\", \"341392910\\n\", \"323131631\\n\", \"180661981\\n\", \"435389918\\n\", \"692628461\\n\", \"503475491\\n\", \"766869751\\n\", \"821954462\\n\", \"815833244\\n\", \"836297386\\n\", \"652946584\\n\", \"264910865\\n\", \"605503480\\n\", \"52284746\\n\", \"383313586\\n\", \"811739323\\n\", \"821839830\\n\", \"384714022\\n\", \"522039196\\n\", \"826755664\\n\", \"489224183\\n\", \"266370797\\n\", \"394392587\\n\", \"293060958\\n\", \"314992882\\n\", \"456499946\\n\", \"211970838\\n\", \"610693926\\n\", \"641739549\\n\", \"917055353\\n\", \"902356219\\n\", \"519764416\\n\", \"440189810\\n\", \"707668411\\n\", \"492291737\\n\", \"164851268\\n\", \"797167101\\n\", \"423942511\\n\", \"355691231\\n\", \"576690992\\n\", \"383267580\\n\", \"443017709\\n\", \"954483945\\n\", \"844199646\\n\", \"626332957\\n\", \"362392640\\n\", \"654104999\\n\", \"223883018\\n\", \"3678497\\n\", \"717197359\\n\", \"660702640\\n\", \"790454087\\n\", \"687288725\\n\", \"503939947\\n\", \"714607278\\n\", \"749297803\\n\", \"764662538\\n\", \"854808922\\n\", \"786429215\\n\", \"384578303\\n\", \"533305211\\n\", \"331538263\\n\", \"675151043\\n\", \"40943220\\n\", \"381015586\\n\", \"651702694\\n\", \"1\", \"16\", \"84\", \"341429644\"]}", "source": "taco"}
|
There are N squares lining up in a row, numbered 1 through N from left to right. Initially, all squares are white. We also have N-1 painting machines, numbered 1 through N-1. When operated, Machine i paints Square i and i+1 black.
Snuke will operate these machines one by one. The order in which he operates them is represented by a permutation of (1, 2, ..., N-1), P, which means that the i-th operated machine is Machine P_i.
Here, the score of a permutation P is defined as the number of machines that are operated before all the squares are painted black for the first time, when the machines are operated in the order specified by P. Snuke has not decided what permutation P to use, but he is interested in the scores of possible permutations. Find the sum of the scores over all possible permutations for him. Since this can be extremely large, compute the sum modulo 10^9+7.
Constraints
* 2 \leq N \leq 10^6
Input
Input is given from Standard Input in the following format:
N
Output
Print the sum of the scores over all possible permutations, modulo 10^9+7.
Examples
Input
4
Output
16
Input
2
Output
1
Input
5
Output
84
Input
100000
Output
341429644
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"5\\n10 0 -7 2 6\\n\", \"7\\n0 0 1 -1 0 0 2\\n\", \"5\\n0 0 0 1 1\\n\", \"1\\n777\\n\", \"2\\n1 0\\n\", \"100\\n39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39\\n\", \"100\\n-322 -198 -448 -249 -935 614 67 -679 -616 430 -71 818 -595 -22 559 -575 -710 50 -542 -144 -977 672 -826 -927 457 518 603 -287 689 -45 -770 208 360 -498 -884 -161 -831 -793 -991 -102 -706 338 298 -897 236 567 -22 577 -77 -481 376 -152 861 559 190 -662 432 -880 -839 737 857 -614 -670 -423 -320 -451 -733 -304 822 -316 52 46 -438 -427 601 -885 -644 518 830 -517 719 643 216 45 -15 382 411 -424 -649 286 -265 -49 704 661 -2 -992 67 -118 299 -420\\n\", \"100\\n621 862 494 -906 906 359 776 0 23 -868 863 -872 273 182 414 675 31 555 0 -423 468 517 577 892 117 664 292 11 105 589 173 455 711 358 229 -666 192 758 6 858 208 628 532 21 69 319 926 988 0 0 0 229 351 708 287 949 429 895 369 0 756 486 2 525 656 -906 742 284 174 510 747 227 274 103 50 -832 656 627 883 -603 927 989 797 463 615 798 832 535 562 517 194 697 661 176 814 -62 0 -886 239 221\\n\", \"10\\n-62 0 94 -49 84 -11 -88 0 -88 94\\n\", \"20\\n74 33 43 41 -83 -30 0 -20 84 99 83 0 64 0 57 46 0 18 94 82\\n\", \"20\\n-892 0 -413 742 0 0 754 23 -515 -293 0 918 -711 -362 -15 -776 -442 -902 116 732\\n\", \"20\\n355 -184 -982 -685 581 139 249 -352 -856 -436 679 397 653 325 -639 -722 769 345 -207 -632\\n\", \"50\\n40 -84 25 0 21 44 96 2 -49 -15 -58 58 0 -49 4 8 13 28 -78 69 0 35 43 0 41 97 99 0 0 5 71 58 10 15 0 30 49 0 -66 15 64 -51 0 50 0 23 43 -43 15 6\\n\", \"50\\n-657 0 -595 -527 -354 718 919 -770 -775 943 -23 0 -428 -322 -68 -429 -784 -981 -294 -260 533 0 0 -96 -839 0 -981 187 248 -56 -557 0 510 -824 -850 -531 -92 386 0 -952 519 -417 811 0 -934 -495 -813 -810 -733 0\\n\", \"50\\n-321 -535 -516 -822 -622 102 145 -607 338 -849 -499 892 -23 -120 40 -864 -452 -641 -902 41 745 -291 887 -175 -288 -69 -590 370 -421 195 904 558 886 89 -764 -378 276 -21 -531 668 872 88 -32 -558 230 181 -639 364 -940 177\\n\", \"50\\n-335 775 108 -928 -539 408 390 500 867 951 301 -113 -711 827 -83 422 -465 -355 -891 -957 -261 -507 930 385 745 198 238 33 805 -956 154 627 812 -518 216 785 817 -965 -916 999 986 718 55 698 -864 512 322 442 188 771\\n\", \"50\\n-306 -646 -572 -364 -706 796 900 -715 -808 -746 -49 -320 983 -414 -996 659 -439 -280 -913 126 -229 427 -493 -316 -831 -292 -942 707 -685 -82 654 490 -313 -660 -960 971 383 430 -145 -689 -757 -811 656 -419 244 203 -605 -287 44 -583\\n\", \"100\\n41 95 -57 5 -37 -58 61 0 59 42 45 64 35 84 11 53 5 -73 99 0 59 68 82 32 50 0 92 0 17 0 -2 82 86 -63 96 -7 0 0 -6 -86 96 88 81 82 0 41 9 0 67 88 80 84 78 0 16 66 0 17 56 46 82 0 11 -79 53 0 -94 73 12 93 30 75 89 0 56 90 79 -39 45 -18 38 52 82 8 -30 0 69 50 22 0 41 0 0 33 17 8 97 79 30 59\\n\", \"100\\n0 -927 -527 -306 -667 -229 -489 -194 -701 0 180 -723 0 3 -857 -918 -217 -471 732 -712 329 -40 0 0 -86 -820 -149 636 -260 -974 0 732 764 -769 916 -489 -916 -747 0 -508 -940 -229 -244 -761 0 -425 122 101 -813 -67 0 0 0 707 -272 -435 0 -736 228 586 826 -795 539 -553 -863 -744 -826 355 0 -6 -824 0 0 -588 -812 0 -109 -408 -153 -799 0 -15 -602 0 -874 -681 440 579 -577 0 -545 836 -810 -147 594 124 337 -477 -749 -313\\n\", \"100\\n-218 113 -746 -267 498 408 116 756 -793 0 -335 -213 593 -467 807 -342 -944 13 637 -82 -16 860 -333 -94 409 -149 -79 -431 -321 974 148 779 -860 -992 -598 0 -300 285 -187 404 -468 0 -586 875 0 0 -26 366 221 -759 -194 -353 -973 -968 -539 0 925 -223 -471 237 208 0 420 688 640 -711 964 661 708 -158 54 864 0 -697 -40 -313 -194 220 -211 108 596 534 148 -137 939 106 -730 -800 -266 433 421 -135 76 -51 -318 0 631 591 46 669\\n\", \"100\\n-261 613 -14 965 -114 -594 516 -631 -477 -352 -481 0 -224 -524 -841 397 -138 -986 -442 -568 -417 -850 -654 -193 -344 -648 -525 -394 -730 -712 -600 0 188 248 -657 -509 -647 -878 175 -894 -557 0 -367 -458 -35 -560 0 -952 -579 -784 -286 -303 -104 -984 0 0 487 -871 223 -527 0 -776 -675 -933 -669 -41 683 0 508 -443 807 -96 -454 -718 -806 -512 -990 -179 -909 0 421 -414 0 -290 0 -929 -675 611 -658 319 873 -421 876 -393 -289 -47 361 -693 -793 -33\\n\", \"50\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\\n\", \"50\\n-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1\\n\", \"50\\n9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9\\n\", \"50\\n-9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9\\n\", \"100\\n0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"100\\n-39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39\\n\", \"20\\n-918 -369 -810 -162 486 558 459 -792 -153 756 54 279 324 369 -783 828 -522 -333 -288 -612\\n\", \"50\\n-675 468 324 909 -621 918 954 846 369 -243 207 -756 225 -513 198 603 234 612 585 963 -396 801 -612 720 -432 -774 522 72 -747 -909 513 324 -27 846 -405 -252 -531 189 -36 -927 198 900 558 -711 702 -423 621 -945 -441 -783\\n\", \"100\\n216 -900 99 198 -945 -936 234 243 990 702 -657 225 -594 414 -36 990 720 -558 774 -927 -234 432 -342 180 522 -225 -936 -945 639 -702 -117 -63 720 747 144 -117 855 396 90 486 828 612 423 90 -423 -486 -729 45 -216 486 -108 -432 459 -351 -504 -639 -72 981 468 -81 -891 -999 297 126 -684 -27 477 -405 828 -72 -729 540 657 -270 -603 -9 864 -738 -954 -378 378 324 693 -225 -783 405 -999 -144 45 -207 999 -846 -63 -945 -135 981 54 360 -135 -261\\n\", \"100\\n-880 550 -605 -781 297 -748 209 385 429 748 -880 913 -924 -935 517 11 352 -99 -979 462 990 -495 -44 539 528 -22 -451 44 -781 451 792 275 -462 220 968 726 -88 385 55 77 341 715 275 -693 -880 616 440 -924 -451 -308 -770 -836 473 935 -660 957 418 -264 341 385 -55 -22 880 -539 539 -858 -121 165 -385 -198 99 -88 11 -231 -638 -440 814 -198 902 550 209 275 -319 -66 -176 -297 594 781 -33 -242 -385 -308 77 891 -781 0 -858 -22 825 -759\\n\", \"100\\n39 351 -39 663 -312 741 624 -39 -702 897 -234 -624 195 -897 -273 -624 39 -546 -858 390 390 -273 -741 156 -78 624 -117 390 -975 -234 390 897 936 -897 351 351 234 117 -663 -819 390 468 234 234 -78 -351 -897 702 -195 975 273 -429 624 -273 312 39 -117 -702 -507 195 -312 507 -858 -117 -117 858 468 858 546 702 -858 702 117 -702 663 -78 -702 -741 897 585 429 -741 897 546 195 975 -234 -936 78 -156 819 -897 507 -702 -858 975 -507 858 -390 -117\\n\", \"100\\n663 -408 -459 -255 204 -510 714 -561 -765 -510 765 -765 -357 -867 204 765 408 -153 255 459 306 -102 969 153 918 153 867 765 357 306 -663 918 408 357 714 561 0 459 255 204 867 -714 459 -51 102 -204 -816 -816 357 765 -459 -255 -357 153 408 510 -663 357 -714 408 867 -561 765 -153 969 663 612 51 867 -51 51 -663 204 153 969 663 -357 510 -714 714 -663 102 714 -255 -969 765 0 918 -612 -459 -204 0 306 102 663 -408 357 -510 -102 -510\\n\", \"100\\n-711 632 -395 79 -474 -237 -632 -632 316 -948 0 474 -79 -711 869 869 -948 -79 -316 474 237 -395 948 395 -158 -158 -632 237 -711 -632 -395 0 -316 474 -474 395 -474 79 0 -553 395 -948 -553 474 632 -237 -316 -711 553 948 790 237 -79 -553 -632 553 158 158 158 -79 948 -553 -474 632 395 79 -632 632 -869 -158 632 -553 -553 237 395 -237 711 -316 -948 -474 -632 316 869 869 948 -632 0 -237 -395 -474 79 553 -79 -158 553 711 474 632 711 0\\n\", \"100\\n0 1000 1000 1000 800 300 -500 900 400 -500 -900 400 400 -300 -300 -600 500 0 -500 600 -500 900 1000 -600 -200 300 -100 800 -800 0 200 400 0 -100 100 100 1000 -400 100 400 -900 -500 -900 400 -700 -400 800 -900 300 -300 -400 500 -900 1000 700 -200 500 400 -200 -300 -200 -600 -600 -800 300 -100 100 -1000 100 -800 -500 -800 0 100 900 -200 -100 -400 -500 0 -400 900 600 400 -200 100 400 800 -800 700 600 -200 1000 -400 -200 -200 100 -1000 700 -600\\n\", \"20\\n-828 -621 -36 -225 837 126 981 450 522 -522 -684 684 -477 792 -846 -405 639 495 27 -387\\n\", \"50\\n351 -729 -522 -936 -342 -189 -441 -279 -702 -369 864 873 -297 -261 -207 -54 -900 -675 -585 261 27 594 -360 702 -621 -774 729 846 864 -45 639 -216 -18 882 414 630 855 810 -135 783 -765 882 144 -477 -36 180 216 -180 -306 774\\n\", \"100\\n-270 -522 -855 -324 387 -297 126 -387 -927 414 882 945 -459 396 261 -243 234 -270 315 999 477 -315 -972 -396 -81 -207 522 9 477 -459 -18 -234 909 225 -18 396 351 297 -540 -981 648 -657 360 945 -486 -396 288 -567 9 882 -495 -585 729 -405 -864 468 -18 -279 315 -234 9 -963 -639 -540 783 279 -27 486 441 -522 -441 675 -495 -918 405 63 324 -81 -198 216 189 234 -414 -828 -675 144 -954 288 810 90 -918 63 -117 594 -846 972 873 72 504 -756\\n\", \"100\\n-473 517 517 154 -814 -836 649 198 803 -209 -363 759 -44 -242 -473 -715 561 451 -462 -110 -957 -792 462 132 -627 -473 363 572 -176 -935 -704 539 -286 22 374 286 451 748 -198 11 -616 319 264 -198 -638 -77 374 990 506 957 517 -297 -781 979 -121 539 -605 -264 946 869 616 -121 -792 -957 -22 528 715 869 506 -385 -869 121 -220 583 814 -814 33 -858 -121 308 825 55 -495 803 88 -187 -165 869 946 -594 -704 -209 11 770 -825 -44 -946 341 -330 -231\\n\", \"100\\n-900 -700 400 200 -800 500 1000 500 -300 -300 -100 900 -300 -300 900 -200 900 -800 -200 1000 -500 -200 -200 500 100 500 100 -400 -100 400 -500 700 400 -900 -300 -900 -700 1000 -800 1000 700 -200 -400 -900 -1000 400 300 800 -200 300 -500 -700 200 -200 -900 800 100 -700 -800 900 -900 -700 500 600 -700 300 -100 1000 100 -800 -200 -600 200 600 -100 -500 900 800 500 -600 900 600 600 -1000 800 -400 -800 900 500 -300 -300 400 1000 400 -1000 -200 -200 -100 -200 -800\\n\", \"20\\n0 0 0 -576 0 -207 0 -639 0 0 468 0 0 873 0 0 0 0 81 0\\n\", \"50\\n-81 -405 630 0 0 0 0 0 891 0 0 0 0 0 -18 0 0 0 0 0 243 -216 0 702 0 -909 -972 0 0 0 -450 0 0 882 0 0 0 0 0 -972 0 0 0 0 -333 -261 945 -720 0 -882\\n\", \"100\\n-972 0 -747 0 0 -918 396 0 0 -144 0 0 0 0 774 0 0 0 0 0 0 0 0 0 0 0 387 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 855 0 603 0 0 0 675 -675 621 0 0 0 -45 612 -549 -153 0 0 0 0 0 -486 0 0 0 0 0 0 -594 0 0 0 -225 0 -54 693 0 0 0 0 0 0 0 873 0 0 -198 0 0 0 0 558 0 918\\n\", \"100\\n0 0 0 0 0 0 0 0 539 0 0 -957 0 0 0 -220 0 550 0 0 0 660 0 0 -33 0 0 -935 0 0 0 0 0 0 0 0 0 0 0 0 0 -55 297 0 0 0 0 0 836 0 -451 0 0 0 0 0 -176 0 0 0 0 0 0 792 -847 330 0 0 0 715 0 0 0 517 -682 0 0 0 0 0 0 0 0 506 484 0 -396 0 0 429 0 0 0 0 0 0 0 968 0 0\\n\", \"100\\n0 0 0 0 0 0 0 0 0 0 0 600 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 900 100 0 0 0 1000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"100\\n49 0 -87 -39 0 0 -39 73 1 88 45 0 87 0 0 0 90 54 59 0 0 0 -96 -68 9 -26 0 68 21 59 -21 90 64 0 -62 78 -53 0 0 72 0 0 0 14 -79 87 0 75 0 97 77 0 37 0 1 18 0 0 0 30 47 39 0 -69 0 0 0 71 0 0 0 -85 0 44 0 0 0 -36 0 30 0 0 0 0 0 9 40 0 0 61 -35 0 0 0 0 -32 0 28 0 -100\\n\", \"100\\n-801 -258 -829 0 -839 -920 0 0 979 -896 -581 -132 -945 -274 -538 117 0 27 0 469 129 0 -608 685 0 -915 273 -929 0 -418 -57 517 -230 -775 0 -839 475 -350 882 363 419 0 -120 0 -416 808 0 -726 286 0 0 -777 -80 -331 0 278 -328 0 -534 0 0 -581 -463 0 -244 0 -693 0 0 -754 120 -254 -237 0 -452 0 -478 -509 0 -688 0 911 -219 368 0 0 -598 0 -575 0 0 -897 0 0 0 0 373 0 490 950\\n\", \"100\\n303 599 954 131 507 906 227 111 187 395 959 509 891 669 677 246 430 582 326 235 331 395 550 224 410 278 385 371 -829 514 600 451 337 786 508 939 548 23 583 342 870 585 16 914 482 619 781 583 683 913 663 727 329 170 475 557 356 8 342 536 821 348 942 486 497 732 213 659 351 -727 471 593 399 582 608 799 922 618 752 861 206 530 513 259 185 435 437 15 451 919 42 549 14 25 599 454 407 53 382 -540\\n\", \"100\\n-246 -98 -29 -208 -305 -231 -309 -632 -255 -293 -810 -283 -962 -593 -203 -40 -910 -934 -640 -520 -481 -988 -774 -696 -700 -875 -418 -750 -193 -863 -163 -498 -77 -627 -786 -820 -469 -799 -50 -162 -938 -133 -842 -144 -383 -245 -983 -975 -279 -86 -725 -304 -313 -574 -509 -192 -110 -726 -789 -36 -151 -792 -285 -988 -617 -738 -462 -921 -882 -299 -379 -640 -762 -363 -41 -942 -693 -92 -912 -187 -614 -509 -225 -649 -443 -867 -503 -596 -757 -711 -864 -378 -974 -141 -491 -98 -506 -113 -322 -558\\n\", \"100\\n34 -601 426 -318 -52 -51 0 782 711 0 502 746 -450 1 695 -606 951 942 14 0 -695 806 -195 -643 445 -903 443 523 -940 634 -229 -244 -303 -970 -564 -755 344 469 0 -293 306 496 786 62 0 -110 640 339 630 -276 -286 838 137 -508 811 -385 -784 -834 937 -361 -799 534 368 -352 -702 353 -437 -440 213 56 637 -814 -169 -56 930 720 -100 -696 -749 463 -32 761 -137 181 428 -408 0 727 -78 963 -606 -131 -537 827 951 -753 58 -21 -261 636\\n\", \"100\\n642 -529 -322 -893 -539 -300 -286 -503 -750 0 974 -560 -806 0 294 0 -964 -555 501 -308 -160 -369 -175 0 -257 -361 -976 -6 0 836 915 -353 -134 0 -511 -290 -854 87 190 790 -229 27 -67 -699 -200 -589 443 -534 -621 -265 0 -666 -497 999 -700 -149 -668 94 -623 -160 -385 -422 88 -818 -998 -665 -229 143 133 241 840 0 -764 873 -372 -741 262 -462 -481 -630 0 848 -875 65 302 -231 -514 -275 -874 -447 195 -393 350 678 -991 -904 -251 0 -376 -419\\n\", \"100\\n-48 842 18 424 -969 -357 -781 -517 -941 -957 -548 23 0 215 0 -649 -509 955 376 824 62 0 -5 674 890 263 -567 585 488 -862 66 961 75 205 838 756 514 -806 0 -884 692 0 301 -722 457 838 -649 -785 0 -775 449 -436 524 792 999 953 470 39 -61 0 860 65 420 382 0 11 0 117 767 171 0 577 185 385 387 -612 0 277 -738 -691 78 396 6 -766 155 119 -588 0 -724 228 580 200 -375 620 615 87 574 740 -398 698\\n\", \"10\\n1 1 1 1 1 -1 -1 -1 -1 -1\\n\", \"1\\n0\\n\", \"3\\n-1 0 1\\n\", \"3\\n0 0 -1\\n\", \"4\\n2 2 -2 -2\\n\", \"6\\n1 1 1 -1 -1 -1\\n\", \"7\\n1 2 3 0 0 -1 -1\\n\", \"5\\n0 1 2 -1 -2\\n\", \"2\\n-1 0\\n\", \"5\\n-1 -1 -1 -1 -1\\n\", \"5\\n100 0 0 0 0\\n\", \"4\\n1 1 -1 -1\\n\", \"4\\n1 0 -1 -1\\n\", \"1\\n-1\\n\", \"5\\n1 1 -1 -1 0\\n\", \"9\\n0 0 0 1 1 1 1 -1 -1\\n\", \"2\\n-1 1\\n\", \"4\\n0 0 -1 1\\n\", \"5\\n1 1 0 0 -1\\n\", \"4\\n1 -1 0 0\\n\", \"4\\n-1 -1 0 1\\n\", \"8\\n1 2 3 4 -1 -2 -3 -4\\n\", \"6\\n-1 -1 -1 0 0 0\\n\", \"3\\n-1 0 0\\n\", \"5\\n-1 -2 -3 0 80\\n\", \"8\\n-1 -1 1 0 0 0 0 0\\n\", \"5\\n0 0 1 1 -1\\n\", \"3\\n0 -1 1\\n\", \"3\\n1 0 -1\\n\", \"1\\n1000\\n\", \"9\\n2 2 2 2 -3 -3 -3 -3 0\\n\", \"4\\n-1 -1 0 0\\n\", \"7\\n-1 -1 -1 1 1 0 0\\n\", \"5\\n-1 -1 -1 0 0\\n\", \"5\\n-1 -2 -3 -4 -5\\n\", \"6\\n1 2 3 -1 -2 -3\\n\", \"4\\n-1 -2 0 2\\n\", \"5\\n-1 -1 0 0 0\\n\", \"4\\n0 0 -1 -1\\n\", \"6\\n0 0 1 1 -1 -1\\n\", \"3\\n-1 -1 0\\n\", \"6\\n-2 -1 0 0 0 0\\n\", \"9\\n1 1 1 0 0 0 -1 -1 -1\\n\", \"2\\n1 -1\\n\", \"8\\n-1 -1 -1 -1 0 0 1 1\\n\", \"6\\n1 1 0 0 -1 -1\\n\", \"5\\n1 1 0 -1 -1\\n\", \"9\\n1 2 3 -1 -2 -3 0 0 0\\n\", \"5\\n2 2 -2 -2 0\\n\", \"5\\n1 -1 0 0 0\\n\", \"6\\n1 1 -1 -1 0 0\\n\", \"4\\n0 1 0 -1\\n\", \"5\\n-2 -2 -2 1 1\\n\", \"7\\n1 1 1 0 -1 -1 -1\\n\", \"100\\n-261 613 -14 965 -114 -594 516 -631 -477 -352 -481 0 -224 -524 -841 397 -138 -986 -442 -568 -417 -850 -654 -193 -344 -648 -525 -394 -730 -712 -600 0 188 248 -657 -509 -647 -878 175 -894 -557 0 -367 -458 -35 -560 0 -952 -579 -784 -286 -303 -104 -984 0 0 487 -871 223 -527 0 -776 -675 -933 -669 -41 683 0 508 -443 807 -96 -454 -718 -806 -512 -990 -179 -909 0 421 -414 0 -290 0 -929 -675 611 -658 319 873 -421 876 -393 -289 -47 361 -693 -793 -33\\n\", \"100\\n642 -529 -322 -893 -539 -300 -286 -503 -750 0 974 -560 -806 0 294 0 -964 -555 501 -308 -160 -369 -175 0 -257 -361 -976 -6 0 836 915 -353 -134 0 -511 -290 -854 87 190 790 -229 27 -67 -699 -200 -589 443 -534 -621 -265 0 -666 -497 999 -700 -149 -668 94 -623 -160 -385 -422 88 -818 -998 -665 -229 143 133 241 840 0 -764 873 -372 -741 262 -462 -481 -630 0 848 -875 65 302 -231 -514 -275 -874 -447 195 -393 350 678 -991 -904 -251 0 -376 -419\\n\", \"10\\n-62 0 94 -49 84 -11 -88 0 -88 94\\n\", \"10\\n1 1 1 1 1 -1 -1 -1 -1 -1\\n\", \"8\\n-1 -1 -1 -1 0 0 1 1\\n\", \"5\\n100 0 0 0 0\\n\", \"100\\n-801 -258 -829 0 -839 -920 0 0 979 -896 -581 -132 -945 -274 -538 117 0 27 0 469 129 0 -608 685 0 -915 273 -929 0 -418 -57 517 -230 -775 0 -839 475 -350 882 363 419 0 -120 0 -416 808 0 -726 286 0 0 -777 -80 -331 0 278 -328 0 -534 0 0 -581 -463 0 -244 0 -693 0 0 -754 120 -254 -237 0 -452 0 -478 -509 0 -688 0 911 -219 368 0 0 -598 0 -575 0 0 -897 0 0 0 0 373 0 490 950\\n\", \"9\\n1 1 1 0 0 0 -1 -1 -1\\n\", \"50\\n-335 775 108 -928 -539 408 390 500 867 951 301 -113 -711 827 -83 422 -465 -355 -891 -957 -261 -507 930 385 745 198 238 33 805 -956 154 627 812 -518 216 785 817 -965 -916 999 986 718 55 698 -864 512 322 442 188 771\\n\", \"50\\n-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1\\n\", \"100\\n-473 517 517 154 -814 -836 649 198 803 -209 -363 759 -44 -242 -473 -715 561 451 -462 -110 -957 -792 462 132 -627 -473 363 572 -176 -935 -704 539 -286 22 374 286 451 748 -198 11 -616 319 264 -198 -638 -77 374 990 506 957 517 -297 -781 979 -121 539 -605 -264 946 869 616 -121 -792 -957 -22 528 715 869 506 -385 -869 121 -220 583 814 -814 33 -858 -121 308 825 55 -495 803 88 -187 -165 869 946 -594 -704 -209 11 770 -825 -44 -946 341 -330 -231\\n\", \"100\\n0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"3\\n1 0 -1\\n\", \"50\\n-306 -646 -572 -364 -706 796 900 -715 -808 -746 -49 -320 983 -414 -996 659 -439 -280 -913 126 -229 427 -493 -316 -831 -292 -942 707 -685 -82 654 490 -313 -660 -960 971 383 430 -145 -689 -757 -811 656 -419 244 203 -605 -287 44 -583\\n\", \"20\\n-918 -369 -810 -162 486 558 459 -792 -153 756 54 279 324 369 -783 828 -522 -333 -288 -612\\n\", \"100\\n39 351 -39 663 -312 741 624 -39 -702 897 -234 -624 195 -897 -273 -624 39 -546 -858 390 390 -273 -741 156 -78 624 -117 390 -975 -234 390 897 936 -897 351 351 234 117 -663 -819 390 468 234 234 -78 -351 -897 702 -195 975 273 -429 624 -273 312 39 -117 -702 -507 195 -312 507 -858 -117 -117 858 468 858 546 702 -858 702 117 -702 663 -78 -702 -741 897 585 429 -741 897 546 195 975 -234 -936 78 -156 819 -897 507 -702 -858 975 -507 858 -390 -117\\n\", \"2\\n1 -1\\n\", \"100\\n-246 -98 -29 -208 -305 -231 -309 -632 -255 -293 -810 -283 -962 -593 -203 -40 -910 -934 -640 -520 -481 -988 -774 -696 -700 -875 -418 -750 -193 -863 -163 -498 -77 -627 -786 -820 -469 -799 -50 -162 -938 -133 -842 -144 -383 -245 -983 -975 -279 -86 -725 -304 -313 -574 -509 -192 -110 -726 -789 -36 -151 -792 -285 -988 -617 -738 -462 -921 -882 -299 -379 -640 -762 -363 -41 -942 -693 -92 -912 -187 -614 -509 -225 -649 -443 -867 -503 -596 -757 -711 -864 -378 -974 -141 -491 -98 -506 -113 -322 -558\\n\", \"7\\n1 2 3 0 0 -1 -1\\n\", \"5\\n-1 -1 -1 0 0\\n\", \"20\\n74 33 43 41 -83 -30 0 -20 84 99 83 0 64 0 57 46 0 18 94 82\\n\", \"5\\n0 0 1 1 -1\\n\", \"5\\n0 0 0 1 1\\n\", \"5\\n1 1 -1 -1 0\\n\", \"6\\n-2 -1 0 0 0 0\\n\", \"100\\n216 -900 99 198 -945 -936 234 243 990 702 -657 225 -594 414 -36 990 720 -558 774 -927 -234 432 -342 180 522 -225 -936 -945 639 -702 -117 -63 720 747 144 -117 855 396 90 486 828 612 423 90 -423 -486 -729 45 -216 486 -108 -432 459 -351 -504 -639 -72 981 468 -81 -891 -999 297 126 -684 -27 477 -405 828 -72 -729 540 657 -270 -603 -9 864 -738 -954 -378 378 324 693 -225 -783 405 -999 -144 45 -207 999 -846 -63 -945 -135 981 54 360 -135 -261\\n\", \"100\\n49 0 -87 -39 0 0 -39 73 1 88 45 0 87 0 0 0 90 54 59 0 0 0 -96 -68 9 -26 0 68 21 59 -21 90 64 0 -62 78 -53 0 0 72 0 0 0 14 -79 87 0 75 0 97 77 0 37 0 1 18 0 0 0 30 47 39 0 -69 0 0 0 71 0 0 0 -85 0 44 0 0 0 -36 0 30 0 0 0 0 0 9 40 0 0 61 -35 0 0 0 0 -32 0 28 0 -100\\n\", \"4\\n2 2 -2 -2\\n\", \"100\\n-48 842 18 424 -969 -357 -781 -517 -941 -957 -548 23 0 215 0 -649 -509 955 376 824 62 0 -5 674 890 263 -567 585 488 -862 66 961 75 205 838 756 514 -806 0 -884 692 0 301 -722 457 838 -649 -785 0 -775 449 -436 524 792 999 953 470 39 -61 0 860 65 420 382 0 11 0 117 767 171 0 577 185 385 387 -612 0 277 -738 -691 78 396 6 -766 155 119 -588 0 -724 228 580 200 -375 620 615 87 574 740 -398 698\\n\", \"20\\n-828 -621 -36 -225 837 126 981 450 522 -522 -684 684 -477 792 -846 -405 639 495 27 -387\\n\", \"100\\n0 -927 -527 -306 -667 -229 -489 -194 -701 0 180 -723 0 3 -857 -918 -217 -471 732 -712 329 -40 0 0 -86 -820 -149 636 -260 -974 0 732 764 -769 916 -489 -916 -747 0 -508 -940 -229 -244 -761 0 -425 122 101 -813 -67 0 0 0 707 -272 -435 0 -736 228 586 826 -795 539 -553 -863 -744 -826 355 0 -6 -824 0 0 -588 -812 0 -109 -408 -153 -799 0 -15 -602 0 -874 -681 440 579 -577 0 -545 836 -810 -147 594 124 337 -477 -749 -313\\n\", \"5\\n-1 -2 -3 -4 -5\\n\", \"4\\n-1 -1 0 1\\n\", \"100\\n34 -601 426 -318 -52 -51 0 782 711 0 502 746 -450 1 695 -606 951 942 14 0 -695 806 -195 -643 445 -903 443 523 -940 634 -229 -244 -303 -970 -564 -755 344 469 0 -293 306 496 786 62 0 -110 640 339 630 -276 -286 838 137 -508 811 -385 -784 -834 937 -361 -799 534 368 -352 -702 353 -437 -440 213 56 637 -814 -169 -56 930 720 -100 -696 -749 463 -32 761 -137 181 428 -408 0 727 -78 963 -606 -131 -537 827 951 -753 58 -21 -261 636\\n\", \"6\\n1 1 0 0 -1 -1\\n\", \"3\\n-1 0 0\\n\", \"100\\n-322 -198 -448 -249 -935 614 67 -679 -616 430 -71 818 -595 -22 559 -575 -710 50 -542 -144 -977 672 -826 -927 457 518 603 -287 689 -45 -770 208 360 -498 -884 -161 -831 -793 -991 -102 -706 338 298 -897 236 567 -22 577 -77 -481 376 -152 861 559 190 -662 432 -880 -839 737 857 -614 -670 -423 -320 -451 -733 -304 822 -316 52 46 -438 -427 601 -885 -644 518 830 -517 719 643 216 45 -15 382 411 -424 -649 286 -265 -49 704 661 -2 -992 67 -118 299 -420\\n\", \"100\\n-218 113 -746 -267 498 408 116 756 -793 0 -335 -213 593 -467 807 -342 -944 13 637 -82 -16 860 -333 -94 409 -149 -79 -431 -321 974 148 779 -860 -992 -598 0 -300 285 -187 404 -468 0 -586 875 0 0 -26 366 221 -759 -194 -353 -973 -968 -539 0 925 -223 -471 237 208 0 420 688 640 -711 964 661 708 -158 54 864 0 -697 -40 -313 -194 220 -211 108 596 534 148 -137 939 106 -730 -800 -266 433 421 -135 76 -51 -318 0 631 591 46 669\\n\", \"20\\n-892 0 -413 742 0 0 754 23 -515 -293 0 918 -711 -362 -15 -776 -442 -902 116 732\\n\", \"4\\n-1 -2 0 2\\n\", \"100\\n0 0 0 0 0 0 0 0 539 0 0 -957 0 0 0 -220 0 550 0 0 0 660 0 0 -33 0 0 -935 0 0 0 0 0 0 0 0 0 0 0 0 0 -55 297 0 0 0 0 0 836 0 -451 0 0 0 0 0 -176 0 0 0 0 0 0 792 -847 330 0 0 0 715 0 0 0 517 -682 0 0 0 0 0 0 0 0 506 484 0 -396 0 0 429 0 0 0 0 0 0 0 968 0 0\\n\", \"100\\n0 0 0 0 0 0 0 0 0 0 0 600 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 900 100 0 0 0 1000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"4\\n1 -1 0 0\\n\", \"5\\n0 1 2 -1 -2\\n\", \"5\\n10 0 -7 2 6\\n\", \"5\\n1 1 0 -1 -1\\n\", \"5\\n2 2 -2 -2 0\\n\", \"4\\n0 0 -1 -1\\n\", \"6\\n0 0 1 1 -1 -1\\n\", \"100\\n-39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39\\n\", \"100\\n0 1000 1000 1000 800 300 -500 900 400 -500 -900 400 400 -300 -300 -600 500 0 -500 600 -500 900 1000 -600 -200 300 -100 800 -800 0 200 400 0 -100 100 100 1000 -400 100 400 -900 -500 -900 400 -700 -400 800 -900 300 -300 -400 500 -900 1000 700 -200 500 400 -200 -300 -200 -600 -600 -800 300 -100 100 -1000 100 -800 -500 -800 0 100 900 -200 -100 -400 -500 0 -400 900 600 400 -200 100 400 800 -800 700 600 -200 1000 -400 -200 -200 100 -1000 700 -600\\n\", \"4\\n1 0 -1 -1\\n\", \"50\\n-321 -535 -516 -822 -622 102 145 -607 338 -849 -499 892 -23 -120 40 -864 -452 -641 -902 41 745 -291 887 -175 -288 -69 -590 370 -421 195 904 558 886 89 -764 -378 276 -21 -531 668 872 88 -32 -558 230 181 -639 364 -940 177\\n\", \"100\\n-900 -700 400 200 -800 500 1000 500 -300 -300 -100 900 -300 -300 900 -200 900 -800 -200 1000 -500 -200 -200 500 100 500 100 -400 -100 400 -500 700 400 -900 -300 -900 -700 1000 -800 1000 700 -200 -400 -900 -1000 400 300 800 -200 300 -500 -700 200 -200 -900 800 100 -700 -800 900 -900 -700 500 600 -700 300 -100 1000 100 -800 -200 -600 200 600 -100 -500 900 800 500 -600 900 600 600 -1000 800 -400 -800 900 500 -300 -300 400 1000 400 -1000 -200 -200 -100 -200 -800\\n\", \"5\\n-1 -1 0 0 0\\n\", \"100\\n-880 550 -605 -781 297 -748 209 385 429 748 -880 913 -924 -935 517 11 352 -99 -979 462 990 -495 -44 539 528 -22 -451 44 -781 451 792 275 -462 220 968 726 -88 385 55 77 341 715 275 -693 -880 616 440 -924 -451 -308 -770 -836 473 935 -660 957 418 -264 341 385 -55 -22 880 -539 539 -858 -121 165 -385 -198 99 -88 11 -231 -638 -440 814 -198 902 550 209 275 -319 -66 -176 -297 594 781 -33 -242 -385 -308 77 891 -781 0 -858 -22 825 -759\\n\", \"50\\n9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9\\n\", \"3\\n-1 0 1\\n\", \"3\\n-1 -1 0\\n\", \"5\\n1 -1 0 0 0\\n\", \"50\\n351 -729 -522 -936 -342 -189 -441 -279 -702 -369 864 873 -297 -261 -207 -54 -900 -675 -585 261 27 594 -360 702 -621 -774 729 846 864 -45 639 -216 -18 882 414 630 855 810 -135 783 -765 882 144 -477 -36 180 216 -180 -306 774\\n\", \"3\\n0 -1 1\\n\", \"20\\n355 -184 -982 -685 581 139 249 -352 -856 -436 679 397 653 325 -639 -722 769 345 -207 -632\\n\", \"5\\n1 1 0 0 -1\\n\", \"50\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\\n\", \"9\\n0 0 0 1 1 1 1 -1 -1\\n\", \"5\\n-1 -2 -3 0 80\\n\", \"4\\n1 1 -1 -1\\n\", \"100\\n663 -408 -459 -255 204 -510 714 -561 -765 -510 765 -765 -357 -867 204 765 408 -153 255 459 306 -102 969 153 918 153 867 765 357 306 -663 918 408 357 714 561 0 459 255 204 867 -714 459 -51 102 -204 -816 -816 357 765 -459 -255 -357 153 408 510 -663 357 -714 408 867 -561 765 -153 969 663 612 51 867 -51 51 -663 204 153 969 663 -357 510 -714 714 -663 102 714 -255 -969 765 0 918 -612 -459 -204 0 306 102 663 -408 357 -510 -102 -510\\n\", \"100\\n621 862 494 -906 906 359 776 0 23 -868 863 -872 273 182 414 675 31 555 0 -423 468 517 577 892 117 664 292 11 105 589 173 455 711 358 229 -666 192 758 6 858 208 628 532 21 69 319 926 988 0 0 0 229 351 708 287 949 429 895 369 0 756 486 2 525 656 -906 742 284 174 510 747 227 274 103 50 -832 656 627 883 -603 927 989 797 463 615 798 832 535 562 517 194 697 661 176 814 -62 0 -886 239 221\\n\", \"50\\n40 -84 25 0 21 44 96 2 -49 -15 -58 58 0 -49 4 8 13 28 -78 69 0 35 43 0 41 97 99 0 0 5 71 58 10 15 0 30 49 0 -66 15 64 -51 0 50 0 23 43 -43 15 6\\n\", \"100\\n-270 -522 -855 -324 387 -297 126 -387 -927 414 882 945 -459 396 261 -243 234 -270 315 999 477 -315 -972 -396 -81 -207 522 9 477 -459 -18 -234 909 225 -18 396 351 297 -540 -981 648 -657 360 945 -486 -396 288 -567 9 882 -495 -585 729 -405 -864 468 -18 -279 315 -234 9 -963 -639 -540 783 279 -27 486 441 -522 -441 675 -495 -918 405 63 324 -81 -198 216 189 234 -414 -828 -675 144 -954 288 810 90 -918 63 -117 594 -846 972 873 72 504 -756\\n\", \"2\\n1 0\\n\", \"2\\n-1 1\\n\", \"100\\n303 599 954 131 507 906 227 111 187 395 959 509 891 669 677 246 430 582 326 235 331 395 550 224 410 278 385 371 -829 514 600 451 337 786 508 939 548 23 583 342 870 585 16 914 482 619 781 583 683 913 663 727 329 170 475 557 356 8 342 536 821 348 942 486 497 732 213 659 351 -727 471 593 399 582 608 799 922 618 752 861 206 530 513 259 185 435 437 15 451 919 42 549 14 25 599 454 407 53 382 -540\\n\", \"9\\n2 2 2 2 -3 -3 -3 -3 0\\n\", \"1\\n1000\\n\", \"9\\n1 2 3 -1 -2 -3 0 0 0\\n\", \"7\\n1 1 1 0 -1 -1 -1\\n\", \"7\\n-1 -1 -1 1 1 0 0\\n\", \"4\\n0 1 0 -1\\n\", \"50\\n-675 468 324 909 -621 918 954 846 369 -243 207 -756 225 -513 198 603 234 612 585 963 -396 801 -612 720 -432 -774 522 72 -747 -909 513 324 -27 846 -405 -252 -531 189 -36 -927 198 900 558 -711 702 -423 621 -945 -441 -783\\n\", \"1\\n0\\n\", \"50\\n-81 -405 630 0 0 0 0 0 891 0 0 0 0 0 -18 0 0 0 0 0 243 -216 0 702 0 -909 -972 0 0 0 -450 0 0 882 0 0 0 0 0 -972 0 0 0 0 -333 -261 945 -720 0 -882\\n\", \"50\\n-657 0 -595 -527 -354 718 919 -770 -775 943 -23 0 -428 -322 -68 -429 -784 -981 -294 -260 533 0 0 -96 -839 0 -981 187 248 -56 -557 0 510 -824 -850 -531 -92 386 0 -952 519 -417 811 0 -934 -495 -813 -810 -733 0\\n\", \"100\\n41 95 -57 5 -37 -58 61 0 59 42 45 64 35 84 11 53 5 -73 99 0 59 68 82 32 50 0 92 0 17 0 -2 82 86 -63 96 -7 0 0 -6 -86 96 88 81 82 0 41 9 0 67 88 80 84 78 0 16 66 0 17 56 46 82 0 11 -79 53 0 -94 73 12 93 30 75 89 0 56 90 79 -39 45 -18 38 52 82 8 -30 0 69 50 22 0 41 0 0 33 17 8 97 79 30 59\\n\", \"6\\n1 1 -1 -1 0 0\\n\", \"1\\n-1\\n\", \"100\\n39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39\\n\", \"1\\n777\\n\", \"6\\n-1 -1 -1 0 0 0\\n\", \"3\\n0 0 -1\\n\", \"100\\n-711 632 -395 79 -474 -237 -632 -632 316 -948 0 474 -79 -711 869 869 -948 -79 -316 474 237 -395 948 395 -158 -158 -632 237 -711 -632 -395 0 -316 474 -474 395 -474 79 0 -553 395 -948 -553 474 632 -237 -316 -711 553 948 790 237 -79 -553 -632 553 158 158 158 -79 948 -553 -474 632 395 79 -632 632 -869 -158 632 -553 -553 237 395 -237 711 -316 -948 -474 -632 316 869 869 948 -632 0 -237 -395 -474 79 553 -79 -158 553 711 474 632 711 0\\n\", \"100\\n-972 0 -747 0 0 -918 396 0 0 -144 0 0 0 0 774 0 0 0 0 0 0 0 0 0 0 0 387 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 855 0 603 0 0 0 675 -675 621 0 0 0 -45 612 -549 -153 0 0 0 0 0 -486 0 0 0 0 0 0 -594 0 0 0 -225 0 -54 693 0 0 0 0 0 0 0 873 0 0 -198 0 0 0 0 558 0 918\\n\", \"5\\n-1 -1 -1 -1 -1\\n\", \"6\\n1 1 1 -1 -1 -1\\n\", \"4\\n0 0 -1 1\\n\", \"8\\n1 2 3 4 -1 -2 -3 -4\\n\", \"8\\n-1 -1 1 0 0 0 0 0\\n\", \"50\\n-9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9 -9\\n\", \"4\\n-1 -1 0 0\\n\", \"6\\n1 2 3 -1 -2 -3\\n\", \"5\\n-2 -2 -2 1 1\\n\", \"2\\n-1 0\\n\", \"20\\n0 0 0 -576 0 -207 0 -639 0 0 468 0 0 873 0 0 0 0 81 0\\n\", \"100\\n-261 613 -14 965 -114 -594 516 -631 -477 -352 -481 0 -224 -524 -841 397 -138 -986 -442 -568 -417 -850 -654 -193 -344 -648 -525 -394 -730 -712 -600 0 188 248 -657 -509 -647 -878 175 -894 -557 0 -367 -458 -35 -560 0 -952 -579 -784 -286 -303 -104 -984 0 0 487 -871 223 -527 0 -776 -675 -933 -669 -41 683 0 508 -443 807 -96 -454 -718 -806 -512 -990 -179 -909 0 421 -414 0 -290 0 -929 -675 611 -658 319 873 -421 876 -159 -289 -47 361 -693 -793 -33\\n\", \"10\\n1 1 1 1 1 0 -1 -1 -1 -1\\n\", \"5\\n110 0 0 0 0\\n\", \"100\\n642 -529 -322 -893 -539 -300 -286 -503 -750 0 974 -560 -806 0 294 0 -964 -555 501 -308 -160 -369 -175 0 -257 -361 -976 -6 0 836 915 -353 -134 0 -511 -290 -854 87 190 790 -229 27 -67 -699 -200 -589 443 -534 -621 -265 0 -666 -497 999 -700 -149 -668 94 -623 -312 -385 -422 88 -818 -998 -665 -229 143 133 241 840 0 -764 873 -372 -741 262 -462 -481 -630 0 848 -875 65 302 -231 -514 -275 -874 -447 195 -393 350 678 -991 -904 -251 0 -376 -419\\n\", \"10\\n-62 0 186 -49 84 -11 -88 0 -88 94\\n\", \"8\\n-1 -1 -1 -1 -1 0 1 1\\n\", \"100\\n-801 -258 -829 0 -839 -920 0 0 979 -896 -581 -132 -945 -274 -538 117 0 27 0 469 129 0 -608 685 0 -915 273 -929 0 -418 -57 517 -230 -775 0 -839 475 -350 882 363 419 0 -120 0 -416 808 0 -726 286 0 0 -777 -80 -331 0 278 -328 0 -534 0 0 -581 -463 0 -244 0 -693 0 0 -754 120 -254 -237 0 -452 0 -478 -509 0 -688 0 911 -219 368 0 0 -598 0 -575 0 0 -897 0 0 1 0 373 0 490 950\\n\", \"9\\n1 1 1 -1 0 0 -1 -1 -1\\n\", \"50\\n-335 775 108 -928 -539 408 390 500 867 951 301 -113 -711 827 -83 422 -465 -355 -891 -957 -261 -507 930 385 745 198 238 33 805 -956 154 627 812 -518 216 785 817 -965 -916 999 986 718 55 698 -154 512 322 442 188 771\\n\", \"50\\n-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -2 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1\\n\", \"100\\n-473 517 517 154 -814 -836 649 198 803 -209 -363 1265 -44 -242 -473 -715 561 451 -462 -110 -957 -792 462 132 -627 -473 363 572 -176 -935 -704 539 -286 22 374 286 451 748 -198 11 -616 319 264 -198 -638 -77 374 990 506 957 517 -297 -781 979 -121 539 -605 -264 946 869 616 -121 -792 -957 -22 528 715 869 506 -385 -869 121 -220 583 814 -814 33 -858 -121 308 825 55 -495 803 88 -187 -165 869 946 -594 -704 -209 11 770 -825 -44 -946 341 -330 -231\\n\", \"100\\n0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1\\n\", \"3\\n1 -1 -1\\n\", \"50\\n-306 -646 -572 -364 -706 796 900 -715 -808 -746 -49 -320 983 -414 -996 659 -439 -280 -913 126 -229 427 -493 -316 -831 -292 -942 707 -685 -82 654 490 -313 -660 -960 971 383 430 -145 -689 -757 -811 656 -419 244 203 -343 -287 44 -583\\n\", \"20\\n-918 -369 -810 -162 486 558 459 -792 -153 756 80 279 324 369 -783 828 -522 -333 -288 -612\\n\", \"100\\n39 351 -39 663 -312 741 624 -39 -702 897 -234 -624 195 -897 -273 -624 39 -546 -858 390 390 -498 -741 156 -78 624 -117 390 -975 -234 390 897 936 -897 351 351 234 117 -663 -819 390 468 234 234 -78 -351 -897 702 -195 975 273 -429 624 -273 312 39 -117 -702 -507 195 -312 507 -858 -117 -117 858 468 858 546 702 -858 702 117 -702 663 -78 -702 -741 897 585 429 -741 897 546 195 975 -234 -936 78 -156 819 -897 507 -702 -858 975 -507 858 -390 -117\\n\", \"2\\n2 0\\n\", \"100\\n-246 -98 -29 -208 -305 -231 -309 -632 -255 -293 -810 -283 -962 -593 -203 -40 -910 -934 -640 -520 -481 -988 -774 -696 -700 -875 -418 -750 -193 -863 -163 -498 -77 -627 -786 -820 -469 -799 -50 -162 -938 -133 -842 -144 -383 -245 -983 -975 -279 -86 -725 -304 -313 -785 -509 -192 -110 -726 -789 -36 -151 -792 -285 -988 -617 -738 -462 -921 -882 -299 -379 -640 -762 -363 -41 -942 -693 -92 -912 -187 -614 -509 -225 -649 -443 -867 -503 -596 -757 -711 -864 -378 -974 -141 -491 -98 -506 -113 -322 -558\\n\", \"7\\n1 2 3 0 1 -1 -1\\n\", \"5\\n-1 -1 -1 0 1\\n\", \"20\\n74 33 43 41 -83 -30 0 -20 84 99 83 0 64 0 57 29 0 18 94 82\\n\", \"5\\n0 1 1 1 -1\\n\", \"5\\n0 0 0 1 2\\n\", \"5\\n1 1 -1 -2 0\\n\", \"6\\n-2 -1 0 1 0 0\\n\", \"100\\n216 -900 99 198 -945 -936 234 243 990 702 -657 225 -594 414 -36 990 720 -558 774 -927 -234 432 -342 180 522 -225 -936 -945 639 -702 -117 -63 720 747 144 -117 855 396 90 486 828 612 423 90 -423 -486 -729 45 -216 486 -108 -432 598 -351 -504 -639 -72 981 468 -81 -891 -999 297 126 -684 -27 477 -405 828 -72 -729 540 657 -270 -603 -9 864 -738 -954 -378 378 324 693 -225 -783 405 -999 -144 45 -207 999 -846 -63 -945 -135 981 54 360 -135 -261\\n\", \"100\\n49 0 -87 -39 0 0 -39 73 1 88 45 0 87 0 0 0 90 54 59 0 0 0 -96 -68 9 -26 0 68 21 59 -21 90 64 0 -62 78 -53 0 0 72 0 0 0 14 -79 87 0 75 0 97 77 0 37 0 1 18 0 0 0 30 47 39 1 -69 0 0 0 71 0 0 0 -85 0 44 0 0 0 -36 0 30 0 0 0 0 0 9 40 0 0 61 -35 0 0 0 0 -32 0 28 0 -100\\n\", \"4\\n2 4 -2 -2\\n\", \"100\\n-48 842 18 424 -969 -357 -781 -517 -941 -957 -548 23 0 215 0 -649 -509 955 376 824 62 0 -5 674 890 263 -567 585 488 -862 66 961 75 205 838 756 514 -806 0 -884 692 0 301 -722 457 838 -649 -785 0 -775 449 -436 524 792 999 953 470 39 -61 0 860 65 420 382 0 11 0 117 767 171 0 577 185 385 387 -612 1 277 -738 -691 78 396 6 -766 155 119 -588 0 -724 228 580 200 -375 620 615 87 574 740 -398 698\\n\", \"20\\n-828 -621 -36 -225 837 25 981 450 522 -522 -684 684 -477 792 -846 -405 639 495 27 -387\\n\", \"100\\n0 -927 -527 -306 -667 -229 -489 -194 -701 0 180 -723 0 3 -857 -918 -244 -471 732 -712 329 -40 0 0 -86 -820 -149 636 -260 -974 0 732 764 -769 916 -489 -916 -747 0 -508 -940 -229 -244 -761 0 -425 122 101 -813 -67 0 0 0 707 -272 -435 0 -736 228 586 826 -795 539 -553 -863 -744 -826 355 0 -6 -824 0 0 -588 -812 0 -109 -408 -153 -799 0 -15 -602 0 -874 -681 440 579 -577 0 -545 836 -810 -147 594 124 337 -477 -749 -313\\n\", \"5\\n0 -2 -3 -4 -5\\n\", \"4\\n-1 -1 0 2\\n\", \"100\\n34 -601 426 -318 -52 -51 0 782 711 0 502 746 -450 1 695 -606 951 942 14 0 -695 806 -195 -643 445 -903 443 523 -940 634 -229 -244 -303 -970 -564 -755 344 469 0 -293 306 496 786 62 0 -110 640 339 630 -276 -286 838 137 -508 811 -385 -784 -834 937 -361 -799 534 368 -352 -702 353 -437 -440 213 56 637 -814 -169 -56 930 720 -100 -696 -749 463 -32 761 -137 181 428 -408 0 727 -78 963 -606 -131 -537 827 240 -753 58 -21 -261 636\\n\", \"6\\n2 1 0 0 -1 -1\\n\", \"3\\n-1 1 1\\n\", \"100\\n-322 -198 -448 -249 -935 614 67 -679 -616 430 -71 818 -595 -22 559 -575 -710 50 -542 -144 -977 672 -826 -927 457 518 603 -287 689 -45 -770 208 360 -498 -884 -161 -831 -793 -991 -102 -706 338 298 -897 236 647 -22 577 -77 -481 376 -152 861 559 190 -662 432 -880 -839 737 857 -614 -670 -423 -320 -451 -733 -304 822 -316 52 46 -438 -427 601 -885 -644 518 830 -517 719 643 216 45 -15 382 411 -424 -649 286 -265 -49 704 661 -2 -992 67 -118 299 -420\\n\", \"100\\n-218 102 -746 -267 498 408 116 756 -793 0 -335 -213 593 -467 807 -342 -944 13 637 -82 -16 860 -333 -94 409 -149 -79 -431 -321 974 148 779 -860 -992 -598 0 -300 285 -187 404 -468 0 -586 875 0 0 -26 366 221 -759 -194 -353 -973 -968 -539 0 925 -223 -471 237 208 0 420 688 640 -711 964 661 708 -158 54 864 0 -697 -40 -313 -194 220 -211 108 596 534 148 -137 939 106 -730 -800 -266 433 421 -135 76 -51 -318 0 631 591 46 669\\n\", \"20\\n-892 0 -413 742 0 0 754 23 -515 -96 0 918 -711 -362 -15 -776 -442 -902 116 732\\n\", \"4\\n-1 -2 -1 2\\n\", \"100\\n0 0 0 0 0 0 0 0 539 0 -1 -957 0 0 0 -220 0 550 0 0 0 660 0 0 -33 0 0 -935 0 0 0 0 0 0 0 0 0 0 0 0 0 -55 297 0 0 0 0 0 836 0 -451 0 0 0 0 0 -176 0 0 0 0 0 0 792 -847 330 0 0 0 715 0 0 0 517 -682 0 0 0 0 0 0 0 0 506 484 0 -396 0 0 429 0 0 0 0 0 0 0 968 0 0\\n\", \"100\\n0 0 0 0 0 0 0 0 0 0 0 600 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 900 100 0 0 0 1000 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"4\\n1 -1 -1 0\\n\", \"5\\n0 1 4 -1 -2\\n\", \"5\\n9 0 -7 2 6\\n\", \"5\\n1 1 1 -1 -1\\n\", \"5\\n2 2 0 -2 0\\n\", \"4\\n0 0 -1 0\\n\", \"6\\n0 0 2 1 -1 -1\\n\", \"100\\n-39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -25 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39 -39\\n\", \"100\\n0 1000 1000 1000 800 300 -500 900 400 -500 -900 400 464 -300 -300 -600 500 0 -500 600 -500 900 1000 -600 -200 300 -100 800 -800 0 200 400 0 -100 100 100 1000 -400 100 400 -900 -500 -900 400 -700 -400 800 -900 300 -300 -400 500 -900 1000 700 -200 500 400 -200 -300 -200 -600 -600 -800 300 -100 100 -1000 100 -800 -500 -800 0 100 900 -200 -100 -400 -500 0 -400 900 600 400 -200 100 400 800 -800 700 600 -200 1000 -400 -200 -200 100 -1000 700 -600\\n\", \"4\\n1 0 0 -1\\n\", \"50\\n-321 -535 -516 -822 -622 102 145 -607 305 -849 -499 892 -23 -120 40 -864 -452 -641 -902 41 745 -291 887 -175 -288 -69 -590 370 -421 195 904 558 886 89 -764 -378 276 -21 -531 668 872 88 -32 -558 230 181 -639 364 -940 177\\n\", \"100\\n-900 -700 400 200 -800 500 1000 500 -300 -300 -100 900 -300 -300 900 -200 900 -800 -200 1000 -500 -200 -200 500 100 500 100 -400 -100 400 -500 700 400 -900 -300 -900 -700 1000 -800 1000 700 -200 -400 -900 -1000 400 300 800 -200 300 -500 -700 200 -200 -900 800 000 -700 -800 900 -900 -700 500 600 -700 300 -100 1000 100 -800 -200 -600 200 600 -100 -500 900 800 500 -600 900 600 600 -1000 800 -400 -800 900 500 -300 -300 400 1000 400 -1000 -200 -200 -100 -200 -800\\n\", \"5\\n-1 0 -1 0 1\\n\", \"100\\n-880 550 -605 -781 297 -748 209 385 429 748 -880 913 -924 -935 517 11 352 -99 -979 462 990 -495 -44 539 528 -22 -451 44 -781 451 792 275 -462 220 968 726 -88 385 55 77 341 715 275 -693 -880 616 440 -924 -451 -308 -770 -836 473 935 -660 957 418 -264 341 385 -55 -22 880 -539 539 -858 -121 165 -385 -198 99 -88 11 -231 -638 -440 814 -198 902 550 209 275 -319 -66 -176 -297 594 781 -33 -242 -385 -308 77 182 -781 0 -858 -22 825 -759\\n\", \"50\\n9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 10 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9\\n\", \"3\\n-1 0 2\\n\", \"3\\n-2 -1 0\\n\", \"5\\n1 -1 0 1 0\\n\", \"50\\n351 -729 -522 -936 -342 -189 -441 -279 -702 -369 864 873 -297 -261 -207 -54 -900 -675 -585 261 27 594 -360 702 -621 -774 729 846 864 -45 639 -216 -18 882 414 630 855 810 -135 783 -765 882 144 -209 -36 180 216 -180 -306 774\\n\", \"3\\n0 -2 1\\n\", \"20\\n355 -184 -982 -685 581 139 249 -352 -856 -436 679 397 653 325 -639 -741 769 345 -207 -632\\n\", \"5\\n1 1 0 1 -1\\n\", \"50\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1\\n\", \"9\\n0 0 0 1 1 1 1 0 -1\\n\", \"5\\n-2 -2 -3 0 80\\n\", \"4\\n1 1 -1 -2\\n\", \"100\\n663 -408 -459 -255 204 -510 714 -561 -765 -510 765 -765 -357 -867 204 765 408 -153 255 459 306 -102 969 153 918 153 867 765 357 306 -663 918 408 357 714 561 0 459 255 204 867 -714 459 -51 102 -204 -816 -816 357 765 -459 -255 -357 153 408 510 -663 357 -714 408 867 -561 765 -153 969 663 612 51 867 -51 51 -586 204 153 969 663 -357 510 -714 714 -663 102 714 -255 -969 765 0 918 -612 -459 -204 0 306 102 663 -408 357 -510 -102 -510\\n\", \"100\\n621 862 494 -906 906 359 776 0 23 -868 863 -872 273 182 414 675 33 555 0 -423 468 517 577 892 117 664 292 11 105 589 173 455 711 358 229 -666 192 758 6 858 208 628 532 21 69 319 926 988 0 0 0 229 351 708 287 949 429 895 369 0 756 486 2 525 656 -906 742 284 174 510 747 227 274 103 50 -832 656 627 883 -603 927 989 797 463 615 798 832 535 562 517 194 697 661 176 814 -62 0 -886 239 221\\n\", \"50\\n40 -84 25 0 21 44 96 2 -49 -15 -58 58 0 -49 4 8 13 28 -78 69 0 35 43 0 41 97 99 0 0 5 71 58 12 15 0 30 49 0 -66 15 64 -51 0 50 0 23 43 -43 15 6\\n\", \"100\\n-270 -522 -681 -324 387 -297 126 -387 -927 414 882 945 -459 396 261 -243 234 -270 315 999 477 -315 -972 -396 -81 -207 522 9 477 -459 -18 -234 909 225 -18 396 351 297 -540 -981 648 -657 360 945 -486 -396 288 -567 9 882 -495 -585 729 -405 -864 468 -18 -279 315 -234 9 -963 -639 -540 783 279 -27 486 441 -522 -441 675 -495 -918 405 63 324 -81 -198 216 189 234 -414 -828 -675 144 -954 288 810 90 -918 63 -117 594 -846 972 873 72 504 -756\\n\", \"2\\n2 -1\\n\", \"2\\n-2 1\\n\", \"100\\n303 599 954 131 507 906 227 111 187 395 959 509 891 669 677 246 430 582 326 235 331 395 550 224 410 278 385 371 -829 514 600 451 337 786 508 939 548 23 583 342 870 585 16 914 482 619 781 583 683 913 663 727 329 170 475 557 356 8 342 536 821 348 942 486 497 732 213 1157 351 -727 471 593 399 582 608 799 922 618 752 861 206 530 513 259 185 435 437 15 451 919 42 549 14 25 599 454 407 53 382 -540\\n\", \"9\\n2 2 2 2 -3 -6 -3 -3 0\\n\", \"1\\n1100\\n\", \"9\\n1 2 3 0 -2 -3 0 0 0\\n\", \"7\\n1 1 1 0 -2 -1 -1\\n\", \"7\\n-1 -1 -1 1 1 0 1\\n\", \"4\\n0 1 0 -2\\n\", \"50\\n-675 468 324 909 -621 918 954 846 369 -243 207 -756 225 -513 198 603 234 612 585 963 -396 801 -612 1142 -432 -774 522 72 -747 -909 513 324 -27 846 -405 -252 -531 189 -36 -927 198 900 558 -711 702 -423 621 -945 -441 -783\\n\", \"1\\n1\\n\", \"50\\n-81 -405 630 0 -1 0 0 0 891 0 0 0 0 0 -18 0 0 0 0 0 243 -216 0 702 0 -909 -972 0 0 0 -450 0 0 882 0 0 0 0 0 -972 0 0 0 0 -333 -261 945 -720 0 -882\\n\", \"50\\n-657 0 -595 -527 -354 718 919 -770 -775 943 -23 0 -428 -322 -68 -429 -784 -981 -294 -260 533 0 0 -96 -839 0 -981 187 248 -56 -982 0 510 -824 -850 -531 -92 386 0 -952 519 -417 811 0 -934 -495 -813 -810 -733 0\\n\", \"100\\n41 95 -57 5 -37 -58 61 0 59 42 45 64 35 84 11 53 5 -73 99 0 59 68 82 32 50 0 92 0 17 0 -2 82 86 -63 96 -7 0 0 -6 -86 96 88 81 82 -1 41 9 0 67 88 80 84 78 0 16 66 0 17 56 46 82 0 11 -79 53 0 -94 73 12 93 30 75 89 0 56 90 79 -39 45 -18 38 52 82 8 -30 0 69 50 22 0 41 0 0 33 17 8 97 79 30 59\\n\", \"6\\n1 1 -1 -1 1 0\\n\", \"1\\n-2\\n\", \"100\\n39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 53 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39 39\\n\", \"1\\n1224\\n\", \"6\\n-1 -2 -1 0 0 0\\n\", \"3\\n1 1 -1\\n\", \"100\\n-711 632 -395 79 -474 -237 -632 -632 316 -948 0 474 -79 -711 869 869 -948 -79 -316 474 237 -395 948 395 -158 -158 -632 237 -711 -632 -395 0 -316 474 -474 395 -474 79 0 -553 395 -948 -553 474 632 -237 -316 -711 553 948 790 237 -145 -553 -632 553 158 158 158 -79 948 -553 -474 632 395 79 -632 632 -869 -158 632 -553 -553 237 395 -237 711 -316 -948 -474 -632 316 869 869 948 -632 0 -237 -395 -474 79 553 -79 -158 553 711 474 632 711 0\\n\", \"100\\n-972 0 -747 0 0 -918 396 0 0 -144 0 0 0 0 774 0 0 0 0 0 0 0 0 0 0 0 387 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 855 0 603 0 0 0 675 -675 621 0 0 0 -45 612 -549 -153 0 0 0 0 0 -486 0 0 0 0 0 0 -594 0 0 0 -225 0 -54 693 0 0 0 0 0 0 0 873 0 0 -198 0 0 0 0 558 0 918\\n\", \"5\\n-1 -1 -1 -1 0\\n\", \"6\\n1 1 1 0 -1 -1\\n\", \"4\\n1 0 -1 1\\n\", \"8\\n1 2 3 4 -1 -2 -6 -4\\n\", \"7\\n0 0 1 -1 0 0 2\\n\", \"5\\n10 0 -7 2 6\"], \"outputs\": [\"1\", \"0\", \"0\", \"1\", \"1\", \"1\", \"-1\", \"1\", \"-1\", \"1\", \"-1\", \"1\", \"1\", \"-1\", \"-1\", \"1\", \"-1\", \"1\", \"-1\", \"0\", \"-1\", \"1\", \"-1\", \"1\", \"-1\", \"0\", \"-1\", \"-1\", \"1\", \"-1\", \"1\", \"1\", \"1\", \"-1\", \"0\", \"1\", \"-1\", \"1\", \"1\", \"-1\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"1\", \"-1\", \"0\", \"-1\", \"1\", \"1\", \"0\", \"0\", \"0\", \"1\", \"1\", \"0\", \"0\", \"-1\", \"-1\", \"0\", \"1\", \"-1\", \"-1\", \"0\", \"0\", \"1\", \"0\", \"0\", \"0\", \"-1\", \"1\", \"-1\", \"0\", \"-1\", \"0\", \"0\", \"0\", \"0\", \"1\", \"0\", \"-1\", \"0\", \"-1\", \"-1\", \"1\", \"-1\", \"0\", \"-1\", \"0\", \"-1\", \"0\", \"0\", \"1\", \"-1\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"-1\", \"0\", \"-1\", \"-1\", \"-1\", \"1\", \"-1\", \"0\", \"0\", \"0\", \"1\", \"-1\", \"1\", \"0\", \"0\", \"-1\", \"-1\", \"1\", \"1\", \"-1\", \"0\", \"-1\", \"1\", \"0\", \"0\", \"0\", \"0\", \"-1\", \"0\", \"1\", \"1\", \"1\", \"-1\", \"-1\", \"-1\", \"0\", \"0\", \"0\", \"-1\", \"0\", \"-1\", \"-1\", \"0\", \"0\", \"0\", \"0\", \"1\", \"0\", \"0\", \"-1\", \"0\", \"-1\", \"0\", \"-1\", \"-1\", \"-1\", \"0\", \"1\", \"1\", \"0\", \"-1\", \"0\", \"-1\", \"0\", \"1\", \"0\", \"1\", \"0\", \"-1\", \"1\", \"1\", \"1\", \"1\", \"1\", \"1\", \"1\", \"1\", \"0\", \"1\", \"0\", \"0\", \"0\", \"0\", \"1\", \"0\", \"0\", \"-1\", \"1\", \"0\", \"-1\", \"1\", \"1\", \"-1\", \"0\", \"-1\", \"0\", \"-1\", \"1\", \"0\", \"1\", \"0\", \"-1\", \"-1\", \"1\", \"-1\", \"-1\", \"0\\n\", \"-1\\n\", \"1\\n\", \"0\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"0\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"-1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"-1\\n\", \"0\\n\", \"-1\\n\", \"-1\\n\", \"0\\n\", \"0\\n\", \"-1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"-1\\n\", \"0\\n\", \"0\\n\", \"-1\\n\", \"-1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"-1\\n\", \"0\\n\", \"-1\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"1\\n\", \"0\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"-1\\n\", \"1\\n\", \"-1\\n\", \"0\\n\", \"-1\\n\", \"1\\n\", \"1\\n\", \"1\\n\", \"0\", \"1\"]}", "source": "taco"}
|
You are given an array of $n$ integers: $a_1, a_2, \ldots, a_n$. Your task is to find some non-zero integer $d$ ($-10^3 \leq d \leq 10^3$) such that, after each number in the array is divided by $d$, the number of positive numbers that are presented in the array is greater than or equal to half of the array size (i.e., at least $\lceil\frac{n}{2}\rceil$). Note that those positive numbers do not need to be an integer (e.g., a $2.5$ counts as a positive number). If there are multiple values of $d$ that satisfy the condition, you may print any of them. In case that there is no such $d$, print a single integer $0$.
Recall that $\lceil x \rceil$ represents the smallest integer that is not less than $x$ and that zero ($0$) is neither positive nor negative.
-----Input-----
The first line contains one integer $n$ ($1 \le n \le 100$) — the number of elements in the array.
The second line contains $n$ space-separated integers $a_1, a_2, \ldots, a_n$ ($-10^3 \le a_i \le 10^3$).
-----Output-----
Print one integer $d$ ($-10^3 \leq d \leq 10^3$ and $d \neq 0$) that satisfies the given condition. If there are multiple values of $d$ that satisfy the condition, you may print any of them. In case that there is no such $d$, print a single integer $0$.
-----Examples-----
Input
5
10 0 -7 2 6
Output
4
Input
7
0 0 1 -1 0 0 2
Output
0
-----Note-----
In the first sample, $n = 5$, so we need at least $\lceil\frac{5}{2}\rceil = 3$ positive numbers after division. If $d = 4$, the array after division is $[2.5, 0, -1.75, 0.5, 1.5]$, in which there are $3$ positive numbers (namely: $2.5$, $0.5$, and $1.5$).
In the second sample, there is no valid $d$, so $0$ should be printed.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3 4 5\\n10 30 15\\n12 31 14 18\\n0 1 2 3 4\\n\", \"1 1 1\\n1\\n1\\n1\\n\", \"1 1 1\\n1\\n1\\n1\\n\", \"3 4 5\\n10 30 15\\n12 31 14 7\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 31 14 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 31 27 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 31 17 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 58 14 18\\n0 1 2 3 4\\n\", \"3 4 5\\n10 57 15\\n12 31 14 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 31 13 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 30\\n12 31 17 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 22 14 4\\n0 1 2 3 4\\n\", \"3 4 5\\n10 57 15\\n12 31 14 7\\n0 2 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 76 14 18\\n0 2 2 3 4\\n\", \"3 4 5\\n10 30 30\\n12 57 17 6\\n0 1 2 1 4\\n\", \"3 4 5\\n20 30 15\\n12 76 14 18\\n0 2 2 3 4\\n\", \"3 4 5\\n10 30 30\\n12 57 17 6\\n0 2 2 1 4\\n\", \"3 4 5\\n10 30 30\\n12 57 17 6\\n0 2 2 1 1\\n\", \"3 4 5\\n10 30 15\\n12 31 14 18\\n0 1 1 3 4\\n\", \"3 4 5\\n10 30 3\\n12 31 14 7\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 26\\n12 31 14 7\\n0 1 2 4 4\\n\", \"3 4 5\\n10 30 15\\n12 31 14 7\\n0 1 0 1 4\\n\", \"3 4 5\\n10 30 15\\n12 56 27 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 58 20 18\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 31 14 4\\n0 1 2 0 4\\n\", \"3 4 5\\n10 30 15\\n15 31 13 7\\n0 1 2 1 4\\n\", \"3 4 5\\n8 30 15\\n12 76 14 18\\n0 2 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 22 28 4\\n0 1 2 3 4\\n\", \"3 4 5\\n1 30 15\\n12 45 14 7\\n0 1 2 4 7\\n\", \"3 4 5\\n10 30 30\\n12 57 17 6\\n0 1 2 1 6\\n\", \"3 4 5\\n20 30 28\\n12 76 14 18\\n0 2 2 3 4\\n\", \"3 4 5\\n7 30 30\\n12 57 17 6\\n0 2 2 1 4\\n\", \"3 4 5\\n20 9 15\\n12 76 14 18\\n0 2 2 3 4\\n\", \"3 4 5\\n10 60 30\\n12 57 17 6\\n0 2 2 1 1\\n\", \"3 4 5\\n10 6 30\\n12 57 26 6\\n0 2 2 1 1\\n\", \"3 4 5\\n10 18 15\\n12 31 14 18\\n0 1 1 3 4\\n\", \"3 4 5\\n11 30 26\\n12 31 14 7\\n0 1 2 4 4\\n\", \"3 4 5\\n10 30 15\\n22 56 27 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 58 20 18\\n0 1 1 3 4\\n\", \"3 4 5\\n10 30 15\\n12 31 20 4\\n0 1 2 0 4\\n\", \"3 4 5\\n10 45 15\\n12 31 14 13\\n0 2 2 1 4\\n\", \"3 4 5\\n10 31 30\\n12 57 17 6\\n0 1 2 1 6\\n\", \"3 4 5\\n10 4 30\\n12 57 26 6\\n0 2 2 1 1\\n\", \"3 4 5\\n10 18 15\\n12 31 14 0\\n0 1 1 3 4\\n\", \"3 4 5\\n10 30 3\\n12 31 12 7\\n0 1 3 3 4\\n\", \"3 4 5\\n10 30 15\\n12 58 7 18\\n0 1 1 3 4\\n\", \"3 4 5\\n10 30 20\\n12 31 20 4\\n0 1 2 0 4\\n\", \"3 4 5\\n10 45 15\\n5 31 14 13\\n0 2 2 1 4\\n\", \"3 4 5\\n10 37 30\\n12 57 17 6\\n0 1 2 1 6\\n\", \"3 4 5\\n10 4 30\\n12 57 26 6\\n0 2 2 1 2\\n\", \"3 4 5\\n10 18 15\\n22 31 14 0\\n0 1 1 3 4\\n\", \"3 4 5\\n5 30 3\\n12 31 12 7\\n0 1 3 3 4\\n\", \"3 4 5\\n10 43 20\\n12 31 20 4\\n0 1 2 0 4\\n\", \"3 4 5\\n10 45 15\\n5 31 16 13\\n0 2 2 1 4\\n\", \"3 4 5\\n10 36 30\\n12 57 47 6\\n0 2 2 1 1\\n\", \"3 4 5\\n5 32 3\\n12 31 12 7\\n0 1 3 3 4\\n\", \"3 4 5\\n8 43 20\\n12 31 20 4\\n0 1 2 0 4\\n\", \"3 4 5\\n20 5 28\\n12 76 14 18\\n1 0 3 3 4\\n\", \"3 4 5\\n10 36 30\\n19 57 47 6\\n0 2 2 1 1\\n\", \"3 4 5\\n5 32 3\\n12 31 12 7\\n0 1 3 3 8\\n\", \"3 4 5\\n9 43 20\\n12 31 20 4\\n0 1 2 0 4\\n\", \"3 4 5\\n3 45 15\\n5 31 16 13\\n0 2 2 1 6\\n\", \"3 4 5\\n10 10 15\\n22 31 14 0\\n1 2 1 3 4\\n\", \"3 4 5\\n5 32 3\\n19 31 12 7\\n0 1 3 3 8\\n\", \"3 4 5\\n3 45 13\\n5 31 16 13\\n0 2 2 1 6\\n\", \"3 4 5\\n0 5 28\\n12 76 14 18\\n0 0 3 3 4\\n\", \"3 4 5\\n5 32 3\\n19 31 12 7\\n0 1 3 3 15\\n\", \"3 4 5\\n9 43 20\\n3 31 20 6\\n0 1 2 0 4\\n\", \"3 4 5\\n3 45 13\\n5 24 27 13\\n0 2 2 1 6\\n\", \"3 4 5\\n9 43 10\\n3 31 20 6\\n1 1 2 0 4\\n\", \"3 4 5\\n3 45 18\\n5 24 27 13\\n0 2 2 1 6\\n\", \"3 4 5\\n3 41 18\\n5 24 27 13\\n0 2 2 1 6\\n\", \"3 4 5\\n3 41 21\\n5 24 27 13\\n0 2 2 1 6\\n\", \"3 4 5\\n3 24 21\\n5 24 27 13\\n0 2 2 1 6\\n\", \"3 4 5\\n3 24 17\\n5 24 27 13\\n0 2 2 1 6\\n\", \"3 4 5\\n10 30 10\\n12 31 14 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 31 17 7\\n0 0 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 58 14 18\\n0 1 2 0 4\\n\", \"3 4 5\\n10 30 5\\n12 31 13 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 30\\n12 31 17 13\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n13 22 14 4\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 45 14 7\\n0 2 2 4 7\\n\", \"3 4 5\\n10 57 15\\n12 31 24 7\\n0 2 2 1 4\\n\", \"3 4 5\\n10 30 30\\n12 31 17 6\\n0 2 2 1 4\\n\", \"3 4 5\\n10 30 15\\n1 22 14 6\\n0 1 2 3 4\\n\", \"3 4 5\\n10 52 30\\n12 57 17 6\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 17 14 6\\n1 1 2 3 4\\n\", \"3 4 5\\n10 30 30\\n12 57 26 6\\n0 2 0 1 1\\n\", \"3 4 5\\n10 30 3\\n12 31 14 7\\n0 1 2 4 4\\n\", \"3 4 5\\n10 46 26\\n12 31 14 7\\n0 1 2 4 4\\n\", \"3 4 5\\n10 30 15\\n12 31 19 7\\n0 1 0 1 4\\n\", \"3 4 5\\n10 30 27\\n12 22 14 5\\n0 1 2 3 4\\n\", \"3 4 5\\n20 30 18\\n12 76 14 18\\n0 2 2 3 4\\n\", \"3 4 5\\n7 30 11\\n12 57 17 6\\n0 2 2 1 4\\n\", \"3 4 5\\n10 60 30\\n12 57 17 6\\n0 2 1 1 1\\n\", \"3 4 5\\n20 18 15\\n12 31 14 18\\n0 1 1 3 4\\n\", \"3 4 5\\n3 30 15\\n22 56 27 7\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 58 20 18\\n0 1 1 2 4\\n\", \"3 4 5\\n10 54 15\\n12 31 20 4\\n0 1 2 0 4\\n\", \"3 4 5\\n7 55 30\\n22 57 17 6\\n0 2 2 1 4\\n\", \"3 4 5\\n10 4 30\\n12 57 26 7\\n0 2 2 1 1\\n\", \"3 4 5\\n10 34 15\\n12 31 14 0\\n0 1 1 3 4\\n\", \"3 4 5\\n10 30 3\\n12 31 12 7\\n1 1 3 3 4\\n\", \"3 4 5\\n10 45 15\\n5 31 14 13\\n0 3 2 1 4\\n\", \"3 4 5\\n20 30 14\\n12 76 14 18\\n1 0 2 3 4\\n\", \"3 4 5\\n10 18 15\\n22 13 14 0\\n0 1 1 3 4\\n\", \"3 4 5\\n5 30 1\\n12 31 12 7\\n0 1 3 3 4\\n\", \"3 4 5\\n10 43 40\\n12 31 20 4\\n0 1 2 0 4\\n\", \"3 4 5\\n10 45 15\\n5 31 16 21\\n0 2 2 1 4\\n\", \"3 4 5\\n38 30 28\\n12 76 14 18\\n1 0 3 3 4\\n\", \"3 4 5\\n10 36 16\\n12 57 47 6\\n0 2 2 1 1\\n\", \"3 4 5\\n10 18 12\\n22 31 14 0\\n1 1 1 3 4\\n\", \"3 4 5\\n8 43 4\\n12 31 20 4\\n0 1 2 0 4\\n\", \"3 4 5\\n10 36 30\\n31 57 47 6\\n0 2 2 1 1\\n\", \"3 4 5\\n3 45 15\\n5 31 16 13\\n1 2 2 1 6\\n\", \"3 4 5\\n10 10 4\\n22 31 14 0\\n1 2 1 3 4\\n\", \"3 4 5\\n9 43 20\\n12 31 20 11\\n0 1 2 0 4\\n\", \"3 4 5\\n10 36 60\\n19 57 23 0\\n0 2 2 1 1\\n\", \"3 4 5\\n5 32 4\\n19 31 12 7\\n0 1 3 3 15\\n\", \"3 4 5\\n7 43 10\\n3 31 20 6\\n1 1 2 0 4\\n\", \"3 4 5\\n3 45 13\\n5 24 27 13\\n0 2 1 1 6\\n\", \"3 4 5\\n3 41 21\\n5 24 27 13\\n0 2 2 1 11\\n\", \"3 4 5\\n3 24 24\\n5 24 27 1\\n0 2 2 1 6\\n\", \"3 4 5\\n3 24 17\\n5 24 5 2\\n0 2 2 1 6\\n\", \"3 4 5\\n3 24 17\\n5 37 27 2\\n0 2 2 2 6\\n\", \"3 4 5\\n5 30 10\\n12 31 14 7\\n0 1 2 1 4\\n\", \"3 4 5\\n13 30 15\\n12 31 17 7\\n0 0 2 1 4\\n\", \"3 4 5\\n10 30 15\\n11 58 14 18\\n0 1 2 0 4\\n\", \"3 4 5\\n16 30 5\\n12 31 13 7\\n0 1 2 1 4\\n\", \"3 4 5\\n14 30 15\\n13 22 14 4\\n0 1 2 3 4\\n\", \"3 4 5\\n10 68 15\\n12 31 24 7\\n0 2 2 1 4\\n\", \"3 4 5\\n13 30 15\\n1 22 14 6\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 17 14 6\\n1 1 0 3 4\\n\", \"3 4 5\\n10 44 15\\n12 76 14 18\\n0 2 2 3 5\\n\", \"3 4 5\\n10 30 15\\n12 31 14 7\\n0 1 2 4 4\\n\", \"3 4 5\\n10 30 15\\n12 31 14 4\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 31 14 7\\n0 1 2 4 7\\n\", \"3 4 5\\n10 30 15\\n12 76 14 18\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 45 14 7\\n0 1 2 4 7\\n\", \"3 4 5\\n10 30 30\\n12 31 17 6\\n0 1 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 22 14 6\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 22 14 6\\n1 1 2 3 4\\n\", \"3 4 5\\n20 30 15\\n12 76 14 18\\n0 2 2 3 5\\n\", \"3 4 5\\n10 30 30\\n12 57 26 6\\n0 2 2 1 1\\n\", \"3 4 5\\n10 57 15\\n12 31 14 13\\n0 2 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 22 14 5\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 3\\n12 31 14 7\\n0 1 3 3 4\\n\", \"3 4 5\\n10 30 15\\n15 31 13 7\\n0 1 2 2 4\\n\", \"3 4 5\\n10 30 15\\n12 22 5 4\\n0 1 2 3 4\\n\", \"3 4 5\\n20 30 28\\n12 76 14 18\\n1 2 2 3 4\\n\", \"3 4 5\\n7 30 30\\n22 57 17 6\\n0 2 2 1 4\\n\", \"3 4 5\\n10 60 30\\n12 57 28 6\\n0 2 2 1 1\\n\", \"3 4 5\\n10 30 15\\n22 56 27 7\\n0 1 2 0 4\\n\", \"3 4 5\\n20 30 28\\n12 76 14 18\\n1 0 2 3 4\\n\", \"3 4 5\\n10 60 30\\n12 57 47 6\\n0 2 2 1 1\\n\", \"3 4 5\\n10 30 15\\n22 56 27 7\\n0 1 2 0 5\\n\", \"3 4 5\\n20 30 28\\n12 76 14 18\\n1 0 3 3 4\\n\", \"3 4 5\\n10 18 15\\n22 31 14 0\\n1 1 1 3 4\\n\", \"3 4 5\\n10 30 15\\n22 56 27 7\\n0 1 2 1 5\\n\", \"3 4 5\\n10 45 15\\n5 31 16 13\\n0 2 2 1 6\\n\", \"3 4 5\\n10 18 15\\n22 31 14 0\\n1 2 1 3 4\\n\", \"3 4 5\\n20 5 28\\n12 76 14 18\\n0 0 3 3 4\\n\", \"3 4 5\\n10 36 30\\n19 57 23 6\\n0 2 2 1 1\\n\", \"3 4 5\\n9 43 20\\n12 31 20 6\\n0 1 2 0 4\\n\", \"3 4 5\\n10 36 30\\n19 57 23 0\\n0 2 2 1 1\\n\", \"3 4 5\\n3 45 13\\n5 24 16 13\\n0 2 2 1 6\\n\", \"3 4 5\\n9 43 20\\n3 31 20 6\\n1 1 2 0 4\\n\", \"3 4 5\\n3 24 17\\n5 24 27 1\\n0 2 2 1 6\\n\", \"3 4 5\\n3 24 17\\n5 24 27 2\\n0 2 2 1 6\\n\", \"3 4 5\\n3 24 17\\n5 37 27 2\\n0 2 2 1 6\\n\", \"3 4 5\\n10 30 15\\n12 37 14 7\\n0 1 2 4 4\\n\", \"3 4 5\\n10 30 15\\n12 31 14 7\\n0 1 2 4 13\\n\", \"3 4 5\\n10 30 15\\n12 76 14 18\\n0 2 2 3 8\\n\", \"3 4 5\\n10 30 30\\n12 57 3 6\\n0 2 2 1 4\\n\", \"3 4 5\\n10 30 15\\n12 76 14 18\\n0 2 2 3 5\\n\", \"3 4 5\\n10 30 15\\n12 114 20 18\\n0 1 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 31 9 4\\n0 1 2 0 4\\n\", \"3 4 5\\n8 30 15\\n12 108 14 18\\n0 2 2 3 4\\n\", \"3 4 5\\n10 30 15\\n12 12 28 4\\n0 1 2 3 4\\n\", \"3 4 5\\n10 57 15\\n12 48 14 13\\n0 2 2 1 4\\n\", \"3 4 5\\n20 9 15\\n12 76 14 18\\n0 1 2 3 4\\n\", \"3 4 5\\n10 6 30\\n12 57 23 6\\n0 2 2 1 1\\n\", \"3 4 5\\n11 30 26\\n12 31 14 3\\n0 1 2 4 4\\n\", \"3 4 5\\n10 30 15\\n15 31 13 7\\n0 1 2 2 5\\n\", \"3 4 5\\n20 30 28\\n12 76 14 18\\n1 2 2 3 8\\n\", \"3 4 5\\n10 60 30\\n12 57 28 6\\n1 2 2 1 1\\n\", \"3 4 5\\n10 30 15\\n22 56 27 7\\n0 1 3 0 4\\n\", \"3 4 5\\n10 30 15\\n12 58 7 18\\n0 1 1 5 4\\n\", \"3 4 5\\n10 30 20\\n12 31 19 4\\n0 1 2 0 4\\n\", \"3 4 5\\n10 37 30\\n12 57 17 6\\n1 1 2 1 6\\n\", \"3 4 5\\n10 60 30\\n12 57 47 6\\n0 2 2 1 0\\n\", \"3 4 5\\n10 30 15\\n22 56 2 7\\n0 1 2 1 5\\n\", \"3 4 5\\n10 45 15\\n5 31 16 13\\n0 2 2 2 6\\n\", \"3 4 5\\n20 5 28\\n12 76 14 18\\n2 0 3 3 4\\n\", \"3 4 5\\n5 32 3\\n12 31 12 7\\n1 1 3 3 8\\n\", \"3 4 5\\n20 5 28\\n12 89 14 18\\n0 0 3 3 4\\n\", \"3 4 5\\n10 36 30\\n19 57 32 6\\n0 2 2 1 1\\n\", \"3 4 5\\n0 5 28\\n12 76 14 18\\n0 0 3 6 4\\n\", \"3 4 5\\n9 43 10\\n3 31 20 6\\n0 1 2 0 4\\n\", \"3 4 5\\n3 45 13\\n5 24 16 13\\n0 2 2 0 6\\n\", \"3 4 5\\n9 43 20\\n3 31 31 6\\n1 1 2 0 4\\n\", \"3 4 5\\n3 24 17\\n5 24 27 13\\n1 2 2 1 6\\n\", \"3 4 5\\n10 30 15\\n21 37 14 7\\n0 1 2 4 4\\n\", \"3 4 5\\n10 30 15\\n12 31 14 18\\n0 1 2 3 4\\n\"], \"outputs\": [\"55\\n56\\n60\\n64\\n64\\n\", \"1\\n\", \"1\\n\", \"55\\n56\\n60\\n60\\n60\\n\", \"55\\n56\\n60\\n56\\n60\\n\", \"55\\n56\\n58\\n56\\n58\\n\", \"55\\n56\\n60\\n56\\n63\\n\", \"55\\n55\\n59\\n63\\n63\\n\", \"82\\n82\\n86\\n82\\n86\\n\", \"55\\n56\\n59\\n56\\n59\\n\", \"70\\n71\\n73\\n71\\n73\\n\", \"55\\n55\\n59\\n59\\n59\\n\", \"82\\n86\\n86\\n82\\n86\\n\", \"55\\n59\\n59\\n63\\n63\\n\", \"70\\n70\\n72\\n70\\n72\\n\", \"65\\n65\\n65\\n68\\n68\\n\", \"70\\n72\\n72\\n70\\n72\\n\", \"70\\n72\\n72\\n70\\n70\\n\", \"55\\n56\\n56\\n64\\n64\\n\", \"43\\n44\\n48\\n48\\n57\\n\", \"66\\n67\\n71\\n75\\n75\\n\", \"55\\n56\\n55\\n56\\n60\\n\", \"55\\n55\\n57\\n55\\n57\\n\", \"55\\n55\\n57\\n68\\n68\\n\", \"55\\n56\\n60\\n55\\n60\\n\", \"55\\n56\\n56\\n56\\n61\\n\", \"53\\n53\\n53\\n56\\n63\\n\", \"55\\n55\\n57\\n57\\n57\\n\", \"46\\n46\\n46\\n46\\n59\\n\", \"70\\n70\\n72\\n70\\n77\\n\", \"78\\n78\\n78\\n78\\n78\\n\", \"67\\n67\\n67\\n67\\n67\\n\", \"44\\n44\\n44\\n53\\n53\\n\", \"100\\n102\\n102\\n100\\n100\\n\", \"46\\n48\\n48\\n46\\n46\\n\", \"43\\n43\\n43\\n51\\n51\\n\", \"67\\n69\\n71\\n75\\n75\\n\", \"55\\n55\\n55\\n55\\n55\\n\", \"55\\n55\\n55\\n68\\n68\\n\", \"55\\n56\\n58\\n55\\n58\\n\", \"70\\n74\\n74\\n70\\n74\\n\", \"71\\n71\\n73\\n71\\n78\\n\", \"44\\n48\\n48\\n44\\n44\\n\", \"43\\n43\\n43\\n47\\n47\\n\", \"43\\n44\\n46\\n46\\n55\\n\", \"55\\n55\\n55\\n63\\n63\\n\", \"60\\n61\\n63\\n60\\n63\\n\", \"70\\n70\\n70\\n70\\n74\\n\", \"77\\n77\\n79\\n77\\n84\\n\", \"44\\n48\\n48\\n44\\n48\\n\", \"43\\n43\\n43\\n43\\n55\\n\", \"38\\n39\\n43\\n43\\n43\\n\", \"73\\n73\\n75\\n73\\n75\\n\", \"70\\n71\\n71\\n71\\n76\\n\", \"76\\n78\\n78\\n76\\n76\\n\", \"40\\n40\\n44\\n44\\n44\\n\", \"71\\n71\\n71\\n71\\n75\\n\", \"53\\n53\\n53\\n53\\n53\\n\", \"76\\n76\\n76\\n76\\n76\\n\", \"40\\n40\\n44\\n44\\n56\\n\", \"72\\n72\\n72\\n72\\n75\\n\", \"63\\n66\\n66\\n64\\n66\\n\", \"35\\n35\\n35\\n35\\n39\\n\", \"40\\n40\\n44\\n44\\n63\\n\", \"61\\n63\\n63\\n61\\n66\\n\", \"33\\n33\\n33\\n33\\n33\\n\", \"40\\n40\\n44\\n44\\n82\\n\", \"72\\n72\\n72\\n72\\n72\\n\", \"61\\n63\\n63\\n61\\n63\\n\", \"62\\n62\\n62\\n62\\n62\\n\", \"66\\n68\\n68\\n66\\n77\\n\", \"62\\n64\\n64\\n62\\n73\\n\", \"65\\n67\\n67\\n65\\n73\\n\", \"48\\n50\\n50\\n48\\n56\\n\", \"44\\n46\\n46\\n44\\n49\\n\", \"50\\n51\\n57\\n51\\n57\\n\", \"55\\n55\\n60\\n56\\n63\\n\", \"55\\n55\\n59\\n55\\n63\\n\", \"45\\n46\\n51\\n46\\n56\\n\", \"70\\n71\\n74\\n71\\n78\\n\", \"55\\n55\\n55\\n59\\n59\\n\", \"55\\n59\\n59\\n59\\n59\\n\", \"82\\n84\\n84\\n82\\n84\\n\", \"70\\n73\\n73\\n71\\n73\\n\", \"55\\n55\\n55\\n55\\n59\\n\", \"92\\n92\\n94\\n92\\n94\\n\", \"55\\n55\\n62\\n62\\n62\\n\", \"70\\n72\\n70\\n70\\n70\\n\", \"43\\n44\\n48\\n57\\n57\\n\", \"82\\n82\\n86\\n86\\n86\\n\", \"55\\n56\\n55\\n56\\n65\\n\", \"67\\n67\\n71\\n71\\n71\\n\", \"68\\n68\\n68\\n68\\n68\\n\", \"48\\n49\\n49\\n49\\n53\\n\", \"100\\n102\\n100\\n100\\n100\\n\", \"53\\n53\\n53\\n56\\n56\\n\", \"48\\n48\\n48\\n48\\n52\\n\", \"55\\n55\\n55\\n57\\n68\\n\", \"79\\n79\\n81\\n79\\n81\\n\", \"92\\n94\\n94\\n92\\n94\\n\", \"44\\n46\\n46\\n44\\n44\\n\", \"59\\n59\\n59\\n63\\n63\\n\", \"44\\n44\\n46\\n46\\n55\\n\", \"70\\n74\\n70\\n70\\n74\\n\", \"64\\n64\\n64\\n64\\n68\\n\", \"43\\n43\\n43\\n47\\n55\\n\", \"36\\n37\\n39\\n39\\n43\\n\", \"93\\n93\\n95\\n93\\n95\\n\", \"70\\n71\\n71\\n71\\n71\\n\", \"96\\n96\\n96\\n96\\n96\\n\", \"62\\n64\\n64\\n62\\n62\\n\", \"40\\n40\\n40\\n44\\n54\\n\", \"55\\n55\\n55\\n55\\n63\\n\", \"76\\n77\\n77\\n77\\n77\\n\", \"64\\n66\\n66\\n64\\n66\\n\", \"24\\n24\\n24\\n24\\n28\\n\", \"72\\n72\\n75\\n72\\n75\\n\", \"106\\n106\\n106\\n106\\n106\\n\", \"41\\n41\\n44\\n44\\n82\\n\", \"60\\n60\\n60\\n60\\n60\\n\", \"61\\n63\\n61\\n61\\n63\\n\", \"65\\n67\\n67\\n65\\n92\\n\", \"51\\n53\\n53\\n51\\n56\\n\", \"44\\n46\\n46\\n44\\n46\\n\", \"44\\n46\\n46\\n46\\n49\\n\", \"45\\n46\\n52\\n46\\n57\\n\", \"58\\n58\\n63\\n59\\n63\\n\", \"55\\n56\\n56\\n55\\n63\\n\", \"51\\n52\\n54\\n52\\n54\\n\", \"59\\n59\\n59\\n59\\n59\\n\", \"93\\n95\\n95\\n93\\n95\\n\", \"58\\n59\\n59\\n59\\n59\\n\", \"55\\n55\\n55\\n62\\n62\\n\", \"69\\n73\\n73\\n77\\n77\\n\", \"55\\n56\\n60\\n60\\n60\\n\", \"55\\n56\\n60\\n60\\n60\\n\", \"55\\n56\\n60\\n60\\n60\\n\", \"55\\n55\\n59\\n63\\n63\\n\", \"55\\n55\\n59\\n59\\n59\\n\", \"70\\n71\\n73\\n71\\n73\\n\", \"55\\n55\\n59\\n59\\n59\\n\", \"55\\n55\\n59\\n59\\n59\\n\", \"65\\n65\\n65\\n68\\n68\\n\", \"70\\n72\\n72\\n70\\n70\\n\", \"82\\n86\\n86\\n82\\n86\\n\", \"55\\n55\\n59\\n59\\n59\\n\", \"43\\n44\\n48\\n48\\n57\\n\", \"55\\n56\\n56\\n56\\n61\\n\", \"55\\n55\\n57\\n57\\n57\\n\", \"78\\n78\\n78\\n78\\n78\\n\", \"67\\n67\\n67\\n67\\n67\\n\", \"100\\n102\\n102\\n100\\n100\\n\", \"55\\n55\\n55\\n55\\n55\\n\", \"78\\n78\\n78\\n78\\n78\\n\", \"100\\n102\\n102\\n100\\n100\\n\", \"55\\n55\\n55\\n55\\n55\\n\", \"78\\n78\\n78\\n78\\n78\\n\", \"43\\n43\\n43\\n43\\n55\\n\", \"55\\n55\\n55\\n55\\n55\\n\", \"70\\n71\\n71\\n71\\n76\\n\", \"43\\n43\\n43\\n43\\n55\\n\", \"53\\n53\\n53\\n53\\n53\\n\", \"76\\n76\\n76\\n76\\n76\\n\", \"72\\n72\\n72\\n72\\n75\\n\", \"76\\n76\\n76\\n76\\n76\\n\", \"61\\n63\\n63\\n61\\n66\\n\", \"72\\n72\\n72\\n72\\n72\\n\", \"44\\n46\\n46\\n44\\n49\\n\", \"44\\n46\\n46\\n44\\n49\\n\", \"44\\n46\\n46\\n44\\n49\\n\", \"55\\n55\\n59\\n59\\n59\\n\", \"55\\n56\\n60\\n60\\n60\\n\", \"55\\n59\\n59\\n63\\n63\\n\", \"70\\n72\\n72\\n70\\n72\\n\", \"55\\n59\\n59\\n63\\n63\\n\", \"55\\n55\\n57\\n68\\n68\\n\", \"55\\n56\\n58\\n55\\n58\\n\", \"53\\n53\\n53\\n56\\n63\\n\", \"55\\n55\\n57\\n57\\n57\\n\", \"82\\n86\\n86\\n82\\n86\\n\", \"44\\n44\\n44\\n53\\n53\\n\", \"46\\n48\\n48\\n46\\n46\\n\", \"67\\n69\\n71\\n75\\n75\\n\", \"55\\n56\\n56\\n56\\n61\\n\", \"78\\n78\\n78\\n78\\n78\\n\", \"100\\n102\\n102\\n100\\n100\\n\", \"55\\n55\\n55\\n55\\n55\\n\", \"55\\n55\\n55\\n63\\n63\\n\", \"60\\n61\\n63\\n60\\n63\\n\", \"77\\n77\\n79\\n77\\n84\\n\", \"100\\n102\\n102\\n100\\n100\\n\", \"55\\n55\\n55\\n55\\n55\\n\", \"70\\n71\\n71\\n71\\n76\\n\", \"53\\n53\\n53\\n53\\n53\\n\", \"40\\n40\\n44\\n44\\n56\\n\", \"53\\n53\\n53\\n53\\n53\\n\", \"76\\n78\\n78\\n76\\n76\\n\", \"33\\n33\\n33\\n33\\n33\\n\", \"62\\n62\\n62\\n62\\n62\\n\", \"61\\n63\\n63\\n61\\n66\\n\", \"72\\n72\\n72\\n72\\n72\\n\", \"44\\n46\\n46\\n44\\n49\\n\", \"55\\n55\\n55\\n59\\n59\\n\", \"55\\n56\\n60\\n64\\n64\\n\"]}", "source": "taco"}
|
Monocarp plays a computer game (yet again!). This game has a unique trading mechanics.
To trade with a character, Monocarp has to choose one of the items he possesses and trade it for some item the other character possesses. Each item has an integer price. If Monocarp's chosen item has price $x$, then he can trade it for any item (exactly one item) with price not greater than $x+k$.
Monocarp initially has $n$ items, the price of the $i$-th item he has is $a_i$. The character Monocarp is trading with has $m$ items, the price of the $i$-th item they have is $b_i$. Monocarp can trade with this character as many times as he wants (possibly even zero times), each time exchanging one of his items with one of the other character's items according to the aforementioned constraints. Note that if Monocarp gets some item during an exchange, he can trade it for another item (since now the item belongs to him), and vice versa: if Monocarp trades one of his items for another item, he can get his item back by trading something for it.
You have to answer $q$ queries. Each query consists of one integer, which is the value of $k$, and asks you to calculate the maximum possible total cost of items Monocarp can have after some sequence of trades, assuming that he can trade an item of cost $x$ for an item of cost not greater than $x+k$ during each trade. Note that the queries are independent: the trades do not actually occur, Monocarp only wants to calculate the maximum total cost he can get.
-----Input-----
The first line contains three integers $n$, $m$ and $q$ ($1 \le n, m, q \le 2 \cdot 10^5$).
The second line contains $n$ integers $a_1, a_2, \dots, a_n$ ($1 \le a_i \le 10^9$) — the prices of the items Monocarp has.
The third line contains $m$ integers $b_1, b_2, \dots, b_m$ ($1 \le b_i \le 10^9$) — the prices of the items the other character has.
The fourth line contains $q$ integers, where the $i$-th integer is the value of $k$ for the $i$-th query ($0 \le k \le 10^9$).
-----Output-----
For each query, print one integer — the maximum possible total cost of items Monocarp can have after some sequence of trades, given the value of $k$ from the query.
-----Examples-----
Input
3 4 5
10 30 15
12 31 14 18
0 1 2 3 4
Output
55
56
60
64
64
-----Note-----
None
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4\\n0 1 1 0\\n\", \"2\\n1 1\\n\", \"1\\n0\\n\", \"4\\n0 0 0 0\\n\", \"6\\n0 0 0 0 0 1\\n\", \"20\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\\n\", \"20\\n1 1 1 0 1 0 1 1 0 1 1 1 0 1 0 0 1 1 0 0\\n\", \"1\\n1\\n\", \"2\\n0 0\\n\", \"2\\n0 1\\n\", \"2\\n1 0\\n\", \"3\\n0 0 0\\n\", \"3\\n0 0 1\\n\", \"3\\n0 1 0\\n\", \"3\\n0 1 1\\n\", \"3\\n1 0 0\\n\", \"3\\n1 0 1\\n\", \"3\\n1 1 0\\n\", \"3\\n1 1 1\\n\", \"4\\n0 0 0 1\\n\", \"4\\n0 0 1 0\\n\", \"4\\n0 0 1 1\\n\", \"4\\n0 1 0 0\\n\", \"4\\n0 1 0 1\\n\", \"4\\n0 1 1 1\\n\", \"4\\n1 0 0 0\\n\", \"4\\n1 0 0 1\\n\", \"4\\n1 0 1 0\\n\", \"4\\n1 0 1 1\\n\", \"4\\n1 1 0 0\\n\", \"4\\n1 1 0 1\\n\", \"4\\n1 1 1 0\\n\", \"4\\n1 1 1 1\\n\", \"5\\n0 0 0 0 0\\n\", \"5\\n0 0 0 0 1\\n\", \"5\\n0 0 0 1 0\\n\", \"5\\n0 0 0 1 1\\n\", \"5\\n0 0 1 0 0\\n\", \"5\\n0 0 1 0 1\\n\", \"5\\n0 0 1 1 0\\n\", \"5\\n0 0 1 1 1\\n\", \"5\\n0 1 0 0 0\\n\", \"5\\n0 1 0 0 1\\n\", \"5\\n0 1 0 1 0\\n\", \"5\\n0 1 0 1 1\\n\", \"5\\n0 1 1 0 0\\n\", \"5\\n0 1 1 0 1\\n\", \"5\\n0 1 1 1 0\\n\", \"5\\n0 1 1 1 1\\n\", \"5\\n1 0 0 0 0\\n\", \"5\\n1 0 0 0 1\\n\", \"5\\n1 0 0 1 0\\n\", \"5\\n1 0 0 1 1\\n\", \"5\\n1 0 1 0 0\\n\", \"5\\n1 0 1 0 1\\n\", \"5\\n1 0 1 1 0\\n\", \"5\\n1 0 1 1 1\\n\", \"5\\n1 1 0 0 0\\n\", \"5\\n1 1 0 0 1\\n\", \"5\\n1 1 0 1 0\\n\", \"5\\n1 1 0 1 1\\n\", \"5\\n1 1 1 0 0\\n\", \"5\\n1 1 1 0 1\\n\", \"5\\n1 1 1 1 0\\n\", \"5\\n1 1 1 1 1\\n\", \"6\\n1 1 1 1 0 0\\n\", \"6\\n0 1 1 1 0 0\\n\", \"6\\n1 1 1 0 0 0\\n\", \"6\\n0 0 0 0 0 0\\n\", \"6\\n1 0 0 1 0 0\\n\", \"6\\n1 0 1 1 0 0\\n\", \"6\\n0 0 1 1 0 0\\n\", \"6\\n0 0 0 1 0 0\\n\", \"6\\n0 0 1 0 0 0\\n\", \"200\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"40\\n1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"40\\n0 0 1 0 0 0 0 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"40\\n0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"40\\n1 1 0 1 0 1 1 1 1 1 0 1 0 0 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 1 0 1 0 0 1 0 0 0\\n\", \"45\\n0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"20\\n1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0\\n\", \"5\\n0 0 0 0 1\\n\", \"6\\n0 0 0 0 0 1\\n\", \"4\\n1 0 1 1\\n\", \"20\\n1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0\\n\", \"6\\n1 1 1 1 0 0\\n\", \"5\\n1 1 1 1 0\\n\", \"5\\n1 0 1 0 1\\n\", \"6\\n0 0 0 0 0 0\\n\", \"5\\n0 0 0 1 0\\n\", \"6\\n0 1 1 1 0 0\\n\", \"200\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"2\\n0 1\\n\", \"5\\n1 1 1 0 1\\n\", \"4\\n1 1 1 0\\n\", \"5\\n1 0 0 0 1\\n\", \"4\\n0 0 0 0\\n\", \"5\\n0 1 1 1 0\\n\", \"5\\n1 1 0 1 0\\n\", \"5\\n1 1 0 1 1\\n\", \"6\\n1 1 1 0 0 0\\n\", \"4\\n1 1 0 1\\n\", \"4\\n0 1 1 0\\n\", \"5\\n0 0 1 1 1\\n\", \"3\\n0 0 1\\n\", \"5\\n1 0 0 1 0\\n\", \"40\\n0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"4\\n1 1 1 1\\n\", \"40\\n1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"3\\n1 0 1\\n\", \"4\\n0 1 1 1\\n\", \"3\\n0 1 0\\n\", \"4\\n1 1 0 0\\n\", \"5\\n1 0 1 1 1\\n\", \"5\\n0 1 0 0 0\\n\", \"4\\n1 0 1 0\\n\", \"3\\n0 0 0\\n\", \"40\\n1 1 0 1 0 1 1 1 1 1 0 1 0 0 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 1 0 1 0 0 1 0 0 0\\n\", \"4\\n0 0 1 1\\n\", \"2\\n1 0\\n\", \"4\\n0 0 1 0\\n\", \"5\\n0 0 0 0 0\\n\", \"5\\n0 0 1 1 0\\n\", \"20\\n1 1 1 0 1 0 1 1 0 1 1 1 0 1 0 0 1 1 0 0\\n\", \"5\\n1 0 1 1 0\\n\", \"5\\n0 0 1 0 0\\n\", \"20\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\\n\", \"5\\n0 0 0 1 1\\n\", \"5\\n0 1 1 0 1\\n\", \"6\\n1 0 1 1 0 0\\n\", \"4\\n0 1 0 0\\n\", \"5\\n1 1 0 0 0\\n\", \"3\\n1 0 0\\n\", \"5\\n1 0 1 0 0\\n\", \"5\\n0 1 0 1 1\\n\", \"5\\n0 1 0 1 0\\n\", \"5\\n1 0 0 0 0\\n\", \"1\\n1\\n\", \"5\\n1 1 1 1 1\\n\", \"5\\n1 1 0 0 1\\n\", \"4\\n0 0 0 1\\n\", \"6\\n0 0 1 1 0 0\\n\", \"5\\n1 1 1 0 0\\n\", \"6\\n1 0 0 1 0 0\\n\", \"4\\n1 0 0 1\\n\", \"5\\n0 1 0 0 1\\n\", \"3\\n0 1 1\\n\", \"5\\n1 0 0 1 1\\n\", \"40\\n0 0 1 0 0 0 0 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"2\\n0 0\\n\", \"45\\n0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"4\\n1 0 0 0\\n\", \"3\\n1 1 0\\n\", \"5\\n0 1 1 1 1\\n\", \"5\\n0 1 1 0 0\\n\", \"3\\n1 1 1\\n\", \"6\\n0 0 1 0 0 0\\n\", \"4\\n0 1 0 1\\n\", \"6\\n0 0 0 1 0 0\\n\", \"5\\n0 0 1 0 1\\n\", \"5\\n1 -1 0 0 1\\n\", \"6\\n1 1 1 1 1 0\\n\", \"5\\n0 1 2 1 0\\n\", \"5\\n1 2 0 1 0\\n\", \"6\\n1 0 1 0 0 0\\n\", \"5\\n2 0 0 1 0\\n\", \"40\\n0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0\\n\", \"4\\n2 1 1 0\\n\", \"6\\n0 0 1 1 1 0\\n\", \"3\\n2 1 0\\n\", \"40\\n1 0 1 0 0 0 0 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"45\\n0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"6\\n0 0 1 0 1 0\\n\", \"6\\n1 0 0 0 0 0\\n\", \"40\\n0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0\\n\", \"4\\n3 1 1 0\\n\", \"40\\n2 0 1 0 0 0 0 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"45\\n0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"40\\n0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0\\n\", \"40\\n2 0 1 0 1 0 0 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0\\n\", \"6\\n0 0 0 0 1 1\\n\", \"4\\n-1 0 0 1\\n\", \"5\\n1 1 1 2 1\\n\", \"5\\n1 0 2 0 1\\n\", \"2\\n-1 1\\n\", \"5\\n2 1 1 0 1\\n\", \"5\\n1 1 0 2 1\\n\", \"4\\n0 2 1 1\\n\", \"5\\n0 -1 1 1 1\\n\", \"3\\n1 2 1\\n\", \"4\\n-1 2 1 1\\n\", \"4\\n-2 0 0 1\\n\", \"4\\n-1 0 1 1\\n\", \"20\\n0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\\n\", \"5\\n0 -1 0 1 1\\n\", \"5\\n1 0 0 2 1\\n\", \"3\\n0 -1 1\\n\", \"5\\n0 1 -1 1 1\\n\", \"5\\n2 0 0 0 1\\n\", \"4\\n2 0 0 1\\n\", \"5\\n0 1 1 2 1\\n\", \"5\\n-1 1 1 1 1\\n\", \"3\\n2 1 1\\n\", \"4\\n0 1 -1 1\\n\", \"2\\n2 1\\n\", \"6\\n0 0 -1 0 1 1\\n\", \"5\\n2 1 1 2 1\\n\", \"5\\n2 0 1 0 1\\n\", \"4\\n0 2 2 1\\n\", \"4\\n-1 3 1 1\\n\", \"20\\n0 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1\\n\", \"5\\n1 0 1 2 1\\n\", \"5\\n0 1 -2 1 1\\n\", \"5\\n2 1 0 0 1\\n\", \"4\\n2 0 1 1\\n\", \"5\\n0 1 0 2 1\\n\", \"5\\n-2 1 1 1 1\\n\", \"5\\n2 1 2 2 1\\n\", \"5\\n4 0 1 0 1\\n\", \"20\\n0 1 1 1 0 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1\\n\", \"5\\n1 2 1 2 1\\n\", \"5\\n0 0 -2 1 1\\n\", \"5\\n2 1 0 -1 1\\n\", \"4\\n2 0 -1 1\\n\", \"4\\n0 1 1 0\\n\", \"1\\n0\\n\", \"2\\n1 1\\n\"], \"outputs\": [\"YES\\n0->1->1->0\\n\", \"NO\\n\", \"YES\\n0\\n\", \"YES\\n0->(0->0)->0\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n1->1->1->0->1->0->1->1->0->1->1->1->0->1->0->(0->(1->1->0))->0\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n1->0\\n\", \"YES\\n(0->0)->0\\n\", \"NO\\n\", \"YES\\n0->1->0\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n1->1->0\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n0->0->1->0\\n\", \"NO\\n\", \"YES\\n(0->(1->0))->0\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n1->(0->0)->0\\n\", \"NO\\n\", \"YES\\n1->0->1->0\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n1->1->1->0\\n\", \"NO\\n\", \"YES\\n0->0->(0->0)->0\\n\", \"NO\\n\", \"YES\\n0->0->0->1->0\\n\", \"NO\\n\", \"YES\\n0->(0->(1->0))->0\\n\", \"NO\\n\", \"YES\\n0->0->1->1->0\\n\", \"NO\\n\", \"YES\\n0->1->(0->0)->0\\n\", \"NO\\n\", \"YES\\n0->1->0->1->0\\n\", \"NO\\n\", \"YES\\n(0->(1->1->0))->0\\n\", \"NO\\n\", \"YES\\n0->1->1->1->0\\n\", \"NO\\n\", \"YES\\n1->0->(0->0)->0\\n\", \"NO\\n\", \"YES\\n1->0->0->1->0\\n\", \"NO\\n\", \"YES\\n1->(0->(1->0))->0\\n\", \"NO\\n\", \"YES\\n1->0->1->1->0\\n\", \"NO\\n\", \"YES\\n1->1->(0->0)->0\\n\", \"NO\\n\", \"YES\\n1->1->0->1->0\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n1->1->1->1->0\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n(0->(1->1->1->0))->0\\n\", \"YES\\n1->1->1->(0->0)->0\\n\", \"YES\\n0->0->0->(0->0)->0\\n\", \"YES\\n1->0->(0->(1->0))->0\\n\", \"YES\\n1->(0->(1->1->0))->0\\n\", \"YES\\n0->(0->(1->1->0))->0\\n\", \"YES\\n0->0->(0->(1->0))->0\\n\", \"YES\\n0->0->1->(0->0)->0\\n\", \"NO\\n\", \"YES\\n1->0->1->0->1->0->1->(0->(1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0))->0\\n\", \"YES\\n0->0->1->0->0->0->0->0->0->1->1->0->1->0->1->0->1->(0->(1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0))->0\\n\", \"YES\\n(0->(1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0))->0\\n\", \"YES\\n1->1->0->1->0->1->1->1->1->1->0->1->0->0->1->1->1->0->0->0->0->1->1->1->1->1->0->1->0->0->0->1->0->1->0->0->1->(0->0)->0\\n\", \"YES\\n0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->(0->0)->0\\n\", \"YES\\n1->1->1->1->1->0->0->0->0->0->1->1->1->1->1->0->0->(0->0)->0\\n\", \"NO\", \"NO\", \"NO\", \"YES\\n1->1->1->1->1->0->0->0->0->0->1->1->1->1->1->0->0->(0->0)->0\", \"NO\", \"YES\\n1->1->1->1->0\", \"NO\", \"YES\\n0->0->0->(0->0)->0\", \"YES\\n0->0->0->1->0\", \"YES\\n(0->(1->1->1->0))->0\", \"NO\", \"NO\", \"NO\", \"YES\\n1->1->1->0\", \"NO\", \"YES\\n0->(0->0)->0\", \"YES\\n0->1->1->1->0\", \"YES\\n1->1->0->1->0\", \"NO\", \"YES\\n1->1->1->(0->0)->0\", \"NO\", \"YES\\n0->1->1->0\", \"NO\", \"NO\", \"YES\\n1->0->0->1->0\", \"YES\\n(0->(1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0))->0\", \"NO\", \"YES\\n1->0->1->0->1->0->1->(0->(1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0))->0\", \"NO\", \"NO\", \"YES\\n0->1->0\", \"NO\", \"NO\", \"YES\\n0->1->(0->0)->0\", \"YES\\n1->0->1->0\", \"YES\\n(0->0)->0\", \"YES\\n1->1->0->1->0->1->1->1->1->1->0->1->0->0->1->1->1->0->0->0->0->1->1->1->1->1->0->1->0->0->0->1->0->1->0->0->1->(0->0)->0\", \"NO\", \"YES\\n1->0\", \"YES\\n0->0->1->0\", \"YES\\n0->0->(0->0)->0\", \"YES\\n0->0->1->1->0\", \"YES\\n1->1->1->0->1->0->1->1->0->1->1->1->0->1->0->(0->(1->1->0))->0\", \"YES\\n1->0->1->1->0\", \"YES\\n0->(0->(1->0))->0\", \"NO\", \"NO\", \"NO\", \"YES\\n1->(0->(1->1->0))->0\", \"YES\\n(0->(1->0))->0\", \"YES\\n1->1->(0->0)->0\", \"NO\", \"YES\\n1->(0->(1->0))->0\", \"NO\", \"YES\\n0->1->0->1->0\", \"YES\\n1->0->(0->0)->0\", \"NO\", \"NO\", \"NO\", \"NO\", \"YES\\n0->(0->(1->1->0))->0\", \"NO\", \"YES\\n1->0->(0->(1->0))->0\", \"NO\", \"NO\", \"NO\", \"NO\", \"YES\\n0->0->1->0->0->0->0->0->0->1->1->0->1->0->1->0->1->(0->(1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0))->0\", \"NO\", \"YES\\n0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->(0->0)->0\", \"YES\\n1->(0->0)->0\", \"YES\\n1->1->0\", \"NO\", \"YES\\n(0->(1->1->0))->0\", \"NO\", \"YES\\n0->0->1->(0->0)->0\", \"NO\", \"YES\\n0->0->(0->(1->0))->0\", \"NO\\n\", \"NO\\n\", \"YES\\n1->1->1->1->1->0\\n\", \"YES\\n0->1->2->1->0\\n\", \"YES\\n1->2->0->1->0\\n\", \"YES\\n1->0->1->(0->0)->0\\n\", \"YES\\n2->0->0->1->0\\n\", \"YES\\n0->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->(0->0)->0\\n\", \"YES\\n2->1->1->0\\n\", \"YES\\n0->0->1->1->1->0\\n\", \"YES\\n2->1->0\\n\", \"YES\\n1->0->1->0->0->0->0->0->0->1->1->0->1->0->1->0->1->(0->(1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0))->0\\n\", \"YES\\n0->0->1->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->(0->0)->0\\n\", \"YES\\n0->0->1->0->1->0\\n\", \"YES\\n1->0->0->(0->0)->0\\n\", \"YES\\n0->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0->1->1->1->1->1->1->1->1->(0->0)->0\\n\", \"YES\\n3->1->1->0\\n\", \"YES\\n2->0->1->0->0->0->0->0->0->1->1->0->1->0->1->0->1->(0->(1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0))->0\\n\", \"YES\\n0->0->1->0->0->0->0->0->0->0->0->0->0->0->0->0->0->1->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->0->(0->0)->0\\n\", \"YES\\n0->1->1->1->1->1->1->0->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0->1->1->1->1->1->1->1->1->(0->0)->0\\n\", \"YES\\n2->0->1->0->1->0->0->0->0->1->1->0->1->0->1->0->1->(0->(1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->1->0))->0\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n0->1->1->0\", \"YES\\n0\", \"NO\"]}", "source": "taco"}
|
Implication is a function of two logical arguments, its value is false if and only if the value of the first argument is true and the value of the second argument is false.
Implication is written by using character '$\rightarrow$', and the arguments and the result of the implication are written as '0' (false) and '1' (true). According to the definition of the implication:
$0 \rightarrow 0 = 1$
$0 \rightarrow 1 = 1$
$1 \rightarrow 0 = 0$
$1 \rightarrow 1 = 1$
When a logical expression contains multiple implications, then when there are no brackets, it will be calculated from left to fight. For example,
$0 \rightarrow 0 \rightarrow 0 =(0 \rightarrow 0) \rightarrow 0 = 1 \rightarrow 0 = 0$.
When there are brackets, we first calculate the expression in brackets. For example,
$0 \rightarrow(0 \rightarrow 0) = 0 \rightarrow 1 = 1$.
For the given logical expression $a_{1} \rightarrow a_{2} \rightarrow a_{3} \rightarrow \cdots \cdots a_{n}$ determine if it is possible to place there brackets so that the value of a logical expression is false. If it is possible, your task is to find such an arrangement of brackets.
-----Input-----
The first line contains integer n (1 ≤ n ≤ 100 000) — the number of arguments in a logical expression.
The second line contains n numbers a_1, a_2, ..., a_{n} ($a_{i} \in \{0,1 \}$), which means the values of arguments in the expression in the order they occur.
-----Output-----
Print "NO" (without the quotes), if it is impossible to place brackets in the expression so that its value was equal to 0.
Otherwise, print "YES" in the first line and the logical expression with the required arrangement of brackets in the second line.
The expression should only contain characters '0', '1', '-' (character with ASCII code 45), '>' (character with ASCII code 62), '(' and ')'. Characters '-' and '>' can occur in an expression only paired like that: ("->") and represent implication. The total number of logical arguments (i.e. digits '0' and '1') in the expression must be equal to n. The order in which the digits follow in the expression from left to right must coincide with a_1, a_2, ..., a_{n}.
The expression should be correct. More formally, a correct expression is determined as follows: Expressions "0", "1" (without the quotes) are correct. If v_1, v_2 are correct, then v_1->v_2 is a correct expression. If v is a correct expression, then (v) is a correct expression.
The total number of characters in the resulting expression mustn't exceed 10^6.
If there are multiple possible answers, you are allowed to print any of them.
-----Examples-----
Input
4
0 1 1 0
Output
YES
(((0)->1)->(1->0))
Input
2
1 1
Output
NO
Input
1
0
Output
YES
0
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[\"yvvi\"], [\"Blf zoivzwb szw 10 yvvih\"], [\"Ovg'h hdrn rm gsv ulfmgzrm!\"], [{\"brand\": \"Starobrno\"}], [\"Tl slnv, blf'iv wifmp\"], [\"Hfiv r xzm wzmxv lm xlk'h xzi, slow nb yvvi\"], [true], [\"Hvv? R'n mlg gszg wifmp, r xzm hgroo gzpv nb xolgsvh luu\"], [123], [[\"Beer\"]]], \"outputs\": [[\"beer\"], [\"You already had 10 beers\"], [\"Let's swim in the fountain!\"], [\"Input is not a string\"], [\"Go home, you're drunk\"], [\"Sure i can dance on cop's car, hold my beer\"], [\"Input is not a string\"], [\"See? I'm not that drunk, i can still take my clothes off\"], [\"Input is not a string\"], [\"Input is not a string\"]]}", "source": "taco"}
|
You're hanging out with your friends in a bar, when suddenly one of them is so drunk, that he can't speak, and when he wants to say something, he writes it down on a paper. However, none of the words he writes make sense to you. He wants to help you, so he points at a beer and writes "yvvi". You start to understand what he's trying to say, and you write a script, that decodes his words.
Keep in mind that numbers, as well as other characters, can be part of the input, and you should keep them like they are. You should also test if the input is a string. If it is not, return "Input is not a string".
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 5\\n3 4\\n7 3\\n1 8\\n1 9\\n\", \"2 1\\n1\\n1 1\\n\", \"13 12\\n1 1 1 1 1 1 1 1 1 1 1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n\", \"2 1\\n1\\n1 1\\n\", \"13 12\\n1 1 1 1 1 1 1 1 1 1 1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n1 1\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n3 4\\n7 3\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n3 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n3 1\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 5\\n3 4\\n5 3\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n3 4\\n7 3\\n1 7\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n3 4\\n7 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 2\\n3 1\\n1 10\\n3 4\\n7 3\\n1 7\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n3 4\\n6 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n2 4\\n6 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 3\\n2 4\\n9 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n3 1\\n1 3\\n2 4\\n9 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n3 1\\n1 3\\n2 4\\n5 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n3 1\\n1 3\\n2 4\\n5 2\\n1 9\\n1 7\\n\", \"2 1\\n1\\n2 1\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 5\\n3 4\\n7 3\\n1 8\\n2 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 2\\n1 10\\n3 4\\n7 3\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 4 5 7\\n3 1\\n1 10\\n3 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n3 1\\n1 10\\n3 1\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 9\\n3 4\\n7 3\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 6 5 2\\n3 1\\n1 10\\n3 4\\n7 3\\n1 7\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 5\\n6 4\\n7 3\\n1 8\\n2 9\\n\", \"9 6\\n1 1 1 3 5 4 5 8\\n3 1\\n1 10\\n3 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n5 1\\n1 10\\n3 1\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 10\\n3 4\\n6 2\\n1 8\\n2 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 3\\n1 4\\n9 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n3 1\\n1 6\\n2 8\\n5 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 3\\n1 3\\n9 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 5\\n5 4\\n7 3\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 4 2 8\\n3 1\\n2 10\\n3 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n5 1\\n1 10\\n6 1\\n9 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 3\\n1 3\\n9 2\\n1 3\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 5\\n3 1\\n1 5\\n5 4\\n7 3\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n3 1\\n1 10\\n6 1\\n9 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 3\\n2 3\\n9 2\\n1 3\\n1 7\\n\", \"9 6\\n1 1 1 3 5 4 4 8\\n3 1\\n3 10\\n3 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n3 1\\n1 10\\n6 1\\n9 2\\n1 8\\n1 5\\n\", \"9 6\\n1 1 1 3 5 6 5 7\\n3 1\\n1 5\\n3 4\\n5 3\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n6 4\\n7 3\\n1 7\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n2 4\\n6 2\\n1 4\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n2 1\\n8 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 4 5 3 5 7\\n3 1\\n1 10\\n2 4\\n9 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 4 5 7\\n3 1\\n1 10\\n3 4\\n7 2\\n1 9\\n1 9\\n\", \"9 6\\n1 2 1 3 5 3 1 7\\n3 1\\n1 10\\n3 4\\n7 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 3\\n2 4\\n1 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 3 8\\n3 1\\n1 3\\n2 8\\n5 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 3\\n1 4\\n9 2\\n1 8\\n2 7\\n\", \"9 6\\n1 2 1 3 5 3 5 7\\n3 1\\n1 9\\n3 4\\n7 5\\n1 3\\n1 9\\n\", \"9 6\\n1 1 1 3 5 4 2 8\\n3 1\\n2 10\\n1 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 3\\n1 3\\n9 2\\n1 5\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n2 4\\n8 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n2 4\\n9 2\\n1 8\\n1 7\\n\", \"9 6\\n1 2 1 3 5 3 5 7\\n3 1\\n1 10\\n3 4\\n7 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 10\\n3 4\\n6 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 10\\n2 4\\n6 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 3\\n2 4\\n9 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n3 1\\n1 3\\n2 8\\n5 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 9\\n3 4\\n7 5\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 6 5 2\\n3 1\\n1 10\\n3 4\\n7 4\\n1 7\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 5\\n5 4\\n7 3\\n1 8\\n2 9\\n\", \"9 6\\n1 1 1 3 5 4 5 8\\n3 1\\n2 10\\n3 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n5 1\\n1 10\\n3 1\\n9 2\\n1 8\\n1 9\\n\", \"9 6\\n1 2 1 3 5 3 5 7\\n3 1\\n1 9\\n3 4\\n7 5\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 6 5 2\\n3 1\\n1 10\\n3 4\\n9 4\\n1 7\\n1 9\\n\", \"9 6\\n1 1 1 3 5 4 2 8\\n3 1\\n3 10\\n3 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 4 4 8\\n3 1\\n3 15\\n3 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 4 4 8\\n3 1\\n3 15\\n6 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 10\\n3 4\\n7 3\\n1 8\\n1 17\\n\", \"9 6\\n1 1 1 3 5 3 5 3\\n3 1\\n1 10\\n3 4\\n7 3\\n1 7\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 3\\n2 8\\n9 2\\n1 8\\n1 7\\n\", \"9 6\\n1 1 1 3 5 6 5 2\\n3 1\\n1 10\\n3 4\\n7 5\\n1 7\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n2 10\\n2 4\\n6 2\\n1 3\\n1 7\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 5\\n6 3\\n7 3\\n1 8\\n2 9\\n\", \"9 6\\n1 1 1 3 5 4 1 8\\n3 1\\n1 10\\n3 4\\n7 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 8\\n5 1\\n1 11\\n6 1\\n9 2\\n1 8\\n1 9\\n\", \"9 6\\n1 1 1 3 5 3 5 7\\n3 1\\n1 5\\n3 4\\n7 3\\n1 8\\n1 9\\n\"], \"outputs\": [\"3\\n6\\n8\\n-1\\n9\\n4\\n\", \"1\\n\", \"1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"1\\n\", \"1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"3\\n-1\\n8\\n-1\\n9\\n4\\n\", \"3\\n-1\\n8\\n9\\n9\\n4\\n\", \"3\\n-1\\n3\\n9\\n9\\n4\\n\", \"3\\n6\\n8\\n8\\n9\\n4\\n\", \"3\\n-1\\n8\\n-1\\n7\\n4\\n\", \"3\\n-1\\n8\\n9\\n9\\n7\\n\", \"3\\n-1\\n8\\n-1\\n8\\n4\\n\", \"3\\n-1\\n8\\n-1\\n9\\n7\\n\", \"3\\n-1\\n-1\\n-1\\n9\\n7\\n\", \"3\\n3\\n-1\\n-1\\n9\\n7\\n\", \"3\\n3\\n-1\\n-1\\n7\\n9\\n\", \"3\\n3\\n-1\\n6\\n7\\n9\\n\", \"3\\n3\\n-1\\n6\\n4\\n9\\n\", \"2\\n\", \"3\\n6\\n8\\n-1\\n9\\n-1\\n\", \"5\\n-1\\n8\\n-1\\n9\\n4\\n\", \"3\\n-1\\n8\\n9\\n7\\n9\\n\", \"3\\n-1\\n3\\n-1\\n7\\n4\\n\", \"3\\n4\\n8\\n-1\\n9\\n4\\n\", \"3\\n-1\\n7\\n-1\\n7\\n4\\n\", \"3\\n6\\n-1\\n-1\\n9\\n-1\\n\", \"3\\n-1\\n8\\n-1\\n4\\n7\\n\", \"5\\n-1\\n3\\n-1\\n7\\n4\\n\", \"3\\n-1\\n8\\n-1\\n9\\n-1\\n\", \"3\\n-1\\n5\\n-1\\n9\\n7\\n\", \"3\\n8\\n-1\\n6\\n7\\n9\\n\", \"3\\n-1\\n3\\n-1\\n9\\n7\\n\", \"3\\n6\\n-1\\n-1\\n9\\n4\\n\", \"3\\n-1\\n-1\\n-1\\n4\\n7\\n\", \"5\\n-1\\n6\\n-1\\n7\\n4\\n\", \"3\\n-1\\n3\\n-1\\n3\\n7\\n\", \"3\\n6\\n9\\n-1\\n7\\n4\\n\", \"3\\n-1\\n6\\n-1\\n7\\n4\\n\", \"3\\n-1\\n-1\\n-1\\n3\\n7\\n\", \"3\\n-1\\n-1\\n-1\\n8\\n9\\n\", \"3\\n-1\\n6\\n-1\\n7\\n6\\n\", \"3\\n6\\n7\\n7\\n8\\n4\\n\", \"3\\n-1\\n-1\\n-1\\n7\\n4\\n\", \"3\\n-1\\n-1\\n-1\\n5\\n7\\n\", \"3\\n-1\\n2\\n-1\\n9\\n7\\n\", \"3\\n-1\\n-1\\n-1\\n6\\n5\\n\", \"3\\n-1\\n8\\n9\\n9\\n9\\n\", \"3\\n-1\\n7\\n9\\n4\\n9\\n\", \"3\\n-1\\n-1\\n2\\n9\\n7\\n\", \"3\\n3\\n-1\\n6\\n9\\n8\\n\", \"3\\n-1\\n5\\n-1\\n9\\n-1\\n\", \"3\\n4\\n8\\n-1\\n3\\n4\\n\", \"3\\n-1\\n9\\n-1\\n4\\n7\\n\", \"3\\n-1\\n3\\n-1\\n6\\n7\\n\", \"3\\n-1\\n-1\\n-1\\n9\\n7\\n\", \"3\\n-1\\n-1\\n-1\\n9\\n7\\n\", \"3\\n-1\\n8\\n9\\n9\\n7\\n\", \"3\\n-1\\n8\\n-1\\n9\\n7\\n\", \"3\\n-1\\n-1\\n-1\\n9\\n7\\n\", \"3\\n-1\\n-1\\n-1\\n9\\n7\\n\", \"3\\n3\\n-1\\n6\\n7\\n9\\n\", \"3\\n4\\n8\\n-1\\n9\\n4\\n\", \"3\\n-1\\n7\\n-1\\n7\\n4\\n\", \"3\\n6\\n-1\\n-1\\n9\\n-1\\n\", \"3\\n-1\\n8\\n-1\\n4\\n7\\n\", \"5\\n-1\\n3\\n-1\\n7\\n4\\n\", \"3\\n4\\n8\\n-1\\n9\\n4\\n\", \"3\\n-1\\n7\\n-1\\n7\\n4\\n\", \"3\\n-1\\n-1\\n-1\\n4\\n7\\n\", \"3\\n-1\\n-1\\n-1\\n8\\n9\\n\", \"3\\n-1\\n-1\\n-1\\n8\\n9\\n\", \"3\\n-1\\n8\\n-1\\n9\\n-1\\n\", \"3\\n-1\\n8\\n-1\\n7\\n4\\n\", \"3\\n3\\n-1\\n-1\\n9\\n7\\n\", \"3\\n-1\\n7\\n-1\\n7\\n4\\n\", \"3\\n-1\\n-1\\n-1\\n3\\n7\\n\", \"3\\n6\\n-1\\n-1\\n9\\n-1\\n\", \"3\\n-1\\n-1\\n-1\\n8\\n9\\n\", \"5\\n-1\\n6\\n-1\\n7\\n4\\n\", \"3\\n6\\n8\\n-1\\n9\\n4\\n\"]}", "source": "taco"}
|
In this problem you will have to help Berland army with organizing their command delivery system.
There are $n$ officers in Berland army. The first officer is the commander of the army, and he does not have any superiors. Every other officer has exactly one direct superior. If officer $a$ is the direct superior of officer $b$, then we also can say that officer $b$ is a direct subordinate of officer $a$.
Officer $x$ is considered to be a subordinate (direct or indirect) of officer $y$ if one of the following conditions holds: officer $y$ is the direct superior of officer $x$; the direct superior of officer $x$ is a subordinate of officer $y$.
For example, on the picture below the subordinates of the officer $3$ are: $5, 6, 7, 8, 9$.
The structure of Berland army is organized in such a way that every officer, except for the commander, is a subordinate of the commander of the army.
Formally, let's represent Berland army as a tree consisting of $n$ vertices, in which vertex $u$ corresponds to officer $u$. The parent of vertex $u$ corresponds to the direct superior of officer $u$. The root (which has index $1$) corresponds to the commander of the army.
Berland War Ministry has ordered you to give answers on $q$ queries, the $i$-th query is given as $(u_i, k_i)$, where $u_i$ is some officer, and $k_i$ is a positive integer.
To process the $i$-th query imagine how a command from $u_i$ spreads to the subordinates of $u_i$. Typical DFS (depth first search) algorithm is used here.
Suppose the current officer is $a$ and he spreads a command. Officer $a$ chooses $b$ — one of his direct subordinates (i.e. a child in the tree) who has not received this command yet. If there are many such direct subordinates, then $a$ chooses the one having minimal index. Officer $a$ gives a command to officer $b$. Afterwards, $b$ uses exactly the same algorithm to spread the command to its subtree. After $b$ finishes spreading the command, officer $a$ chooses the next direct subordinate again (using the same strategy). When officer $a$ cannot choose any direct subordinate who still hasn't received this command, officer $a$ finishes spreading the command.
Let's look at the following example: [Image]
If officer $1$ spreads a command, officers receive it in the following order: $[1, 2, 3, 5 ,6, 8, 7, 9, 4]$.
If officer $3$ spreads a command, officers receive it in the following order: $[3, 5, 6, 8, 7, 9]$.
If officer $7$ spreads a command, officers receive it in the following order: $[7, 9]$.
If officer $9$ spreads a command, officers receive it in the following order: $[9]$.
To answer the $i$-th query $(u_i, k_i)$, construct a sequence which describes the order in which officers will receive the command if the $u_i$-th officer spreads it. Return the $k_i$-th element of the constructed list or -1 if there are fewer than $k_i$ elements in it.
You should process queries independently. A query doesn't affect the following queries.
-----Input-----
The first line of the input contains two integers $n$ and $q$ ($2 \le n \le 2 \cdot 10^5, 1 \le q \le 2 \cdot 10^5$) — the number of officers in Berland army and the number of queries.
The second line of the input contains $n - 1$ integers $p_2, p_3, \dots, p_n$ ($1 \le p_i < i$), where $p_i$ is the index of the direct superior of the officer having the index $i$. The commander has index $1$ and doesn't have any superiors.
The next $q$ lines describe the queries. The $i$-th query is given as a pair ($u_i, k_i$) ($1 \le u_i, k_i \le n$), where $u_i$ is the index of the officer which starts spreading a command, and $k_i$ is the index of the required officer in the command spreading sequence.
-----Output-----
Print $q$ numbers, where the $i$-th number is the officer at the position $k_i$ in the list which describes the order in which officers will receive the command if it starts spreading from officer $u_i$. Print "-1" if the number of officers which receive the command is less than $k_i$.
You should process queries independently. They do not affect each other.
-----Example-----
Input
9 6
1 1 1 3 5 3 5 7
3 1
1 5
3 4
7 3
1 8
1 9
Output
3
6
8
-1
9
4
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.75
|
{"tests": "{\"inputs\": [\"7\\nbanana\\nta\\ntomb\\nbus\\nsound\\ndoes\\nsome\", \"7\\nananab\\nta\\nsomb\\nbus\\nsound\\ndoes\\nsemo\", \"7\\nbanaoa\\nta\\ntomb\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanaoa\\nta\\nuomb\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanaoa\\nua\\ntomb\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanaoa\\nua\\ntomb\\nbus\\nspund\\ndoes\\nsome\", \"7\\nbanaoa\\nua\\ntomb\\nbus\\nspund\\nseod\\nsome\", \"7\\nbanaoa\\nua\\ntomb\\nbus\\nspund\\nsepd\\nsome\", \"7\\nbanaoa\\nva\\ntomb\\nbus\\nspund\\nsepd\\nsome\", \"7\\nbanana\\nat\\ntomb\\nbus\\nsound\\ndoes\\nsemo\", \"7\\nbanana\\nta\\ntomb\\nbus\\nsound\\ndoes\\nspme\", \"7\\nbanaoa\\nta\\ntomb\\nbus\\nsoune\\ndoes\\nsome\", \"7\\nbanaoa\\nta\\nuomb\\nbus\\nsound\\ndoes\\nsnme\", \"7\\nbamaoa\\nua\\ntomb\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanoaa\\nua\\ntomb\\nbus\\nspund\\nsepd\\nsome\", \"7\\nbanana\\nta\\ntomb\\nbus\\nsound\\ndoes\\nsemo\", \"7\\nbaanna\\nta\\ntomb\\nbus\\nsound\\ndoes\\nspme\", \"7\\nbanaoa\\nta\\ntomb\\nbus\\nsoune\\nseod\\nsome\", \"7\\nbanaoa\\ntb\\nuomb\\nbus\\nsound\\ndoes\\nsnme\", \"7\\nbamaoa\\nau\\ntomb\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanoaa\\nua\\ntomb\\nbvs\\nspund\\nsepd\\nsome\", \"7\\nbanana\\nta\\nsomb\\nbus\\nsound\\ndoes\\nsemo\", \"7\\nbanaoa\\nta\\ntobm\\nbus\\nsoune\\nseod\\nsome\", \"7\\nbanaoa\\ntb\\nbmou\\nbus\\nsound\\ndoes\\nsnme\", \"7\\nbamaoa\\nua\\ntomb\\nbus\\nsound\\ndofs\\nsome\", \"7\\nbanoaa\\nua\\ntomb\\nbvs\\nspund\\ndpes\\nsome\", \"7\\nbanana\\nta\\nbmos\\nbus\\nsound\\ndoes\\nsemo\", \"7\\nbanaoa\\nta\\ntobm\\nbus\\nseuno\\nseod\\nsome\", \"7\\nbamaob\\nua\\ntomb\\nbus\\nsound\\ndofs\\nsome\", \"7\\nbanana\\nta\\nbmos\\nbus\\nsound\\ndoet\\nsemo\", \"7\\nbamboa\\nua\\ntomb\\nbus\\nsound\\ndofs\\nsome\", \"7\\nbanana\\nta\\nbmos\\nbur\\nsound\\ndoet\\nsemo\", \"7\\nbanana\\nat\\ntbmo\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanaoa\\nta\\nbmot\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanaoa\\nta\\nuomb\\nbus\\nspund\\ndoes\\nsome\", \"7\\nbanaao\\nua\\ntomb\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanana\\nta\\ntolb\\nbus\\nsound\\ndoes\\nspme\", \"7\\nbanoaa\\nua\\ntomb\\nbus\\nspund\\nsfpd\\nsome\", \"7\\nbaanna\\nta\\ntomb\\nbus\\nsound\\neods\\nspme\", \"7\\nbonaaa\\nta\\ntomb\\nbus\\nsoune\\nseod\\nsome\", \"7\\nbanaoa\\ntb\\nuomb\\nbus\\nsound\\ndoes\\nsnmd\", \"7\\nbamaoa\\nau\\ntomb\\nbus\\nspund\\ndoes\\nsome\", \"7\\nbanoaa\\nau\\ntomb\\nbvs\\nspund\\nsepd\\nsome\", \"7\\nbanaoa\\nta\\ntobm\\nbus\\nsouen\\nseod\\nsome\", \"7\\nbanaoa\\ntb\\nbmou\\nbus\\nsound\\ndoes\\nsmne\", \"7\\nbamaoa\\nva\\ntomb\\nbus\\nsound\\ndofs\\nsome\", \"7\\nbaoana\\nta\\nbmos\\nbus\\nsound\\ndoes\\nsemo\", \"7\\nbanao`\\nta\\ntobm\\nbus\\nseuno\\nseod\\nsome\", \"7\\nbanana\\nta\\nbmos\\nbus\\nsound\\ndnet\\nsemo\", \"7\\nbamboa\\nua\\nmotb\\nbus\\nsound\\ndofs\\nsome\", \"7\\nbanana\\nta\\ntbmo\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanaao\\nua\\ntomb\\nbus\\nsound\\ndoes\\nsnme\", \"7\\nbanana\\nat\\ntolb\\nbus\\nsound\\ndoes\\nspme\", \"7\\nbaanna\\nta\\ntomb\\nbus\\nsound\\nsdoe\\nspme\", \"7\\nbonaaa\\nta\\ntomb\\nbus\\nsouoe\\nseod\\nsome\", \"7\\nbanaoa\\ntb\\nuomb\\nbus\\nsound\\ndpes\\nsnmd\", \"7\\nbamaoa\\nau\\ntomb\\nbvs\\nspund\\ndoes\\nsome\", \"7\\nbaooaa\\nau\\ntomb\\nbvs\\nspund\\nsepd\\nsome\", \"7\\nananab\\nta\\nsomb\\nbus\\nsound\\nseod\\nsemo\", \"7\\nbanaoa\\nta\\ntobm\\nbus\\nsouem\\nseod\\nsome\", \"7\\nbanaoa\\ntb\\nbmou\\nbus\\nspund\\ndoes\\nsmne\", \"7\\nbboana\\nta\\nbmos\\nbus\\nsound\\ndoes\\nsemo\", \"7\\nbanao`\\nta\\ntobm\\nbus\\nseuno\\nseod\\nsone\", \"7\\nbamboa\\nua\\nbtom\\nbus\\nsound\\ndofs\\nsome\", \"7\\nbanana\\nta\\ntbmo\\nbus\\nsound\\nseod\\nsome\", \"7\\nbonaaa\\nta\\ntomb\\nbus\\nsouoe\\nseoc\\nsome\", \"7\\nbanaoa\\ntb\\nubmo\\nbus\\nsound\\ndpes\\nsnmd\", \"7\\nbamaoa\\nau\\ntomb\\nbvs\\nspund\\ndoes\\nsnme\", \"7\\nbaooaa\\nua\\ntomb\\nbvs\\nspund\\nsepd\\nsome\", \"7\\nananab\\nta\\nsomb\\nbus\\nsounc\\nseod\\nsemo\", \"7\\nbaoaoa\\nta\\ntobm\\nbus\\nsouen\\nseod\\nsome\", \"7\\nbboana\\nta\\nbmos\\nbus\\nsound\\nseod\\nsemo\", \"7\\nbanao`\\nta\\ntobm\\nbus\\nsueno\\nseod\\nsone\", \"7\\nbanana\\nta\\ntbmo\\nbus\\nsound\\nseod\\nsole\", \"7\\nbanaoa\\ntb\\nubmo\\nbus\\nsound\\nsepd\\nsnmd\", \"7\\nbamao`\\nau\\ntomb\\nbvs\\nspund\\ndoes\\nsnme\", \"7\\nbaooaa\\nau\\ntomb\\nbvs\\nspund\\nsepd\\nsnme\", \"7\\nananab\\nta\\nsomb\\nbus\\nnousc\\nseod\\nsemo\", \"7\\nbaoaoa\\nta\\ntocm\\nbus\\nsouen\\nseod\\nsome\", \"7\\nbanao`\\nat\\ntobm\\nbus\\nsueno\\nseod\\nsone\", \"7\\nbanana\\nua\\ntbmo\\nbus\\nsound\\nseod\\nsole\", \"7\\nbanaoa\\ntb\\nubmo\\nbus\\nsound\\nsepc\\nsnmd\", \"7\\nananab\\nta\\nsomb\\nbus\\nnousc\\nseod\\nseno\", \"7\\nbaoaoa\\nta\\ntocl\\nbus\\nsouen\\nseod\\nsome\", \"7\\nbanao`\\nat\\ntobm\\nbus\\nsudno\\nseod\\nsone\", \"7\\nbanaoa\\ntb\\nubmp\\nbus\\nsound\\nsepc\\nsnmd\", \"7\\nbaoaoa\\nsa\\ntocl\\nbus\\nsouen\\nseod\\nsome\", \"7\\nbanao`\\nat\\nmbot\\nbus\\nsudno\\nseod\\nsone\", \"7\\nbanaoa\\ntb\\nubmp\\nbus\\nsound\\nsdpc\\nsnmd\", \"7\\nbaoaoa\\nsa\\ntocl\\nbus\\nneuos\\nseod\\nsome\", \"7\\nbanaoa\\ntb\\nubmp\\nbus\\nsound\\nscpd\\nsnmd\", \"7\\nbaoaoa\\nsa\\ncotl\\nbus\\nneuos\\nseod\\nsome\", \"7\\nbanana\\nta\\ntomb\\nbus\\nsound\\ndseo\\nsome\", \"7\\nbanaoa\\nta\\ntomb\\nbus\\nsound\\ndoes\\nsomd\", \"7\\nbanaoa\\nua\\nbomt\\nbus\\nsound\\ndoes\\nsome\", \"7\\nbanaoa\\nva\\ntomb\\nbus\\nspund\\ndoes\\nsome\", \"7\\nbanaoa\\nua\\nbmot\\nbus\\nspund\\nseod\\nsome\", \"7\\nbanaoa\\nua\\nsomb\\nbus\\nspund\\nsepd\\nsome\", \"7\\nbanaoa\\nvb\\ntomb\\nbus\\nspund\\nsepd\\nsome\", \"7\\nbanana\\nau\\ntomb\\nbus\\nsound\\ndoes\\nsemo\", \"7\\nbanana\\nat\\ntomb\\nbus\\nsound\\ndoes\\nsome\"], \"outputs\": [\"2\\n\", \"3\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\\n\", \"2\"]}", "source": "taco"}
|
D: Shiritori Compression
problem
Ebi-chan and Kana-chan did a shiritori. Ebi-chan is looking at the memo of the word that came out in Shiritori.
Ebi-chan wants to remove redundant continuous subsequences from this word sequence w_1, w_2, ..., w_N until they no longer exist. The redundant continuous subsequence that Ebi-chan thinks is defined as follows.
* The continuous subsequence w_i, ..., w_ {j-1} is redundant when i, j satisfying the following is present.
* For the subscripts i, j with i <j, the first letters of the words w_i and w_j are equal.
At this time, Ebi-chan removes words with subscript i or more and j-1 or less.
For example, consider the following word string:
* apple → editor → random → me → edge
It is compressed as follows:
* apple → edge
Since the first letter of editor and edge matches with e, the words from editor to just before edge (me) are stripped.
Please note that Ebi-chan's criteria do not consider the same trailing character to be redundant. For example, in the compressed word string above, the last letter of apple and edge is both e, but this does not remove the word.
The following examples are also possible.
* orange → eel → luck
* banana → at → tomb → bus → sound → does → some
* peach → hero → owl → loop → proof → fish → he
Each of these can be compressed as follows: Note that in each case, the last word is saved.
* orange → eel → luck
* Already compressed.
* bus → some
* You can compress banana to bus and sound to some.
* peach → he
* You can also compress proof → fish → he, but note that the number of words after compression is different.
Ebi-chan's memos are given, so please output the minimum value L of the length (number of words) of the word string obtained by compressing them.
You can assume that "the same word appears multiple times" or "the first letter of a word does not match the last letter of the previous word" does not occur.
Input format
N
w_1
...
w_N
The number of words N is given on the first line, and the i-th word is given on the 1 + i line.
Constraint
* 1 \ leq N \ leq 10 ^ 5
* 1 \ leq $ \ sum_ {i = 1} ^ N $ | w_i | \ leq 10 ^ 6
* Each letter of w_i is lowercase
Output format
Print L on one line. No other extra characters should be included.
Input example 1
7
banana
at
tomb
bus
sound
does does
some
Output example 1
2
This is the example given above.
Input example 2
7
peach
hero
owl
loop
proof
fish
he
Output example 2
2
Another example given above.
Example
Input
7
banana
at
tomb
bus
sound
does
some
Output
2
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.375
|
{"tests": "{\"inputs\": [\"2\\n2 1\\n\", \"3\\n1 2\\n3 2\\n\", \"6\\n1 5\\n3 4\\n6 1\\n3 2\\n3 1\\n\", \"4\\n4 3\\n4 1\\n4 2\\n\", \"5\\n4 1\\n4 5\\n1 2\\n1 3\\n\", \"7\\n5 7\\n2 5\\n2 1\\n1 6\\n3 6\\n4 1\\n\", \"8\\n8 6\\n7 4\\n8 5\\n2 7\\n3 2\\n5 2\\n1 2\\n\", \"9\\n3 1\\n2 7\\n9 2\\n2 1\\n6 9\\n8 9\\n9 5\\n2 4\\n\", \"10\\n2 8\\n5 10\\n3 4\\n1 6\\n3 9\\n1 7\\n4 8\\n10 8\\n1 8\\n\", \"20\\n10 20\\n11 8\\n1 11\\n10 7\\n6 14\\n17 15\\n17 13\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 6\\n4 13\\n2 1\\n\", \"50\\n21 10\\n30 22\\n3 37\\n37 32\\n4 27\\n18 7\\n2 30\\n29 19\\n6 37\\n12 39\\n47 25\\n41 49\\n45 9\\n25 48\\n16 14\\n9 7\\n33 28\\n3 31\\n34 16\\n35 37\\n27 40\\n45 16\\n29 44\\n16 15\\n26 15\\n1 12\\n2 13\\n15 21\\n43 14\\n9 33\\n44 15\\n46 1\\n38 5\\n15 5\\n1 32\\n42 35\\n20 27\\n23 8\\n1 16\\n15 17\\n36 50\\n13 8\\n49 45\\n11 2\\n24 4\\n36 15\\n15 30\\n16 4\\n25 37\\n\", \"4\\n1 2\\n2 3\\n3 4\\n\", \"9\\n3 6\\n5 2\\n5 8\\n9 5\\n1 3\\n4 9\\n7 4\\n2 3\\n\", \"10\\n1 10\\n7 1\\n6 2\\n1 3\\n8 4\\n1 9\\n1 4\\n1 6\\n5 1\\n\", \"10\\n4 3\\n2 6\\n10 1\\n5 7\\n5 8\\n10 6\\n5 9\\n9 3\\n2 9\\n\", \"11\\n1 3\\n1 8\\n1 10\\n9 2\\n1 11\\n1 4\\n2 6\\n5 1\\n7 1\\n1 2\\n\", \"11\\n5 1\\n4 7\\n8 11\\n2 6\\n3 6\\n2 10\\n4 10\\n5 4\\n11 9\\n6 11\\n\", \"12\\n1 9\\n11 1\\n1 7\\n8 1\\n2 1\\n5 12\\n1 6\\n1 12\\n3 12\\n4 12\\n12 10\\n\", \"12\\n8 12\\n2 4\\n10 11\\n6 9\\n1 3\\n7 12\\n11 12\\n8 4\\n7 9\\n5 3\\n5 6\\n\", \"9\\n8 1\\n1 4\\n1 5\\n6 1\\n2 1\\n3 1\\n9 1\\n7 1\\n\", \"11\\n9 7\\n8 4\\n9 3\\n6 3\\n7 11\\n4 2\\n9 5\\n1 9\\n4 5\\n4 10\\n\", \"11\\n1 6\\n7 10\\n7 2\\n1 5\\n9 8\\n3 7\\n1 7\\n8 1\\n1 4\\n11 8\\n\", \"11\\n1 9\\n2 3\\n8 7\\n2 11\\n2 6\\n1 5\\n2 4\\n7 10\\n9 7\\n3 10\\n\", \"11\\n1 2\\n7 3\\n1 6\\n11 3\\n8 1\\n9 1\\n5 1\\n3 4\\n1 3\\n3 10\\n\", \"12\\n12 6\\n6 10\\n2 12\\n7 6\\n11 5\\n5 6\\n11 8\\n3 11\\n4 7\\n3 1\\n7 9\\n\", \"13\\n3 6\\n1 5\\n3 2\\n1 11\\n1 7\\n1 8\\n1 9\\n1 12\\n9 4\\n3 1\\n13 1\\n10 1\\n\", \"14\\n9 2\\n12 14\\n3 14\\n9 3\\n5 14\\n5 13\\n7 10\\n8 11\\n13 7\\n12 6\\n8 6\\n4 8\\n1 4\\n\", \"15\\n1 8\\n11 4\\n1 12\\n1 14\\n12 2\\n4 13\\n4 10\\n4 1\\n1 9\\n15 1\\n1 7\\n1 5\\n4 6\\n4 3\\n\", \"16\\n4 10\\n13 3\\n14 3\\n5 11\\n6 16\\n1 4\\n8 10\\n16 7\\n8 9\\n3 11\\n9 2\\n15 9\\n15 12\\n12 7\\n13 7\\n\", \"17\\n17 1\\n7 1\\n16 1\\n5 1\\n9 1\\n7 4\\n14 1\\n6 1\\n11 1\\n2 1\\n7 12\\n10 1\\n3 1\\n1 13\\n15 1\\n1 8\\n\", \"10\\n2 8\\n5 10\\n3 4\\n1 6\\n3 9\\n1 7\\n4 8\\n10 8\\n1 8\\n\", \"12\\n8 12\\n2 4\\n10 11\\n6 9\\n1 3\\n7 12\\n11 12\\n8 4\\n7 9\\n5 3\\n5 6\\n\", \"15\\n1 8\\n11 4\\n1 12\\n1 14\\n12 2\\n4 13\\n4 10\\n4 1\\n1 9\\n15 1\\n1 7\\n1 5\\n4 6\\n4 3\\n\", \"4\\n4 3\\n4 1\\n4 2\\n\", \"4\\n1 2\\n2 3\\n3 4\\n\", \"9\\n8 1\\n1 4\\n1 5\\n6 1\\n2 1\\n3 1\\n9 1\\n7 1\\n\", \"11\\n1 2\\n7 3\\n1 6\\n11 3\\n8 1\\n9 1\\n5 1\\n3 4\\n1 3\\n3 10\\n\", \"8\\n8 6\\n7 4\\n8 5\\n2 7\\n3 2\\n5 2\\n1 2\\n\", \"10\\n4 3\\n2 6\\n10 1\\n5 7\\n5 8\\n10 6\\n5 9\\n9 3\\n2 9\\n\", \"17\\n17 1\\n7 1\\n16 1\\n5 1\\n9 1\\n7 4\\n14 1\\n6 1\\n11 1\\n2 1\\n7 12\\n10 1\\n3 1\\n1 13\\n15 1\\n1 8\\n\", \"11\\n1 3\\n1 8\\n1 10\\n9 2\\n1 11\\n1 4\\n2 6\\n5 1\\n7 1\\n1 2\\n\", \"13\\n3 6\\n1 5\\n3 2\\n1 11\\n1 7\\n1 8\\n1 9\\n1 12\\n9 4\\n3 1\\n13 1\\n10 1\\n\", \"11\\n1 9\\n2 3\\n8 7\\n2 11\\n2 6\\n1 5\\n2 4\\n7 10\\n9 7\\n3 10\\n\", \"7\\n5 7\\n2 5\\n2 1\\n1 6\\n3 6\\n4 1\\n\", \"16\\n4 10\\n13 3\\n14 3\\n5 11\\n6 16\\n1 4\\n8 10\\n16 7\\n8 9\\n3 11\\n9 2\\n15 9\\n15 12\\n12 7\\n13 7\\n\", \"11\\n1 6\\n7 10\\n7 2\\n1 5\\n9 8\\n3 7\\n1 7\\n8 1\\n1 4\\n11 8\\n\", \"10\\n1 10\\n7 1\\n6 2\\n1 3\\n8 4\\n1 9\\n1 4\\n1 6\\n5 1\\n\", \"9\\n3 6\\n5 2\\n5 8\\n9 5\\n1 3\\n4 9\\n7 4\\n2 3\\n\", \"9\\n3 1\\n2 7\\n9 2\\n2 1\\n6 9\\n8 9\\n9 5\\n2 4\\n\", \"14\\n9 2\\n12 14\\n3 14\\n9 3\\n5 14\\n5 13\\n7 10\\n8 11\\n13 7\\n12 6\\n8 6\\n4 8\\n1 4\\n\", \"12\\n12 6\\n6 10\\n2 12\\n7 6\\n11 5\\n5 6\\n11 8\\n3 11\\n4 7\\n3 1\\n7 9\\n\", \"6\\n1 5\\n3 4\\n6 1\\n3 2\\n3 1\\n\", \"50\\n21 10\\n30 22\\n3 37\\n37 32\\n4 27\\n18 7\\n2 30\\n29 19\\n6 37\\n12 39\\n47 25\\n41 49\\n45 9\\n25 48\\n16 14\\n9 7\\n33 28\\n3 31\\n34 16\\n35 37\\n27 40\\n45 16\\n29 44\\n16 15\\n26 15\\n1 12\\n2 13\\n15 21\\n43 14\\n9 33\\n44 15\\n46 1\\n38 5\\n15 5\\n1 32\\n42 35\\n20 27\\n23 8\\n1 16\\n15 17\\n36 50\\n13 8\\n49 45\\n11 2\\n24 4\\n36 15\\n15 30\\n16 4\\n25 37\\n\", \"12\\n1 9\\n11 1\\n1 7\\n8 1\\n2 1\\n5 12\\n1 6\\n1 12\\n3 12\\n4 12\\n12 10\\n\", \"5\\n4 1\\n4 5\\n1 2\\n1 3\\n\", \"20\\n10 20\\n11 8\\n1 11\\n10 7\\n6 14\\n17 15\\n17 13\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 6\\n4 13\\n2 1\\n\", \"11\\n9 7\\n8 4\\n9 3\\n6 3\\n7 11\\n4 2\\n9 5\\n1 9\\n4 5\\n4 10\\n\", \"11\\n5 1\\n4 7\\n8 11\\n2 6\\n3 6\\n2 10\\n4 10\\n5 4\\n11 9\\n6 11\\n\", \"12\\n8 3\\n2 4\\n10 11\\n6 9\\n1 3\\n7 12\\n11 12\\n8 4\\n7 9\\n5 3\\n5 6\\n\", \"11\\n1 2\\n7 3\\n1 6\\n11 3\\n8 1\\n9 1\\n5 1\\n3 4\\n1 3\\n2 10\\n\", \"10\\n4 3\\n2 6\\n10 1\\n5 7\\n5 8\\n10 6\\n5 9\\n9 4\\n2 9\\n\", \"13\\n4 6\\n1 5\\n3 2\\n1 11\\n1 7\\n1 8\\n1 9\\n1 12\\n9 4\\n3 1\\n13 1\\n10 1\\n\", \"11\\n1 6\\n7 10\\n7 2\\n2 5\\n9 8\\n3 7\\n1 7\\n8 1\\n1 4\\n11 8\\n\", \"20\\n10 20\\n11 8\\n2 11\\n10 7\\n6 14\\n17 15\\n17 13\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 6\\n4 13\\n2 1\\n\", \"11\\n9 7\\n8 3\\n9 3\\n6 3\\n7 11\\n4 2\\n9 5\\n1 9\\n4 5\\n4 10\\n\", \"3\\n1 2\\n3 1\\n\", \"11\\n1 2\\n7 3\\n1 6\\n11 3\\n8 1\\n9 1\\n5 1\\n3 4\\n1 4\\n2 10\\n\", \"8\\n8 6\\n7 4\\n8 5\\n2 7\\n3 2\\n5 4\\n1 2\\n\", \"10\\n4 3\\n2 6\\n10 1\\n5 7\\n5 8\\n10 3\\n5 9\\n9 3\\n2 9\\n\", \"17\\n17 1\\n7 1\\n16 1\\n5 1\\n9 1\\n7 4\\n14 1\\n6 1\\n11 1\\n2 1\\n7 12\\n10 1\\n3 2\\n1 13\\n15 1\\n1 8\\n\", \"16\\n4 10\\n13 3\\n14 1\\n5 11\\n6 16\\n1 4\\n8 10\\n16 7\\n8 9\\n3 11\\n9 2\\n15 9\\n15 12\\n12 7\\n13 7\\n\", \"10\\n2 10\\n7 1\\n6 2\\n1 3\\n8 4\\n1 9\\n1 4\\n1 6\\n5 1\\n\", \"14\\n9 2\\n12 14\\n3 14\\n9 3\\n5 14\\n5 13\\n7 10\\n8 11\\n13 7\\n12 6\\n8 5\\n4 8\\n1 4\\n\", \"5\\n4 1\\n3 5\\n1 2\\n1 3\\n\", \"20\\n10 20\\n11 8\\n1 11\\n10 7\\n6 14\\n17 15\\n17 3\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 6\\n4 13\\n2 1\\n\", \"13\\n4 6\\n1 5\\n1 2\\n1 11\\n1 7\\n1 8\\n1 9\\n1 12\\n9 4\\n3 1\\n13 1\\n10 1\\n\", \"20\\n5 20\\n11 8\\n2 11\\n10 7\\n6 14\\n17 15\\n17 13\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 6\\n4 13\\n2 1\\n\", \"11\\n4 7\\n8 3\\n9 3\\n6 3\\n7 11\\n4 2\\n9 5\\n1 9\\n4 5\\n4 10\\n\", \"8\\n8 6\\n7 4\\n8 5\\n2 4\\n3 2\\n5 2\\n1 2\\n\", \"20\\n10 20\\n11 8\\n1 11\\n10 7\\n12 14\\n17 15\\n17 3\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 6\\n4 13\\n2 1\\n\", \"10\\n4 3\\n2 6\\n10 1\\n5 7\\n7 8\\n10 6\\n5 9\\n9 4\\n1 9\\n\", \"20\\n5 20\\n11 8\\n2 11\\n10 7\\n6 14\\n17 15\\n17 13\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 4\\n4 13\\n2 1\\n\", \"20\\n5 20\\n11 8\\n3 11\\n10 7\\n6 14\\n17 15\\n17 13\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 4\\n4 13\\n2 1\\n\", \"12\\n8 12\\n2 4\\n10 7\\n6 9\\n1 3\\n7 12\\n11 12\\n8 4\\n7 9\\n5 3\\n5 6\\n\", \"15\\n1 8\\n11 4\\n1 12\\n1 14\\n12 2\\n4 13\\n5 10\\n4 1\\n1 9\\n15 1\\n1 7\\n1 5\\n4 6\\n4 3\\n\", \"4\\n1 3\\n4 1\\n4 2\\n\", \"8\\n8 6\\n7 4\\n8 5\\n2 7\\n3 2\\n5 1\\n1 2\\n\", \"10\\n4 3\\n2 6\\n9 1\\n5 7\\n5 8\\n10 6\\n5 9\\n9 3\\n2 9\\n\", \"13\\n3 6\\n1 5\\n3 2\\n1 11\\n1 7\\n1 8\\n1 9\\n1 12\\n3 4\\n3 1\\n13 1\\n10 1\\n\", \"11\\n1 9\\n2 3\\n8 7\\n3 11\\n2 6\\n1 5\\n2 4\\n7 10\\n9 7\\n3 10\\n\", \"16\\n4 10\\n13 3\\n14 3\\n5 11\\n6 16\\n1 4\\n8 10\\n16 4\\n8 9\\n3 11\\n9 2\\n15 9\\n15 12\\n12 7\\n13 7\\n\", \"11\\n1 6\\n7 10\\n7 2\\n1 5\\n9 8\\n3 7\\n1 7\\n9 1\\n1 4\\n11 8\\n\", \"9\\n3 6\\n5 1\\n5 8\\n9 5\\n1 3\\n4 9\\n7 4\\n2 3\\n\", \"20\\n7 20\\n11 8\\n1 11\\n10 7\\n6 14\\n17 15\\n17 13\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 6\\n4 13\\n2 1\\n\", \"11\\n9 7\\n8 4\\n9 6\\n6 3\\n7 11\\n4 2\\n9 5\\n1 9\\n4 5\\n4 10\\n\", \"11\\n5 1\\n4 7\\n8 11\\n2 6\\n3 8\\n2 10\\n4 10\\n5 4\\n11 9\\n6 11\\n\", \"12\\n8 3\\n2 4\\n10 11\\n6 9\\n1 3\\n7 12\\n11 9\\n8 4\\n7 9\\n5 3\\n5 6\\n\", \"11\\n1 6\\n7 10\\n7 2\\n2 5\\n9 8\\n3 7\\n1 7\\n11 1\\n1 4\\n11 8\\n\", \"10\\n7 3\\n2 6\\n10 1\\n5 7\\n5 8\\n10 6\\n5 9\\n9 4\\n1 9\\n\", \"11\\n1 6\\n4 10\\n7 2\\n3 5\\n9 8\\n3 7\\n1 7\\n8 1\\n1 4\\n11 8\\n\", \"10\\n4 3\\n2 9\\n10 1\\n5 7\\n7 8\\n10 6\\n5 9\\n9 4\\n1 9\\n\", \"20\\n5 20\\n11 8\\n2 11\\n10 7\\n6 14\\n2 15\\n17 13\\n10 1\\n5 1\\n19 13\\n19 3\\n17 1\\n17 12\\n16 18\\n6 11\\n18 8\\n9 4\\n4 13\\n2 1\\n\", \"11\\n1 2\\n7 3\\n1 6\\n11 3\\n8 1\\n9 1\\n5 1\\n2 4\\n1 3\\n1 10\\n\", \"10\\n4 3\\n2 6\\n9 1\\n2 7\\n5 8\\n10 6\\n5 9\\n9 3\\n2 9\\n\", \"11\\n1 9\\n2 3\\n8 1\\n3 11\\n2 6\\n1 5\\n2 4\\n7 10\\n9 7\\n3 10\\n\", \"11\\n1 2\\n7 3\\n1 6\\n11 3\\n8 1\\n9 1\\n5 1\\n3 4\\n1 3\\n5 10\\n\", \"10\\n4 3\\n2 6\\n10 1\\n5 7\\n5 8\\n10 6\\n5 9\\n9 4\\n1 9\\n\", \"11\\n1 6\\n7 10\\n7 2\\n3 5\\n9 8\\n3 7\\n1 7\\n8 1\\n1 4\\n11 8\\n\", \"11\\n1 2\\n7 3\\n1 6\\n11 3\\n8 1\\n9 1\\n5 1\\n2 4\\n1 3\\n3 10\\n\", \"10\\n7 3\\n2 6\\n10 1\\n5 7\\n5 8\\n10 6\\n5 9\\n9 4\\n2 9\\n\", \"2\\n2 1\\n\", \"3\\n1 2\\n3 2\\n\"], \"outputs\": [\"3\\n\", \"11\\n\", \"296\\n\", \"33\\n\", \"104\\n\", \"1001\\n\", \"2807\\n\", \"7160\\n\", \"24497\\n\", \"125985156\\n\", \"120680112\\n\", \"36\\n\", \"8789\\n\", \"21234\\n\", \"27128\\n\", \"57350\\n\", \"76748\\n\", \"151928\\n\", \"279335\\n\", \"6815\\n\", \"69551\\n\", \"56414\\n\", \"75965\\n\", \"52466\\n\", \"215486\\n\", \"510842\\n\", \"2454519\\n\", \"3832508\\n\", \"21587063\\n\", \"40030094\\n\", \"24497\\n\", \"279335\\n\", \"3832508\\n\", \"33\\n\", \"36\\n\", \"6815\\n\", \"52466\\n\", \"2807\\n\", \"27128\\n\", \"40030094\\n\", \"57350\\n\", \"510842\\n\", \"75965\\n\", \"1001\\n\", \"21587063\\n\", \"56414\\n\", \"21234\\n\", \"8789\\n\", \"7160\\n\", \"2454519\\n\", \"215486\\n\", \"296\\n\", \"120680112\\n\", \"151928\\n\", \"104\\n\", \"125985156\\n\", \"69551\\n\", \"76748\\n\", \"277793\\n\", \"56996\\n\", \"27128\\n\", \"569891\\n\", \"62513\\n\", \"249976611\\n\", \"69713\\n\", \"11\\n\", \"64791\\n\", \"3070\\n\", \"25181\\n\", \"40159082\\n\", \"23284063\\n\", \"22715\\n\", \"2292587\\n\", \"104\\n\", \"219292596\\n\", \"561863\\n\", \"371285157\\n\", \"69962\\n\", \"2807\\n\", \"328415550\\n\", \"29450\\n\", \"503718936\\n\", \"487688082\\n\", \"257003\\n\", \"4074818\\n\", \"36\\n\", \"3083\\n\", \"24497\\n\", \"468290\\n\", \"76949\\n\", \"21430221\\n\", \"62003\\n\", \"8789\\n\", \"234452310\\n\", \"69551\\n\", \"83472\\n\", \"258971\\n\", \"68291\\n\", \"27074\\n\", \"69689\\n\", \"26765\\n\", \"540214836\\n\", \"59330\\n\", \"24633\\n\", \"76442\\n\", \"56996\\n\", \"27128\\n\", \"62513\\n\", \"56996\\n\", \"27074\\n\", \"3\\n\", \"11\\n\"]}", "source": "taco"}
|
Eric is the teacher of graph theory class. Today, Eric teaches independent set and edge-induced subgraph.
Given a graph $G=(V,E)$, an independent set is a subset of vertices $V' \subset V$ such that for every pair $u,v \in V'$, $(u,v) \not \in E$ (i.e. no edge in $E$ connects two vertices from $V'$).
An edge-induced subgraph consists of a subset of edges $E' \subset E$ and all the vertices in the original graph that are incident on at least one edge in the subgraph.
Given $E' \subset E$, denote $G[E']$ the edge-induced subgraph such that $E'$ is the edge set of the subgraph. Here is an illustration of those definitions: [Image]
In order to help his students get familiar with those definitions, he leaves the following problem as an exercise:
Given a tree $G=(V,E)$, calculate the sum of $w(H)$ over all except null edge-induced subgraph $H$ of $G$, where $w(H)$ is the number of independent sets in $H$. Formally, calculate $\sum \limits_{\emptyset \not= E' \subset E} w(G[E'])$.
Show Eric that you are smarter than his students by providing the correct answer as quickly as possible. Note that the answer might be large, you should output the answer modulo $998,244,353$.
-----Input-----
The first line contains a single integer $n$ ($2 \le n \le 3 \cdot 10^5$), representing the number of vertices of the graph $G$.
Each of the following $n-1$ lines contains two integers $u$ and $v$ ($1 \le u,v \le n$, $u \not= v$), describing edges of the given tree.
It is guaranteed that the given edges form a tree.
-----Output-----
Output one integer, representing the desired value modulo $998,244,353$.
-----Examples-----
Input
2
2 1
Output
3
Input
3
1 2
3 2
Output
11
-----Note-----
For the second example, all independent sets are listed below. $\vdots : \vdots : \vdots$
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[\"a\"], [\"aaaa\"], [\"abcd\"], [\"babababababababa\"], [\"bbabbaaabbaaaabb\"], [\"123a123a123a\"], [\"123A123a123a\"], [\"12aa13a21233\"], [\"12aa13a21233A\"], [\"abcdabcaccd\"]], \"outputs\": [[\"a\"], [\"a\"], [\"abcd\"], [\"ab\"], [\"ab\"], [\"123a\"], [\"111222333Aaa\"], [\"123a\"], [\"111222333Aaaa\"], [\"aaabbccccdd\"]]}", "source": "taco"}
|
Similar to the [previous kata](https://www.codewars.com/kata/string-subpattern-recognition-ii/), but this time you need to operate with shuffled strings to identify if they are composed repeating a subpattern
Since there is no deterministic way to tell which pattern was really the original one among all the possible permutations of a fitting subpattern, return a subpattern with sorted characters, otherwise return the base string with sorted characters (you might consider this case as an edge case, with the subpattern being repeated only once and thus equalling the original input string).
For example:
```python
has_subpattern("a") == "a"; #no repeated pattern, just one character
has_subpattern("aaaa") == "a" #just one character repeated
has_subpattern("abcd") == "abcd" #base pattern equals the string itself, no repetitions
has_subpattern("babababababababa") == "ab" #remember to return the base string sorted"
has_subpattern("bbabbaaabbaaaabb") == "ab" #same as above, just shuffled
```
If you liked it, go for either the [previous kata](https://www.codewars.com/kata/string-subpattern-recognition-ii/) or the [next kata](https://www.codewars.com/kata/string-subpattern-recognition-iv/) of the series!
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"5 4\\n1 4 5 60 4\\n\", \"3 1\\n1 1 1\\n\", \"15 2\\n1 2 3 1 2 3 1 2 3 1 2 3 1 2 3\\n\", \"1 1\\n1\\n\", \"2 1\\n1 2\\n\", \"2 1\\n2 1\\n\", \"2 2\\n1 2\\n\", \"2 2\\n2 1\\n\", \"3 1\\n1 2 3\\n\", \"3 1\\n1 3 2\\n\", \"3 1\\n2 1 3\\n\", \"3 1\\n2 3 1\\n\", \"3 1\\n3 1 2\\n\", \"3 1\\n3 2 1\\n\", \"2 2\\n1 1\\n\", \"3 2\\n1 1 2\\n\", \"2 1\\n1 1\\n\", \"1 1\\n2\\n\", \"2 2\\n4 1\\n\", \"3 3\\n5 5 3\\n\", \"4 3\\n3 5 2 3\\n\", \"5 2\\n1 9 2 8 10\\n\", \"6 5\\n7 2 11 8 9 12\\n\", \"7 5\\n14 4 1 11 12 3 4\\n\", \"8 2\\n2 6 11 14 10 9 9 5\\n\", \"9 8\\n10 8 8 15 1 2 13 8 6\\n\", \"10 7\\n14 20 3 3 8 16 17 13 6 4\\n\", \"1 200000\\n1\\n\", \"1 200000\\n200000\\n\", \"1 200000\\n1\\n\", \"2 2\\n1 1\\n\", \"3 1\\n3 2 1\\n\", \"1 1\\n2\\n\", \"2 2\\n2 1\\n\", \"10 7\\n14 20 3 3 8 16 17 13 6 4\\n\", \"3 1\\n1 3 2\\n\", \"2 1\\n1 2\\n\", \"4 3\\n3 5 2 3\\n\", \"1 1\\n1\\n\", \"2 1\\n2 1\\n\", \"3 1\\n2 3 1\\n\", \"1 200000\\n200000\\n\", \"5 2\\n1 9 2 8 10\\n\", \"3 2\\n1 1 2\\n\", \"3 1\\n3 1 2\\n\", \"2 1\\n1 1\\n\", \"6 5\\n7 2 11 8 9 12\\n\", \"2 2\\n1 2\\n\", \"3 1\\n1 2 3\\n\", \"2 2\\n4 1\\n\", \"8 2\\n2 6 11 14 10 9 9 5\\n\", \"3 1\\n2 1 3\\n\", \"9 8\\n10 8 8 15 1 2 13 8 6\\n\", \"3 3\\n5 5 3\\n\", \"7 5\\n14 4 1 11 12 3 4\\n\", \"1 200000\\n0\\n\", \"2 1\\n0 1\\n\", \"3 2\\n3 2 1\\n\", \"3 1\\n1 1 2\\n\", \"3 2\\n3 1 2\\n\", \"9 8\\n10 8 8 15 1 0 13 8 6\\n\", \"15 1\\n1 2 3 1 2 3 1 2 3 1 2 3 1 2 3\\n\", \"5 4\\n1 4 5 60 5\\n\", \"15 1\\n1 2 3 0 2 3 1 2 3 1 2 3 1 2 3\\n\", \"15 1\\n1 2 3 0 2 3 1 2 3 1 2 3 2 2 3\\n\", \"1 1\\n0\\n\", \"2 2\\n0 1\\n\", \"10 7\\n14 20 3 3 15 16 17 13 6 4\\n\", \"2 1\\n0 2\\n\", \"4 0\\n3 5 2 3\\n\", \"2 2\\n2 2\\n\", \"3 1\\n2 3 0\\n\", \"5 2\\n1 9 2 8 7\\n\", \"3 0\\n1 1 2\\n\", \"2 0\\n1 1\\n\", \"6 5\\n7 2 11 2 9 12\\n\", \"2 0\\n1 2\\n\", \"3 1\\n1 1 3\\n\", \"2 2\\n4 0\\n\", \"8 1\\n2 6 11 14 10 9 9 5\\n\", \"3 1\\n2 1 2\\n\", \"3 3\\n5 6 3\\n\", \"7 5\\n14 7 1 11 12 3 4\\n\", \"3 1\\n1 0 1\\n\", \"1 1396\\n0\\n\", \"3 2\\n3 0 1\\n\", \"2 2\\n0 0\\n\", \"10 7\\n14 20 5 3 15 16 17 13 6 4\\n\", \"3 0\\n1 1 1\\n\", \"2 1\\n0 3\\n\", \"4 0\\n3 5 3 3\\n\", \"5 2\\n1 9 2 14 7\\n\", \"3 -1\\n1 1 2\\n\", \"3 4\\n3 1 2\\n\", \"2 0\\n0 1\\n\", \"6 5\\n7 2 11 2 11 12\\n\", \"2 0\\n2 2\\n\", \"2 2\\n2 0\\n\", \"8 1\\n2 6 11 14 10 9 15 5\\n\", \"3 0\\n2 1 2\\n\", \"9 8\\n10 8 8 15 0 0 13 8 6\\n\", \"3 1\\n5 6 3\\n\", \"7 5\\n14 13 1 11 12 3 4\\n\", \"3 1\\n2 0 1\\n\", \"1 1396\\n-1\\n\", \"3 0\\n3 0 1\\n\", \"2 2\\n0 2\\n\", \"10 7\\n14 20 10 3 15 16 17 13 6 4\\n\", \"3 0\\n1 1 0\\n\", \"2 2\\n0 3\\n\", \"4 0\\n3 5 6 3\\n\", \"3 -1\\n1 2 2\\n\", \"2 0\\n-1 1\\n\", \"6 5\\n7 2 11 4 11 12\\n\", \"8 1\\n2 6 11 14 10 17 15 5\\n\", \"3 0\\n2 1 1\\n\", \"9 8\\n10 8 8 10 0 0 13 8 6\\n\", \"3 2\\n5 6 3\\n\", \"7 5\\n21 13 1 11 12 3 4\\n\", \"3 1\\n2 1 1\\n\", \"1 1396\\n-2\\n\", \"15 2\\n1 2 3 1 2 3 1 2 3 1 2 3 1 2 3\\n\", \"5 4\\n1 4 5 60 4\\n\", \"3 1\\n1 1 1\\n\"], \"outputs\": [\"8\\n\", \"6\\n\", \"97\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"1\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"3\\n\", \"2\\n\", \"3\\n\", \"2\\n\", \"0\\n\", \"1\\n\", \"3\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"6\\n\", \"5\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"27\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"2\\n\", \"2\\n\", \"6\\n\", \"1\\n\", \"2\\n\", \"2\\n\", \"1\\n\", \"5\\n\", \"1\\n\", \"3\\n\", \"3\\n\", \"0\\n\", \"1\\n\", \"2\\n\", \"0\\n\", \"2\\n\", \"3\\n\", \"27\\n\", \"2\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"3\\n\", \"5\\n\", \"2\\n\", \"27\\n\", \"18\\n\", \"4\\n\", \"15\\n\", \"11\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"3\\n\", \"0\\n\", \"5\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"5\\n\", \"0\\n\", \"0\\n\", \"3\\n\", \"2\\n\", \"0\\n\", \"3\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"5\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"0\\n\", \"1\\n\", \"0\\n\", \"0\\n\", \"27\\n\", \"0\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"3\\n\", \"1\\n\", \"0\\n\", \"2\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"27\\n\", \"0\\n\", \"0\\n\", \"5\\n\", \"0\\n\", \"97\\n\", \"8\\n\", \"6\\n\"]}", "source": "taco"}
|
You are given an integer sequence $a_1, a_2, \dots, a_n$.
Find the number of pairs of indices $(l, r)$ ($1 \le l \le r \le n$) such that the value of median of $a_l, a_{l+1}, \dots, a_r$ is exactly the given number $m$.
The median of a sequence is the value of an element which is in the middle of the sequence after sorting it in non-decreasing order. If the length of the sequence is even, the left of two middle elements is used.
For example, if $a=[4, 2, 7, 5]$ then its median is $4$ since after sorting the sequence, it will look like $[2, 4, 5, 7]$ and the left of two middle elements is equal to $4$. The median of $[7, 1, 2, 9, 6]$ equals $6$ since after sorting, the value $6$ will be in the middle of the sequence.
Write a program to find the number of pairs of indices $(l, r)$ ($1 \le l \le r \le n$) such that the value of median of $a_l, a_{l+1}, \dots, a_r$ is exactly the given number $m$.
-----Input-----
The first line contains integers $n$ and $m$ ($1 \le n,m \le 2\cdot10^5$) — the length of the given sequence and the required value of the median.
The second line contains an integer sequence $a_1, a_2, \dots, a_n$ ($1 \le a_i \le 2\cdot10^5$).
-----Output-----
Print the required number.
-----Examples-----
Input
5 4
1 4 5 60 4
Output
8
Input
3 1
1 1 1
Output
6
Input
15 2
1 2 3 1 2 3 1 2 3 1 2 3 1 2 3
Output
97
-----Note-----
In the first example, the suitable pairs of indices are: $(1, 3)$, $(1, 4)$, $(1, 5)$, $(2, 2)$, $(2, 3)$, $(2, 5)$, $(4, 5)$ and $(5, 5)$.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [\"10\\n206158430208 206162624513 68719476737 137506062337 206162624513 4194305 68719476737 206225539072 137443147777 68719476736\\n202243898 470292528 170057449 290025540 127995253 514454151 607963029 768676450 611202521 68834463\\n\", \"2\\n0 1\\n1 1\\n\", \"10\\n3 3 5 5 6 6 1 2 4 7\\n1 1 1 1 1 1 1 1 1 1\\n\", \"2\\n0 0\\n69 6969\\n\", \"10\\n206158430208 206162624513 68719476737 137506062337 206162624513 4194305 68719476737 206225539072 137443147777 68719476736\\n202243898 470292528 170057449 290025540 16221286 514454151 607963029 768676450 611202521 68834463\\n\", \"2\\n0 1\\n1 2\\n\", \"2\\n0 0\\n61 6969\\n\", \"4\\n3 2 3 6\\n2 8 5 13\\n\", \"10\\n206158430208 206162624513 68719476737 137506062337 206162624513 4194305 68719476737 206225539072 137443147777 73922771262\\n202243898 470292528 170057449 290025540 16221286 514454151 607963029 768676450 611202521 68834463\\n\", \"2\\n0 0\\n46 6969\\n\", \"10\\n206158430208 206162624513 68719476737 137506062337 206162624513 4194305 68719476737 206225539072 137443147777 73922771262\\n202243898 470292528 170057449 290025540 16221286 514454151 607963029 768676450 153205637 68834463\\n\", \"2\\n0 0\\n46 6557\\n\", \"10\\n206158430208 206162624513 68719476737 114342791865 206162624513 4194305 68719476737 206225539072 129468784367 73922771262\\n202243898 470292528 170057449 290025540 16221286 514454151 607963029 768676450 153205637 68834463\\n\", \"2\\n0 0\\n44 6557\\n\", \"2\\n0 0\\n63 6557\\n\", \"2\\n0 0\\n63 7008\\n\", \"2\\n0 0\\n63 10792\\n\", \"10\\n206158430208 206162624513 68719476737 217758549476 206162624513 4194305 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 170057449 100548427 16221286 514454151 607963029 654940662 114059201 68834463\\n\", \"3\\n3 3 6\\n0 3 -2\\n\", \"3\\n1 2 6\\n1 2 3\\n\", \"1\\n1\\n1\\n\", \"2\\n0 1\\n1 0\\n\", \"3\\n1 2 6\\n1 2 0\\n\", \"1\\n2\\n1\\n\", \"2\\n0 1\\n2 0\\n\", \"3\\n1 2 6\\n2 2 0\\n\", \"1\\n2\\n2\\n\", \"10\\n206158430208 206162624513 68719476737 114342791865 206162624513 4194305 68719476737 206225539072 137443147777 73922771262\\n202243898 470292528 170057449 290025540 16221286 514454151 607963029 768676450 153205637 68834463\\n\", \"2\\n0 1\\n46 6557\\n\", \"3\\n1 3 6\\n2 2 0\\n\", \"1\\n2\\n0\\n\", \"3\\n1 3 6\\n0 2 0\\n\", \"1\\n3\\n0\\n\", \"10\\n206158430208 206162624513 68719476737 114342791865 206162624513 4194305 68719476737 206225539072 129468784367 73922771262\\n202243898 470292528 170057449 290025540 16221286 514454151 607963029 654940662 153205637 68834463\\n\", \"3\\n1 3 6\\n0 3 0\\n\", \"1\\n3\\n-1\\n\", \"10\\n206158430208 206162624513 68719476737 217758549476 206162624513 4194305 68719476737 206225539072 129468784367 73922771262\\n202243898 470292528 170057449 290025540 16221286 514454151 607963029 654940662 153205637 68834463\\n\", \"3\\n1 3 6\\n0 3 -1\\n\", \"1\\n2\\n-1\\n\", \"10\\n206158430208 206162624513 68719476737 217758549476 206162624513 4194305 68719476737 206225539072 129468784367 73922771262\\n202243898 470292528 170057449 290025540 16221286 514454151 607963029 654940662 114059201 68834463\\n\", \"3\\n1 3 6\\n0 3 -2\\n\", \"1\\n4\\n-1\\n\", \"10\\n206158430208 206162624513 68719476737 217758549476 206162624513 4194305 68719476737 206225539072 129468784367 73922771262\\n202243898 470292528 170057449 100548427 16221286 514454151 607963029 654940662 114059201 68834463\\n\", \"3\\n2 3 6\\n0 3 -2\\n\", \"1\\n5\\n-1\\n\", \"1\\n10\\n-1\\n\", \"10\\n206158430208 206162624513 68719476737 217758549476 108284112867 4194305 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 170057449 100548427 16221286 514454151 607963029 654940662 114059201 68834463\\n\", \"3\\n3 1 6\\n0 3 -2\\n\", \"1\\n12\\n-1\\n\", \"10\\n206158430208 206162624513 68719476737 217758549476 108284112867 4194305 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 100548427 16221286 514454151 607963029 654940662 114059201 68834463\\n\", \"3\\n2 1 6\\n0 3 -2\\n\", \"1\\n11\\n-1\\n\", \"10\\n206158430208 206162624513 68719476737 217758549476 108284112867 4194305 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 16221286 514454151 607963029 654940662 114059201 68834463\\n\", \"3\\n2 1 6\\n0 3 -3\\n\", \"1\\n11\\n0\\n\", \"10\\n206158430208 206162624513 68719476737 217758549476 108284112867 4194305 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 22413304 514454151 607963029 654940662 114059201 68834463\\n\", \"3\\n2 1 6\\n0 2 -3\\n\", \"1\\n11\\n1\\n\", \"10\\n206158430208 206162624513 68719476737 217758549476 108284112867 8112169 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 22413304 514454151 607963029 654940662 114059201 68834463\\n\", \"3\\n2 1 6\\n0 2 -6\\n\", \"1\\n5\\n1\\n\", \"10\\n206158430208 206162624513 68719476737 63960246561 108284112867 8112169 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 22413304 514454151 607963029 654940662 114059201 68834463\\n\", \"1\\n5\\n0\\n\", \"10\\n206158430208 206162624513 68719476737 63960246561 3746545026 8112169 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 22413304 514454151 607963029 654940662 114059201 68834463\\n\", \"1\\n4\\n0\\n\", \"10\\n206158430208 206162624513 74107770634 63960246561 3746545026 8112169 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 22413304 514454151 607963029 654940662 114059201 68834463\\n\", \"1\\n4\\n1\\n\", \"10\\n206158430208 206162624513 74107770634 63960246561 3746545026 8112169 10845574205 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 22413304 514454151 607963029 1209165361 114059201 68834463\\n\", \"1\\n3\\n1\\n\", \"10\\n206158430208 206162624513 74107770634 63960246561 3746545026 8112169 13383225525 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 22413304 514454151 607963029 1209165361 114059201 68834463\\n\", \"1\\n3\\n2\\n\", \"10\\n206158430208 206162624513 74107770634 63960246561 3746545026 8112169 13383225525 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 26295973 514454151 607963029 1209165361 114059201 68834463\\n\", \"1\\n4\\n2\\n\", \"10\\n206158430208 206162624513 74107770634 63960246561 3746545026 8112169 13383225525 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 26295973 514454151 607963029 2283944936 114059201 68834463\\n\", \"1\\n4\\n3\\n\", \"10\\n186947656767 206162624513 74107770634 63960246561 3746545026 8112169 13383225525 206225539072 129468784367 73922771262\\n202243898 470292528 205167640 69836668 26295973 514454151 607963029 2283944936 114059201 68834463\\n\", \"1\\n0\\n-1\\n\", \"10\\n186947656767 206162624513 74107770634 63960246561 3746545026 8112169 13383225525 206225539072 129468784367 73922771262\\n202243898 627954580 205167640 69836668 26295973 514454151 607963029 2283944936 114059201 68834463\\n\", \"1\\n0\\n0\\n\", \"3\\n1 2 3\\n1 2 3\\n\", \"1\\n0\\n1\\n\", \"4\\n3 2 3 6\\n2 8 5 10\\n\"], \"outputs\": [\"2773043292\\n\", \"0\\n\", \"9\\n\", \"7038\\n\", \"2661269325\\n\", \"0\\n\", \"7030\\n\", \"15\\n\", \"2592434862\\n\", \"7015\\n\", \"2134437978\\n\", \"6603\\n\", \"1981232341\\n\", \"6601\\n\", \"6620\\n\", \"7071\\n\", \"10855\\n\", \"1373269312\\n\", \"3\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"2134437978\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"1981232341\\n\", \"0\\n\", \"0\\n\", \"1981232341\\n\", \"0\\n\", \"0\\n\", \"1981232341\\n\", \"0\\n\", \"0\\n\", \"1981232341\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"15\\n\"]}", "source": "taco"}
|
Marcin is a coach in his university. There are n students who want to attend a training camp. Marcin is a smart coach, so he wants to send only the students that can work calmly with each other.
Let's focus on the students. They are indexed with integers from 1 to n. Each of them can be described with two integers a_i and b_i; b_i is equal to the skill level of the i-th student (the higher, the better). Also, there are 60 known algorithms, which are numbered with integers from 0 to 59. If the i-th student knows the j-th algorithm, then the j-th bit (2^j) is set in the binary representation of a_i. Otherwise, this bit is not set.
Student x thinks that he is better than student y if and only if x knows some algorithm which y doesn't know. Note that two students can think that they are better than each other. A group of students can work together calmly if no student in this group thinks that he is better than everyone else in this group.
Marcin wants to send a group of at least two students which will work together calmly and will have the maximum possible sum of the skill levels. What is this sum?
Input
The first line contains one integer n (1 ≤ n ≤ 7000) — the number of students interested in the camp.
The second line contains n integers. The i-th of them is a_i (0 ≤ a_i < 2^{60}).
The third line contains n integers. The i-th of them is b_i (1 ≤ b_i ≤ 10^9).
Output
Output one integer which denotes the maximum sum of b_i over the students in a group of students which can work together calmly. If no group of at least two students can work together calmly, print 0.
Examples
Input
4
3 2 3 6
2 8 5 10
Output
15
Input
3
1 2 3
1 2 3
Output
0
Input
1
0
1
Output
0
Note
In the first sample test, it's optimal to send the first, the second and the third student to the camp. It's also possible to send only the first and the third student, but they'd have a lower sum of b_i.
In the second test, in each group of at least two students someone will always think that he is better than everyone else in the subset.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"2\\n?rum??mer\\nc??a??mp\", \"3\\nsnuje\\n????e\\neluns\", \"2\\n?rum??mer\\nc@?a??mp\", \"3\\nsunje\\n????e\\neluns\", \"2\\n?rum??mer\\ncA?a??mp\", \"3\\nsunje\\n@???e\\neluns\", \"2\\nrem??mur?\\ncA?a??mp\", \"3\\nsunje\\n@???e\\nsnule\", \"2\\nsem??mur?\\ncA?a??mp\", \"3\\njunse\\n@???e\\nsnule\", \"2\\nsem??mur?\\ncA?a>?mp\", \"3\\nesnuj\\n@???e\\nsnule\", \"2\\nsem??mur?\\npm?>a?Ac\", \"3\\nesnuj\\n@?e??\\nsnule\", \"2\\nsem??mur?\\npm?>a?Ab\", \"3\\nesnuj\\n@?f??\\nsnule\", \"2\\n?rum??mes\\npm?>a?Ab\", \"3\\nesnuj\\n@?f??\\nnsule\", \"2\\nr?um??mes\\npm?>a?Ab\", \"3\\nesnuj\\n@???f\\nnsule\", \"2\\nr?um??mes\\npm?a>?Ab\", \"3\\nnseuj\\n@???f\\nnsule\", \"2\\nrmu???mes\\npm?a>?Ab\", \"3\\nnseuj\\n@???e\\nnsule\", \"2\\nrmu???les\\npm?a>?Ab\", \"3\\nnseuj\\n@???d\\nnsule\", \"2\\nrmu???les\\npm?a>@Ab\", \"3\\nnseuj\\n@???d\\nelusn\", \"2\\nrmu???les\\npm>a>@Ab\", \"3\\nnseuj\\n@???e\\nelusn\", \"2\\nrmul???es\\npm>a>@Ab\", \"3\\nnseuj\\n@>??e\\nelusn\", \"2\\nrmul???es\\npm>a>@Ac\", \"3\\nnteuj\\n@>??e\\nelusn\", \"2\\nrmul???es\\n@m>a>pAc\", \"3\\nntetj\\n@>??e\\nelusn\", \"2\\nrmul???es\\n@m>`>pAc\", \"3\\nntetj\\n@??>e\\nelusn\", \"2\\nr?ul??mes\\n@m>`>pAc\", \"3\\nnsetj\\n@??>e\\nelusn\", \"2\\nr?ul??mes\\n@m>`>pcA\", \"3\\nnsetj\\n@???e\\nelusn\", \"2\\nr?ul??les\\n@m>`>pcA\", \"3\\nnsesj\\n@???e\\nelusn\", \"2\\nr?ul??les\\n@c>`>pmA\", \"3\\nnsesj\\n@???e\\nemusn\", \"2\\n?rul??les\\n@c>`>pmA\", \"3\\nnsesi\\n@???e\\nemusn\", \"2\\n?rul??les\\nmc>`>p@A\", \"3\\nntesi\\n@???e\\nemusn\", \"2\\nsel??lur?\\nmc>`>p@A\", \"3\\nntesi\\ne???@\\nemusn\", \"2\\nsel??mur?\\nmc>`>p@A\", \"3\\nnsesi\\ne???@\\nemusn\", \"2\\nsel??mur?\\nA@p>`>cm\", \"3\\nnsesi\\ne???@\\nenusn\", \"2\\nsel??mur?\\nAcp>`>@m\", \"3\\nnsesi\\n@???e\\nenusn\", \"2\\nsel??mur?\\nAcp>`m@>\", \"3\\nnsesi\\n@?@?e\\nenusn\", \"2\\nsel??mur?\\n>@m`>pcA\", \"3\\nnsesi\\n@?@?e\\nnsune\", \"2\\ntel??mur?\\n>@m`>pcA\", \"3\\nnsesi\\n@?A?e\\nnsune\", \"2\\ntel??mur?\\n>@m`Apc>\", \"3\\nnsesi\\ne?A?@\\nnsune\", \"2\\ntel??mur?\\n>@maApc>\", \"3\\nnsesi\\n??Ae@\\nnsune\", \"2\\ntel??mur?\\n>@caApm>\", \"3\\nnsfsi\\n??Ae@\\nnsune\", \"2\\ntel??mur?\\n>@campA>\", \"3\\nnsfsi\\n??Ae@\\nnnuse\", \"2\\ntel??mur?\\n>@campB>\", \"3\\nnsfsi\\n>?Ae@\\nnnuse\", \"2\\n?rum??let\\n>@campB>\", \"3\\nssfni\\n>?Ae@\\nnnuse\", \"2\\n?rvm??let\\n>@campB>\", \"3\\ntsfni\\n>?Ae@\\nnnuse\", \"2\\n?rvm??lft\\n>@campB>\", \"3\\ntsfni\\n>?Ae@\\nneusn\", \"2\\ntfl??mvr?\\n>@campB>\", \"3\\ntsfni\\n>?Ae@\\nneusm\", \"2\\ntfl??mvs?\\n>@campB>\", \"3\\nssfni\\n>?Ae@\\nneusm\", \"2\\ntfl??mvs?\\n>@campB=\", \"3\\nssfni\\n>@Ae@\\nneusm\", \"2\\ntfm??mvs?\\n>@campB=\", \"3\\nssfni\\n@eA@>\\nneusm\", \"2\\ntfn??mvs?\\n>@campB=\", \"3\\nrsfni\\n@eA@>\\nneusm\", \"2\\ntfn??mvs?\\n>@calpB=\", \"3\\ninfsr\\n@eA@>\\nneusm\", \"2\\ntfn??mvs?\\n>pcal@B=\", \"3\\ninfsr\\n>eA@@\\nneusm\", \"2\\ntfn??mws?\\n>pcal@B=\", \"3\\ninfsr\\n@@Ae>\\nneusm\", \"2\\ntfn??mvs?\\n>Bcal@p=\", \"3\\ninrsf\\n@@Ae>\\nneusm\", \"2\\ntfn??mvs?\\n>cBal@p=\", \"3\\ninrsf\\n@@Ae>\\nmsuen\", \"2\\n?sum??mer\\nc??a??mp\", \"3\\nsnuje\\n????e\\nsnule\"], \"outputs\": [\"715167440\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"0\\n\", \"703286064\", \"1\"]}", "source": "taco"}
|
Sunuke-kun's dictionary contains the words s1, ..., sn, which consist of n lowercase letters. This satisfies s1 <... <sn when compared in lexicographical order. Unfortunately, some characters are faint and unreadable. Unreadable characters are represented by?. Find out how many ways to restore the dictionary by replacing? With lowercase letters, even with mod 1,000,000,007.
Constraints
* 1 ≤ n ≤ 50
* 1 ≤ | si | ≤ 20
* The characters that appear in si are lowercase letters or?
Input
n
s1
.. ..
sn
Output
Print the answer on one line.
Examples
Input
2
?sum??mer
c??a??mp
Output
703286064
Input
3
snuje
????e
snule
Output
1
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [\"3 2\\n1 2\\n2 3\\n1 2 1\\n\", \"4 2\\n1 2\\n3 4\\n1 2 3 3\\n\", \"1 0\\n1\\n\", \"2 1\\n2 1\\n2 2\\n\", \"2 1\\n2 1\\n1 2\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 1 3 2\\n\", \"4 3\\n4 3\\n3 2\\n2 1\\n3 4 4 4\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 1 1 2\\n\", \"1 0\\n1\\n\", \"4 3\\n4 3\\n3 2\\n2 1\\n3 4 4 4\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 1 1 2\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 1 3 2\\n\", \"2 1\\n2 1\\n1 2\\n\", \"2 1\\n2 1\\n2 2\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 1 1 4\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n2 1 1 2\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 1 3 3\\n\", \"3 2\\n1 2\\n2 3\\n1 2 2\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 2 3 3\\n\", \"4 2\\n1 2\\n3 4\\n1 1 3 3\\n\", \"3 2\\n1 2\\n2 3\\n1 1 1\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 1 3 4\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 2 3 4\\n\", \"4 3\\n4 3\\n3 2\\n2 1\\n3 4 4 2\\n\", \"4 3\\n1 2\\n2 3\\n2 4\\n1 1 1 4\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n3 1 1 2\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n3 2 1 2\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n2 1 3 2\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 2 3 2\\n\", \"4 3\\n1 2\\n1 3\\n3 4\\n1 1 3 3\\n\", \"4 3\\n1 2\\n1 3\\n2 4\\n1 1 1 4\\n\", \"4 3\\n4 3\\n3 2\\n2 1\\n3 4 4 3\\n\", \"4 3\\n1 2\\n1 3\\n3 4\\n1 1 3 1\\n\", \"3 2\\n1 2\\n1 3\\n1 2 1\\n\", \"4 3\\n1 2\\n1 3\\n1 4\\n1 1 1 4\\n\", \"4 3\\n1 2\\n2 3\\n3 4\\n1 1 1 1\\n\", \"4 3\\n1 2\\n4 3\\n2 4\\n1 1 1 4\\n\", \"4 3\\n1 2\\n4 3\\n2 4\\n2 1 1 4\\n\", \"4 3\\n1 2\\n2 3\\n1 4\\n1 1 1 1\\n\", \"3 2\\n1 2\\n1 3\\n1 1 1\\n\", \"4 3\\n1 2\\n4 3\\n2 4\\n1 1 2 4\\n\", \"3 2\\n1 2\\n2 3\\n1 2 1\\n\", \"4 2\\n1 2\\n3 4\\n1 2 3 3\\n\"], \"outputs\": [\"-1\", \"3\\n2\\n1\\n3\\n\", \"1\\n1\\n\", \"1\\n2\\n\", \"2\\n1\\n2\\n\", \"-1\", \"-1\", \"-1\", \"1\\n1\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"2\\n1\\n2\\n\", \"1\\n2\\n\", \"2\\n4\\n1\\n\", \"-1\\n\", \"2\\n3\\n1\\n\", \"2\\n2\\n1\\n\", \"3\\n3\\n2\\n1\\n\", \"2\\n1\\n3\\n\", \"1\\n1\\n\", \"3\\n4\\n3\\n1\\n\", \"4\\n4\\n3\\n2\\n1\\n\", \"-1\\n\", \"2\\n4\\n1\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"-1\\n\", \"2\\n3\\n1\\n\", \"2\\n4\\n1\\n\", \"-1\\n\", \"-1\\n\", \"2\\n2\\n1\\n\", \"2\\n4\\n1\\n\", \"1\\n1\\n\", \"-1\\n\", \"-1\\n\", \"1\\n1\\n\", \"1\\n1\\n\", \"-1\\n\", \"-1\\n\", \"3\\n2\\n1\\n3\\n\"]}", "source": "taco"}
|
Sasha lives in a big happy family. At the Man's Day all the men of the family gather to celebrate it following their own traditions. There are n men in Sasha's family, so let's number them with integers from 1 to n.
Each man has at most one father but may have arbitrary number of sons.
Man number A is considered to be the ancestor of the man number B if at least one of the following conditions is satisfied: A = B; the man number A is the father of the man number B; there is a man number C, such that the man number A is his ancestor and the man number C is the father of the man number B.
Of course, if the man number A is an ancestor of the man number B and A ≠ B, then the man number B is not an ancestor of the man number A.
The tradition of the Sasha's family is to give gifts at the Man's Day. Because giving gifts in a normal way is boring, each year the following happens. A list of candidates is prepared, containing some (possibly all) of the n men in some order. Each of the n men decides to give a gift. In order to choose a person to give a gift to, man A looks through the list and picks the first man B in the list, such that B is an ancestor of A and gives him a gift. Note that according to definition it may happen that a person gives a gift to himself. If there is no ancestor of a person in the list, he becomes sad and leaves the celebration without giving a gift to anyone.
This year you have decided to help in organizing celebration and asked each of the n men, who do they want to give presents to (this person is chosen only among ancestors). Are you able to make a list of candidates, such that all the wishes will be satisfied if they give gifts according to the process described above?
-----Input-----
In the first line of the input two integers n and m (0 ≤ m < n ≤ 100 000) are given — the number of the men in the Sasha's family and the number of family relations in it respectively.
The next m lines describe family relations: the (i + 1)^{th} line consists of pair of integers p_{i} and q_{i} (1 ≤ p_{i}, q_{i} ≤ n, p_{i} ≠ q_{i}) meaning that the man numbered p_{i} is the father of the man numbered q_{i}. It is guaranteed that every pair of numbers appears at most once, that among every pair of two different men at least one of them is not an ancestor of another and that every man has at most one father.
The next line contains n integers a_1, a_2, ..., a_{n} (1 ≤ a_{i} ≤ n), i^{th} of which means that the man numbered i wants to give a gift to the man numbered a_{i}. It is guaranteed that for every 1 ≤ i ≤ n the man numbered a_{i} is an ancestor of the man numbered i.
-----Output-----
Print an integer k (1 ≤ k ≤ n) — the number of the men in the list of candidates, in the first line.
Print then k pairwise different positive integers not exceeding n — the numbers of the men in the list in an order satisfying every of the men's wishes, one per line.
If there are more than one appropriate lists, print any of them. If there is no appropriate list print - 1 in the only line.
-----Examples-----
Input
3 2
1 2
2 3
1 2 1
Output
-1
Input
4 2
1 2
3 4
1 2 3 3
Output
3
2
1
3
-----Note-----
The first sample explanation: if there would be no 1 in the list then the first and the third man's wishes would not be satisfied (a_1 = a_3 = 1); if there would be no 2 in the list then the second man wish would not be satisfied (a_2 = 2); if 1 would stay before 2 in the answer then the second man would have to give his gift to the first man, but he wants to give it to himself (a_2 = 2). if, at the other hand, the man numbered 2 would stay before the man numbered 1, then the third man would have to give his gift to the second man, but not to the first (a_3 = 1).
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"445762753 268435456\\n\", \"144342486 67108864\\n\", \"257655784 16384\\n\", \"341001112 155173936\\n\", \"329622201 19482151\\n\", \"987654321987 1048576\\n\", \"58797441 33554432\\n\", \"4890852 16\\n\", \"70 32\\n\", \"163985731 33554432\\n\", \"9581849 1024\\n\", \"8670529 16384\\n\", \"35 4\\n\", \"62695452 33554432\\n\", \"175456797 16384\\n\", \"1000000000000 1000000000000\\n\", \"6 4\\n\", \"170427799 16\\n\", \"758646694 67108864\\n\", \"621597009 268435456\\n\", \"82 16\\n\", \"168544291 8\\n\", \"119581441 33554432\\n\", \"79 32\\n\", \"121749691 33554432\\n\", \"1000000000000 16\\n\", \"63 16\\n\", \"303397385 106697011\\n\", \"473038165 2\\n\", \"79375582 67108864\\n\", \"1000000000000 549755813888\\n\", \"138791611 67108864\\n\", \"326051437 4\\n\", \"1000000000 1000000001\\n\", \"47738179 16777216\\n\", \"543649338 175236010\\n\", \"112400107 67108864\\n\", \"585863386 33554432\\n\", \"82426873 1\\n\", \"304012333 67108864\\n\", \"445762753 156800291\\n\", \"165342893 67108864\\n\", \"233431959 16384\\n\", \"425523908799 1048576\\n\", \"134826378 33554432\\n\", \"6757729 16384\\n\", \"67 4\\n\", \"248089716 16384\\n\", \"218168575 16\\n\", \"447401851 67108864\\n\", \"82 8\\n\", \"209389925 33554432\\n\", \"113 16\\n\", \"82426873 2\\n\", \"1001000000000 1048576\\n\", \"4890852 1\\n\", \"168805380 33554432\\n\", \"34 4\\n\", \"341001112 97544362\\n\", \"329622201 35082096\\n\", \"42370378 33554432\\n\", \"4890852 5\\n\", \"35 32\\n\", \"62695452 28085892\\n\", \"1000000000000 1000000000100\\n\", \"6 7\\n\", \"621597009 204973018\\n\", \"168544291 6\\n\", \"119581441 47401930\\n\", \"79 46\\n\", \"1000000000000 30\\n\", \"358198368 106697011\\n\", \"473038165 3\\n\", \"79375582 65885288\\n\", \"1000000000000 68748452343\\n\", \"138791611 61847047\\n\", \"326051437 3\\n\", \"1000000000 1001000001\\n\", \"47738179 2762732\\n\", \"543649338 109383718\\n\", \"112400107 102385759\\n\", \"585863386 21908046\\n\", \"304012333 47684369\\n\", \"2 3\\n\", \"240060233 156800291\\n\", \"165342893 91912037\\n\", \"233431959 10478\\n\", \"341001112 31412867\\n\", \"473912944 35082096\\n\", \"425523908799 1557960\\n\", \"42370378 39239657\\n\", \"35 7\\n\", \"6757729 3674\\n\", \"85287837 28085892\\n\", \"1000000000000 1048576\\n\", \"3 3\\n\", \"1 1\\n\", \"3 2\\n\"], \"outputs\": [\"0\", \"1\", \"35969589\", \"0\", \"0\", \"116961880791\", \"0\", \"31009\", \"1\", \"27\", \"1563491\", \"493388\", \"11\", \"0\", \"22858807\", \"0\", \"1\", \"94897\", \"460\", \"1\", \"7\", \"20039\", \"3\", \"1\", \"3\", \"657969\", \"6\", \"0\", \"406\", \"0\", \"0\", \"1\", \"3601\", \"0\", \"1\", \"0\", \"0\", \"3655\", \"26\", \"28\", \"0\", \"1\", \"32064111\", \"46001789128\", \"27\", \"306124\", \"21\", \"34410180\", \"97824\", \"56\", \"20\", \"53\", \"15\", \"349\", \"118743657117\", \"22\", \"28\", \"11\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"118606527258\", \"0\", \"1\", \"1\"]}", "source": "taco"}
|
Maxim loves to fill in a matrix in a special manner. Here is a pseudocode of filling in a matrix of size (m + 1) × (m + 1):
<image>
Maxim asks you to count, how many numbers m (1 ≤ m ≤ n) are there, such that the sum of values in the cells in the row number m + 1 of the resulting matrix equals t.
Expression (x xor y) means applying the operation of bitwise excluding "OR" to numbers x and y. The given operation exists in all modern programming languages. For example, in languages C++ and Java it is represented by character "^", in Pascal — by "xor".
Input
A single line contains two integers n and t (1 ≤ n, t ≤ 1012, t ≤ n + 1).
Please, do not use the %lld specifier to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams or the %I64d specifier.
Output
In a single line print a single integer — the answer to the problem.
Examples
Input
1 1
Output
1
Input
3 2
Output
1
Input
3 3
Output
0
Input
1000000000000 1048576
Output
118606527258
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n0 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 4 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 1 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 8\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n0 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 4 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 8\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n0 3 1\\n1 1 3\\n0 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 4 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 1 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 1 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 2\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n1 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n0 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 2 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 4 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 1 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 4 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 1 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n1 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n0 4 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 2\\n0 3 1\\n0 4 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n1 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 2\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n1 1 2\\n5 5\\n0 2 2\\n1 1 5\\n0 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n0 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n0 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 4 3\\n0 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 2 3\\n1 3 1\\n0 2 3\\n1 2 4\\n6 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 1 1\\n1 1 5\\n1 5 4\\n0 5 2\\n0 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n0 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n0 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 1\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 2\\n0 3 1\\n0 4 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n1 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 4\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n1 1 2\\n5 5\\n0 2 2\\n1 1 5\\n0 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 3\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n0 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n0 4 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n0 1 2\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n5 5\\n1 1 2\\n0 1 3\\n1 3 1\\n0 2 3\\n1 2 4\\n8 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 5\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 1 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 3\\n2 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 1 4\\n4 5\\n1 3 1\\n1 1 3\\n0 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 2 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n0 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 1 1\\n0 2 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n2 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n2 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n0 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n0 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 2 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 4 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n2 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n0 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 3\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n0 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n0 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 4 1\\n0 2 3\\n1 2 1\\n4 5\\n1 4 1\\n1 1 3\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 1 3\\n1 3 1\\n0 2 3\\n1 2 4\\n6 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n2 3 5\\n4 5\\n1 1 2\\n0 1 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n0 2 5\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n0 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n0 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 2 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 4 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 4\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n0 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n0 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 1 4\\n1 3 2\\n\", \"4\\n3 1\\n0 2 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 4 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 4\\n0 1 4\\n1 2 4\\n0 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n0 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n0 2 4\\n4 4\\n1 4 1\\n1 1 3\\n0 1 2\\n1 1 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 3\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 1 3\\n1 3 1\\n0 2 3\\n1 2 4\\n8 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n5 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 4 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 2 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n2 1 1\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 4 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 1\\n2 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 1 2\\n1 1 5\\n1 5 4\\n0 5 2\\n0 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 1 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n1 4 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 4 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 1\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 1 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 3\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 3\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n1 5 2\\n1 2 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n5 5\\n1 3 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n0 4 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 2\\n0 1 4\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n5 5\\n1 1 2\\n0 1 3\\n1 3 1\\n0 2 3\\n1 2 4\\n8 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n1 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 2\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n6 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 1 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n1 1 2\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 3 1\\n1 1 3\\n1 1 1\\n1 2 4\\n2 3 2\\n\", \"4\\n3 1\\n0 1 2\\n9 5\\n0 2 2\\n1 1 5\\n1 5 4\\n0 5 2\\n1 2 9\\n4 5\\n1 1 2\\n0 4 3\\n0 3 1\\n0 4 3\\n1 2 4\\n7 5\\n1 3 1\\n1 1 3\\n1 1 3\\n1 2 4\\n1 3 2\\n\", \"4\\n3 1\\n0 1 3\\n5 5\\n0 2 1\\n1 1 5\\n1 5 4\\n0 5 2\\n1 3 5\\n4 5\\n1 1 2\\n0 4 3\\n1 3 1\\n0 2 3\\n1 2 4\\n4 5\\n1 4 1\\n1 1 3\\n0 1 2\\n1 2 4\\n1 3 2\\n\"], \"outputs\": [\"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n4 3\\n3 1\\n3 2\\n4 2\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nNO\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 1\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 8\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n2 5\\nNO\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 8\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nYES\\n1 3\\n1 3\\n1 1\\n2 4\\n3 2\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 4\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 1\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 1\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 2\\n3 2\\n2 4\\nNO\\n\", \"YES\\n1 2\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 2\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n2 5\\nNO\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 1\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n1 4\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 1\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nNO\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n1 4\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n2 4\\n3 1\\n3 4\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n1 2\\n1 5\\n5 4\\n5 2\\n3 5\\nYES\\n1 2\\n3 4\\n3 2\\n3 2\\n2 4\\nNO\\n\", \"YES\\n1 2\\nYES\\n2 2\\n1 5\\n4 5\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n4 3\\n3 1\\n4 3\\n4 2\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 2\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n1 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n4 3\\n3 1\\n3 2\\n4 2\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n4 3\\n3 1\\n3 2\\n4 2\\nNO\\n\", \"YES\\n1 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n2 4\\n3 1\\n3 4\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n1 2\\n1 5\\n5 4\\n5 2\\n3 5\\nYES\\n1 2\\n3 4\\n3 4\\n3 2\\n2 4\\nNO\\n\", \"YES\\n1 2\\nYES\\n2 2\\n1 5\\n4 5\\n2 5\\n2 5\\nNO\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n1 4\\n3 2\\n2 4\\nYES\\n4 1\\n2 1\\n4 1\\n2 4\\n3 2\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 1\\n3 1\\n3 2\\n2 4\\nYES\\n4 1\\n1 3\\n1 2\\n2 5\\n3 2\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 1\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n3 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n1 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n2 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n4 3\\n3 1\\n3 2\\n4 2\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n1 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 4\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n4 3\\n3 1\\n3 2\\n4 2\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nNO\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 1\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 1\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n4 3\\n3 1\\n3 2\\n4 2\\nNO\\n\", \"YES\\n3 2\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n2 5\\nNO\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n4 3\\n3 1\\n3 2\\n4 2\\nNO\\n\", \"YES\\n3 2\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n2 5\\nNO\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n4 3\\n3 1\\n3 2\\n4 2\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 1\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n2 5\\nNO\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 4\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 1\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n1 4\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 1\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nNO\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n1 4\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 1\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 2\\n3 2\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 1\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\", \"YES\\n2 1\\nYES\\n2 2\\n1 5\\n5 4\\n2 5\\n2 9\\nYES\\n1 2\\n3 4\\n3 1\\n3 4\\n2 4\\nNO\\n\", \"YES\\n3 1\\nYES\\n2 1\\n1 5\\n5 4\\n2 5\\n3 5\\nYES\\n1 2\\n3 4\\n3 1\\n3 2\\n2 4\\nNO\\n\"]}", "source": "taco"}
|
You are given a graph consisting of $n$ vertices and $m$ edges. It is not guaranteed that the given graph is connected. Some edges are already directed and you can't change their direction. Other edges are undirected and you have to choose some direction for all these edges.
You have to direct undirected edges in such a way that the resulting graph is directed and acyclic (i.e. the graph with all edges directed and having no directed cycles). Note that you have to direct all undirected edges.
You have to answer $t$ independent test cases.
-----Input-----
The first line of the input contains one integer $t$ ($1 \le t \le 2 \cdot 10^4$) — the number of test cases. Then $t$ test cases follow.
The first line of the test case contains two integers $n$ and $m$ ($2 \le n \le 2 \cdot 10^5$, $1 \le m \le min(2 \cdot 10^5, \frac{n(n-1)}{2})$) — the number of vertices and the number of edges in the graph, respectively.
The next $m$ lines describe edges of the graph. The $i$-th edge is described with three integers $t_i$, $x_i$ and $y_i$ ($t_i \in [0; 1]$, $1 \le x_i, y_i \le n$) — the type of the edge ($t_i = 0$ if the edge is undirected and $t_i = 1$ if the edge is directed) and vertices this edge connects (the undirected edge connects vertices $x_i$ and $y_i$ and directed edge is going from the vertex $x_i$ to the vertex $y_i$). It is guaranteed that the graph do not contain self-loops (i.e. edges from the vertex to itself) and multiple edges (i.e. for each pair ($x_i, y_i$) there are no other pairs ($x_i, y_i$) or ($y_i, x_i$)).
It is guaranteed that both sum $n$ and sum $m$ do not exceed $2 \cdot 10^5$ ($\sum n \le 2 \cdot 10^5$; $\sum m \le 2 \cdot 10^5$).
-----Output-----
For each test case print the answer — "NO" if it is impossible to direct undirected edges in such a way that the resulting graph is directed and acyclic, otherwise print "YES" on the first line and $m$ lines describing edges of the resulted directed acyclic graph (in any order). Note that you cannot change the direction of the already directed edges. If there are several answers, you can print any.
-----Example-----
Input
4
3 1
0 1 3
5 5
0 2 1
1 1 5
1 5 4
0 5 2
1 3 5
4 5
1 1 2
0 4 3
1 3 1
0 2 3
1 2 4
4 5
1 4 1
1 1 3
0 1 2
1 2 4
1 3 2
Output
YES
3 1
YES
2 1
1 5
5 4
2 5
3 5
YES
1 2
3 4
3 1
3 2
2 4
NO
-----Note-----
Explanation of the second test case of the example:
[Image]
Explanation of the third test case of the example:
[Image]
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[\"Too Easy?\"], [\"does\"], [\"your\"], [\"solution\"], [\"work\"], [\"for\"], [\"these\"], [\"words\"], [\"DOES\"], [\"YOUR\"], [\"SOLUTION\"], [\"WORK\"], [\"FOR\"], [\"THESE\"], [\"WORDS\"], [\"^does^\"], [\"$your$\"], [\"#solution#\"], [\"¿work¿\"], [\"{for}\"], [\"£these£\"], [\"?symbols?\"], [\"a\"], [\"aadvarks\"], [\"a/a/a/a/\"], [\"1234567890\"], [\"mississippi\"], [\"A\"], [\"AADVARKS\"], [\"A/A/A/A/\"], [\"MISSISSIPPI\"], [\"^\"], [\"^,@/_\"], [\"m¡$$¡$$¡pp¡\"], [\"abcde123fghij456klmno789pqrst.@0uvwxyz_/ \"], [\"ABCDE123FGHIJ456KLMNO789PQRST.@0UVWXYZ_/ \"], [\"^~?!'\\\"()-:;+&%*=<>€£$¥¤\\\\[]{},.@§#¿¡_/ \"], [\"Does\"], [\"Your\"], [\"Solution\"], [\"Work\"], [\"For\"], [\"These\"], [\"Words\"], [\"Xoo ooo ooo\"], [\"oXo ooo ooo\"], [\"ooX ooo ooo\"], [\"ooo Xoo ooo\"], [\"ooo oXo ooo\"], [\"ooo ooX ooo\"], [\"ooo ooo Xoo\"], [\"ooo ooo oXo\"], [\"ooo ooo ooX\"], [\"The Quick Brown Fox Jumps Over A Lazy Dog.\"], [\"Pack My Box With Five Dozen Liquor Jugs.\"], [\"\"], [\" \"], [\" \"], [\" x X \"]], \"outputs\": [[71], [16], [21], [33], [18], [12], [27], [23], [19], [22], [34], [19], [15], [28], [24], [33], [53], [49], [34], [38], [57], [54], [1], [30], [29], [26], [35], [4], [33], [32], [38], [5], [21], [54], [87], [90], [88], [29], [34], [46], [27], [21], [36], [32], [54], [66], [54], [54], [66], [54], [54], [66], [53], [262], [250], [0], [3], [5], [30]]}", "source": "taco"}
|
---
# Hint
This Kata is an extension of the earlier ones in this series. Completing those first will make this task easier.
# Background
My TV remote control has arrow buttons and an `OK` button.
I can use these to move a "cursor" on a logical screen keyboard to type words...
# Keyboard
The screen "keyboard" layouts look like this
#tvkb {
width : 400px;
border: 5px solid gray; border-collapse: collapse;
}
#tvkb td {
color : orange;
background-color : black;
text-align : center;
border: 3px solid gray; border-collapse: collapse;
}
#legend {
width : 400px;
border: 1px solid gray; border-collapse: collapse;
}
#legend td {
text-align : center;
border: 1px solid gray; border-collapse: collapse;
}
Keypad Mode 1 = alpha-numeric (lowercase)
Keypad Mode 3 = symbols
abcde123
fghij456
klmno789
pqrst.@0
uvwxyz_/
aA#SP
^~?!'"()
-:;+&%*=
<>€£$¥¤\
[]{},.@§
#¿¡_/
aA#SP
* `aA#` is the SHIFT key. Pressing this key cycles through THREE keypad modes.
* **Mode 1** = alpha-numeric keypad with lowercase alpha (as depicted above)
* **Mode 2** = alpha-numeric keypad with UPPERCASE alpha
* **Mode 3** = symbolic keypad (as depicted above)
* `SP` is the space character
* The other (solid fill) keys in the bottom row have no function
## Special Symbols
For your convenience, here are Unicode values for the less obvious symbols of the **Mode 3** keypad
¡ = U-00A1£ = U-00A3¤ = U-00A4¥ = U-00A5
§ = U-00A7¿ = U-00BF€ = U-20AC
# Kata task
How many button presses on my remote are required to type the given `words`?
## Notes
* The cursor always starts on the letter `a` (top left)
* The inital keypad layout is **Mode 1**
* Remember to also press `OK` to "accept" each letter
* Take the shortest route from one letter to the next
* The cursor wraps, so as it moves off one edge it will reappear on the opposite edge
* Although the blank keys have no function, you may navigate through them if you want to
* Spaces may occur anywhere in the `words` string
* Do not press the SHIFT key until you need to. For example, with the word `e.Z`, the SHIFT change happens **after** the `.` is pressed (not before). In other words, do not try to optimize total key presses by pressing SHIFT early.
```if:c,cpp
## C/C++ warriors
The standard I/O libraries choke on wide characters beyond the value 255. This kata includes the Euro € (U-20AC). So the function `ws2utf8()` has been preloaded for converting wchar_t strings to UTF-8 for printing.
```
# Example
words = `Too Easy?`
* T => `a`-`aA#`-OK-`U`-`V`-`W`-`X`-`Y`-`T`-OK = 9
* o => `T`-`Y`-`X`-`W`-`V`-`U`-`aA#`-OK-OK-`a`-`b`-`c`-`d`-`e`-`j`-`o`-OK = 16
* o => `o`-OK = 1
* space => `o`-`n`-`m`-`l`-`q`-`v`-`SP`-OK = 7
* E => `SP`-`aA#`-OK-`A`-`3`-`2`-`1`-`-E`-OK = 8
* a => `E`-`1`-`2`-`3`-`A`-`aA`-OK-OK-`a`-OK = 9
* s => `a`-`b`-`c`-`d`-`i`-`n`-`s`-OK = 7
* y => `s`-`x`-`y`-OK = 3
* ? => `y`-`x`-`w`-`v`-`u`-`aA#`-OK-OK-`^`-`~`-`?`-OK = 11
Answer = 9 + 16 + 1 + 7 + 8 + 9 + 7 + 3 + 11 = 71
*Good Luck!
DM.*
Series
* TV Remote
* TV Remote (shift and space)
* TV Remote (wrap)
* TV Remote (symbols)
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4\\n1 4 1\\n1 3 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n2 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 3 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 2 4\\n2 1 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n2 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 0 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 3 1\\n2 1 5\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n2 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 0 3\\n1 1 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n1 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 3 1\\n2 1 3\\n1 2 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 0 3\\n1 1 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 2 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n1 1 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 2\\n1 4 1\\n1 1 1\\n2 7 5\\n2 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 2 3\\n1 4 1\\n1 2 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 4 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 3\\n2 5 15\\n0 1 2\\n0\", \"4\\n1 4 2\\n1 3 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 2\\n2 5 15\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 4 2\\n1 2 4\\n2 4 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 3\\n2 5 15\\n0 1 2\\n0\", \"4\\n1 4 1\\n1 4 2\\n1 2 4\\n2 4 1\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 3\\n2 5 15\\n0 1 0\\n0\", \"4\\n1 4 2\\n1 4 2\\n1 2 4\\n2 4 1\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 3\\n2 5 15\\n0 1 0\\n0\", \"4\\n1 4 2\\n1 3 3\\n2 2 1\\n2 3 5\\n0\\n1 8 1\\n7\\n2 2 2\\n1 4 1\\n2 0 3\\n2 4 1\\n1 1 2\\n2 5 15\\n0 4 1\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 2 2\\n0\", \"4\\n1 4 1\\n2 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n2 2 4\\n2 3 5\\n1\\n1 3 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 8 5\\n1 4 2\\n0\", \"4\\n2 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 0 3\\n1 2 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 1 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 15\\n0 1 2\\n0\", \"4\\n1 4 1\\n1 1 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 2\\n2 5 15\\n0 1 2\\n0\", \"4\\n1 5 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n1 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n2 3 1\\n1 2 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 0 3\\n1 1 1\\n1 1 1\\n2 5 5\\n1 1 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n1 1 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 2\\n1 4 2\\n1 1 1\\n2 7 5\\n2 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n1 1 3\\n1 4 2\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n2 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 1 2\\n1 1 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n2 2 4\\n2 3 5\\n1\\n1 3 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 1\\n0\", \"4\\n2 5 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 0 3\\n1 2 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n1 1 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 2 2\\n1 4 2\\n1 1 1\\n2 7 5\\n2 4 2\\n0\", \"4\\n1 4 2\\n1 3 1\\n2 2 4\\n2 2 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n3 0 3\\n2 4 1\\n1 1 2\\n2 5 15\\n0 4 2\\n0\", \"4\\n1 2 2\\n1 3 1\\n2 2 4\\n2 3 5\\n0\\n2 12 1\\n14\\n2 2 2\\n1 4 1\\n2 0 3\\n2 4 1\\n1 1 2\\n2 5 15\\n0 4 1\\n0\", \"4\\n2 3 1\\n2 1 3\\n2 1 4\\n2 3 1\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 0\\n1 4 1\\n1 1 1\\n1 0 9\\n0 4 4\\n0\", \"4\\n1 2 1\\n2 0 1\\n1 2 3\\n2 3 5\\n0\\n1 2 0\\n7\\n2 2 5\\n1 3 1\\n2 1 3\\n1 0 1\\n1 2 1\\n2 4 9\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n1 2 4\\n2 4 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n2 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 0 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n2 2 4\\n2 3 5\\n1\\n2 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n2 4 1\\n1 2 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 3 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n2 2 4\\n2 4 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 3 1\\n2 1 3\\n1 2 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 0 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 0 3\\n1 1 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 0 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 2 2\\n0\", \"4\\n1 4 1\\n1 1 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 8 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 1 2\\n1 1 1\\n2 0 3\\n1 1 1\\n1 1 1\\n2 5 5\\n1 1 2\\n0\", \"4\\n2 5 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 0 3\\n1 1 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 1 2\\n2 2 4\\n2 3 5\\n1\\n1 3 1\\n7\\n2 2 4\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 1\\n0\", \"4\\n1 5 1\\n1 2 2\\n2 2 4\\n2 3 5\\n1\\n1 3 1\\n7\\n2 2 4\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 0 4\\n2 2 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 1\\n2 0 3\\n1 1 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n2 4 1\\n2 2 3\\n1 4 1\\n1 2 1\\n2 5 5\\n1 3 2\\n0\", \"4\\n2 4 1\\n1 3 2\\n1 1 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 2\\n1 1 2\\n1 1 1\\n2 7 5\\n2 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n2 4 4\\n2 3 5\\n1\\n1 3 1\\n7\\n2 2 2\\n1 4 1\\n1 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 1\\n0\", \"4\\n1 4 1\\n1 1 2\\n2 2 4\\n2 3 5\\n1\\n1 3 1\\n7\\n2 2 4\\n1 4 1\\n2 2 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 1\\n0\", \"4\\n1 4 1\\n1 2 1\\n1 2 3\\n2 3 5\\n0\\n1 5 2\\n2\\n2 0 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n3 0 16\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 7 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 2\\n1 4 1\\n1 1 1\\n2 7 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 3 1\\n2 1 5\\n1 4 1\\n1 1 1\\n2 5 0\\n1 4 2\\n0\", \"4\\n2 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 1 2\\n2 0 3\\n1 1 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 9\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 15\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 15\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 15\\n0 1 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 2\\n2 5 15\\n0 1 2\\n0\", \"4\\n2 4 1\\n1 2 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 4\\n1 3 1\\n2 1 5\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\", \"4\\n1 4 1\\n1 3 2\\n1 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 2\\n1 4 1\\n1 1 1\\n2 7 5\\n2 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 0 1\\n2 5 5\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 1\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 9\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 0 3\\n1 4 1\\n1 1 1\\n2 5 15\\n0 4 2\\n0\", \"4\\n1 4 2\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 15\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 15\\n0 1 0\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 3\\n2 5 15\\n0 1 2\\n0\", \"4\\n1 4 1\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n3 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 0 1\\n2 5 5\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 1\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n3 5 9\\n0 4 2\\n0\", \"4\\n1 4 2\\n1 2 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 2\\n2 5 15\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 1\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n3 0 9\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 2 1\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 0\\n1 4 1\\n1 1 1\\n3 0 9\\n0 4 2\\n0\", \"4\\n1 4 2\\n1 3 2\\n1 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 0 3\\n1 4 1\\n1 1 2\\n2 5 15\\n0 4 2\\n0\", \"4\\n1 4 1\\n1 4 2\\n1 2 4\\n2 4 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 3\\n2 5 15\\n0 1 0\\n0\", \"4\\n2 4 1\\n1 2 1\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 0\\n1 4 1\\n1 1 1\\n3 0 9\\n0 4 2\\n0\", \"4\\n1 4 2\\n1 3 2\\n2 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 0 3\\n1 4 1\\n1 1 2\\n2 5 15\\n0 4 2\\n0\", \"4\\n2 4 1\\n1 2 1\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 0\\n1 4 1\\n1 1 1\\n3 0 9\\n0 4 4\\n0\", \"4\\n1 4 2\\n1 3 2\\n2 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 0 3\\n2 4 1\\n1 1 2\\n2 5 15\\n0 4 2\\n0\", \"4\\n2 4 1\\n2 2 1\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 0\\n1 4 1\\n1 1 1\\n3 0 9\\n0 4 4\\n0\", \"4\\n1 4 2\\n1 3 2\\n2 2 4\\n2 3 5\\n0\\n1 6 1\\n7\\n2 2 2\\n1 4 1\\n2 0 3\\n2 4 1\\n1 1 2\\n2 5 15\\n0 4 1\\n0\", \"4\\n2 4 1\\n2 2 1\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n4 1 0\\n1 4 1\\n1 1 1\\n3 0 9\\n0 4 4\\n0\", \"4\\n1 4 2\\n1 3 2\\n2 2 4\\n2 3 5\\n0\\n1 8 1\\n7\\n2 2 2\\n1 4 1\\n2 0 3\\n2 4 1\\n1 1 2\\n2 5 15\\n0 4 1\\n0\", \"4\\n2 4 1\\n2 2 2\\n1 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n4 1 0\\n1 4 1\\n1 1 1\\n3 0 9\\n0 4 4\\n0\", \"4\\n1 4 2\\n1 3 3\\n2 2 4\\n2 3 5\\n0\\n1 8 1\\n7\\n2 2 2\\n1 4 1\\n2 0 3\\n2 4 1\\n1 1 2\\n2 5 15\\n0 4 1\\n0\", \"4\\n2 4 1\\n2 2 2\\n2 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n4 1 0\\n1 4 1\\n1 1 1\\n3 0 9\\n0 4 4\\n0\", \"4\\n2 4 1\\n2 2 2\\n2 2 4\\n2 3 5\\n0\\n1 5 1\\n7\\n4 2 2\\n1 4 1\\n4 1 0\\n1 4 1\\n1 1 1\\n3 0 9\\n0 4 4\\n0\", \"4\\n1 4 1\\n1 3 1\\n2 2 4\\n2 3 5\\n1\\n1 5 1\\n7\\n2 2 2\\n1 4 1\\n2 1 3\\n1 4 1\\n1 1 1\\n2 5 5\\n1 4 2\\n0\"], \"outputs\": [\"7\\n0\\n6\\n\", \"12\\n0\\n6\\n\", \"2\\n0\\n13\\n\", \"12\\n0\\n13\\n\", \"6\\n0\\n6\\n\", \"7\\n0\\n10\\n\", \"5\\n0\\n13\\n\", \"12\\n0\\n12\\n\", \"11\\n0\\n6\\n\", \"7\\n0\\n15\\n\", \"12\\n0\\n14\\n\", \"11\\n\", \"2\\n0\\n6\\n\", \"7\\n0\\n18\\n\", \"2\\n0\\n14\\n\", \"11\\n0\\n12\\n\", \"6\\n0\\n13\\n\", \"11\\n0\\n18\\n\", \"13\\n\", \"12\\n\", \"14\\n\", \"9\\n\", \"4\\n\", \"7\\n\", \"2\\n0\\n9\\n\", \"7\\n0\\n13\\n\", \"6\\n3\\n6\\n\", \"11\\n0\\n14\\n\", \"12\\n0\\n15\\n\", \"3\\n\", \"10\\n\", \"3\\n0\\n6\\n\", \"5\\n0\\n6\\n\", \"2\\n0\\n11\\n\", \"6\\n0\\n23\\n\", \"12\\n0\\n21\\n\", \"7\\n0\\n12\\n\", \"6\\n3\\n11\\n\", \"13\\n0\\n15\\n\", \"6\\n0\\n24\\n\", \"6\\n\", \"5\\n\", \"8\\n\", \"2\\n\", \"13\\n0\\n6\\n\", \"12\\n0\\n8\\n\", \"6\\n5\\n6\\n\", \"6\\n0\\n10\\n\", \"8\\n0\\n18\\n\", \"5\\n0\\n14\\n\", \"5\\n0\\n9\\n\", \"10\\n0\\n14\\n\", \"2\\n0\\n10\\n\", \"13\\n0\\n14\\n\", \"5\\n3\\n11\\n\", \"7\\n3\\n6\\n\", \"4\\n0\\n14\\n\", \"11\\n0\\n17\\n\", \"6\\n0\\n15\\n\", \"8\\n3\\n11\\n\", \"5\\n3\\n17\\n\", \"1\\n\", \"12\\n0\\n13\\n\", \"12\\n0\\n13\\n\", \"7\\n0\\n15\\n\", \"12\\n0\\n14\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"6\\n0\\n6\\n\", \"7\\n0\\n10\\n\", \"12\\n0\\n13\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"11\\n\", \"12\\n\", \"14\\n\", \"11\\n\", \"12\\n\", \"11\\n\", \"12\\n\", \"11\\n\", \"12\\n\", \"11\\n\", \"12\\n\", \"11\\n\", \"12\\n\", \"11\\n\", \"11\\n\", \"2\\n0\\n6\"]}", "source": "taco"}
|
Tetris is a game in which falling blocks are lined up on the board and erased. Here, let's consider a game that arranges it a little.
The size of the board of this game is 5 frames wide, and it is high enough to accommodate all the blocks that appear. The falling blocks are straight and come in two types, landscape and portrait, with five lengths from 1 to 5.
An example is shown below. The figure from Step (a) to Step (e) shows how the blocks fall and disappear. From Step (a), proceed in order of Step (b) and Step (c).
When dropping a block, if somewhere in the block is caught in a block piled up like Step (a), the dropped block like Step (b) will stop at that place. Also, as a result of dropping a block, if all the frames in a horizontal line on the board are clogged with blocks, the blocks in that line will disappear as shown in Step (d). After this, the block above the disappeared line will move down one line as it is (Step (e)).
<image>
In one game, up to 1000 blocks will be dropped in order. For example, the lengths of the falling blocks are 4 frames horizontally, 3 frames horizontally, 2 frames vertically, and 3 frames vertically, and the falling locations are the 1st, 1st, 4th, and 5th frames from the left end. If there is, it will drop as shown in Step (a) to (g) in the figure below, and the last remaining block will be 2 frames.
<image>
Create a program that inputs the information of the blocks that fall in order and outputs the number of frames remaining when all the blocks fall.
Input
A sequence of multiple datasets is given as input. The end of the input is indicated by a single line of zeros. Each dataset is given in the following format:
n
d1 p1 q1
d2 p2 q2
::
dn pn qn
The number of blocks n (1 ≤ n ≤ 1000) is given on the first line. The next n lines give the i-th block orientation di (1 or 2), the block length pi (1 ≤ pi ≤ 5), and the block position qi. Block orientation di is 1 for landscape orientation and 2 for portrait orientation. The block position qi is an integer from 1 to 5 from the left edge on the board, and in the case of a horizontal block, it is the position where the left edge frame falls.
The number of datasets does not exceed 20.
Output
The number of frames occupied by the last remaining block for each data set is output on one line.
Example
Input
4
1 4 1
1 3 1
2 2 4
2 3 5
1
1 5 1
7
2 2 2
1 4 1
2 1 3
1 4 1
1 1 1
2 5 5
1 4 2
0
Output
2
0
6
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"5 2 3\\n1 -1 1 -1 2\\n\", \"6 3 2\\n1 1 -1 -1 -1 -1\\n\", \"10 42 7\\n-1 -1 -1 -1 -1 -1 -1 -1 -1 -1\\n\", \"1 100 1\\n-1\\n\", \"1 100 1\\n-1\\n\", \"1 100 2\\n-1\\n\", \"6 3 2\\n1 1 -1 -1 0 -1\\n\", \"5 2 3\\n2 -1 1 -1 2\\n\", \"5 2 3\\n2 -1 2 -1 2\\n\", \"6 3 4\\n1 1 -1 -1 1 -1\\n\", \"6 3 2\\n1 2 -1 -1 -1 -1\\n\", \"10 32 7\\n-1 -1 -1 -1 -1 -1 -1 -1 -1 -1\\n\", \"1 010 4\\n-1\\n\", \"5 4 5\\n2 -1 2 -1 2\\n\", \"6 3 2\\n-1 1 -1 -1 -1 -1\\n\", \"5 6 5\\n2 -1 2 -1 3\\n\", \"5 5 5\\n2 -1 2 -1 3\\n\", \"5 5 3\\n2 -1 2 -1 3\\n\", \"6 3 4\\n1 1 -1 -1 1 1\\n\", \"1 100 4\\n-1\\n\", \"6 3 2\\n1 1 -1 -1 1 -1\\n\", \"6 3 2\\n1 1 -1 -1 0 0\\n\", \"6 3 2\\n1 1 -1 -1 1 0\\n\", \"5 2 1\\n2 -1 1 -1 2\\n\", \"5 2 2\\n2 -1 1 -1 2\\n\", \"1 000 2\\n-1\\n\", \"1 000 4\\n-1\\n\", \"5 2 5\\n2 -1 2 -1 2\\n\", \"5 2 1\\n0 -1 1 -1 2\\n\", \"5 2 1\\n0 -1 1 -2 2\\n\", \"5 4 5\\n2 -1 2 -1 4\\n\", \"5 4 1\\n0 -1 1 -2 2\\n\", \"6 3 2\\n1 1 -1 -1 0 1\\n\", \"6 3 2\\n1 1 -1 -1 1 1\\n\", \"1 010 2\\n-1\\n\", \"1 000 8\\n-1\\n\", \"5 5 5\\n2 -1 2 -1 2\\n\", \"5 2 1\\n0 0 1 -1 2\\n\", \"5 4 5\\n2 -1 2 -1 3\\n\", \"5 4 1\\n0 -1 1 -2 1\\n\", \"5 4 3\\n2 -1 1 -1 2\\n\", \"6 3 2\\n1 3 -1 -1 -1 -1\\n\", \"5 3 1\\n2 -1 1 -1 2\\n\", \"10 32 1\\n-1 -1 -1 -1 -1 -1 -1 -1 -1 -1\\n\", \"1 010 8\\n-1\\n\", \"5 2 1\\n0 -2 1 -1 2\\n\", \"5 2 1\\n0 -1 1 -4 2\\n\", \"5 4 1\\n0 -1 1 -2 3\\n\", \"6 3 1\\n-1 1 -1 -1 -1 -1\\n\", \"6 5 2\\n1 1 -1 -1 0 1\\n\", \"5 2 1\\n0 0 1 -2 2\\n\", \"5 4 7\\n2 -1 2 -1 3\\n\", \"5 4 1\\n0 -1 2 -2 1\\n\", \"5 6 5\\n2 -1 2 -1 1\\n\", \"5 5 5\\n2 -1 3 -1 3\\n\", \"6 3 2\\n1 1 -1 -1 -1 -1\\n\", \"5 2 3\\n1 -1 1 -1 2\\n\", \"10 42 7\\n-1 -1 -1 -1 -1 -1 -1 -1 -1 -1\\n\"], \"outputs\": [\"2\\n\", \"0\\n\", \"645711643\\n\", \"0\\n\", \"0\\n\", \"100\", \"0\", \"3\", \"1\", \"24\", \"16\", \"61884984\", \"10\", \"15\", \"32\", \"36\", \"25\", \"20\", \"8\", \"100\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"3\", \"0\", \"0\", \"16\", \"0\", \"0\", \"0\", \"10\", \"0\", \"24\", \"0\", \"16\", \"0\", \"15\", \"16\", \"0\", \"0\", \"10\", \"0\", \"0\", \"0\", \"0\", \"0\", \"0\", \"16\", \"0\", \"36\", \"25\", \"0\\n\", \"2\\n\", \"645711643\\n\"]}", "source": "taco"}
|
Vasya has got an array consisting of $n$ integers, and two integers $k$ and $len$ in addition. All numbers in the array are either between $1$ and $k$ (inclusive), or equal to $-1$. The array is good if there is no segment of $len$ consecutive equal numbers.
Vasya will replace each $-1$ with some number from $1$ to $k$ (inclusive) in such a way that the resulting array is good. Tell him the number of ways to do this replacement. Since the answer may be large, print it modulo $998244353$.
-----Input-----
The first line contains three integers $n, k$ and $len$ ($1 \le n \le 10^5, 1 \le k \le 100, 1 \le len \le n$).
The second line contains $n$ numbers — the array. Each number is either $-1$ or between $1$ and $k$ (inclusive).
-----Output-----
Print one integer — the number of ways to replace each $-1$ with some number from $1$ to $k$ (inclusive) so the array is good. The answer may be large, so print it modulo $998244353$.
-----Examples-----
Input
5 2 3
1 -1 1 -1 2
Output
2
Input
6 3 2
1 1 -1 -1 -1 -1
Output
0
Input
10 42 7
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1
Output
645711643
-----Note-----
Possible answers in the first test: $[1, 2, 1, 1, 2]$; $[1, 2, 1, 2, 2]$.
There is no way to make the array good in the second test, since first two elements are equal.
There are too many answers in the third test, so we won't describe any of them.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [\"4\\n1 0\\n2 2\\n0 2\\n0 1\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n4 2\\n1 3\\n3 3\", \"4\\n1 0\\n3 2\\n0 2\\n0 1\", \"7\\n4 1\\n0 0\\n1 2\\n2 0\\n4 2\\n1 3\\n3 3\", \"7\\n4 1\\n0 0\\n1 2\\n3 0\\n4 2\\n1 3\\n3 3\", \"7\\n2 1\\n0 0\\n1 2\\n2 2\\n4 2\\n1 3\\n0 3\", \"4\\n1 0\\n2 2\\n1 2\\n0 1\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n4 2\\n1 3\\n5 3\", \"4\\n1 1\\n3 2\\n0 2\\n0 1\", \"7\\n4 1\\n0 0\\n1 2\\n2 0\\n4 2\\n1 3\\n2 3\", \"7\\n4 1\\n0 0\\n0 2\\n3 0\\n4 2\\n1 3\\n3 3\", \"4\\n2 0\\n2 2\\n1 2\\n0 1\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n4 2\\n1 3\\n5 1\", \"4\\n1 1\\n3 0\\n0 2\\n0 1\", \"7\\n4 1\\n0 -1\\n1 2\\n2 0\\n4 2\\n1 3\\n2 3\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n2 2\\n1 3\\n5 1\", \"4\\n1 1\\n3 1\\n0 2\\n0 1\", \"7\\n4 1\\n0 -1\\n1 2\\n2 -1\\n4 2\\n1 3\\n2 3\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n3 2\\n1 3\\n5 1\", \"4\\n2 1\\n3 1\\n0 2\\n0 1\", \"7\\n4 1\\n0 -1\\n1 2\\n2 -2\\n4 2\\n1 3\\n2 3\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n3 2\\n1 3\\n9 1\", \"7\\n4 1\\n0 -1\\n1 2\\n2 -2\\n4 2\\n0 3\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n4 2\\n0 3\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n4 2\\n0 0\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 2\\n0 0\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 2\\n0 0\\n1 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 2\\n-1 0\\n1 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 2\\n-1 0\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 2\\n-1 -1\\n2 3\", \"4\\n0 0\\n2 2\\n1 2\\n0 1\", \"7\\n2 1\\n0 0\\n1 0\\n2 0\\n4 2\\n1 3\\n3 3\", \"4\\n1 -1\\n3 2\\n0 2\\n0 1\", \"7\\n4 1\\n0 0\\n1 2\\n2 0\\n4 2\\n1 3\\n3 4\", \"7\\n4 1\\n0 0\\n1 4\\n3 0\\n4 2\\n1 3\\n3 3\", \"7\\n2 1\\n0 0\\n1 2\\n2 2\\n4 2\\n1 1\\n0 3\", \"4\\n1 0\\n2 2\\n1 2\\n-1 1\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n4 2\\n1 3\\n2 3\", \"7\\n4 1\\n0 0\\n0 2\\n3 0\\n2 2\\n1 3\\n3 3\", \"4\\n2 -1\\n2 2\\n1 2\\n0 1\", \"7\\n4 1\\n0 -1\\n1 2\\n2 0\\n4 2\\n0 3\\n2 3\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n2 2\\n1 3\\n5 0\", \"4\\n1 1\\n3 1\\n-1 2\\n0 1\", \"7\\n4 1\\n0 -2\\n1 2\\n2 -1\\n4 2\\n1 3\\n2 3\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n3 2\\n1 4\\n5 1\", \"4\\n2 1\\n4 1\\n0 2\\n0 1\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n3 2\\n1 3\\n16 1\", \"7\\n4 1\\n0 -1\\n1 2\\n2 -2\\n4 2\\n-1 3\\n2 3\", \"7\\n2 2\\n0 0\\n1 2\\n0 1\\n3 2\\n1 3\\n9 1\", \"7\\n4 0\\n-1 -1\\n1 2\\n2 -2\\n4 2\\n0 3\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 0\\n4 2\\n0 0\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 1\\n0 0\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 2\\n0 0\\n1 6\", \"7\\n4 0\\n0 0\\n1 2\\n2 -2\\n7 2\\n-1 0\\n1 3\", \"7\\n4 0\\n0 -1\\n1 0\\n2 -2\\n7 2\\n-1 0\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 1\\n-1 -1\\n2 3\", \"4\\n0 0\\n2 3\\n1 2\\n0 1\", \"7\\n2 1\\n0 0\\n1 0\\n2 0\\n4 2\\n1 6\\n3 3\", \"4\\n1 -1\\n4 2\\n0 2\\n0 1\", \"7\\n4 1\\n0 0\\n1 2\\n2 0\\n4 2\\n1 3\\n0 4\", \"7\\n4 1\\n0 1\\n1 4\\n3 0\\n4 2\\n1 3\\n3 3\", \"7\\n2 1\\n0 0\\n1 2\\n2 2\\n4 0\\n1 1\\n0 3\", \"4\\n2 0\\n2 2\\n1 2\\n-1 1\", \"7\\n4 1\\n0 0\\n0 2\\n3 0\\n2 2\\n1 3\\n3 6\", \"4\\n2 -1\\n2 2\\n1 0\\n0 1\", \"7\\n4 1\\n0 -1\\n1 2\\n2 0\\n4 2\\n0 3\\n2 5\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n2 2\\n1 3\\n6 0\", \"4\\n1 1\\n3 2\\n-1 2\\n0 1\", \"7\\n4 1\\n0 -2\\n1 2\\n0 -1\\n4 2\\n1 3\\n2 3\", \"7\\n2 1\\n0 0\\n1 0\\n2 0\\n3 2\\n1 4\\n5 1\", \"4\\n2 1\\n4 1\\n-1 2\\n0 1\", \"7\\n8 1\\n0 -1\\n1 1\\n2 -2\\n4 2\\n1 3\\n2 3\", \"7\\n2 1\\n0 0\\n1 2\\n2 0\\n3 2\\n1 3\\n25 1\", \"7\\n4 1\\n0 -1\\n1 2\\n2 -2\\n4 2\\n-1 2\\n2 3\", \"7\\n2 2\\n0 0\\n1 2\\n0 1\\n3 2\\n1 3\\n16 1\", \"7\\n4 0\\n-1 -1\\n1 2\\n2 -3\\n4 2\\n0 3\\n2 3\", \"7\\n4 0\\n0 -1\\n1 2\\n2 0\\n4 2\\n0 0\\n2 4\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 1\\n0 0\\n2 0\", \"7\\n4 0\\n0 -1\\n1 2\\n1 -2\\n7 2\\n0 0\\n1 6\", \"7\\n4 0\\n0 0\\n0 2\\n2 -2\\n7 2\\n-1 0\\n1 3\", \"7\\n4 0\\n0 -1\\n1 0\\n2 -2\\n7 2\\n-1 1\\n2 3\", \"4\\n0 0\\n2 3\\n0 2\\n0 1\", \"7\\n2 1\\n0 0\\n1 0\\n2 0\\n4 2\\n1 12\\n3 3\", \"4\\n1 -2\\n4 2\\n0 2\\n0 1\", \"7\\n4 1\\n0 0\\n1 2\\n2 1\\n4 2\\n1 3\\n0 4\", \"7\\n2 1\\n0 -1\\n1 2\\n2 2\\n4 0\\n1 1\\n0 3\", \"4\\n2 0\\n2 2\\n1 1\\n-1 1\", \"7\\n4 1\\n0 0\\n0 2\\n3 0\\n4 2\\n1 3\\n3 6\", \"4\\n0 -1\\n2 2\\n1 0\\n0 1\", \"7\\n4 1\\n-1 -1\\n1 2\\n2 0\\n4 2\\n0 3\\n2 5\", \"4\\n1 1\\n4 2\\n-1 2\\n0 1\", \"7\\n2 1\\n0 0\\n1 0\\n2 0\\n3 0\\n1 4\\n5 1\", \"4\\n2 0\\n4 1\\n-1 2\\n0 1\", \"7\\n8 1\\n0 -1\\n1 1\\n2 -2\\n4 3\\n1 3\\n2 3\", \"7\\n4 1\\n0 -1\\n1 2\\n2 -2\\n4 2\\n-1 2\\n1 3\", \"7\\n2 2\\n0 0\\n1 2\\n0 1\\n3 2\\n1 3\\n18 1\", \"7\\n4 0\\n-1 -1\\n1 2\\n2 -3\\n4 2\\n0 3\\n2 2\", \"7\\n4 0\\n0 -1\\n1 2\\n2 -2\\n7 1\\n1 0\\n2 0\", \"7\\n4 0\\n0 -1\\n1 2\\n1 -2\\n7 2\\n0 1\\n1 6\", \"7\\n4 0\\n0 -1\\n1 0\\n2 -2\\n7 2\\n-1 1\\n0 3\", \"4\\n0 0\\n2 2\\n0 2\\n0 1\", \"7\\n2 1\\n0 0\\n1 2\\n2 2\\n4 2\\n1 3\\n3 3\"], \"outputs\": [\"4\\n1 0\\n2 2\\n0 2\\n0 1\\n\", \"5\\n0 0\\n2 0\\n4 2\\n3 3\\n1 3\\n\", \"4\\n1 0\\n3 2\\n0 2\\n0 1\\n\", \"6\\n0 0\\n2 0\\n4 1\\n4 2\\n3 3\\n1 3\\n\", \"6\\n0 0\\n3 0\\n4 1\\n4 2\\n3 3\\n1 3\\n\", \"5\\n0 0\\n2 1\\n4 2\\n1 3\\n0 3\\n\", \"4\\n1 0\\n2 2\\n1 2\\n0 1\\n\", \"5\\n0 0\\n2 0\\n4 2\\n5 3\\n1 3\\n\", \"4\\n0 1\\n1 1\\n3 2\\n0 2\\n\", \"6\\n0 0\\n2 0\\n4 1\\n4 2\\n2 3\\n1 3\\n\", \"7\\n0 0\\n3 0\\n4 1\\n4 2\\n3 3\\n1 3\\n0 2\\n\", \"4\\n2 0\\n2 2\\n1 2\\n0 1\\n\", \"5\\n0 0\\n2 0\\n5 1\\n4 2\\n1 3\\n\", \"3\\n3 0\\n0 2\\n0 1\\n\", \"6\\n0 -1\\n2 0\\n4 1\\n4 2\\n2 3\\n1 3\\n\", \"4\\n0 0\\n2 0\\n5 1\\n1 3\\n\", \"4\\n0 1\\n1 1\\n3 1\\n0 2\\n\", \"6\\n0 -1\\n2 -1\\n4 1\\n4 2\\n2 3\\n1 3\\n\", \"5\\n0 0\\n2 0\\n5 1\\n3 2\\n1 3\\n\", \"4\\n0 1\\n2 1\\n3 1\\n0 2\\n\", \"6\\n2 -2\\n4 1\\n4 2\\n2 3\\n1 3\\n0 -1\\n\", \"4\\n0 0\\n2 0\\n9 1\\n1 3\\n\", \"6\\n2 -2\\n4 1\\n4 2\\n2 3\\n0 3\\n0 -1\\n\", \"6\\n2 -2\\n4 0\\n4 2\\n2 3\\n0 3\\n0 -1\\n\", \"7\\n2 -2\\n4 0\\n4 2\\n2 3\\n1 2\\n0 0\\n0 -1\\n\", \"6\\n2 -2\\n7 2\\n2 3\\n1 2\\n0 0\\n0 -1\\n\", \"5\\n2 -2\\n7 2\\n1 3\\n0 0\\n0 -1\\n\", \"5\\n2 -2\\n7 2\\n1 3\\n-1 0\\n0 -1\\n\", \"6\\n2 -2\\n7 2\\n2 3\\n1 2\\n-1 0\\n0 -1\\n\", \"5\\n2 -2\\n7 2\\n2 3\\n1 2\\n-1 -1\\n\", \"4\\n0 0\\n2 2\\n1 2\\n0 1\\n\", \"6\\n0 0\\n1 0\\n2 0\\n4 2\\n3 3\\n1 3\\n\", \"4\\n1 -1\\n3 2\\n0 2\\n0 1\\n\", \"6\\n0 0\\n2 0\\n4 1\\n4 2\\n3 4\\n1 3\\n\", \"6\\n0 0\\n3 0\\n4 1\\n4 2\\n3 3\\n1 4\\n\", \"4\\n0 0\\n2 1\\n4 2\\n0 3\\n\", \"4\\n1 0\\n2 2\\n1 2\\n-1 1\\n\", \"5\\n0 0\\n2 0\\n4 2\\n2 3\\n1 3\\n\", \"6\\n0 0\\n3 0\\n4 1\\n3 3\\n1 3\\n0 2\\n\", \"4\\n2 -1\\n2 2\\n1 2\\n0 1\\n\", \"6\\n0 -1\\n2 0\\n4 1\\n4 2\\n2 3\\n0 3\\n\", \"4\\n0 0\\n2 0\\n5 0\\n1 3\\n\", \"4\\n0 1\\n1 1\\n3 1\\n-1 2\\n\", \"6\\n0 -2\\n2 -1\\n4 1\\n4 2\\n2 3\\n1 3\\n\", \"4\\n0 0\\n2 0\\n5 1\\n1 4\\n\", \"4\\n0 1\\n2 1\\n4 1\\n0 2\\n\", \"4\\n0 0\\n2 0\\n16 1\\n1 3\\n\", \"6\\n2 -2\\n4 1\\n4 2\\n2 3\\n-1 3\\n0 -1\\n\", \"4\\n0 0\\n9 1\\n1 3\\n0 1\\n\", \"6\\n2 -2\\n4 0\\n4 2\\n2 3\\n0 3\\n-1 -1\\n\", \"6\\n0 -1\\n4 0\\n4 2\\n2 3\\n1 2\\n0 0\\n\", \"6\\n2 -2\\n7 1\\n2 3\\n1 2\\n0 0\\n0 -1\\n\", \"5\\n2 -2\\n7 2\\n1 6\\n0 0\\n0 -1\\n\", \"4\\n2 -2\\n7 2\\n1 3\\n-1 0\\n\", \"5\\n2 -2\\n7 2\\n2 3\\n-1 0\\n0 -1\\n\", \"5\\n2 -2\\n7 1\\n2 3\\n1 2\\n-1 -1\\n\", \"4\\n0 0\\n2 3\\n1 2\\n0 1\\n\", \"5\\n0 0\\n1 0\\n2 0\\n4 2\\n1 6\\n\", \"4\\n1 -1\\n4 2\\n0 2\\n0 1\\n\", \"5\\n0 0\\n2 0\\n4 1\\n4 2\\n0 4\\n\", \"6\\n3 0\\n4 1\\n4 2\\n3 3\\n1 4\\n0 1\\n\", \"4\\n0 0\\n4 0\\n2 2\\n0 3\\n\", \"4\\n2 0\\n2 2\\n1 2\\n-1 1\\n\", \"5\\n0 0\\n3 0\\n4 1\\n3 6\\n0 2\\n\", \"4\\n2 -1\\n2 2\\n0 1\\n1 0\\n\", \"6\\n0 -1\\n2 0\\n4 1\\n4 2\\n2 5\\n0 3\\n\", \"4\\n0 0\\n2 0\\n6 0\\n1 3\\n\", \"4\\n0 1\\n1 1\\n3 2\\n-1 2\\n\", \"6\\n0 -2\\n4 1\\n4 2\\n2 3\\n1 3\\n0 -1\\n\", \"5\\n0 0\\n1 0\\n2 0\\n5 1\\n1 4\\n\", \"4\\n0 1\\n2 1\\n4 1\\n-1 2\\n\", \"5\\n2 -2\\n8 1\\n2 3\\n1 3\\n0 -1\\n\", \"4\\n0 0\\n2 0\\n25 1\\n1 3\\n\", \"6\\n2 -2\\n4 1\\n4 2\\n2 3\\n-1 2\\n0 -1\\n\", \"4\\n0 0\\n16 1\\n1 3\\n0 1\\n\", \"6\\n2 -3\\n4 0\\n4 2\\n2 3\\n0 3\\n-1 -1\\n\", \"6\\n0 -1\\n4 0\\n4 2\\n2 4\\n1 2\\n0 0\\n\", \"5\\n2 -2\\n7 1\\n1 2\\n0 0\\n0 -1\\n\", \"6\\n1 -2\\n4 0\\n7 2\\n1 6\\n0 0\\n0 -1\\n\", \"5\\n2 -2\\n7 2\\n1 3\\n0 2\\n-1 0\\n\", \"5\\n2 -2\\n7 2\\n2 3\\n-1 1\\n0 -1\\n\", \"4\\n0 0\\n2 3\\n0 2\\n0 1\\n\", \"5\\n0 0\\n1 0\\n2 0\\n4 2\\n1 12\\n\", \"4\\n1 -2\\n4 2\\n0 2\\n0 1\\n\", \"4\\n0 0\\n4 1\\n4 2\\n0 4\\n\", \"4\\n0 -1\\n4 0\\n2 2\\n0 3\\n\", \"3\\n2 0\\n2 2\\n-1 1\\n\", \"6\\n0 0\\n3 0\\n4 1\\n4 2\\n3 6\\n0 2\\n\", \"4\\n0 -1\\n1 0\\n2 2\\n0 1\\n\", \"6\\n-1 -1\\n2 0\\n4 1\\n4 2\\n2 5\\n0 3\\n\", \"4\\n0 1\\n1 1\\n4 2\\n-1 2\\n\", \"6\\n0 0\\n1 0\\n2 0\\n3 0\\n5 1\\n1 4\\n\", \"4\\n2 0\\n4 1\\n-1 2\\n0 1\\n\", \"6\\n2 -2\\n8 1\\n4 3\\n2 3\\n1 3\\n0 -1\\n\", \"6\\n2 -2\\n4 1\\n4 2\\n1 3\\n-1 2\\n0 -1\\n\", \"4\\n0 0\\n18 1\\n1 3\\n0 1\\n\", \"5\\n2 -3\\n4 0\\n4 2\\n0 3\\n-1 -1\\n\", \"4\\n2 -2\\n7 1\\n1 2\\n0 -1\\n\", \"6\\n1 -2\\n4 0\\n7 2\\n1 6\\n0 1\\n0 -1\\n\", \"5\\n2 -2\\n7 2\\n0 3\\n-1 1\\n0 -1\\n\", \"4\\n0 0\\n2 2\\n0 2\\n0 1\", \"5\\n0 0\\n2 1\\n4 2\\n3 3\\n1 3\"]}", "source": "taco"}
|
Find the convex hull of a given set of points P. In other words, find the smallest convex polygon containing all the points of P. Here, in a convex polygon, all interior angles are less than or equal to 180 degrees.
Please note that you should find all the points of P on both corner and boundary of the convex polygon.
Constraints
* 3 ≤ n ≤ 100000
* -10000 ≤ xi, yi ≤ 10000
* No point in the P will occur more than once.
Input
n
x1 y1
x2 y2
:
xn yn
The first integer n is the number of points in P. The coordinate of the i-th point pi is given by two integers xi and yi.
Output
In the first line, print the number of points on the corner/boundary of the convex polygon. In the following lines, print x y coordinates of the set of points. The coordinates should be given in the order of counter-clockwise visit of them starting from the point in P with the minimum y-coordinate, or the leftmost such point in case of a tie.
Examples
Input
7
2 1
0 0
1 2
2 2
4 2
1 3
3 3
Output
5
0 0
2 1
4 2
3 3
1 3
Input
4
0 0
2 2
0 2
0 1
Output
4
0 0
2 2
0 2
0 1
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n2 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 1\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 2\\n3 4\\n4 5\\n0 0\", \"6 6\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 2\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 2\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 6\\n3 4\\n2 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n3 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 1\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n4 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 4\\n2 4\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 3\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 2\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 6\\n2 3\\n3 4\\n4 5\\n3 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n2 3\\n2 4\\n5 4\\n1 2\\n1 3\\n3 3\\n4 5\\n0 0\", \"6 6\\n1 2\\n1 4\\n2 6\\n2 3\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n6 4\\n1 2\\n1 3\\n3 3\\n4 5\\n0 0\", \"6 9\\n3 2\\n1 4\\n2 6\\n2 3\\n3 4\\n4 5\\n3 6\\n2 1\\n1 2\\n3 3\\n1 1\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n1 3\\n3 3\\n4 5\\n0 0\", \"6 6\\n1 2\\n1 4\\n2 6\\n2 3\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 1\\n6 4\\n1 2\\n1 3\\n3 3\\n4 5\\n0 0\", \"6 13\\n1 1\\n1 4\\n2 4\\n2 5\\n5 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n1 3\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 3\\n2 3\\n3 4\\n2 2\\n0 0\", \"6 9\\n1 1\\n1 4\\n2 6\\n4 5\\n5 4\\n4 5\\n3 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n1 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 9\\n1 1\\n1 4\\n2 6\\n4 5\\n5 4\\n4 5\\n3 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n1 3\\n4 3\\n1 2\\n3 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n1 1\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 6\\n2 4\\n3 4\\n4 5\\n3 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n2 4\\n5 4\\n1 2\\n1 3\\n3 3\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 6\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n3 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n2 4\\n5 4\\n1 2\\n2 3\\n3 4\\n2 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 1\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n3 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n2 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n1 4\\n5 4\\n1 2\\n2 3\\n3 4\\n2 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 5\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 2\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n3 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n4 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n5 3\\n1 1\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 6\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 3\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n1 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n1 3\\n2 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 6\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n2 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 6\\n1 4\\n2 3\\n3 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n3 5\\n3 5\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n2 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 5\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 2\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 1\\n2 3\\n6 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n3 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 1\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n4 3\\n2 5\\n1 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n2 6\\n1 4\\n2 3\\n3 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 2\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n4 3\\n2 5\\n1 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n3 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 2\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 5\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 2\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n3 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 1\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 2\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n3 3\\n3 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n2 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n3 3\\n2 4\\n3 5\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n4 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 2\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 3\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n4 1\\n1 3\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 1\\n2 2\\n3 4\\n4 5\\n0 0\", \"6 6\\n1 2\\n1 4\\n2 3\\n2 4\\n3 3\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 6\\n2 5\\n3 4\\n5 3\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 6\\n3 4\\n2 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 6\\n1 4\\n2 3\\n3 5\\n3 4\\n4 5\\n6 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 4\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n3 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 1\\n2 3\\n6 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 3\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 2\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 1\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 5\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n3 3\\n3 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n2 2\\n1 3\\n2 3\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"10 7\\n1 4\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 2\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 1\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 4\\n3 4\\n5 4\\n1 2\\n2 5\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 6\\n3 4\\n2 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 1\\n2 3\\n2 3\\n4 3\\n1 2\\n3 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"10 7\\n1 4\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n2 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 6\\n3 4\\n1 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n2 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n1 4\\n5 4\\n1 2\\n2 3\\n3 4\\n2 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 2\\n3 4\\n5 4\\n1 2\\n1 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 1\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 6\\n1 2\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n4 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n1 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 1\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n4 3\\n2 5\\n1 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 2\\n1 4\\n2 4\\n2 6\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 2\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 1\\n5 4\\n1 2\\n2 5\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n4 1\\n1 3\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 4\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 6\\n1 5\\n2 3\\n3 5\\n3 4\\n4 5\\n6 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 4\\n1 4\\n2 3\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n1 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n3 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 1\\n2 3\\n6 4\\n5 4\\n1 3\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 3\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n3 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 2\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 4\\n2 1\\n1 1\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 5\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n3 3\\n3 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n2 1\\n1 3\\n2 3\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 6\\n2 3\\n2 6\\n3 4\\n2 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 3\\n4 3\\n1 2\\n3 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 6\\n3 4\\n2 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 1\\n2 3\\n2 3\\n6 3\\n1 2\\n3 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"10 7\\n1 4\\n1 4\\n2 4\\n2 4\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 2\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 4\\n1 4\\n2 3\\n2 5\\n6 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 1\\n2 3\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n5 5\\n4 6\\n4 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 1\\n4 3\\n1 4\\n2 4\\n3 4\\n5 4\\n1 2\\n2 3\\n1 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n4 3\\n2 5\\n1 4\\n4 4\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 4\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\", \"11 7\\n1 2\\n1 4\\n2 4\\n2 1\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n2 3\\n2 1\\n4 3\\n1 2\\n2 3\\n3 1\\n5 4\\n1 2\\n2 5\\n3 4\\n4 5\\n0 0\", \"6 7\\n1 2\\n1 4\\n2 3\\n2 5\\n3 4\\n4 5\\n4 6\\n2 1\\n1 2\\n3 3\\n1 2\\n1 3\\n2 3\\n4 3\\n1 2\\n2 3\\n3 4\\n5 4\\n1 2\\n2 3\\n3 4\\n4 5\\n0 0\"], \"outputs\": [\"2\\n1\\n2\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n0\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n0\\n0\\n\", \"2\\n1\\n2\\n0\\n1\\n1\\n0\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n0\\n\", \"0\\n0\\n1\\n1\\n0\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n0\\n\", \"0\\n0\\n1\\n1\\n0\\n0\\n\", \"2\\n1\\n2\\n0\\n1\\n1\\n0\\n\", \"0\\n0\\n1\\n1\\n0\\n\", \"2\\n1\\n2\\n0\\n0\\n0\\n\", \"0\\n1\\n1\\n0\\n\", \"0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n1\\n1\\n0\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n1\\n1\\n1\\n1\\n0\\n\", \"0\\n0\\n0\\n0\\n0\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n0\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n0\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n0\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n0\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n0\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n0\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n0\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n0\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n0\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n0\\n\", \"0\\n0\\n1\\n1\\n0\\n1\\n1\\n\", \"0\\n0\\n0\\n1\\n1\\n1\\n1\\n\", \"0\\n0\\n1\\n1\\n0\\n1\\n1\\n\", \"2\\n1\\n2\\n0\\n0\\n1\\n1\\n1\\n1\"]}", "source": "taco"}
|
Divide and rule
Taro, Hanako, and Jiro rule the JAG Kingdom together. There are N cities in the JAG Kingdom, some of which are connected by two-way roads. You can always reach all the other cities from any city via one or more roads.
One day, Taro and Hanako finally made a mistake and decided to share the city and govern it. However, I don't even like the fact that the city governed by Taro and the city governed by Hanako are directly connected by a single road because they have become so bad. Therefore, we decided to share the governing towns so as to satisfy the following conditions.
* Any pair of towns governed by Taro and Hanako are not directly connected by roads. This is because the relationship between Taro and Hanako is insanely bad.
* Towns governed by the same person are not directly connected by roads. This is to encourage diplomacy by obliging the passage under the control of others.
* The total number of towns governed by Taro and the total number of towns governed by Hanako must be the same. This is because if the total number is not equal, the relationship between Taro and Hanako will be even worse. Here, Mr. Jiro is very open-minded, so the total number of cities governed by Mr. Jiro can be any number.
If the division meets the above conditions, the three people can be convinced to rule, and even if there are no cities governed by someone, there is no complaint. At this time, create a program that enumerates all possible numbers as the total number of cities governed by Mr. Taro (= the total number of cities governed by Mr. Hanako).
Input
The input consists of multiple datasets. The maximum number of datasets is 50. Each data set is represented in the following format.
> N M u1 v1 ... uM vM
The first line consists of two integers N (2 ≤ N ≤ 103) and M (1 ≤ M ≤ 103), which represent the number of cities and the number of roads, respectively. The i-th line of the following M lines consists of two integers ui and vi (1 ≤ ui <vi ≤ N), indicating that the i-th road connects the city ui and the city vi in both directions. Here, it is guaranteed that one city can always reach all other cities via one or more roads. Also, no multiple roads connecting pairs of the same city will be given. That is, (ui, vi) ≠ (uj, vj) is satisfied for all 1 ≤ i <j ≤ M.
The end of the input is represented by a line of two zeros.
Output
For each dataset, if there are K possible total numbers of cities governed by Taro, first output K on the first line, then output the possible total number on each line in ascending order.
Sample Input
6 7
1 2
14
twenty three
twenty five
3 4
4 5
4 6
twenty one
1 2
3 3
1 2
13
twenty three
4 3
1 2
twenty three
3 4
5 4
1 2
twenty three
3 4
4 5
0 0
Output for the Sample Input
2
1
2
0
0
1
1
1
1
Example
Input
6 7
1 2
1 4
2 3
2 5
3 4
4 5
4 6
2 1
1 2
3 3
1 2
1 3
2 3
4 3
1 2
2 3
3 4
5 4
1 2
2 3
3 4
4 5
0 0
Output
2
1
2
0
0
1
1
1
1
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"12 5 3\\n100 9999 98\\n10000 10000 10000\\n0 0 0\", \"12 2 3\\n100 9999 98\\n10000 10000 10000\\n0 0 0\", \"12 2 3\\n100 15522 98\\n10000 10000 10000\\n0 0 0\", \"12 2 3\\n100 15914 98\\n10000 10000 10000\\n0 0 0\", \"12 2 3\\n100 15914 98\\n10001 10000 10000\\n0 0 0\", \"12 2 3\\n100 15914 12\\n10001 10000 10000\\n0 0 0\", \"12 2 3\\n100 7953 12\\n10001 10000 10000\\n0 0 0\", \"12 2 3\\n101 7953 12\\n10001 10000 10000\\n0 0 0\", \"12 2 3\\n100 9999 98\\n10100 10000 10000\\n0 0 0\", \"12 2 3\\n100 15914 12\\n10001 10001 10000\\n0 0 0\", \"12 1 3\\n100 7953 12\\n10001 10000 10000\\n0 0 0\", \"12 4 3\\n100 7953 12\\n10001 10000 10000\\n0 0 0\", \"12 2 3\\n100 14468 12\\n10001 10001 10000\\n0 0 0\", \"12 1 3\\n100 7953 12\\n10001 10001 10000\\n0 0 0\", \"12 2 3\\n100 4467 12\\n10001 10001 10000\\n0 0 0\", \"8 5 3\\n101 9999 98\\n10000 10000 10000\\n0 0 0\", \"12 1 3\\n100 9999 98\\n10000 10000 10000\\n0 0 0\", \"12 2 3\\n100 15522 39\\n10000 10000 10000\\n0 0 0\", \"12 2 3\\n101 15914 98\\n10001 10000 10000\\n0 0 0\", \"12 2 3\\n100 9999 98\\n10100 10000 10100\\n0 0 0\", \"12 2 3\\n100 8550 12\\n10001 10001 10000\\n0 0 0\", \"12 2 3\\n100 14468 12\\n10101 10001 10000\\n0 0 0\", \"12 1 3\\n100 7953 14\\n10001 10001 10000\\n0 0 0\", \"8 3 3\\n101 9999 98\\n10000 10000 10000\\n0 0 0\", \"12 2 3\\n100 27346 12\\n10101 10001 10000\\n0 0 0\", \"12 5 3\\n100 9999 98\\n10000 11000 10000\\n0 0 0\", \"12 4 3\\n100 9999 98\\n10000 10000 10000\\n0 0 0\", \"12 2 3\\n110 15914 98\\n10000 10000 10000\\n0 0 0\", \"12 2 6\\n100 15914 12\\n10001 10000 10000\\n0 0 0\", \"10 2 3\\n100 7953 12\\n10001 10000 10000\\n0 0 0\", \"12 2 3\\n101 395 12\\n10001 10000 10000\\n0 0 0\", \"12 2 3\\n100 9999 98\\n10100 10001 10000\\n0 0 0\", \"18 2 3\\n100 15914 12\\n10001 10001 10000\\n0 0 0\", \"12 1 3\\n100 7953 12\\n10001 10001 10001\\n0 0 0\", \"12 2 3\\n100 4467 12\\n10001 10001 10001\\n0 0 0\", \"12 2 3\\n100 15522 39\\n10010 10000 10000\\n0 0 0\", \"12 2 3\\n101 15914 98\\n10101 10000 10000\\n0 0 0\", \"12 2 3\\n101 7953 12\\n10001 10010 10000\\n0 0 0\", \"7 2 3\\n100 8550 12\\n10001 10001 10000\\n0 0 0\", \"12 2 3\\n100 19834 12\\n10101 10001 10000\\n0 0 0\", \"12 2 3\\n100 27346 12\\n11101 10001 10000\\n0 0 0\", \"12 10 3\\n100 9999 98\\n10000 11000 10000\\n0 0 0\", \"12 2 1\\n110 15914 98\\n10000 10000 10000\\n0 0 0\", \"12 2 6\\n100 15914 12\\n10011 10000 10000\\n0 0 0\", \"3 2 3\\n100 7953 12\\n10001 10000 10000\\n0 0 0\", \"18 2 3\\n101 15914 12\\n10001 10001 10000\\n0 0 0\", \"17 2 3\\n100 4467 12\\n10001 10001 10001\\n0 0 0\", \"12 2 3\\n101 15522 39\\n10010 10000 10000\\n0 0 0\", \"12 4 3\\n101 15914 98\\n10101 10000 10000\\n0 0 0\", \"10 2 3\\n100 8550 12\\n10001 10001 10000\\n0 0 0\", \"12 2 1\\n100 27346 12\\n11101 10001 10000\\n0 0 0\", \"12 10 3\\n100 9999 98\\n10000 11010 10000\\n0 0 0\", \"12 2 2\\n100 15914 12\\n10011 10000 10000\\n0 0 0\", \"3 2 3\\n100 7953 12\\n10001 10010 10000\\n0 0 0\", \"18 2 4\\n101 15914 12\\n10001 10001 10000\\n0 0 0\", \"12 2 3\\n101 15522 39\\n11010 10000 10000\\n0 0 0\", \"12 4 2\\n101 15914 98\\n10101 10000 10000\\n0 0 0\", \"12 2 3\\n100 15914 12\\n10011 10000 10000\\n0 0 0\", \"12 4 2\\n101 15914 98\\n10101 10000 10100\\n0 0 0\", \"12 2 3\\n101 15914 12\\n10011 10000 10000\\n0 0 0\", \"16 5 3\\n100 9999 98\\n10000 10000 10000\\n0 0 0\", \"12 5 3\\n100 9999 98\\n10000 10100 10000\\n0 0 0\", \"7 2 3\\n100 15914 98\\n10000 10000 10000\\n0 0 0\", \"12 2 3\\n101 7953 12\\n10001 10100 10000\\n0 0 0\", \"12 2 3\\n100 9999 52\\n10100 10000 10000\\n0 0 0\", \"12 2 3\\n101 15914 12\\n10001 10001 10000\\n0 0 0\", \"12 2 3\\n101 14468 12\\n10001 10001 10000\\n0 0 0\", \"4 2 3\\n100 4467 12\\n10001 10001 10000\\n0 0 0\", \"12 3 3\\n101 7214 12\\n10001 10000 10000\\n0 0 0\", \"12 2 4\\n100 8550 12\\n10001 10001 10000\\n0 0 0\", \"12 2 3\\n100 14468 12\\n11101 10001 10000\\n0 0 0\", \"12 2 2\\n100 27346 12\\n11101 10001 10000\\n0 0 0\", \"8 1 3\\n100 7953 14\\n10001 10101 10000\\n0 0 0\", \"12 5 3\\n100 16220 98\\n10000 11000 10000\\n0 0 0\", \"12 2 3\\n101 15914 98\\n10000 10000 10000\\n0 0 0\", \"21 2 6\\n100 15914 12\\n10001 10000 10000\\n0 0 0\", \"10 2 4\\n100 7953 12\\n10001 10000 10000\\n0 0 0\", \"12 2 3\\n101 395 12\\n10001 11000 10000\\n0 0 0\", \"18 2 3\\n100 15914 12\\n10001 11001 10000\\n0 0 0\", \"12 1 4\\n100 7953 12\\n10001 10001 10000\\n0 0 0\", \"12 2 3\\n100 4467 12\\n10001 00001 10001\\n0 0 0\", \"5 1 3\\n100 9999 98\\n10010 10000 10000\\n0 0 0\", \"12 1 3\\n100 15522 39\\n10010 10000 10000\\n0 0 0\", \"12 1 3\\n101 15914 98\\n10101 10000 10000\\n0 0 0\", \"5 2 3\\n100 19834 12\\n10101 10001 10000\\n0 0 0\", \"12 2 3\\n100 27346 12\\n11001 10001 10000\\n0 0 0\", \"3 10 3\\n100 9999 98\\n10000 11000 10000\\n0 0 0\", \"5 2 3\\n100 7953 12\\n10001 10000 10000\\n0 0 0\", \"18 2 3\\n111 15914 12\\n10001 10001 10000\\n0 0 0\", \"17 2 3\\n100 4467 9\\n10001 10001 10001\\n0 0 0\", \"12 2 3\\n101 13902 39\\n10010 10000 10000\\n0 0 0\", \"12 4 3\\n111 15914 98\\n10101 10000 10000\\n0 0 0\", \"12 2 2\\n100 15914 12\\n10011 10001 10000\\n0 0 0\", \"3 2 3\\n100 7953 12\\n10101 10010 10000\\n0 0 0\", \"18 2 4\\n111 15914 12\\n10001 10001 10000\\n0 0 0\", \"12 4 4\\n101 15914 98\\n10101 10000 10000\\n0 0 0\", \"12 2 3\\n100 15914 11\\n10011 10000 10000\\n0 0 0\", \"12 2 3\\n101 15914 12\\n10011 10100 10000\\n0 0 0\", \"16 5 3\\n100 9999 98\\n10000 10001 10000\\n0 0 0\", \"12 5 3\\n100 13134 98\\n10000 10100 10000\\n0 0 0\", \"8 5 3\\n100 9999 98\\n10000 10000 10000\\n0 0 0\"], \"outputs\": [\"11\\n93\\n2019\\n\", \"10\\n93\\n2019\\n\", \"10\\n89\\n2019\\n\", \"10\\n16\\n2019\\n\", \"10\\n16\\n2018\\n\", \"10\\n30\\n2018\\n\", \"10\\n17\\n2018\\n\", \"10\\n70\\n2018\\n\", \"10\\n93\\n7033\\n\", \"10\\n30\\n8812\\n\", \"2\\n17\\n2018\\n\", \"12\\n17\\n2018\\n\", \"10\\n89\\n8812\\n\", \"2\\n17\\n8812\\n\", \"10\\n80\\n8812\\n\", \"1\\n91\\n2019\\n\", \"2\\n93\\n2019\\n\", \"10\\n30\\n2019\\n\", \"10\\n29\\n2018\\n\", \"10\\n93\\n7133\\n\", \"10\\n28\\n8812\\n\", \"10\\n89\\n3762\\n\", \"2\\n19\\n8812\\n\", \"7\\n91\\n2019\\n\", \"10\\n15\\n3762\\n\", \"11\\n93\\n6511\\n\", \"12\\n93\\n2019\\n\", \"10\\n5\\n2019\\n\", \"1\\n30\\n2018\\n\", \"6\\n17\\n2018\\n\", \"10\\n34\\n2018\\n\", \"10\\n93\\n3862\\n\", \"6\\n30\\n8812\\n\", \"2\\n17\\n8813\\n\", \"10\\n80\\n8813\\n\", \"10\\n30\\n1964\\n\", \"10\\n29\\n6932\\n\", \"10\\n70\\n1012\\n\", \"1\\n28\\n8812\\n\", \"10\\n71\\n3762\\n\", \"10\\n15\\n4251\\n\", \"10\\n93\\n6511\\n\", \"8\\n5\\n2019\\n\", \"1\\n30\\n1953\\n\", \"1\\n17\\n2018\\n\", \"6\\n44\\n8812\\n\", \"4\\n80\\n8813\\n\", \"10\\n52\\n1964\\n\", \"12\\n29\\n6932\\n\", \"6\\n28\\n8812\\n\", \"8\\n15\\n4251\\n\", \"10\\n93\\n6514\\n\", \"9\\n30\\n1953\\n\", \"1\\n17\\n1012\\n\", \"7\\n44\\n8812\\n\", \"10\\n52\\n3278\\n\", \"11\\n29\\n6932\\n\", \"10\\n30\\n1953\\n\", \"11\\n29\\n7032\\n\", \"10\\n44\\n1953\\n\", \"4\\n93\\n2019\\n\", \"11\\n93\\n8499\\n\", \"1\\n16\\n2019\\n\", \"10\\n70\\n8598\\n\", \"10\\n47\\n7033\\n\", \"10\\n44\\n8812\\n\", \"10\\n57\\n8812\\n\", \"2\\n80\\n8812\\n\", \"10\\n22\\n2018\\n\", \"11\\n28\\n8812\\n\", \"10\\n89\\n4251\\n\", \"9\\n15\\n4251\\n\", \"2\\n19\\n4403\\n\", \"11\\n30\\n6511\\n\", \"10\\n29\\n2019\\n\", \"15\\n30\\n2018\\n\", \"7\\n17\\n2018\\n\", \"10\\n34\\n7510\\n\", \"6\\n30\\n2994\\n\", \"3\\n17\\n8812\\n\", \"10\\n80\\n10000\\n\", \"2\\n93\\n1964\\n\", \"2\\n30\\n1964\\n\", \"2\\n29\\n6932\\n\", \"4\\n71\\n3762\\n\", \"10\\n15\\n9819\\n\", \"1\\n93\\n6511\\n\", \"4\\n17\\n2018\\n\", \"6\\n103\\n8812\\n\", \"4\\n77\\n8813\\n\", \"10\\n74\\n1964\\n\", \"12\\n78\\n6932\\n\", \"9\\n30\\n8757\\n\", \"1\\n17\\n6918\\n\", \"7\\n103\\n8812\\n\", \"1\\n29\\n6932\\n\", \"10\\n29\\n1953\\n\", \"10\\n44\\n9533\\n\", \"4\\n93\\n8812\\n\", \"11\\n33\\n8499\\n\", \"1\\n93\\n2019\"]}", "source": "taco"}
|
Let’s play a stone removing game.
Initially, n stones are arranged on a circle and numbered 1, ... , n clockwise (Figure 1). You are also given two numbers k and m. From this state, remove stones one by one following the rules explained below, until only one remains. In step 1, remove stone m. In step 2, locate the k-th next stone clockwise from m and remove it. In subsequent steps, start from the slot of the stone removed in the last step, make k hops clockwise on the remaining stones and remove the one you reach. In other words, skip (k - 1) remaining stones clockwise and remove the next one. Repeat this until only one stone is left and answer its number.
For example, the answer for the case n = 8, k = 5, m = 3 is 1, as shown in Figure 1.
<image>
Figure 1: An example game
Initial state: Eight stones are arranged on a circle.
Step 1: Stone 3 is removed since m = 3.
Step 2: You start from the slot that was occupied by stone 3. You skip four stones 4, 5, 6 and 7 (since k = 5), and remove the next one, which is 8.
Step 3: You skip stones 1, 2, 4 and 5, and thus remove 6. Note that you only count stones that are still on the circle and ignore those already removed. Stone 3 is ignored in this case.
Steps 4-7: You continue until only one stone is left. Notice that in later steps when only a few stones remain, the same stone may be skipped multiple times. For example, stones 1 and 4 are skipped twice in step 7.
Final State: Finally, only one stone, 1, is on the circle. This is the final state, so the answer is 1.
Input
The input consists of multiple datasets each of which is formatted as follows.
n k m
The last dataset is followed by a line containing three zeros. Numbers in a line are separated by a single space. A dataset satisfies the following conditions.
2 ≤ n ≤ 10000, 1 ≤ k ≤ 10000, 1 ≤ m ≤ n
The number of datasets is less than 100.
Output
For each dataset, output a line containing the stone number left in the final state. No extra characters such as spaces should appear in the output.
Example
Input
8 5 3
100 9999 98
10000 10000 10000
0 0 0
Output
1
93
2019
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.5
|
{"tests": "{\"inputs\": [\"7\\nafxfxfg\\n3\\nf 3\\nx 2\\nfxf 6\\n1\\n\", \"11\\nfghdgrakmnq\\n8\\nfgh 4\\ngh 3\\nh 10\\nhdg 6\\nhdgra 7\\nakm 12\\nrakm 5\\na 15\\n3\\n\", \"6\\nabacba\\n5\\naba 6\\nba 3\\nbac 4\\ncb 3\\nc 6\\n1\\n\", \"8\\naxghcdex\\n5\\naxgh 13\\nhc 35\\ncde 17\\nxghcd 29\\nghcdex 30\\n3\\n\", \"6\\nabacba\\n5\\naba 6\\nba 3\\nbac 4\\ncb 3\\nc 6\\n2\\n\", \"6\\nabacba\\n2\\naba 6\\nba 3\\n1\\n\", \"7\\nafxfxfg\\n3\\nf 5\\nx 2\\nfxf 6\\n1\\n\", \"11\\nfghdgrakmnq\\n8\\nfgh 4\\ngh 3\\nh 10\\nhdg 6\\nargdh 7\\nakm 12\\nrakm 5\\na 15\\n3\\n\", \"6\\nabacba\\n5\\naba 6\\nba 4\\nbac 4\\ncb 3\\nc 6\\n2\\n\", \"6\\nabacba\\n2\\naba 6\\nba 3\\n2\\n\", \"11\\nfghdgrakmnq\\n8\\nfgh 4\\ngh 3\\nh 10\\nhdg 6\\nargdh 7\\nakm 12\\nrakm 5\\na 15\\n6\\n\", \"6\\nabacba\\n5\\naba 6\\nba 4\\nbac 8\\ncb 3\\nc 6\\n2\\n\", \"6\\nabacba\\n2\\naba 6\\nba 4\\n2\\n\", \"6\\nabacba\\n2\\naba 5\\nba 4\\n2\\n\", \"6\\nabacba\\n5\\naba 0\\nba 4\\nbac 1\\ncb 3\\nc 6\\n2\\n\", \"6\\nabacba\\n2\\naba 5\\nba 0\\n2\\n\", \"6\\nabacba\\n5\\naba 0\\nba 4\\nbac 1\\nbc 3\\nc 6\\n2\\n\", \"6\\nabacba\\n5\\naba 0\\nba 1\\nbac 1\\nbc 3\\nc 6\\n2\\n\", \"6\\nabacba\\n2\\nbaa 5\\nab 0\\n2\\n\", \"6\\nabacba\\n2\\nbaa 5\\nba 1\\n2\\n\", \"6\\nabacba\\n2\\nbaa 5\\nba 2\\n2\\n\", \"7\\naexfxfg\\n3\\nf 3\\nx 2\\nfxf 6\\n1\\n\", \"11\\nfghdgrakmnq\\n8\\nfgh 4\\ngh 3\\nh 10\\nhdg 6\\nhdgra 7\\nmka 12\\nrakm 5\\na 15\\n3\\n\", \"6\\nabacba\\n5\\naba 6\\nba 3\\nbca 4\\ncb 3\\nc 6\\n2\\n\", \"6\\nabacba\\n2\\naba 8\\nba 3\\n1\\n\", \"11\\nfghdgrakmnq\\n8\\nfgh 4\\ngh 3\\nh 10\\nhdg 6\\nargdh 7\\nakm 12\\nralm 5\\na 15\\n3\\n\", \"6\\nabacba\\n5\\naba 6\\nba 4\\nbac 4\\ncb 6\\nc 6\\n2\\n\", \"11\\nqnmkargdhgf\\n8\\nfgh 4\\ngh 3\\nh 10\\nhdg 6\\nhdgra 7\\nmka 12\\nrakm 5\\na 15\\n3\\n\", \"6\\nabacba\\n5\\naca 6\\nba 6\\nbac 4\\ncb 3\\nc 6\\n1\\n\", \"8\\naxhhcdex\\n5\\naxgh 13\\nhc 35\\ncde 34\\nxghcd 29\\nghcdex 30\\n3\\n\", \"6\\nabacba\\n5\\naba 6\\nba 3\\nbca 4\\ncb 4\\nc 6\\n2\\n\", \"6\\nabacba\\n5\\naba 6\\nba 4\\nbac 1\\ncb 3\\nc 6\\n2\\n\", \"6\\nabacba\\n2\\naba 5\\nab 0\\n2\\n\", \"6\\nabacba\\n2\\nbaa 5\\nba 0\\n2\\n\", \"6\\nabacba\\n2\\nbab 5\\nba 2\\n2\\n\", \"6\\nabacba\\n5\\naca 6\\nba 3\\nbac 4\\ncb 3\\nc 6\\n1\\n\", \"8\\naxhhcdex\\n5\\naxgh 13\\nhc 35\\ncde 17\\nxghcd 29\\nghcdex 30\\n3\\n\", \"6\\nabacba\\n2\\naba 6\\nba 2\\n3\\n\", \"7\\nafxfxfg\\n3\\nf 5\\nx 2\\nfxf 0\\n1\\n\", \"6\\nabacba\\n2\\naba 6\\nba 4\\n0\\n\", \"11\\nfghdgrakmmq\\n8\\nfgh 4\\ngh 3\\nh 10\\nhdg 6\\nargdh 7\\nakm 12\\nrakm 5\\na 15\\n6\\n\", \"6\\nabacba\\n2\\naba 6\\nab 4\\n2\\n\", \"6\\nabacba\\n5\\naba 6\\nba 4\\ncab 1\\ncb 3\\nc 6\\n2\\n\", \"6\\nabcaba\\n2\\naba 5\\nba 4\\n2\\n\", \"6\\nabacba\\n5\\naba 0\\nba 4\\nbac 1\\ncb 3\\nc 8\\n2\\n\", \"6\\nabacba\\n2\\naba 5\\nbb 0\\n2\\n\", \"6\\nabacba\\n2\\naba 5\\nab 0\\n0\\n\", \"6\\nbbacba\\n5\\naba 0\\nba 1\\nbac 1\\nbc 3\\nc 6\\n2\\n\", \"6\\nababba\\n2\\nbaa 5\\nab 0\\n2\\n\", \"6\\nabacba\\n2\\nbaa 2\\nba 0\\n2\\n\", \"6\\nabacba\\n2\\nbab 5\\nba 2\\n4\\n\", \"7\\ngfxfxea\\n3\\nf 3\\nx 2\\nfxf 6\\n1\\n\", \"7\\ngfxfxfa\\n3\\nf 5\\nx 2\\nfxf 0\\n1\\n\", \"6\\nabacba\\n2\\naba 6\\nba 3\\n3\\n\"], \"outputs\": [\"13\\n\", \"52\\n\", \"15\\n\", \"95\\n\", \"21\\n\", \"9\\n\", \"19\\n\", \"52\\n\", \"23\\n\", \"12\\n\", \"55\\n\", \"24\\n\", \"14\\n\", \"13\\n\", \"17\\n\", \"5\\n\", \"15\\n\", \"9\\n\", \"0\\n\", \"2\\n\", \"4\\n\", \"10\\n\", \"43\\n\", \"21\\n\", \"11\\n\", \"47\\n\", \"26\\n\", \"37\\n\", \"18\\n\", \"69\\n\", \"22\\n\", \"23\\n\", \"5\\n\", \"0\\n\", \"4\\n\", \"12\\n\", \"52\\n\", \"10\\n\", \"19\\n\", \"0\\n\", \"55\\n\", \"10\\n\", \"23\\n\", \"9\\n\", \"19\\n\", \"5\\n\", \"0\\n\", \"9\\n\", \"0\\n\", \"0\\n\", \"4\\n\", \"10\\n\", \"19\\n\", \"12\\n\"]}", "source": "taco"}
|
You have recently fallen through a hole and, after several hours of unconsciousness, have realized you are in an underground city. On one of your regular, daily walks through the unknown, you have encountered two unusually looking skeletons called Sanz and P’pairus, who decided to accompany you and give you some puzzles for seemingly unknown reasons.
One day, Sanz has created a crossword for you. Not any kind of crossword, but a 1D crossword! You are given m words and a string of length n. You are also given an array p, which designates how much each word is worth — the i-th word is worth pi points. Whenever you find one of the m words in the string, you are given the corresponding number of points. Each position in the crossword can be used at most x times. A certain word can be counted at different places, but you cannot count the same appearance of a word multiple times. If a word is a substring of another word, you can count them both (presuming you haven’t used the positions more than x times).
In order to solve the puzzle, you need to tell Sanz what’s the maximum achievable number of points in the crossword. There is no need to cover all postions, just get the maximal score! Crossword and words contain only lowercase English letters.
Input
The first line of the input contains a single integer n (1 ≤ n ≤ 500) — the length of the crossword. The second line contains the crossword string. The third line contains a single integer m (1 ≤ m ≤ 100) — the number of given words, and next m lines contain description of words: each line will have a string representing a non-empty word (its length doesn't exceed the length of the crossword) and integer pi (0 ≤ pi ≤ 100). Last line of the input will contain x (1 ≤ x ≤ 100) — maximum number of times a position in crossword can be used.
Output
Output single integer — maximum number of points you can get.
Example
Input
6
abacba
2
aba 6
ba 3
3
Output
12
Note
For example, with the string "abacba", words "aba" (6 points) and "ba" (3 points), and x = 3, you can get at most 12 points - the word "aba" appears once ("abacba"), while "ba" appears two times ("abacba"). Note that for x = 1, you could get at most 9 points, since you wouldn’t be able to count both "aba" and the first appearance of "ba".
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 3\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 2\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 1\\nRRRRR\\n2 9 2\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 2\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\n.RRR\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\n.RRR\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 19\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 2\\n.R..R..R.\\n.R..R..R.\\n7 4 3\\nR.RR\\n.RRR\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRR.R.\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 11\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\nR....\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 45\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 12\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR.R..\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 2\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 10\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 10\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 7\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 19\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 12\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\nR....\\n6 4 2\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 45\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 12\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nRR..\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 2\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 7\\nRRR..\\nR.R..\\nRR.R.\\nR..R.\\nR...R\\n2 31 19\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 12\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 10\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 5\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\n.RRR\\nRRR.\\nR.R.\\n...R\\nRRRR\\nRRRR\\nRR.R\\n1 1 1\\nR\\n\", \"5\\n2 6 1\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 2\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 2\\n.R..R..R.\\n.R..R..R.\\n7 4 5\\nR.RR\\n.RRR\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\n..RRR\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\n.RR.R\\nR..R.\\nR...R\\n2 31 19\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 4\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n....R\\n...R.\\n.R...\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 11\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nRR..\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 5\\nRRR..\\n..R.R\\n..RRR\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 3\\n.R..R..R.\\n.R..R..R.\\n7 4 3\\nR.RR\\n.RRR\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 8\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRR.R.\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nRR..\\n...R\\nRRRR\\nRRRR\\nRR.R\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 18\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 2\\n..R..\\n...R.\\n....R\\n6 4 2\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\n.RR.R\\n.R..R\\nR...R\\n2 31 19\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n....R\\n...R.\\n.R...\\n6 4 6\\nR..R\\nRR..\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nRR...\\n2 31 11\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 5\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 3\\n.R..R..R.\\n.R..R..R.\\n7 4 3\\nR.RR\\n.RRR\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n....R\\n...R.\\n.R...\\n6 4 6\\nR..R\\nRR..\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nRR...\\n1 31 11\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n.R...\\n....R\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 5\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 2\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 5\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 19\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 9\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\nR....\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 7\\nRRR..\\n.RR..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\n.RR.R\\nR..R.\\nR...R\\n2 31 4\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nRR..\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\n..R.R\\n..RRR\\nR..R.\\nR...R\\n2 31 24\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\n..RR.\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n....R\\n...R.\\n.R...\\n6 4 6\\nR..R\\nRR..\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nRR...\\n2 31 18\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\n.RR.R\\n.R..R\\nR...R\\n2 31 4\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 2\\nRRRRR\\n2 9 2\\n.RR....R.\\n....RR.R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\n...R\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 1\\nRRRRR\\n2 9 2\\n.R....RR.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR.R..\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nRR.R\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\nR....\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\n.RRR\\nR.R.\\nR...\\nRRRR\\nRRRR\\nRR.R\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\n.RR..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR.R..\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\n...R\\nRRRR\\nRRRR\\nRR.R\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\nR....\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\n.RR..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 2\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.RR.R....\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\nR....\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRR.R.\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\n.RRR\\nRRR.\\nR.R.\\n...R\\nRRRR\\nRRRR\\nRR.R\\n1 1 1\\nR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 2\\nRRRRR\\n2 9 1\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nRR.R\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\nR....\\n6 4 2\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 2\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\n..R.R\\n2 31 45\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 1\\nRRRRRR\\nRRRRRR\\n1 5 3\\nRRRRR\\n2 9 2\\n.R..R..R.\\n.R..R..R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nRR.R\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\n..R.R\\n..RRR\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 4\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\n..RRR\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n....R\\n...R.\\n.R...\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nRR...\\n2 31 11\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nRR..\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\n..R.R\\n..RRR\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 1\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\n..RR.\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nR.R.R\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 1\\nRRRRR\\n2 9 2\\n.R....RR.\\n....RR.R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 4\\nR..R\\nR..R\\nRRRR\\nRRRR\\n.R.R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\nR....\\n6 4 1\\nRR..\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 5\\nRRR..\\n..R.R\\n..RRR\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nR.R.R\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 1\\nRRRRR\\n2 9 2\\n.RR....R.\\n....RR.R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\nR...\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n.R...\\n6 4 4\\nR..R\\nR..R\\nRRRR\\nRRRR\\n.R.R\\nR..R\\n5 5 1\\nRRR..\\nR.R..\\nRRR..\\n.R..R\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\", \"5\\n2 6 3\\nRRRRRR\\nRRRRRR\\n1 5 1\\nRRRRR\\n2 9 2\\n.RR....R.\\n....RR.R.\\n7 4 10\\nR.RR\\nRRR.\\nR.R.\\n...R\\nRRRR\\nRRRR\\nR.RR\\n1 1 1\\nR\\n\", \"4\\n3 5 3\\n..R..\\n...R.\\n....R\\n6 4 6\\nR..R\\nR..R\\nRRRR\\nRRRR\\nR..R\\nR..R\\n5 5 4\\nRRR..\\nR.R..\\nRRR..\\nR..R.\\nR...R\\n2 31 62\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\nRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR\\n\"], \"outputs\": [\"aaaabb\\nccccbb\\naabbc\\naaaaabbbb\\ncccccccbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaaa\\naaaaaaaaa\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaaabb\\nccccbb\\naaaaa\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaab\\nbbbbbbbbb\\naaab\\ndccb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaaa\\naaaaaaaaa\\naaab\\ndccb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\naaaabbbbccccddddeeeefffggghhhii\\nsssrrrqqqpppooonnnmmmlllkkkjjji\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaab\\nbbbbbbbbb\\naaaa\\naaaa\\nabbb\\nbbbb\\nbbbb\\ncccb\\ncccc\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaab\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaaabbbbbbccccccddddddeeeeeef\\nkkkkkjjjjjiiiiihhhhhggggggfffff\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\naabbccddeeffgghhiijjkkllmmnnoop\\nSRQPONMLKJIHGFEDCBAzyxwvutsrqqp\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbbb\\nccdd\\nhgfe\\nijjj\\nlllk\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naaabb\\naaaaaaaaa\\naaaaaaaaa\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\naaaaaaabbbbbbbccccccddddddeeeee\\njjjjjjiiiiiihhhhhhggggggffffffe\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbbb\\nccdd\\nffee\\nghhh\\njjji\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naabbb\\nccbbb\\ncddee\\neeeee\\nfgggg\\naaaabbbbccccddddeeeefffggghhhii\\nsssrrrqqqpppooonnnmmmlllkkkjjji\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbbb\\nccdd\\nhgfe\\nijjj\\nlllk\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\nbbbb\\nbbbb\\nbbbb\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\naabbccddeeffgghhiijjkkllmmnnoop\\nSRQPONMLKJIHGFEDCBAzyxwvutsrqqp\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbbb\\nccdd\\nhgfe\\nijjj\\nlllk\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeff\\nffff\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\nbbbb\\nbbbb\\nbbbb\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naabbb\\nccbbb\\ncddde\\neeeee\\nfgggg\\naaaabbbbccccddddeeeefffggghhhii\\nsssrrrqqqpppooonnnmmmlllkkkjjji\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbbb\\nccdd\\nhgfe\\nijjj\\nlllk\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\naaaaaaabbbbbbbccccccddddddeeeee\\njjjjjjiiiiiihhhhhhggggggffffffe\\n\", \"aaabbb\\needdcc\\naabbc\\naaaaaaaaa\\naaaaaaaaa\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaaaaa\\naaaaaa\\naabbc\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaab\\nbbbbbbbbb\\naaaa\\nbbba\\nbbbc\\ncccc\\ncccd\\neddd\\neeee\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbbcc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbccc\\ndddcc\\nddddd\\naaaabbbbccccddddeeeefffggghhhii\\nsssrrrqqqpppooonnnmmmlllkkkjjji\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\nbbbb\\ncccc\\ndddd\\ndddd\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaaa\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaaabbbbbbccccccddddddeeeeeef\\nkkkkkjjjjjiiiiihhhhhggggggfffff\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbbcc\\nddddd\\neeeee\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaabbbb\\ncccccccbb\\naaaa\\naaaa\\nabbb\\nbbbb\\nbbbb\\ncccb\\ncccc\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbbb\\nccdd\\nffee\\ngggg\\nhhhh\\naaaab\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaaa\\naaaaaaaaa\\naaab\\nccbb\\nddee\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\naaaabbbbccccddddeeeeffffgggghhh\\nrrrqqqpppooonnnmmmlllkkkjjjiiih\\n\", \"aaaaa\\nbbbaa\\nbbbbb\\naaaa\\naaaa\\naaaa\\nbbbb\\nbbbb\\nbbbb\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbccc\\nddddc\\nddddd\\naaaabbbbccccddddeeeefffggghhhii\\nsssrrrqqqpppooonnnmmmlllkkkjjji\\n\", \"aaaaa\\ncccbb\\nccccc\\naaaa\\nbaaa\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaaabbbbbbccccccddddddeeeeeef\\nkkkkkjjjjjiiiiihhhhhggggggfffff\\n\", \"aaabbb\\needdcc\\naabbc\\naaaaabbbb\\ncccccccbb\\naaaa\\naaaa\\nabbb\\nbbbb\\nbbbb\\ncccb\\ncccc\\na\\n\", \"aaaaa\\ncccbb\\nccccc\\naaaa\\nbaaa\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaabbbcccdddeeefffggghhhiiijjkk\\n\", \"aaabb\\ncbbbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabbb\\needdcc\\naabbc\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbccdd\\nddddd\\neeeee\\naaaabbbbccccddddeeeefffggghhhii\\nsssrrrqqqpppooonnnmmmlllkkkjjji\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbbb\\nccdd\\nffee\\ngggg\\niiih\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naabbb\\nccbbb\\ncddee\\neeeee\\nfgggg\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbccc\\ndddcc\\nddddd\\naaaaaaaaaaaaaaaabbbbbbbbbbbbbbb\\ndddddddddddddddcccccccccccccccb\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbbcc\\ndddcc\\nddddd\\naaabbbcccdddeeefffggghhhiiijjjk\\nxxwwvvuuttssrrqqppoonnnmmmlllkk\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaaa\\ncccbb\\nccccc\\naaaa\\nbaaa\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaabbbbccccddddeeeeffffgggghhh\\nrrrqqqpppooonnnmmmlllkkkjjjiiih\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbccc\\nddddc\\nddddd\\naaaaaaaaaaaaaaaabbbbbbbbbbbbbbb\\ndddddddddddddddcccccccccccccccb\\n\", \"aaaabb\\nccccbb\\naaabb\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaaabb\\nccccbb\\naaaaa\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaaa\\naaaaaaaaa\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaaa\\naaaaaaaaa\\naaab\\ndccb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaaa\\naaaaaaaaa\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naaabb\\naaaaaaaaa\\naaaaaaaaa\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaab\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naabbc\\naaaaaaaaa\\naaaaaaaaa\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaaabb\\nccccbb\\naaabb\\naaaaaaaaa\\naaaaaaaaa\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\nbbbb\\nbbbb\\nbbbb\\naaaaa\\naaaaa\\nabbbb\\nbbbbb\\nbbbbb\\naabbccddeeffgghhiijjkkllmmnnoop\\nSRQPONMLKJIHGFEDCBAzyxwvutsrqqp\\n\", \"aaaaaa\\naaaaaa\\naabbc\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbbcc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\nbbbb\\ncccc\\ndddd\\ndddd\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaaa\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaaabbbbbbccccccddddddeeeeeef\\nkkkkkjjjjjiiiiihhhhhggggggfffff\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbbcc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naaaaa\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\nbbbb\\ncccc\\ndddd\\ndddd\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaaa\\naaabb\\nbbbbb\\nbbbcc\\nddddd\\neeeee\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naaaaa\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\naaaa\\nbbbb\\ncccc\\ndddd\\ndddd\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\naaaaa\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\", \"aaaabb\\nccccbb\\naaaaa\\naaaaaaaab\\nbbbbbbbbb\\naaab\\nccbb\\nddde\\neeee\\neffg\\nihhg\\nijjj\\na\\n\", \"aaabb\\ncccbb\\nccccc\\naaaa\\nbbba\\nbbcc\\ndddc\\neeee\\nffff\\naaabb\\nbbbbb\\nbcccc\\ndddcc\\nddddd\\nabcdefghijklmnopqrstuvwxyzABCDE\\n9876543210ZYXWVUTSRQPONMLKJIHGF\\n\"]}", "source": "taco"}
|
Long is a huge fan of CFC (Codeforces Fried Chicken). But the price of CFC is increasing, so he decides to breed the chicken on his own farm.
His farm is presented by a rectangle grid with r rows and c columns. Some of these cells contain rice, others are empty. k chickens are living on his farm. The number of chickens is not greater than the number of cells with rice on the farm.
Long wants to give his chicken playgrounds by assigning these farm cells to his chickens. He would like to satisfy the following requirements:
* Each cell of the farm is assigned to exactly one chicken.
* Each chicken is assigned at least one cell.
* The set of cells assigned to every chicken forms a connected area. More precisely, if two cells (x, y) and (u, v) are assigned to the same chicken, this chicken is able to walk from (x, y) to (u, v) by passing only its cells and moving from each cell to another cell sharing a side.
Long also wants to prevent his chickens from fighting for food. Hence he wants the difference between the maximum and the minimum number of cells with rice assigned to a chicken to be as small as possible. Please help him.
Input
Each test contains multiple test cases. The first line contains the number of test cases T (1 ≤ T ≤ 2 ⋅ 10^4). Description of the test cases follows.
The first line of each test case contains three integers r, c and k (1 ≤ r, c ≤ 100, 1 ≤ k ≤ 62), representing the size of Long's farm and the number of chickens Long has.
Each of the next r lines contains c characters, each is either "." or "R", representing an empty cell or a cell with rice. It is guaranteed that the number of chickens is not greater than the number of cells with rice on the farm.
It is guaranteed that the sum of r ⋅ c over all test cases does not exceed 2 ⋅ 10^4.
Output
For each test case, print r lines with c characters on each line. Each character should be either a lowercase English character, an uppercase English character, or a digit. Two characters should be equal if and only if the two corresponding cells are assigned to the same chicken. Uppercase and lowercase characters are considered different, so "A" and "a" belong to two different chickens.
If there are multiple optimal answers, print any.
Example
Input
4
3 5 3
..R..
...R.
....R
6 4 6
R..R
R..R
RRRR
RRRR
R..R
R..R
5 5 4
RRR..
R.R..
RRR..
R..R.
R...R
2 31 62
RRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR
RRRRRRRRRRRRRRRRRRRRRRRRRRRRRRR
Output
11122
22223
33333
aacc
aBBc
aBBc
CbbA
CbbA
CCAA
11114
22244
32444
33344
33334
abcdefghijklmnopqrstuvwxyzABCDE
FGHIJKLMNOPQRSTUVWXYZ0123456789
Note
These pictures explain the sample output. Each color represents one chicken. Cells filled with patterns (not solid colors) contain rice.
In the first test case, each chicken has one cell with rice. Hence, the difference between the maximum and the minimum number of cells with rice assigned to a chicken is 0.
<image>
In the second test case, there are 4 chickens with 3 cells of rice, and 2 chickens with 2 cells of rice. Hence, the difference between the maximum and the minimum number of cells with rice assigned to a chicken is 3 - 2 = 1.
<image>
In the third test case, each chicken has 3 cells with rice. <image>
In the last test case, since there are 62 chicken with exactly 62 cells of rice, each chicken must be assigned to exactly one cell. The sample output is one of the possible way.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [[1, 1], [2, 2], [2, 3], [2, 4], [3, 1], [3, 2], [3, 3], [3, 4], [3, 5], [4, 2], [4, 3], [4, 4], [4, 5], [4, 6], [5, 4], [5, 5], [5, 6], [100, 100]], \"outputs\": [[\"R\"], [\"L\"], [\"L\"], [\"L\"], [\"D\"], [\"U\"], [\"R\"], [\"R\"], [\"R\"], [\"U\"], [\"D\"], [\"L\"], [\"L\"], [\"L\"], [\"U\"], [\"R\"], [\"R\"], [\"L\"]]}", "source": "taco"}
|
# Task
You're standing at the top left corner of an `n × m` grid and facing towards the `right`.
Then you start walking one square at a time in the direction you are facing.
If you reach the border of the grid or if the next square you are about to visit has already been visited, you turn right.
You stop when all the squares in the grid are visited. What direction will you be facing when you stop?
You can see the example of your long walk in the image below. The numbers denote the order in which you visit the cells.
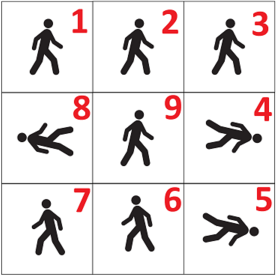
Given two integers n and m, denoting the number of rows and columns respectively, find out the direction you will be facing at the end.
Output `"L"` for left, `"R"` for right, `"U"` for up, and `"D"` for down.
# Example:
For `n = 3, m = 3`, the output should be `"R"`.
This example refers to the picture given in the description. At the end of your walk you will be standing in the middle of the grid facing right.
# Input/Output
- `[input]` integer `n`
number of rows.
`1 <= n <= 1000`
- `[input]` integer `m`
number of columns.
`1 <= m <= 1000`
- `[output]` a string
The final direction.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [\"4\\n3 6 28 9\\n\", \"5\\n5 12 9 16 48\\n\", \"4\\n1 2 4 8\\n\", \"1\\n1000000000000000000\\n\", \"4\\n70369817919488 281474976710657 70368744177665 281476050452480\\n\", \"5\\n292733975779082240 18014398509482240 306244774661193728 4504699138998272 1099511628032\\n\", \"30\\n550292684800 2149580800 4194320 576531121047601152 1125899906842628 577023702256844800 36028799166447616 584115552256 144115256795332608 1103806595072 70368811286528 278528 8830452760576 1125968626319360 2251800887427072 2097168 562958543355904 98304 9007200328482816 8590000128 2253998836940800 8800387989504 18691697672192 36028797018996736 4194308 17592186306560 537395200 9007199255265280 67125248 144117387099111424\\n\", \"35\\n1099511627784 36028797019488256 576460752303423490 17592186044672 18014398510006272 274877923328 2252899325313024 16777248 4297064448 4210688 17592454479872 4505798650626048 4503599627371520 612489549322387456 2251808403619840 1074790400 562958543355904 549756862464 562949953421440 8320 9007199523176448 8796093022464 8796093030400 2199040032768 70368744181760 4295098368 288230376151842816 18084767253659648 2097184 5120 9007474132647936 1077936128 514 288230925907525632 520\\n\", \"4\\n269019726702209410 974764215496813080 547920080673102148 403277729561219906\\n\", \"10\\n76578820211343624 0 293297008968192 0 0 0 189152283861189120 324294649604739072 20266198324215808 0\\n\", \"10\\n565299879350784 4508014854799360 0 0 0 4503635094929409 18014810826352646 306526525186934784 0 0\\n\", \"10\\n193953851215184128 21533387621925025 0 0 90143735963329536 2272071319648 0 0 3378250047292544 0\\n\", \"10\\n32832 0 154618822656 0 4311744512 12884901888 25769803776 16809984 137438953536 0\\n\", \"100\\n0 0 0 0 0 16896 0 0 0 393216 537919488 0 0 0 147456 1310720 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2251799813685312 0 0 0 0 105553116266496 0 0 576 3377699720527872 0 0 0 0 0 0 0 0 17867063951360 0 0 1196268651020288 0 0 0 0 146028888064 0 9126805504 0 0 0 0 0 0 0 0 412316860416 0 0 0 52776558133248 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"10\\n145135569469440 4415327043584 17247502464 72075186223972364 145241087982700608 144115188076380352 52776826568712 72198331527331844 46161896180549632 45071180914229248\\n\", \"20\\n144115188142973184 18015498289545217 9077576588853760 4573976961482880 144150509954007040 4295098374 290482175998952448 290486848889815040 393228 8796118192128 4672941199360 36029898946510848 18014467230007297 4503599627379072 33817608 36028803461414914 9007199389483520 149533589782528 140737623113728 35390531567616\\n\", \"20\\n0 0 554050781184 11258999068426240 141836999983104 1107296256 2251834173423616 9007199255789568 18014467228958720 4503633987108864 18155135997837312 4504149383184384 0 144123984168878080 34603008 1100585369600 8800387989504 0 144115256795332608 0\\n\", \"35\\n0 288230376151711748 276824064 288230444871188480 563499709235200 550024249344 36864 68719476992 160 0 0 0 0 0 0 0 0 2199023321088 33024 0 0 0 0 0 2814749767106560 0 34359738372 576460752370532352 0 69632 2199023271936 0 2251834173423616 75497472 576460752303439872\\n\", \"20\\n17592722915328 137438953728 0 549755822096 2251800350556160 70368744185856 0 2251804108652544 0 1099511628288 17592186045440 8864812498944 79164837199872 0 68719477760 1236950581248 549755814400 0 17179869456 21474836480\\n\", \"20\\n8589950976 0 8858370048 1342177280 65536 2199023255808 0 1075838976 0 35184372285440 0 0 0 9009398277996544 2228224 16640 0 9042383626829824 0 0\\n\", \"50\\n65600 17825792 0 288230376285929472 16392 0 0 16896 0 0 10486272 140737488355330 65537 171798691840 571746046443520 0 0 33024 0 2052 36028797155278848 36028805608898560 0 0 562967133290496 0 0 0 146028888064 281474976710660 0 288230376151711746 8388864 0 17180393472 0 0 0 68719476737 34376515584 0 299067162755072 68719478784 0 9007199255789568 140737488879616 9007199254773760 8796093022272 4294967304 17596481011712\\n\", \"35\\n274877906976 65544 8796361457664 288230376151712256 549755817984 36028797019095040 33556482 167772160 1099511635968 72057594037936128 524289 288230376151711776 18014398509482000 34363932672 1099511627840 18049582881570816 34359738384 108086391056891904 68719738880 2286984185774080 1073745920 68719476746 9007203549708288 2251799813816320 402653184 16842752 2112 786432 9007474132647936 4831838208 2097153 549755814400 1090519040 8796097216512 538968064\\n\", \"2\\n267367244641009858 102306300054748095\\n\", \"3\\n268193483524125986 538535259923264236 584613336374288890\\n\", \"5\\n269845965585325538 410993175365329220 287854792412106894 411389931291882088 384766635564718672\\n\", \"6\\n270672213058376258 847222126643910769 251161541005887447 196130104757703053 970176324544067925 590438340902981666\\n\", \"7\\n271498451941492386 506823119072235421 991096248449924897 204242310783332531 778958050378192987 384042493592684635 942496553147499871\\n\", \"8\\n272324690824608514 943052078940751562 954402997043705450 212354512513994712 364367743652509536 401018687432130708 606631724317463342 824875323687041818\\n\", \"9\\n273150934002691938 379281034514300406 694337708782710196 220466718539624190 949777432631858790 417994876976609485 494138923752268029 239707031030225806 400378607279200010\\n\", \"10\\n996517375802030517 559198117598196517 624045669640274070 717274415983359970 778062383071550120 624694462096204861 661230177799843966 796915526446173606 891967553796619137 158012341402690753\\n\", \"20\\n738505179452405439 393776795586588703 916949583509061480 942864257552472139 431031017016115809 547400344148658853 843639266066743033 751410499628305149 926196799677780683 288523782519361359 236550712208050515 88576472401554300 610164240954478789 948544811346543677 828908414387546137 615705220832279892 728861610641889898 318107398080960259 253426267717802880 526751456588066498\\n\", \"6\\n288793326105133056 160 9077567998918656 9007199254741024 562949953421440 288300744895889408\\n\", \"7\\n69206016 134250496 2149580800 2147516416 144115188142964736 146366987889541120 2251799947902976\\n\", \"8\\n90071992547409920 4503599627370500 18014398510006272 72057594037928192 260 525312 4503599627632640 263168\\n\", \"9\\n1161084278931456 1125899906843648 1140850688 274877972480 70643622084608 633318697598976 1073807360 35184439197696 562949953422336\\n\", \"10\\n289356276058554368 4503599627378688 72057594038059008 1126037345796096 288230376152760320 4503599627370498 139264 72057594038976512 70506183131136 70368744177666\\n\", \"12\\n2176 562967133290496 1073807360 17179871232 9011597301252096 4398046511168 9007267974217728 562949953421376 68719607808 35185445830656 196608 35184372088960\\n\", \"14\\n72058143793741824 144115325514809344 36028797018966016 144115188080050176 135168 1125899911036928 36028797019095040 412316860416 8796093024256 1126449662656512 8864812498944 72057662757404672 274877906952 4104\\n\", \"18\\n277025390592 9007199254773760 140737488371712 72057594037944320 288230378299195392 140737555464192 2199024304128 576460752303427584 201326592 1048608 137439477760 2199023779840 4128 648518346341351424 141733920768 297237575406452736 275012124672 4295000064\\n\", \"25\\n4398046511360 562949957615616 17179885568 70403103916032 4398048608256 262152 5242880 281474976710657 268435968 72057594037928064 8796093022209 1048704 633318697598976 72057611217797120 171798691840 35184372089088 40960 8796093153280 163840 137438953480 281474976711168 270336 2251799815782400 2251800082120704 35184372105216\\n\", \"20\\n0 0 2148564992 20301391285223424 0 2260595906773568 0 637721039077904 0 72058143793742848 0 0 0 288230376151711776 0 0 4299169792 0 9147936743096322 36046457941262624\\n\", \"40\\n0 0 0 0 33554432 0 0 34359738376 0 0 0 0 0 0 0 0 16392 598169893278720 0 0 288230651029686272 0 0 0 0 0 299084343836800 0 2287052905529600 0 0 0 0 0 0 0 28217866417348608 4311744576 0 558630961281\\n\", \"100\\n0 0 0 0 0 0 0 0 0 70368744472576 0 0 0 0 0 0 0 0 0 0 0 144678138029342720 0 0 0 0 0 281474977767489 0 16783360 0 0 0 0 0 288793463544086528 0 0 0 0 0 0 0 0 0 18144089473024 20 0 0 0 0 0 0 0 0 0 0 0 0 144115222435725440 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 18014419984875520 0 0 0 0 0 0 0 0 0 274878432256 0 0 0 38280596899758080 0 0 0 0 0 0 0 18014398509813764 72057594046316576 0\\n\", \"100\\n0 0 0 72057598886543392 0 0 0 0 0 0 34635777 0 0 0 0 0 0 0 0 0 0 145276272354791568 0 0 0 0 0 0 0 268435456 0 0 0 299068236759040 0 0 2251800082128928 1236950844416 0 0 0 0 0 0 0 0 290482175998951428 0 0 0 2621440 0 0 0 0 0 0 0 0 0 0 0 4259840 0 0 0 0 0 4398046511108 0 0 0 0 0 0 288230376151712258 0 144258124587466816 0 0 0 0 0 0 0 0 0 0 0 0 1266637395206144 0 281818574094336 0 0 0 0 0 0 0\\n\", \"150\\n0 0 0 0 0 0 0 2537672836907008 0 0 0 0 0 0 16384 0 0 0 0 34360787232 0 0 70871155232 0 0 0 0 0 0 0 0 0 0 0 2256197860262016 0 0 0 0 0 0 0 0 0 0 536872961 0 0 0 0 0 0 0 0 0 0 33619968 0 0 0 0 0 0 0 0 0 0 0 0 37189881297899520 0 18031990695526400 0 0 1099511627776 0 0 0 0 0 0 0 0 2097152 0 0 0 134217984 0 0 0 0 0 0 32768 0 0 0 0 0 0 0 0 72057594037928066 0 0 0 0 297307996227110981 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 288240271756361736 0 2097154 0 9007199254740992 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"10\\n70377334112256 2304 134219776 0 8724152320 70368744177920 0 0 0 0\\n\", \"15\\n4296097792 1125934333693952 288230376152777216 68719509522 1126484559265792 140737756799040 18155136283049984 36028797052551170 288300753485824512 4299227392 70377334120512 18023194619281412 36028797056712960 8796160135172 619012161552\\n\", \"20\\n67109888 0 0 67108896 562949953422336 0 68719480832 134217760 562949954469888 0 36028797153181696 0 36028865738440704 0 0 0 4098 1048578 0 0\\n\", \"50\\n72057594038452224 0 12884901888 288230376151713792 65664 0 0 0 0 17314086912 150994944 0 18031990695526400 580964351930793984 72066390130950144 17179871232 17592186060800 0 35184372088848 4297064448 0 24 0 0 576460753377165312 8589934593 0 0 0 549755879424 562949953437696 175921860444160 553648128 4504149383184384 0 0 274877906952 0 0 0 0 0 562949953454080 1125899906842752 140738562097152 537395200 288230376153808896 1134695999864832 32769 18014673387388928\\n\", \"35\\n18049582881570816 2112 0 2251799813816320 108086391056891904 0 2 0 0 0 402653184 2286984185774080 0 0 0 0 0 0 68719738880 0 72057594037936128 33556482 34359738384 0 0 1099511627840 0 167772160 18014398509482000 34363932672 8796361457664 36028797019095040 1099511635968 0 8796097216512\\n\", \"20\\n137438953728 288230384741646336 17592186045440 1125908496777232 1236950581248 17592722915328 8864812498944 1099511628288 79164837199872 144115188075855876 17179869440 2251804108652544 2251800350556160 68719477760 21474836480 288230376151711748 145241087982698496 70368744185856 549755822096 549755814400\\n\", \"20\\n281474976710658 1075838976 281477124194304 2147487744 35184372285440 8196 2228224 4112 9042383626829824 275012190208 1342177280 8858370048 8589950976 1125899906850816 274877906960 6 2199023255808 1125900041060352 9009398277996544 16640\\n\", \"3\\n1 1 3\\n\", \"7\\n5 42 80 192 160 9 22\\n\", \"7\\n129 259 6 12 24 304 224\\n\", \"3\\n5 5 5\\n\", \"5\\n25 3 44 6 48\\n\", \"5\\n49 3 6 44 24\\n\", \"6\\n97 3 6 28 40 80\\n\", \"5\\n25 48 3 6 44\\n\", \"7\\n641 1283 2054 4108 8216 16688 32992\\n\", \"7\\n259 6 12 24 304 224 129\\n\", \"179\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\\n\", \"27\\n4295000064 274877906976 48389226512 33554434 68720525312 4194320 67108865 96 2056 413264846980 541065216 17179901952 8589935104 129 2147487744 68719607808 139586437120 17315009610 1280 2097408 25165824 1107296256 268435968 278528 34376515584 16388 10240\\n\", \"150\\n0 0 0 0 0 0 0 2537672836907008 0 0 0 0 0 0 16384 0 0 0 0 34360787232 0 0 70871155232 0 0 0 0 0 0 0 0 0 0 0 2256197860262016 0 0 0 0 0 0 0 0 0 0 536872961 0 0 0 0 0 0 0 0 0 0 33619968 0 0 0 0 0 0 0 0 0 0 0 0 37189881297899520 0 18031990695526400 0 0 1099511627776 0 0 0 0 0 0 0 0 2097152 0 0 0 134217984 0 0 0 0 0 0 32768 0 0 0 0 0 0 0 0 72057594037928066 0 0 0 0 297307996227110981 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 288240271756361736 0 2097154 0 9007199254740992 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"12\\n2176 562967133290496 1073807360 17179871232 9011597301252096 4398046511168 9007267974217728 562949953421376 68719607808 35185445830656 196608 35184372088960\\n\", \"5\\n292733975779082240 18014398509482240 306244774661193728 4504699138998272 1099511628032\\n\", \"10\\n145135569469440 4415327043584 17247502464 72075186223972364 145241087982700608 144115188076380352 52776826568712 72198331527331844 46161896180549632 45071180914229248\\n\", \"7\\n5 42 80 192 160 9 22\\n\", \"8\\n272324690824608514 943052078940751562 954402997043705450 212354512513994712 364367743652509536 401018687432130708 606631724317463342 824875323687041818\\n\", \"10\\n193953851215184128 21533387621925025 0 0 90143735963329536 2272071319648 0 0 3378250047292544 0\\n\", \"20\\n8589950976 0 8858370048 1342177280 65536 2199023255808 0 1075838976 0 35184372285440 0 0 0 9009398277996544 2228224 16640 0 9042383626829824 0 0\\n\", \"35\\n274877906976 65544 8796361457664 288230376151712256 549755817984 36028797019095040 33556482 167772160 1099511635968 72057594037936128 524289 288230376151711776 18014398509482000 34363932672 1099511627840 18049582881570816 34359738384 108086391056891904 68719738880 2286984185774080 1073745920 68719476746 9007203549708288 2251799813816320 402653184 16842752 2112 786432 9007474132647936 4831838208 2097153 549755814400 1090519040 8796097216512 538968064\\n\", \"35\\n1099511627784 36028797019488256 576460752303423490 17592186044672 18014398510006272 274877923328 2252899325313024 16777248 4297064448 4210688 17592454479872 4505798650626048 4503599627371520 612489549322387456 2251808403619840 1074790400 562958543355904 549756862464 562949953421440 8320 9007199523176448 8796093022464 8796093030400 2199040032768 70368744181760 4295098368 288230376151842816 18084767253659648 2097184 5120 9007474132647936 1077936128 514 288230925907525632 520\\n\", \"50\\n65600 17825792 0 288230376285929472 16392 0 0 16896 0 0 10486272 140737488355330 65537 171798691840 571746046443520 0 0 33024 0 2052 36028797155278848 36028805608898560 0 0 562967133290496 0 0 0 146028888064 281474976710660 0 288230376151711746 8388864 0 17180393472 0 0 0 68719476737 34376515584 0 299067162755072 68719478784 0 9007199255789568 140737488879616 9007199254773760 8796093022272 4294967304 17596481011712\\n\", \"3\\n1 1 3\\n\", \"20\\n0 0 2148564992 20301391285223424 0 2260595906773568 0 637721039077904 0 72058143793742848 0 0 0 288230376151711776 0 0 4299169792 0 9147936743096322 36046457941262624\\n\", \"7\\n641 1283 2054 4108 8216 16688 32992\\n\", \"6\\n288793326105133056 160 9077567998918656 9007199254741024 562949953421440 288300744895889408\\n\", \"10\\n996517375802030517 559198117598196517 624045669640274070 717274415983359970 778062383071550120 624694462096204861 661230177799843966 796915526446173606 891967553796619137 158012341402690753\\n\", \"50\\n72057594038452224 0 12884901888 288230376151713792 65664 0 0 0 0 17314086912 150994944 0 18031990695526400 580964351930793984 72066390130950144 17179871232 17592186060800 0 35184372088848 4297064448 0 24 0 0 576460753377165312 8589934593 0 0 0 549755879424 562949953437696 175921860444160 553648128 4504149383184384 0 0 274877906952 0 0 0 0 0 562949953454080 1125899906842752 140738562097152 537395200 288230376153808896 1134695999864832 32769 18014673387388928\\n\", \"100\\n0 0 0 72057598886543392 0 0 0 0 0 0 34635777 0 0 0 0 0 0 0 0 0 0 145276272354791568 0 0 0 0 0 0 0 268435456 0 0 0 299068236759040 0 0 2251800082128928 1236950844416 0 0 0 0 0 0 0 0 290482175998951428 0 0 0 2621440 0 0 0 0 0 0 0 0 0 0 0 4259840 0 0 0 0 0 4398046511108 0 0 0 0 0 0 288230376151712258 0 144258124587466816 0 0 0 0 0 0 0 0 0 0 0 0 1266637395206144 0 281818574094336 0 0 0 0 0 0 0\\n\", \"9\\n273150934002691938 379281034514300406 694337708782710196 220466718539624190 949777432631858790 417994876976609485 494138923752268029 239707031030225806 400378607279200010\\n\", \"10\\n70377334112256 2304 134219776 0 8724152320 70368744177920 0 0 0 0\\n\", \"10\\n289356276058554368 4503599627378688 72057594038059008 1126037345796096 288230376152760320 4503599627370498 139264 72057594038976512 70506183131136 70368744177666\\n\", \"100\\n0 0 0 0 0 0 0 0 0 70368744472576 0 0 0 0 0 0 0 0 0 0 0 144678138029342720 0 0 0 0 0 281474977767489 0 16783360 0 0 0 0 0 288793463544086528 0 0 0 0 0 0 0 0 0 18144089473024 20 0 0 0 0 0 0 0 0 0 0 0 0 144115222435725440 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 18014419984875520 0 0 0 0 0 0 0 0 0 274878432256 0 0 0 38280596899758080 0 0 0 0 0 0 0 18014398509813764 72057594046316576 0\\n\", \"15\\n4296097792 1125934333693952 288230376152777216 68719509522 1126484559265792 140737756799040 18155136283049984 36028797052551170 288300753485824512 4299227392 70377334120512 18023194619281412 36028797056712960 8796160135172 619012161552\\n\", \"8\\n90071992547409920 4503599627370500 18014398510006272 72057594037928192 260 525312 4503599627632640 263168\\n\", \"35\\n0 288230376151711748 276824064 288230444871188480 563499709235200 550024249344 36864 68719476992 160 0 0 0 0 0 0 0 0 2199023321088 33024 0 0 0 0 0 2814749767106560 0 34359738372 576460752370532352 0 69632 2199023271936 0 2251834173423616 75497472 576460752303439872\\n\", \"20\\n0 0 554050781184 11258999068426240 141836999983104 1107296256 2251834173423616 9007199255789568 18014467228958720 4503633987108864 18155135997837312 4504149383184384 0 144123984168878080 34603008 1100585369600 8800387989504 0 144115256795332608 0\\n\", \"20\\n137438953728 288230384741646336 17592186045440 1125908496777232 1236950581248 17592722915328 8864812498944 1099511628288 79164837199872 144115188075855876 17179869440 2251804108652544 2251800350556160 68719477760 21474836480 288230376151711748 145241087982698496 70368744185856 549755822096 549755814400\\n\", \"20\\n144115188142973184 18015498289545217 9077576588853760 4573976961482880 144150509954007040 4295098374 290482175998952448 290486848889815040 393228 8796118192128 4672941199360 36029898946510848 18014467230007297 4503599627379072 33817608 36028803461414914 9007199389483520 149533589782528 140737623113728 35390531567616\\n\", \"14\\n72058143793741824 144115325514809344 36028797018966016 144115188080050176 135168 1125899911036928 36028797019095040 412316860416 8796093024256 1126449662656512 8864812498944 72057662757404672 274877906952 4104\\n\", \"20\\n67109888 0 0 67108896 562949953422336 0 68719480832 134217760 562949954469888 0 36028797153181696 0 36028865738440704 0 0 0 4098 1048578 0 0\\n\", \"5\\n49 3 6 44 24\\n\", \"10\\n76578820211343624 0 293297008968192 0 0 0 189152283861189120 324294649604739072 20266198324215808 0\\n\", \"25\\n4398046511360 562949957615616 17179885568 70403103916032 4398048608256 262152 5242880 281474976710657 268435968 72057594037928064 8796093022209 1048704 633318697598976 72057611217797120 171798691840 35184372089088 40960 8796093153280 163840 137438953480 281474976711168 270336 2251799815782400 2251800082120704 35184372105216\\n\", \"6\\n270672213058376258 847222126643910769 251161541005887447 196130104757703053 970176324544067925 590438340902981666\\n\", \"30\\n550292684800 2149580800 4194320 576531121047601152 1125899906842628 577023702256844800 36028799166447616 584115552256 144115256795332608 1103806595072 70368811286528 278528 8830452760576 1125968626319360 2251800887427072 2097168 562958543355904 98304 9007200328482816 8590000128 2253998836940800 8800387989504 18691697672192 36028797018996736 4194308 17592186306560 537395200 9007199255265280 67125248 144117387099111424\\n\", \"20\\n17592722915328 137438953728 0 549755822096 2251800350556160 70368744185856 0 2251804108652544 0 1099511628288 17592186045440 8864812498944 79164837199872 0 68719477760 1236950581248 549755814400 0 17179869456 21474836480\\n\", \"7\\n271498451941492386 506823119072235421 991096248449924897 204242310783332531 778958050378192987 384042493592684635 942496553147499871\\n\", \"1\\n1000000000000000000\\n\", \"20\\n738505179452405439 393776795586588703 916949583509061480 942864257552472139 431031017016115809 547400344148658853 843639266066743033 751410499628305149 926196799677780683 288523782519361359 236550712208050515 88576472401554300 610164240954478789 948544811346543677 828908414387546137 615705220832279892 728861610641889898 318107398080960259 253426267717802880 526751456588066498\\n\", \"7\\n129 259 6 12 24 304 224\\n\", \"7\\n259 6 12 24 304 224 129\\n\", \"7\\n69206016 134250496 2149580800 2147516416 144115188142964736 146366987889541120 2251799947902976\\n\", \"35\\n18049582881570816 2112 0 2251799813816320 108086391056891904 0 2 0 0 0 402653184 2286984185774080 0 0 0 0 0 0 68719738880 0 72057594037936128 33556482 34359738384 0 0 1099511627840 0 167772160 18014398509482000 34363932672 8796361457664 36028797019095040 1099511635968 0 8796097216512\\n\", \"100\\n0 0 0 0 0 16896 0 0 0 393216 537919488 0 0 0 147456 1310720 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2251799813685312 0 0 0 0 105553116266496 0 0 576 3377699720527872 0 0 0 0 0 0 0 0 17867063951360 0 0 1196268651020288 0 0 0 0 146028888064 0 9126805504 0 0 0 0 0 0 0 0 412316860416 0 0 0 52776558133248 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"40\\n0 0 0 0 33554432 0 0 34359738376 0 0 0 0 0 0 0 0 16392 598169893278720 0 0 288230651029686272 0 0 0 0 0 299084343836800 0 2287052905529600 0 0 0 0 0 0 0 28217866417348608 4311744576 0 558630961281\\n\", \"4\\n70369817919488 281474976710657 70368744177665 281476050452480\\n\", \"5\\n25 48 3 6 44\\n\", \"5\\n269845965585325538 410993175365329220 287854792412106894 411389931291882088 384766635564718672\\n\", \"4\\n269019726702209410 974764215496813080 547920080673102148 403277729561219906\\n\", \"18\\n277025390592 9007199254773760 140737488371712 72057594037944320 288230378299195392 140737555464192 2199024304128 576460752303427584 201326592 1048608 137439477760 2199023779840 4128 648518346341351424 141733920768 297237575406452736 275012124672 4295000064\\n\", \"3\\n5 5 5\\n\", \"179\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\\n\", \"5\\n25 3 44 6 48\\n\", \"10\\n565299879350784 4508014854799360 0 0 0 4503635094929409 18014810826352646 306526525186934784 0 0\\n\", \"20\\n281474976710658 1075838976 281477124194304 2147487744 35184372285440 8196 2228224 4112 9042383626829824 275012190208 1342177280 8858370048 8589950976 1125899906850816 274877906960 6 2199023255808 1125900041060352 9009398277996544 16640\\n\", \"9\\n1161084278931456 1125899906843648 1140850688 274877972480 70643622084608 633318697598976 1073807360 35184439197696 562949953422336\\n\", \"6\\n97 3 6 28 40 80\\n\", \"2\\n267367244641009858 102306300054748095\\n\", \"27\\n4295000064 274877906976 48389226512 33554434 68720525312 4194320 67108865 96 2056 413264846980 541065216 17179901952 8589935104 129 2147487744 68719607808 139586437120 17315009610 1280 2097408 25165824 1107296256 268435968 278528 34376515584 16388 10240\\n\", \"10\\n32832 0 154618822656 0 4311744512 12884901888 25769803776 16809984 137438953536 0\\n\", \"3\\n268193483524125986 538535259923264236 584613336374288890\\n\", \"150\\n0 0 0 0 0 0 0 2537672836907008 0 0 0 0 0 0 16384 0 0 0 0 34360787232 0 0 70871155232 0 0 0 0 0 0 0 0 0 0 0 2256197860262016 0 0 0 0 0 0 0 0 0 0 536872961 0 0 0 0 0 0 0 0 0 0 33619968 0 0 0 0 0 0 0 0 0 0 0 0 37189881297899520 0 18031990695526400 0 0 1099511627776 0 0 0 0 0 0 0 0 2097152 0 0 0 134217984 0 0 0 0 0 0 32768 0 0 0 0 0 0 0 0 72057594037928066 0 0 0 0 356987788379886167 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 288240271756361736 0 2097154 0 9007199254740992 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"3\\n2 1 3\\n\", \"35\\n0 288230376151711748 276824064 288230444871188480 563499709235200 550024249344 36864 68719476992 160 0 0 0 0 0 0 0 0 2199023321088 33024 0 0 0 0 0 2814749767106560 0 34359738372 576460752370532352 0 69632 2199023271936 1 2251834173423616 75497472 576460752303439872\\n\", \"100\\n0 0 0 0 0 16896 0 0 0 393216 537919488 0 0 0 147456 1310720 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2251799813685312 0 0 0 0 105553116266496 0 0 576 3377699720527872 0 0 0 0 0 0 0 0 17867063951360 0 0 1196268651020288 0 0 0 0 146028888064 0 9126805504 0 0 0 0 0 0 0 0 412316860416 0 0 0 52776558133248 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"12\\n2176 562967133290496 1073807360 17179871232 9011597301252096 4398046511168 9007267974217728 562949953421376 68719607808 35185445830656 196608 724420969840\\n\", \"5\\n292733975779082240 18014398509482240 495419805615879253 4504699138998272 1099511628032\\n\", \"10\\n145135569469440 4415327043584 6163023619 72075186223972364 145241087982700608 144115188076380352 52776826568712 72198331527331844 46161896180549632 45071180914229248\\n\", \"7\\n5 42 80 170 160 9 22\\n\", \"8\\n516839298071550157 943052078940751562 954402997043705450 212354512513994712 364367743652509536 401018687432130708 606631724317463342 824875323687041818\\n\", \"10\\n19635690084315929 21533387621925025 0 0 90143735963329536 2272071319648 0 0 3378250047292544 0\\n\", \"35\\n274877906976 38566 8796361457664 288230376151712256 549755817984 36028797019095040 33556482 167772160 1099511635968 72057594037936128 524289 288230376151711776 18014398509482000 34363932672 1099511627840 18049582881570816 34359738384 108086391056891904 68719738880 2286984185774080 1073745920 68719476746 9007203549708288 2251799813816320 402653184 16842752 2112 786432 9007474132647936 4831838208 2097153 549755814400 1090519040 8796097216512 538968064\\n\", \"35\\n1099511627784 36028797019488256 576460752303423490 17592186044672 18014398510006272 274877923328 2252899325313024 16777248 4297064448 4210688 17592454479872 4505798650626048 4503599627371520 612489549322387456 2251808403619840 1074790400 562958543355904 549756862464 562949953421440 8320 9007199523176448 8796093022464 8796093030400 2199040032768 70368744181760 4295098368 288230376151842816 18084767253659648 2097184 5120 9007474132647936 1077936128 902 288230925907525632 520\\n\", \"50\\n65600 17825792 0 288230376285929472 16392 0 0 16896 0 0 10486272 140737488355330 65537 171798691840 571746046443520 0 0 33024 0 827 36028797155278848 36028805608898560 0 0 562967133290496 0 0 0 146028888064 281474976710660 0 288230376151711746 8388864 0 17180393472 0 0 0 68719476737 34376515584 0 299067162755072 68719478784 0 9007199255789568 140737488879616 9007199254773760 8796093022272 4294967304 17596481011712\\n\", \"20\\n0 0 2148564992 20301391285223424 0 2260595906773568 0 520918939168060 0 72058143793742848 0 0 0 288230376151711776 0 0 4299169792 0 9147936743096322 36046457941262624\\n\", \"7\\n641 1283 2054 4108 8216 16688 56724\\n\", \"6\\n288793326105133056 160 10915169159452971 9007199254741024 562949953421440 288300744895889408\\n\", \"10\\n996517375802030517 496087104143837434 624045669640274070 717274415983359970 778062383071550120 624694462096204861 661230177799843966 796915526446173606 891967553796619137 158012341402690753\\n\", \"50\\n72057594038452224 0 12884901888 288230376151713792 65664 0 0 0 0 17314086912 150994944 0 18031990695526400 580964351930793984 72066390130950144 17179871232 17592186060800 0 35184372088848 4297064448 0 24 0 0 576460753377165312 8589934593 0 0 0 751982377830 562949953437696 175921860444160 553648128 4504149383184384 0 0 274877906952 0 0 0 0 0 562949953454080 1125899906842752 140738562097152 537395200 288230376153808896 1134695999864832 32769 18014673387388928\\n\", \"100\\n0 0 0 72057598886543392 0 0 0 0 0 0 34635777 0 0 0 0 0 0 0 0 0 0 242739001344989705 0 0 0 0 0 0 0 268435456 0 0 0 299068236759040 0 0 2251800082128928 1236950844416 0 0 0 0 0 0 0 0 290482175998951428 0 0 0 2621440 0 0 0 0 0 0 0 0 0 0 0 4259840 0 0 0 0 0 4398046511108 0 0 0 0 0 0 288230376151712258 0 144258124587466816 0 0 0 0 0 0 0 0 0 0 0 0 1266637395206144 0 281818574094336 0 0 0 0 0 0 0\\n\", \"10\\n70377334112256 1296 134219776 0 8724152320 70368744177920 0 0 0 0\\n\", \"10\\n289356276058554368 1537201854073238 72057594038059008 1126037345796096 288230376152760320 4503599627370498 139264 72057594038976512 70506183131136 70368744177666\\n\", \"15\\n4296097792 1125934333693952 288230376152777216 68719509522 1126484559265792 140737756799040 18155136283049984 36028797052551170 288300753485824512 7779830379 70377334120512 18023194619281412 36028797056712960 8796160135172 619012161552\\n\", \"8\\n90071992547409920 4503599627370500 26142100925434208 72057594037928192 260 525312 4503599627632640 263168\\n\", \"20\\n0 0 242438878051 11258999068426240 141836999983104 1107296256 2251834173423616 9007199255789568 18014467228958720 4503633987108864 18155135997837312 4504149383184384 0 144123984168878080 34603008 1100585369600 8800387989504 0 144115256795332608 0\\n\", \"20\\n137438953728 106472963678046517 17592186045440 1125908496777232 1236950581248 17592722915328 8864812498944 1099511628288 79164837199872 144115188075855876 17179869440 2251804108652544 2251800350556160 68719477760 21474836480 288230376151711748 145241087982698496 70368744185856 549755822096 549755814400\\n\", \"20\\n144115188142973184 18015498289545217 9077576588853760 4573976961482880 144150509954007040 4295098374 290482175998952448 290486848889815040 393228 8796118192128 4672941199360 36029898946510848 18014467230007297 4503599627379072 7491843 36028803461414914 9007199389483520 149533589782528 140737623113728 35390531567616\\n\", \"14\\n72058143793741824 144115325514809344 36028797018966016 144115188080050176 135168 1445444739972716 36028797019095040 412316860416 8796093024256 1126449662656512 8864812498944 72057662757404672 274877906952 4104\\n\", \"5\\n49 3 12 44 24\\n\", \"10\\n76578820211343624 1 293297008968192 0 0 0 189152283861189120 324294649604739072 20266198324215808 0\\n\", \"25\\n4398046511360 66229806246628 17179885568 70403103916032 4398048608256 262152 5242880 281474976710657 268435968 72057594037928064 8796093022209 1048704 633318697598976 72057611217797120 171798691840 35184372089088 40960 8796093153280 163840 137438953480 281474976711168 270336 2251799815782400 2251800082120704 35184372105216\\n\", \"30\\n550292684800 2149580800 4194320 576531121047601152 1125899906842628 577023702256844800 36028799166447616 584115552256 144115256795332608 1103806595072 70368811286528 278528 8830452760576 1125968626319360 2251800887427072 2097168 562958543355904 98304 9007200328482816 8590000128 2253998836940800 8800387989504 18691697672192 36028797018996736 4194308 17592186306560 537395200 16974149152867780 67125248 144117387099111424\\n\", \"20\\n17592722915328 137438953728 0 615184025916 2251800350556160 70368744185856 0 2251804108652544 0 1099511628288 17592186045440 8864812498944 79164837199872 0 68719477760 1236950581248 549755814400 0 17179869456 21474836480\\n\", \"7\\n22376748927971712 506823119072235421 991096248449924897 204242310783332531 778958050378192987 384042493592684635 942496553147499871\\n\", \"1\\n1000000000000010000\\n\", \"20\\n738505179452405439 393776795586588703 916949583509061480 942864257552472139 431031017016115809 547400344148658853 48097136074838439 751410499628305149 926196799677780683 288523782519361359 236550712208050515 88576472401554300 610164240954478789 948544811346543677 828908414387546137 615705220832279892 728861610641889898 318107398080960259 253426267717802880 526751456588066498\\n\", \"7\\n129 259 12 12 24 304 224\\n\", \"7\\n259 6 12 24 304 224 238\\n\", \"7\\n69206016 134250496 2149580800 2147516416 7667730907514109 146366987889541120 2251799947902976\\n\", \"4\\n70369817919488 176875331485643 70368744177665 281476050452480\\n\", \"5\\n25 68 3 6 44\\n\", \"5\\n269845965585325538 113803390597162361 287854792412106894 411389931291882088 384766635564718672\\n\", \"4\\n269019726702209410 974764215496813080 547920080673102148 347348327742679698\\n\", \"18\\n277025390592 9007199254773760 267499925781328 72057594037944320 288230378299195392 140737555464192 2199024304128 576460752303427584 201326592 1048608 137439477760 2199023779840 4128 648518346341351424 141733920768 297237575406452736 275012124672 4295000064\\n\", \"3\\n4 5 5\\n\", \"179\\n1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1\\n\", \"5\\n21 3 44 6 48\\n\", \"20\\n281474976710658 1075838976 281477124194304 2147487744 35184372285440 8196 2228224 4112 9042383626829824 275012190208 1342177280 8858370048 8589950976 2047209679532165 274877906960 6 2199023255808 1125900041060352 9009398277996544 16640\\n\", \"9\\n1161084278931456 1125899906843648 1140850688 274877972480 134128193187324 633318697598976 1073807360 35184439197696 562949953422336\\n\", \"6\\n97 3 6 15 40 80\\n\", \"2\\n267367244641009858 123162617486314877\\n\", \"27\\n4295000064 274877906976 48389226512 33554434 68720525312 4194320 67108865 96 1452 413264846980 541065216 17179901952 8589935104 129 2147487744 68719607808 139586437120 17315009610 1280 2097408 25165824 1107296256 268435968 278528 34376515584 16388 10240\\n\", \"10\\n53665 0 154618822656 0 4311744512 12884901888 25769803776 16809984 137438953536 0\\n\", \"3\\n38552438220640338 538535259923264236 584613336374288890\\n\", \"4\\n2 2 4 8\\n\", \"5\\n5 10 9 16 48\\n\", \"4\\n3 6 28 3\\n\", \"150\\n0 0 0 0 0 0 0 2537672836907008 0 0 0 0 0 0 16384 0 0 0 0 34360787232 0 0 70871155232 0 0 0 0 0 0 0 0 0 0 0 2256197860262016 0 0 0 0 0 0 0 0 0 0 536872961 0 1 0 0 0 0 0 0 0 0 33619968 0 0 0 0 0 0 0 0 0 0 0 0 37189881297899520 0 18031990695526400 0 0 1099511627776 0 0 0 0 0 0 0 0 2097152 0 0 0 134217984 0 0 0 0 0 0 32768 0 0 0 0 0 0 0 0 72057594037928066 0 0 0 0 356987788379886167 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 288240271756361736 0 2097154 0 9007199254740992 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0\\n\", \"12\\n2176 562967133290496 1073807360 17179871232 9011597301252096 4398046511168 9007267974217728 562949953421376 68719607808 35185445830656 196608 1032870043623\\n\", \"5\\n292733975779082240 18014398509482240 495419805615879253 6819598634843768 1099511628032\\n\", \"10\\n145135569469440 3783930319586 6163023619 72075186223972364 145241087982700608 144115188076380352 52776826568712 72198331527331844 46161896180549632 45071180914229248\\n\", \"7\\n5 50 80 170 160 9 22\\n\", \"8\\n516839298071550157 943052078940751562 954402997043705450 212354512513994712 364367743652509536 383720167118521466 606631724317463342 824875323687041818\\n\", \"10\\n19635690084315929 21533387621925025 0 0 90143735963329536 2272071319648 1 0 3378250047292544 0\\n\", \"35\\n274877906976 38566 8796361457664 288230376151712256 549755817984 36028797019095040 33556482 167772160 1099511635968 72057594037936128 524289 288230376151711776 8946394069357714 34363932672 1099511627840 18049582881570816 34359738384 108086391056891904 68719738880 2286984185774080 1073745920 68719476746 9007203549708288 2251799813816320 402653184 16842752 2112 786432 9007474132647936 4831838208 2097153 549755814400 1090519040 8796097216512 538968064\\n\", \"35\\n1099511627784 36028797019488256 576460752303423490 17592186044672 18014398510006272 274877923328 2252899325313024 16777248 4297064448 4210688 17592454479872 4505798650626048 4503599627371520 642313302597715910 2251808403619840 1074790400 562958543355904 549756862464 562949953421440 8320 9007199523176448 8796093022464 8796093030400 2199040032768 70368744181760 4295098368 288230376151842816 18084767253659648 2097184 5120 9007474132647936 1077936128 902 288230925907525632 520\\n\", \"3\\n2 2 3\\n\", \"20\\n0 0 2148564992 20301391285223424 0 2260595906773568 0 520918939168060 0 72058143793742848 0 0 0 229658383091430906 0 0 4299169792 0 9147936743096322 36046457941262624\\n\", \"7\\n641 1283 2054 4108 8216 18673 56724\\n\", \"6\\n288793326105133056 251 10915169159452971 9007199254741024 562949953421440 288300744895889408\\n\", \"10\\n996517375802030517 496087104143837434 624045669640274070 717274415983359970 778062383071550120 624694462096204861 661230177799843966 9370792072762596 891967553796619137 158012341402690753\\n\", \"10\\n70377334112256 246 134219776 0 8724152320 70368744177920 0 0 0 0\\n\", \"10\\n13691061171404770 1537201854073238 72057594038059008 1126037345796096 288230376152760320 4503599627370498 139264 72057594038976512 70506183131136 70368744177666\\n\", \"15\\n4296097792 1125934333693952 288230376152777216 68719509522 1126484559265792 140737756799040 18155136283049984 36028797052551170 288300753485824512 7779830379 70377334120512 18023194619281412 5670903518711043 8796160135172 619012161552\\n\", \"8\\n90071992547409920 4503599627370500 26142100925434208 72057594037928192 457 525312 4503599627632640 263168\\n\", \"35\\n0 288230376151711748 276824064 288230444871188480 563499709235200 550024249344 36864 68719476992 160 0 1 0 0 0 0 0 0 2199023321088 33024 0 0 0 0 0 2814749767106560 0 34359738372 576460752370532352 0 69632 2199023271936 1 2251834173423616 75497472 576460752303439872\\n\", \"20\\n0 0 242438878051 11258999068426240 141836999983104 1107296256 2251834173423616 9007199255789568 18014467228958720 4503633987108864 18155135997837312 4504149383184384 0 144123984168878080 34603008 1100585369600 9518823146956 0 144115256795332608 0\\n\", \"20\\n137438953728 106472963678046517 17592186045440 1125908496777232 1236950581248 17592722915328 8864812498944 1099511628288 79164837199872 144115188075855876 16876546907 2251804108652544 2251800350556160 68719477760 21474836480 288230376151711748 145241087982698496 70368744185856 549755822096 549755814400\\n\", \"20\\n144115188142973184 18015498289545217 9077576588853760 4573976961482880 132235495042426052 4295098374 290482175998952448 290486848889815040 393228 8796118192128 4672941199360 36029898946510848 18014467230007297 4503599627379072 7491843 36028803461414914 9007199389483520 149533589782528 140737623113728 35390531567616\\n\", \"14\\n72058143793741824 144115325514809344 36028797018966016 144115188080050176 135168 1445444739972716 36028797019095040 412316860416 8796093024256 1126449662656512 8864812498944 72057662757404672 452502832419 4104\\n\", \"5\\n49 3 12 58 24\\n\", \"10\\n76578820211343624 1 293297008968192 0 0 0 189152283861189120 324294649604739072 20266198324215808 1\\n\", \"4\\n1 2 4 8\\n\", \"5\\n5 12 9 16 48\\n\", \"4\\n3 6 28 9\\n\"], \"outputs\": [\"4\", \"3\", \"-1\", \"-1\", \"4\", \"5\", \"30\", \"35\", \"3\", \"3\", \"3\", \"3\", \"7\", \"15\", \"10\", \"20\", \"15\", \"17\", \"6\", \"10\", \"11\", \"17\", \"-1\", \"3\", \"3\", \"3\", \"3\", \"3\", \"3\", \"3\", \"3\", \"6\", \"7\", \"8\", \"9\", \"10\", \"12\", \"14\", \"18\", \"25\", \"-1\", \"4\", \"3\", \"3\", \"-1\", \"5\", \"15\", \"10\", \"30\", \"17\", \"5\", \"10\", \"3\", \"4\", \"4\", \"3\", \"3\", \"3\", \"4\", \"3\", \"4\", \"4\", \"3\", \"3\", \"-1\", \"12\", \"5\", \"10\", \"4\", \"3\", \"3\", \"10\", \"17\", \"35\", \"11\", \"3\", \"-1\", \"4\", \"6\", \"3\", \"30\", \"3\", \"3\", \"5\", \"10\", \"3\", \"15\", \"8\", \"17\", \"15\", \"5\", \"20\", \"14\", \"10\", \"3\", \"3\", \"25\", \"3\", \"30\", \"6\", \"3\", \"-1\", \"3\", \"4\", \"4\", \"7\", \"17\", \"15\", \"4\", \"4\", \"3\", \"3\", \"3\", \"18\", \"3\", \"3\", \"3\", \"3\", \"10\", \"9\", \"4\", \"-1\", \"3\", \"7\", \"3\", \"3\\n\", \"-1\\n\", \"17\\n\", \"15\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"-1\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"-1\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"-1\\n\", \"3\\n\", \"-1\\n\", \"3\\n\", \"-1\\n\", \"-1\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"-1\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"17\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"3\\n\", \"-1\", \"3\", \"4\"]}", "source": "taco"}
|
You are given $n$ integer numbers $a_1, a_2, \dots, a_n$. Consider graph on $n$ nodes, in which nodes $i$, $j$ ($i\neq j$) are connected if and only if, $a_i$ AND $a_j\neq 0$, where AND denotes the bitwise AND operation.
Find the length of the shortest cycle in this graph or determine that it doesn't have cycles at all.
-----Input-----
The first line contains one integer $n$ $(1 \le n \le 10^5)$ — number of numbers.
The second line contains $n$ integer numbers $a_1, a_2, \dots, a_n$ ($0 \le a_i \le 10^{18}$).
-----Output-----
If the graph doesn't have any cycles, output $-1$. Else output the length of the shortest cycle.
-----Examples-----
Input
4
3 6 28 9
Output
4
Input
5
5 12 9 16 48
Output
3
Input
4
1 2 4 8
Output
-1
-----Note-----
In the first example, the shortest cycle is $(9, 3, 6, 28)$.
In the second example, the shortest cycle is $(5, 12, 9)$.
The graph has no cycles in the third example.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.25
|
{"tests": "{\"inputs\": [\"6 7\\n1 2\\n1 3\\n2 4\\n3 4\\n3 5\\n4 6\\n5 6\\n\", \"5 6\\n1 2\\n1 4\\n2 3\\n3 4\\n2 5\\n3 5\\n\", \"1 0\\n\", \"8 9\\n1 2\\n1 3\\n2 4\\n2 7\\n3 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"4 4\\n1 2\\n1 3\\n3 4\\n1 4\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 4\\n3 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 6\\n3 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 6\\n3 5\\n4 1\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n4 6\\n4 8\\n2 3\\n3 4\\n\", \"4 4\\n1 2\\n1 3\\n2 4\\n1 4\\n\", \"4 4\\n1 2\\n2 3\\n2 4\\n1 4\\n\", \"5 6\\n1 2\\n1 4\\n1 3\\n3 4\\n2 5\\n3 5\\n\", \"4 4\\n1 2\\n2 3\\n3 4\\n1 3\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 4\\n3 5\\n1 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 5\\n3 6\\n3 5\\n4 1\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 5\\n3 6\\n3 5\\n4 2\\n5 6\\n\", \"5 6\\n1 2\\n1 4\\n2 3\\n3 4\\n2 4\\n3 5\\n\", \"8 9\\n1 2\\n1 3\\n2 4\\n2 7\\n4 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n3 6\\n3 5\\n4 6\\n5 6\\n\", \"4 4\\n1 3\\n2 3\\n2 4\\n1 4\\n\", \"6 7\\n1 2\\n1 4\\n2 6\\n3 6\\n3 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n3 6\\n3 5\\n4 6\\n1 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n2 6\\n4 8\\n2 3\\n3 4\\n\", \"4 4\\n1 2\\n1 3\\n3 4\\n2 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n1 5\\n4 6\\n4 8\\n2 3\\n3 4\\n\", \"5 6\\n1 2\\n1 4\\n1 3\\n3 4\\n2 5\\n1 5\\n\", \"6 7\\n1 2\\n1 3\\n2 5\\n3 6\\n4 5\\n4 1\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n2 4\\n4 7\\n4 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n1 6\\n3 6\\n3 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 4\\n2 6\\n1 6\\n3 5\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n2 5\\n4 7\\n4 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n2 4\\n1 4\\n3 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 4\\n3 5\\n4 6\\n2 6\\n\", \"6 7\\n1 3\\n1 4\\n2 6\\n1 6\\n3 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n3 4\\n3 5\\n4 6\\n5 6\\n\", \"4 4\\n1 4\\n1 3\\n3 4\\n2 4\\n\", \"6 7\\n1 2\\n1 3\\n2 4\\n3 4\\n1 5\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n4 6\\n3 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n3 6\\n1 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 6\\n2 6\\n3 6\\n3 2\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n2 8\\n4 7\\n4 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 4\\n2 6\\n3 4\\n3 5\\n1 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 4\\n3 4\\n3 5\\n1 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n2 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n1 6\\n3 4\\n3 5\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n2 6\\n4 7\\n4 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 4\\n2 3\\n3 4\\n4 5\\n1 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n4 6\\n6 8\\n2 3\\n2 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n3 5\\n4 6\\n6 8\\n2 3\\n2 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n3 6\\n4 8\\n2 4\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n3 7\\n3 5\\n4 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n4 5\\n3 6\\n3 5\\n4 1\\n5 6\\n\", \"6 7\\n1 2\\n1 6\\n2 4\\n3 4\\n1 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n1 6\\n1 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 4\\n2 6\\n3 2\\n3 5\\n1 6\\n5 6\\n\", \"8 9\\n1 2\\n1 5\\n2 6\\n4 7\\n4 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n2 5\\n4 6\\n6 8\\n2 3\\n2 4\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n1 6\\n1 5\\n4 3\\n5 6\\n\", \"6 7\\n1 2\\n1 4\\n2 6\\n3 2\\n3 5\\n1 6\\n5 1\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n1 6\\n1 5\\n4 3\\n5 3\\n\", \"5 6\\n1 2\\n1 4\\n2 3\\n3 4\\n2 5\\n4 5\\n\", \"4 4\\n1 2\\n1 3\\n2 3\\n1 4\\n\", \"5 6\\n1 2\\n2 4\\n1 3\\n3 4\\n2 5\\n1 5\\n\", \"6 7\\n1 2\\n1 3\\n1 6\\n3 6\\n3 2\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n1 4\\n3 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n2 4\\n2 6\\n3 4\\n3 5\\n1 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n2 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n2 4\\n2 7\\n3 5\\n4 6\\n6 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n2 6\\n4 7\\n4 5\\n5 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n3 7\\n3 5\\n4 6\\n4 8\\n2 4\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 4\\n4 1\\n1 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 6\\n3 5\\n4 5\\n5 6\\n\", \"5 6\\n1 2\\n2 4\\n1 4\\n3 4\\n2 5\\n1 5\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n2 5\\n4 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n2 6\\n4 7\\n4 5\\n5 3\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n3 5\\n4 6\\n4 8\\n2 4\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n4 5\\n4 6\\n4 8\\n2 4\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n4 5\\n7 6\\n4 8\\n2 4\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n4 6\\n4 8\\n2 3\\n3 7\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n3 6\\n3 5\\n4 1\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 4\\n3 5\\n3 6\\n2 6\\n\", \"6 7\\n1 3\\n1 4\\n2 6\\n1 6\\n3 5\\n4 5\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n3 4\\n1 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 5\\n2 3\\n3 4\\n3 5\\n1 6\\n5 6\\n\", \"8 9\\n1 2\\n1 5\\n2 6\\n4 7\\n3 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 5\\n2 6\\n1 7\\n3 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n2 3\\n2 5\\n3 6\\n3 5\\n4 2\\n5 6\\n\", \"6 7\\n1 2\\n1 6\\n2 4\\n3 6\\n3 5\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n1 5\\n4 6\\n1 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n2 5\\n3 6\\n4 5\\n4 1\\n2 6\\n\", \"6 7\\n1 2\\n1 3\\n2 4\\n1 4\\n3 2\\n4 6\\n5 6\\n\", \"6 7\\n1 3\\n1 4\\n2 6\\n1 6\\n3 5\\n3 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 4\\n1 4\\n1 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 6\\n2 6\\n3 4\\n3 2\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n3 5\\n4 6\\n6 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n4 5\\n3 6\\n4 8\\n2 4\\n3 4\\n\", \"6 7\\n1 2\\n1 6\\n2 4\\n3 6\\n1 5\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n2 5\\n3 6\\n4 8\\n2 3\\n3 8\\n\", \"6 7\\n1 2\\n1 6\\n2 3\\n3 6\\n3 5\\n4 5\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n3 4\\n1 5\\n4 1\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n3 5\\n4 6\\n3 8\\n2 4\\n3 2\\n\", \"6 7\\n1 3\\n1 4\\n2 6\\n1 5\\n3 5\\n3 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 4\\n1 4\\n2 5\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n2 5\\n3 6\\n1 8\\n2 3\\n3 8\\n\", \"6 7\\n1 5\\n2 3\\n2 5\\n3 6\\n3 5\\n4 2\\n5 6\\n\", \"6 7\\n1 3\\n1 4\\n2 6\\n1 5\\n3 5\\n3 4\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n2 5\\n3 6\\n1 8\\n4 3\\n3 8\\n\", \"6 7\\n1 3\\n1 4\\n2 6\\n1 5\\n2 5\\n3 4\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 6\\n3 5\\n4 2\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 5\\n3 6\\n3 4\\n4 1\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n3 7\\n1 5\\n4 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n2 5\\n1 6\\n4 5\\n4 1\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n4 5\\n4 6\\n3 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n2 6\\n3 2\\n1 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 4\\n3 6\\n3 2\\n3 5\\n1 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n1 5\\n8 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n4 5\\n4 6\\n7 8\\n2 4\\n3 4\\n\", \"6 7\\n1 3\\n2 4\\n2 6\\n1 6\\n3 5\\n4 5\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n2 6\\n4 7\\n4 5\\n3 6\\n5 8\\n2 3\\n6 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n6 5\\n4 6\\n6 8\\n2 3\\n2 4\\n\", \"6 7\\n1 4\\n2 3\\n2 5\\n3 6\\n3 5\\n4 3\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n2 4\\n3 5\\n4 6\\n5 4\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 6\\n1 5\\n4 2\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 5\\n3 6\\n6 4\\n4 1\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 5\\n1 6\\n4 5\\n5 1\\n5 6\\n\", \"6 7\\n1 2\\n2 4\\n3 6\\n3 2\\n3 5\\n1 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n1 5\\n4 6\\n6 8\\n2 3\\n2 4\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 6\\n1 5\\n4 2\\n5 4\\n\", \"6 7\\n1 2\\n2 3\\n2 5\\n3 6\\n6 4\\n4 1\\n5 6\\n\", \"6 7\\n1 2\\n2 3\\n2 4\\n3 4\\n3 5\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n5 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n2 4\\n2 7\\n3 5\\n3 6\\n4 8\\n2 3\\n6 4\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 6\\n1 5\\n4 1\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n2 4\\n4 7\\n4 5\\n3 6\\n4 8\\n2 5\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n2 4\\n1 4\\n3 5\\n4 5\\n5 6\\n\", \"6 7\\n1 2\\n2 3\\n2 6\\n1 6\\n1 5\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n4 6\\n7 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 4\\n2 6\\n5 2\\n3 5\\n1 6\\n5 1\\n\", \"6 7\\n1 2\\n1 3\\n1 6\\n3 6\\n4 3\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n2 4\\n3 5\\n4 6\\n5 6\\n\", \"8 9\\n1 2\\n1 5\\n1 4\\n1 7\\n2 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n2 6\\n4 7\\n4 5\\n5 8\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n2 4\\n1 7\\n2 5\\n4 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n4 5\\n4 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 5\\n2 6\\n6 7\\n3 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n3 5\\n4 6\\n4 8\\n2 7\\n3 2\\n\", \"8 9\\n1 2\\n1 5\\n2 6\\n1 7\\n3 7\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n2 3\\n2 5\\n4 6\\n3 5\\n4 2\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 4\\n1 4\\n1 6\\n4 6\\n5 6\\n\", \"6 7\\n1 3\\n1 4\\n3 6\\n1 5\\n2 5\\n3 4\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 4\\n3 5\\n4 6\\n2 4\\n\", \"4 4\\n1 2\\n2 3\\n4 3\\n1 4\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 6\\n1 5\\n4 1\\n1 6\\n\", \"6 7\\n1 3\\n1 4\\n2 6\\n1 6\\n3 5\\n4 3\\n5 6\\n\", \"8 9\\n1 2\\n1 5\\n1 4\\n1 7\\n2 5\\n3 6\\n4 8\\n2 3\\n3 8\\n\", \"8 9\\n1 2\\n1 3\\n1 6\\n4 7\\n4 5\\n5 8\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 6\\n2 6\\n3 6\\n3 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 4\\n2 3\\n3 4\\n3 5\\n1 6\\n5 6\\n\", \"4 4\\n1 2\\n2 3\\n3 4\\n2 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n4 6\\n6 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 3\\n2 4\\n3 6\\n3 5\\n4 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 4\\n4 5\\n1 6\\n5 6\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 6\\n3 5\\n4 3\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n1 5\\n8 6\\n4 8\\n2 3\\n3 4\\n\", \"6 7\\n1 2\\n1 4\\n2 3\\n3 4\\n3 5\\n1 3\\n5 6\\n\", \"4 4\\n1 3\\n2 3\\n3 4\\n1 4\\n\", \"4 4\\n1 2\\n1 3\\n1 4\\n2 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n1 7\\n3 5\\n4 6\\n4 8\\n2 4\\n3 2\\n\", \"4 4\\n1 2\\n2 3\\n3 1\\n1 4\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n4 6\\n3 5\\n4 1\\n5 6\\n\", \"5 6\\n1 2\\n1 5\\n2 3\\n3 4\\n2 4\\n3 5\\n\", \"6 7\\n1 2\\n1 4\\n2 5\\n3 4\\n3 5\\n1 6\\n5 6\\n\", \"4 4\\n1 3\\n2 3\\n3 4\\n2 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n1 5\\n4 6\\n6 8\\n2 3\\n3 4\\n\", \"8 9\\n1 2\\n1 3\\n2 6\\n4 7\\n4 5\\n3 6\\n5 8\\n2 3\\n3 4\\n\", \"6 7\\n1 4\\n2 3\\n2 5\\n3 6\\n3 5\\n4 2\\n5 6\\n\", \"4 4\\n1 4\\n2 3\\n3 4\\n2 4\\n\", \"6 7\\n1 2\\n1 3\\n2 3\\n3 4\\n3 5\\n4 6\\n5 4\\n\", \"6 7\\n1 3\\n1 4\\n2 6\\n3 2\\n3 5\\n1 6\\n5 1\\n\", \"4 4\\n1 2\\n1 3\\n4 3\\n1 4\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n3 7\\n1 5\\n4 6\\n6 8\\n2 3\\n3 4\\n\", \"6 7\\n1 3\\n2 4\\n2 6\\n1 6\\n3 5\\n4 5\\n5 1\\n\", \"6 7\\n1 2\\n1 4\\n2 6\\n1 6\\n3 5\\n4 3\\n5 6\\n\", \"8 9\\n1 2\\n1 3\\n2 4\\n2 7\\n3 5\\n4 6\\n6 8\\n2 3\\n1 4\\n\", \"4 4\\n1 2\\n2 3\\n1 4\\n2 4\\n\", \"6 7\\n1 4\\n2 4\\n3 6\\n3 2\\n3 5\\n1 6\\n5 6\\n\", \"6 7\\n1 3\\n2 4\\n2 6\\n1 6\\n3 5\\n4 3\\n5 1\\n\", \"8 9\\n1 2\\n1 3\\n1 4\\n2 7\\n3 5\\n3 6\\n4 8\\n2 3\\n3 4\\n\", \"4 4\\n1 2\\n2 3\\n3 4\\n1 4\\n\"], \"outputs\": [\"4 1 2 0 1 0\\n1 4 0 2 0 1\\n2 0 4 1 2 0\\n0 2 1 4 0 2\\n1 0 2 0 4 1\\n0 1 0 2 1 4\\n\", \"2 1 0 0 0\\n1 2 0 0 0\\n0 0 2 1 0\\n0 0 1 2 0\\n0 0 0 0 1\\n\", \"1\\n\", \"2 0 0 0 0 0 0 0\\n0 1 0 0 0 0 1 0\\n0 0 1 0 1 1 0 0\\n0 0 0 2 0 0 0 2\\n0 0 1 0 1 1 0 0\\n0 0 1 0 1 1 0 0\\n0 1 0 0 0 0 1 0\\n0 0 0 2 0 0 0 2\\n\", \"1 1 0 0\\n1 1 0 0\\n0 0 1 0\\n0 0 0 1\\n\", \"2 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 2 1 1 0\\n0 0 1 2 0 1\\n0 0 1 0 2 1\\n0 0 0 1 1 2\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 1\\n0 0 0 0 1 0\\n0 0 0 1 0 1\\n\", \"1 0 0 1 0 0\\n0 1 0 0 0 0\\n0 0 1 0 0 0\\n1 0 0 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 2 0 0 0 0 2 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 1 0\\n0 1 0 0\\n1 0 1 0\\n0 0 0 1\\n\", \"1 0 0 0\\n0 1 1 0\\n0 1 1 0\\n0 0 0 1\\n\", \"2 1 0 0 0\\n1 2 0 0 0\\n0 0 2 0 1\\n0 0 0 1 0\\n0 0 1 0 2\\n\", \"1 0 0 0\\n0 1 0 0\\n0 0 1 1\\n0 0 1 1\\n\", \"2 0 0 0 0 1\\n0 1 0 0 0 0\\n0 0 2 2 1 0\\n0 0 2 2 1 0\\n0 0 1 1 2 0\\n1 0 0 0 0 2\\n\", \"2 0 1 2 0 0\\n0 2 0 0 1 0\\n1 0 2 1 0 0\\n2 0 1 2 0 0\\n0 1 0 0 2 0\\n0 0 0 0 0 1\\n\", \"2 0 1 0 0 0\\n0 2 0 2 1 0\\n1 0 2 0 0 0\\n0 2 0 2 1 0\\n0 1 0 1 2 0\\n0 0 0 0 0 1\\n\", \"2 0 0 0 0\\n0 1 0 0 0\\n0 0 2 0 2\\n0 0 0 1 0\\n0 0 2 0 2\\n\", \"2 0 0 0 0 0 0 0\\n0 1 0 0 0 0 1 0\\n0 0 1 0 0 1 0 0\\n0 0 0 2 2 0 0 2\\n0 0 0 2 2 0 0 2\\n0 0 1 0 0 1 0 0\\n0 1 0 0 0 0 1 0\\n0 0 0 2 2 0 0 2\\n\", \"2 0 1 0 0 0\\n0 2 0 1 0 1\\n1 0 2 0 0 0\\n0 1 0 2 0 2\\n0 0 0 0 1 0\\n0 1 0 2 0 2\\n\", \"2 0 1 1\\n0 2 1 1\\n1 1 2 0\\n1 1 0 2\\n\", \"2 1 0 1 0 0\\n1 2 0 0 0 1\\n0 0 2 0 0 0\\n1 0 0 2 0 1\\n0 0 0 0 2 0\\n0 1 0 1 0 2\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 2 0 2 0\\n0 0 0 1 0 1\\n0 0 2 0 2 0\\n0 0 0 1 0 1\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 2 2 0\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 0 0 2\\n0 0 1 0 1 0 0 0\\n0 2 0 0 0 2 2 0\\n0 2 0 0 0 2 2 0\\n0 0 0 2 0 0 0 2\\n\", \"2 1 1 0\\n1 2 0 1\\n1 0 2 1\\n0 1 1 2\\n\", \"1 0 0 0 1 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 0 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 2 0 0 0 0 2 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0\\n0 1 0 0 0\\n0 0 1 0 0\\n0 0 0 1 0\\n0 0 0 0 1\\n\", \"2 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 2 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 1\\n\", \"2 0 0 0 0 0 0 0\\n0 1 0 0 0 0 0 0\\n0 0 1 0 0 1 0 0\\n0 0 0 2 2 0 2 2\\n0 0 0 2 2 0 2 2\\n0 0 1 0 0 1 0 0\\n0 0 0 2 2 0 2 2\\n0 0 0 2 2 0 2 2\\n\", \"2 2 0 0 0 0\\n2 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 1\\n0 0 0 0 2 0\\n0 0 0 1 0 1\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 1 1\\n0 0 0 2 0 0\\n0 0 1 0 1 1\\n0 0 1 0 1 1\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 1 0 0 0\\n0 0 2 1 0 2 1 1\\n0 0 1 2 0 1 2 2\\n0 1 0 0 2 0 0 0\\n0 0 2 1 0 2 1 1\\n0 0 1 2 0 1 2 2\\n0 0 1 2 0 1 2 2\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 1\\n0 0 2 1 2 0\\n0 0 1 2 1 0\\n0 0 2 1 2 0\\n0 1 0 0 0 2\\n\", \"2 0 1 0 0 0\\n0 2 0 0 1 2\\n1 0 2 0 0 0\\n0 0 0 1 0 0\\n0 1 0 0 2 1\\n0 2 0 0 1 2\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 2 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 2\\n\", \"1 0 0 0\\n0 1 0 1\\n0 0 1 0\\n0 1 0 1\\n\", \"2 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 2 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 1 0 0 1\\n0 0 0 2 0 2 0 0\\n0 0 1 0 1 0 0 1\\n0 0 0 2 0 2 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 1 0 0 1\\n\", \"3 1 1 0 1 0\\n1 4 0 1 0 1\\n1 0 4 1 0 1\\n0 1 1 3 1 3\\n1 0 0 1 4 1\\n0 1 1 3 1 3\\n\", \"2 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 1 1 1\\n0 0 0 1 1 1\\n0 0 0 1 1 1\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 0 1\\n0 0 2 1 1 2 1 0\\n0 0 1 2 2 1 2 0\\n0 0 1 2 2 1 2 0\\n0 0 2 1 1 2 1 0\\n0 0 1 2 2 1 2 0\\n0 1 0 0 0 0 0 2\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"4 2 1 0 0 2\\n2 4 0 1 0 1\\n1 0 4 2 2 0\\n0 1 2 4 1 0\\n0 0 2 1 4 1\\n2 1 0 0 1 4\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 2 0 2 0\\n0 0 1 0 0 1 0 0\\n0 0 0 2 0 0 0 2\\n0 2 0 0 2 0 2 0\\n0 0 1 0 0 1 0 0\\n0 2 0 0 2 0 2 0\\n0 0 0 2 0 0 0 2\\n\", \"4 4 1 0 0 1\\n4 4 1 0 0 1\\n1 1 3 1 1 0\\n0 0 1 4 0 1\\n0 0 1 0 4 1\\n1 1 0 1 1 3\\n\", \"2 0 0 0 0 0 0 0\\n0 1 0 0 0 0 0 0\\n0 0 1 1 1 0 1 1\\n0 0 1 1 1 0 1 1\\n0 0 1 1 1 0 1 1\\n0 0 0 0 0 2 0 0\\n0 0 1 1 1 0 1 1\\n0 0 1 1 1 0 1 1\\n\", \"4 2 0 1 0 2\\n2 4 1 0 0 1\\n0 1 4 2 1 0\\n1 0 2 4 2 0\\n0 0 1 2 4 1\\n2 1 0 0 1 4\\n\", \"1 0 0 0 0 0 0 0\\n0 1 0 0 0 0 1 0\\n0 0 2 0 2 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 2 0 2 0 0 0\\n0 0 0 2 0 2 0 2\\n0 1 0 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0 0 1 0\\n0 1 0 0 0 0 0 0\\n0 0 2 0 2 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 2 0 2 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 2 0 2 2 0 0\\n0 0 0 1 0 0 0 1\\n0 0 2 0 2 2 0 0\\n0 0 2 0 2 2 0 0\\n0 2 0 0 0 0 2 0\\n0 0 0 1 0 0 0 1\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 0 0\\n0 0 1 0 1 0 1 0\\n0 0 0 2 0 2 0 2\\n0 0 1 0 1 0 1 0\\n0 0 0 2 0 2 0 2\\n0 0 1 0 1 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"2 2 1 0 0 0\\n2 2 1 0 0 0\\n1 1 2 0 0 0\\n0 0 0 2 1 0\\n0 0 0 1 2 0\\n0 0 0 0 0 1\\n\", \"2 1 0 0 0 0\\n1 2 0 0 0 0\\n0 0 2 2 0 1\\n0 0 2 2 0 1\\n0 0 0 0 1 0\\n0 0 1 1 0 2\\n\", \"1 0 1 0 0 0\\n0 2 0 0 0 0\\n1 0 1 0 0 0\\n0 0 0 1 0 1\\n0 0 0 0 2 0\\n0 0 0 1 0 1\\n\", \"1 0 0 1 0 0\\n0 2 1 0 0 0\\n0 1 2 0 0 0\\n1 0 0 1 0 0\\n0 0 0 0 2 1\\n0 0 0 0 1 2\\n\", \"1 0 0 0 0 0 0 0\\n0 1 0 0 0 0 0 0\\n0 0 1 0 0 0 0 0\\n0 0 0 1 0 0 1 1\\n0 0 0 0 2 0 0 0\\n0 0 0 0 0 2 0 0\\n0 0 0 1 0 0 1 1\\n0 0 0 1 0 0 1 1\\n\", \"1 0 0 0 0 0 1 0\\n0 1 0 0 1 0 0 0\\n0 0 2 0 0 0 0 0\\n0 0 0 2 0 2 0 2\\n0 1 0 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 1 1 0 0\\n0 2 0 0 0 0\\n1 0 1 1 0 0\\n1 0 1 1 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 1\\n\", \"2 0 0 2 1 0\\n0 2 1 0 0 0\\n0 1 2 0 0 0\\n2 0 0 2 1 0\\n1 0 0 1 2 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 1 0 0\\n0 0 1 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"4 1 0 1 0\\n1 3 1 0 1\\n0 1 4 1 0\\n1 0 1 3 1\\n0 1 0 1 4\\n\", \"1 0 0 1\\n0 1 0 0\\n0 0 1 0\\n1 0 0 1\\n\", \"2 0 1 0 0\\n0 2 0 1 0\\n1 0 2 0 0\\n0 1 0 2 0\\n0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 2 2 2\\n0 0 0 2 2 2\\n0 0 0 2 2 2\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 2\\n\", \"2 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0 1 0\\n0 2 0 0 2 0 0 0\\n0 0 1 0 0 1 0 0\\n0 0 0 2 0 0 0 2\\n0 2 0 0 2 0 0 0\\n0 0 1 0 0 1 0 0\\n1 0 0 0 0 0 1 0\\n0 0 0 2 0 0 0 2\\n\", \"2 0 0 0 0 0 0 0\\n0 1 0 0 0 0 1 0\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 1 0 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"2 0 0 0 0 0 0 0\\n0 1 0 0 0 0 0 0\\n0 0 1 0 0 0 0 0\\n0 0 0 1 0 0 1 1\\n0 0 0 0 2 0 0 0\\n0 0 0 0 0 1 0 0\\n0 0 0 1 0 0 1 1\\n0 0 0 1 0 0 1 1\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 0 0\\n0 0 2 0 2 0 2 0\\n0 0 0 1 0 1 0 1\\n0 0 2 0 2 0 2 0\\n0 0 0 1 0 1 0 1\\n0 0 2 0 2 0 2 0\\n0 0 0 1 0 1 0 1\\n\", \"1 0 0 0 1 1\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 2 0 0\\n1 0 0 0 1 1\\n1 0 0 0 1 1\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 1 0\\n0 0 0 1 1 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0\\n0 1 0 0 0\\n0 0 2 2 0\\n0 0 2 2 0\\n0 0 0 0 2\\n\", \"1 0 0 0 0 0 1 0\\n0 2 0 0 2 0 0 0\\n0 0 1 0 0 0 0 0\\n0 0 0 2 0 2 0 2\\n0 2 0 0 2 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0 0 0 0\\n0 1 0 0 0 1 0 0\\n0 0 1 0 0 0 0 0\\n0 0 0 1 0 0 1 1\\n0 0 0 0 1 0 0 0\\n0 1 0 0 0 1 0 0\\n0 0 0 1 0 0 1 1\\n0 0 0 1 0 0 1 1\\n\", \"1 0 0 0 0 0 1 0\\n0 2 0 0 0 0 0 0\\n0 0 2 0 2 0 0 0\\n0 0 0 1 0 1 0 1\\n0 0 2 0 2 0 0 0\\n0 0 0 1 0 1 0 1\\n1 0 0 0 0 0 1 0\\n0 0 0 1 0 1 0 1\\n\", \"1 0 0 0 0 0 1 0\\n0 2 0 0 0 0 0 0\\n0 0 2 0 0 0 0 0\\n0 0 0 1 1 1 0 1\\n0 0 0 1 1 1 0 1\\n0 0 0 1 1 1 0 1\\n1 0 0 0 0 0 1 0\\n0 0 0 1 1 1 0 1\\n\", \"1 0 0 0 0 1 1 0\\n0 2 0 0 0 0 0 0\\n0 0 2 0 0 0 0 0\\n0 0 0 1 1 0 0 1\\n0 0 0 1 1 0 0 1\\n1 0 0 0 0 1 1 0\\n1 0 0 0 0 1 1 0\\n0 0 0 1 1 0 0 1\\n\", \"2 0 0 2 0 2 0 2\\n0 1 0 0 0 0 0 0\\n0 0 1 0 1 0 0 0\\n2 0 0 2 0 2 0 2\\n0 0 1 0 1 0 0 0\\n2 0 0 2 0 2 0 2\\n0 0 0 0 0 0 2 0\\n2 0 0 2 0 2 0 2\\n\", \"2 0 1 2 0 0\\n0 2 0 0 0 1\\n1 0 2 1 0 0\\n2 0 1 2 0 0\\n0 0 0 0 1 0\\n0 1 0 0 0 2\\n\", \"2 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 1 1 0\\n0 0 1 1 1 0\\n0 0 1 1 1 0\\n0 0 0 0 0 2\\n\", \"3 1 1 1 0 1\\n1 4 0 0 1 4\\n1 0 4 0 1 0\\n1 0 0 4 1 0\\n0 1 1 1 3 1\\n1 4 0 0 1 4\\n\", \"2 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 2\\n\", \"2 1 0 0 0 0\\n1 2 0 0 0 0\\n0 0 2 2 1 0\\n0 0 2 2 1 0\\n0 0 1 1 2 0\\n0 0 0 0 0 1\\n\", \"2 1 0 0 0 0 0 0\\n1 2 0 0 0 0 0 0\\n0 0 2 2 1 0 2 2\\n0 0 2 2 1 0 2 2\\n0 0 1 1 2 0 1 1\\n0 0 0 0 0 1 0 0\\n0 0 2 2 1 0 2 2\\n0 0 2 2 1 0 2 2\\n\", \"2 1 0 0 0 0 2 0\\n1 2 0 0 0 0 1 0\\n0 0 2 2 1 0 0 2\\n0 0 2 2 1 0 0 2\\n0 0 1 1 2 0 0 1\\n0 0 0 0 0 1 0 0\\n2 1 0 0 0 0 2 0\\n0 0 2 2 1 0 0 2\\n\", \"2 2 0 2 0 0\\n2 2 0 2 0 0\\n0 0 1 0 0 0\\n2 2 0 2 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 2\\n\", \"2 1 0 0 0 1\\n1 2 0 1 0 0\\n0 0 2 0 0 0\\n0 1 0 2 0 1\\n0 0 0 0 2 0\\n1 0 0 1 0 2\\n\", \"1 0 0 0 1 0 0 1\\n0 2 0 0 0 0 2 0\\n0 0 1 0 0 0 0 0\\n0 0 0 2 0 2 0 0\\n1 0 0 0 1 0 0 1\\n0 0 0 2 0 2 0 0\\n0 2 0 0 0 0 2 0\\n1 0 0 0 1 0 0 1\\n\", \"4 1 2 2 0 0\\n1 4 0 0 2 2\\n2 0 4 1 0 1\\n2 0 1 4 1 0\\n0 2 0 1 4 1\\n0 2 1 0 1 4\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 2 2 2\\n0 0 0 2 2 2\\n0 0 0 2 2 2\\n\", \"2 0 0 2 0 0\\n0 1 0 0 0 1\\n0 0 1 0 0 0\\n2 0 0 2 0 0\\n0 0 0 0 2 0\\n0 1 0 0 0 1\\n\", \"2 0 2 0 1 0\\n0 1 0 0 0 0\\n2 0 2 0 1 0\\n0 0 0 2 0 1\\n1 0 1 0 2 0\\n0 0 0 1 0 2\\n\", \"1 0 0 0 0 0\\n0 2 1 0 0 0\\n0 1 2 0 0 0\\n0 0 0 2 1 1\\n0 0 0 1 2 2\\n0 0 0 1 2 2\\n\", \"1 0 0 0 0 0 1 0\\n0 2 0 0 0 0 0 0\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 2 0 0 2 0 0\\n0 0 0 1 1 0 0 1\\n0 0 0 1 1 0 0 1\\n0 0 2 0 0 2 0 0\\n0 2 0 0 0 0 2 0\\n0 0 0 1 1 0 0 1\\n\", \"2 1 0 0 0 0\\n1 2 0 0 0 0\\n0 0 2 1 0 2\\n0 0 1 2 0 1\\n0 0 0 0 1 0\\n0 0 2 1 0 2\\n\", \"2 0 0 1 0 0 2 0\\n0 1 0 0 1 0 0 0\\n0 0 2 0 0 2 0 1\\n1 0 0 2 0 0 1 0\\n0 1 0 0 1 0 0 0\\n0 0 2 0 0 2 0 1\\n2 0 0 1 0 0 2 0\\n0 0 1 0 0 1 0 2\\n\", \"2 0 0 0 0 1\\n0 2 1 0 0 0\\n0 1 2 0 0 0\\n0 0 0 1 1 0\\n0 0 0 1 1 0\\n1 0 0 0 0 2\\n\", \"2 1 0 0 1 0\\n1 2 0 0 0 1\\n0 0 2 0 0 0\\n0 0 0 2 0 0\\n1 0 0 0 2 1\\n0 1 0 0 1 2\\n\", \"1 0 0 0 0 0 1 0\\n0 1 0 0 0 0 0 0\\n0 0 2 0 2 0 0 2\\n0 0 0 2 0 2 0 0\\n0 0 2 0 2 0 0 2\\n0 0 0 2 0 2 0 0\\n1 0 0 0 0 0 1 0\\n0 0 2 0 2 0 0 2\\n\", \"2 0 0 2 0 0\\n0 2 0 0 0 2\\n0 0 1 0 0 0\\n2 0 0 2 0 0\\n0 0 0 0 1 0\\n0 2 0 0 0 2\\n\", \"1 0 1 0 0 0\\n0 2 0 0 1 0\\n1 0 1 0 0 0\\n0 0 0 2 0 1\\n0 1 0 0 2 0\\n0 0 0 1 0 2\\n\", \"1 0 0 1 0 0 1 0\\n0 2 0 0 2 0 0 0\\n0 0 1 0 0 1 0 0\\n1 0 0 1 0 0 1 0\\n0 2 0 0 2 0 0 0\\n0 0 1 0 0 1 0 0\\n1 0 0 1 0 0 1 0\\n0 0 0 0 0 0 0 2\\n\", \"1 0 0 0 1 0\\n0 2 0 2 0 0\\n0 0 1 0 0 0\\n0 2 0 2 0 0\\n1 0 0 0 1 0\\n0 0 0 0 0 2\\n\", \"1 0 0 0 0 0\\n0 2 0 0 2 2\\n0 0 1 0 0 0\\n0 0 0 2 0 0\\n0 2 0 0 2 2\\n0 2 0 0 2 2\\n\", \"1 1 0 0 1 0 1 0\\n1 1 0 0 1 0 1 0\\n0 0 1 0 0 1 0 0\\n0 0 0 2 0 0 0 0\\n1 1 0 0 1 0 1 0\\n0 0 1 0 0 1 0 0\\n1 1 0 0 1 0 1 0\\n0 0 0 0 0 0 0 2\\n\", \"1 0 0 0 1 0\\n0 1 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n1 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 1 0 1 0 0\\n0 0 1 0 0 0\\n0 1 0 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 2 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 1 0 0 0\\n0 2 0 0 0 0 0 0\\n0 0 1 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 1 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"3 1 3 1 0 1\\n1 4 1 0 1 0\\n3 1 3 1 0 1\\n1 0 1 4 1 0\\n0 1 0 1 3 1\\n1 0 1 0 1 4\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 0 0 0 1\\n0 0 0 2 2 2 0 0\\n0 0 0 2 2 2 0 0\\n0 0 0 2 2 2 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 0 0 0 1\\n\", \"2 0 0 0 1 0\\n0 2 0 1 0 1\\n0 0 1 0 0 0\\n0 1 0 2 0 2\\n1 0 0 0 2 0\\n0 1 0 2 0 2\\n\", \"2 0 0 2 0 1\\n0 2 1 0 0 0\\n0 1 2 0 0 0\\n2 0 0 2 0 1\\n0 0 0 0 1 0\\n1 0 0 1 0 2\\n\", \"1 0 0 0 1 0 1 0\\n0 2 0 0 0 0 0 0\\n0 0 1 0 0 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 1 0 1 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 1 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0 0 1 1\\n0 2 0 0 0 0 0 0\\n0 0 2 0 0 0 0 0\\n0 0 0 1 1 1 0 0\\n0 0 0 1 1 1 0 0\\n0 0 0 1 1 1 0 0\\n1 0 0 0 0 0 1 1\\n1 0 0 0 0 0 1 1\\n\", \"4 1 1 0 0 2\\n1 4 0 1 0 2\\n1 0 4 1 2 0\\n0 1 1 4 2 0\\n0 0 2 2 4 1\\n2 2 0 0 1 4\\n\", \"2 0 0 0 0 0 0 0\\n0 1 0 0 0 0 0 0\\n0 0 1 0 0 0 0 0\\n0 0 0 2 2 2 2 2\\n0 0 0 2 2 2 2 2\\n0 0 0 2 2 2 2 2\\n0 0 0 2 2 2 2 2\\n0 0 0 2 2 2 2 2\\n\", \"1 0 0 0 0 0 1 0\\n0 1 0 0 0 0 0 0\\n0 0 2 0 0 0 0 0\\n0 0 0 2 2 2 0 2\\n0 0 0 2 2 2 0 2\\n0 0 0 2 2 2 0 2\\n1 0 0 0 0 0 1 0\\n0 0 0 2 2 2 0 2\\n\", \"1 0 1 1 0 0\\n0 2 0 0 0 0\\n1 0 1 1 0 0\\n1 0 1 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 2\\n\", \"1 0 0 0 0 0\\n0 2 0 1 0 1\\n0 0 2 0 1 0\\n0 1 0 2 0 2\\n0 0 1 0 2 0\\n0 1 0 2 0 2\\n\", \"2 0 0 0 1 0\\n0 1 0 1 0 0\\n0 0 2 0 0 1\\n0 1 0 1 0 0\\n1 0 0 0 2 0\\n0 0 1 0 0 2\\n\", \"2 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 2 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 2\\n\", \"1 0 1 0 0 0\\n0 2 0 0 0 0\\n1 0 1 0 0 0\\n0 0 0 1 1 0\\n0 0 0 1 1 0\\n0 0 0 0 0 2\\n\", \"2 0 0 0 0 1\\n0 2 1 2 0 0\\n0 1 2 1 0 0\\n0 2 1 2 0 0\\n0 0 0 0 1 0\\n1 0 0 0 0 2\\n\", \"1 0 0 0 1 0 1 0\\n0 1 0 0 0 0 0 0\\n0 0 2 0 0 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 1 0 1 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 1 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"2 0 0 0 1 0\\n0 2 0 1 0 0\\n0 0 1 0 0 1\\n0 1 0 2 0 0\\n1 0 0 0 2 0\\n0 0 1 0 0 1\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 2\\n\", \"1 1 0 0 0 0\\n1 1 0 0 0 0\\n0 0 2 0 1 0\\n0 0 0 2 0 1\\n0 0 1 0 2 0\\n0 0 0 1 0 2\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 1 1 0 0\\n0 0 0 2 0 0 0 2\\n0 0 1 0 1 1 0 0\\n0 0 1 0 1 1 0 0\\n0 2 0 0 0 0 2 0\\n0 0 0 2 0 0 0 2\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 1 0 0 2 1\\n0 0 2 0 2 1 0 0\\n0 1 0 2 0 0 1 2\\n0 0 2 0 2 1 0 0\\n0 0 1 0 1 2 0 0\\n0 2 0 1 0 0 2 1\\n0 1 0 2 0 0 1 2\\n\", \"2 0 0 2 1 0\\n0 1 0 0 0 0\\n0 0 2 0 0 1\\n2 0 0 2 1 0\\n1 0 0 1 2 0\\n0 0 1 0 0 2\\n\", \"2 1 0 0 0 0 0 0\\n1 2 0 0 0 0 0 0\\n0 0 2 1 0 2 1 1\\n0 0 1 2 0 1 2 2\\n0 0 0 0 1 0 0 0\\n0 0 2 1 0 2 1 1\\n0 0 1 2 0 1 2 2\\n0 0 1 2 0 1 2 2\\n\", \"2 0 1 0 0 0\\n0 1 0 0 0 0\\n1 0 2 0 0 0\\n0 0 0 2 1 1\\n0 0 0 1 2 2\\n0 0 0 1 2 2\\n\", \"1 0 0 0 0 0\\n0 2 2 0 0 0\\n0 2 2 0 0 0\\n0 0 0 1 0 1\\n0 0 0 0 2 0\\n0 0 0 1 0 1\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 2 2\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 0\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 0\\n0 2 0 0 0 0 2 2\\n0 2 0 0 0 0 2 2\\n\", \"1 0 0 1 0 0\\n0 1 0 0 0 0\\n0 0 2 0 2 0\\n1 0 0 1 0 0\\n0 0 2 0 2 0\\n0 0 0 0 0 2\\n\", \"2 2 0 0 0 0\\n2 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 2 0 0\\n0 0 0 0 1 1\\n0 0 0 0 1 1\\n\", \"2 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 2\\n\", \"2 0 0 1 0 0 2 1\\n0 2 1 0 0 1 0 0\\n0 1 2 0 0 2 0 0\\n1 0 0 2 0 0 1 2\\n0 0 0 0 1 0 0 0\\n0 1 2 0 0 2 0 0\\n2 0 0 1 0 0 2 1\\n1 0 0 2 0 0 1 2\\n\", \"1 0 0 0 0 0 0 0\\n0 1 0 0 0 1 0 0\\n0 0 1 1 0 0 1 0\\n0 0 1 1 0 0 1 0\\n0 0 0 0 1 0 0 0\\n0 1 0 0 0 1 0 0\\n0 0 1 1 0 0 1 0\\n0 0 0 0 0 0 0 1\\n\", \"2 0 0 0 0 0 2 0\\n0 1 0 0 1 0 0 0\\n0 0 1 0 0 0 0 0\\n0 0 0 2 0 2 0 2\\n0 1 0 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n2 0 0 0 0 0 2 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0 0 1 0\\n0 2 0 0 0 0 0 0\\n0 0 1 0 0 0 0 0\\n0 0 0 2 2 2 0 2\\n0 0 0 2 2 2 0 2\\n0 0 0 2 2 2 0 2\\n1 0 0 0 0 0 1 0\\n0 0 0 2 2 2 0 2\\n\", \"2 1 0 0 0 0 0 0\\n1 2 0 0 0 0 0 0\\n0 0 2 2 1 0 0 2\\n0 0 2 2 1 0 0 2\\n0 0 1 1 2 0 0 1\\n0 0 0 0 0 1 1 0\\n0 0 0 0 0 1 1 0\\n0 0 2 2 1 0 0 2\\n\", \"1 0 0 1 0 1 0 1\\n0 1 0 0 0 0 0 0\\n0 0 2 0 2 0 0 0\\n1 0 0 1 0 1 0 1\\n0 0 2 0 2 0 0 0\\n1 0 0 1 0 1 0 1\\n0 0 0 0 0 0 2 0\\n1 0 0 1 0 1 0 1\\n\", \"2 1 0 0 2 0 0 0\\n1 2 0 0 1 0 0 0\\n0 0 2 2 0 0 1 2\\n0 0 2 2 0 0 1 2\\n2 1 0 0 2 0 0 0\\n0 0 0 0 0 1 0 0\\n0 0 1 1 0 0 2 1\\n0 0 2 2 0 0 1 2\\n\", \"2 2 0 1 0 0\\n2 2 0 1 0 0\\n0 0 1 0 0 0\\n1 1 0 2 0 0\\n0 0 0 0 2 1\\n0 0 0 0 1 2\\n\", \"1 0 1 0 0 0\\n0 2 0 0 0 0\\n1 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 2 2\\n0 0 0 0 2 2\\n\", \"2 1 0 0 1 0\\n1 2 0 0 2 0\\n0 0 2 0 0 1\\n0 0 0 1 0 0\\n1 2 0 0 2 0\\n0 0 1 0 0 2\\n\", \"2 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 0 1 0\\n0 0 0 2 0 2\\n0 0 1 0 1 0\\n0 0 0 2 0 2\\n\", \"2 1 0 1\\n1 2 1 0\\n0 1 2 1\\n1 0 1 2\\n\", \"1 0 0 1 1 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n1 0 0 1 1 0\\n1 0 0 1 1 0\\n0 0 0 0 0 2\\n\", \"2 1 0 0 0 1\\n1 2 0 0 0 2\\n0 0 2 0 1 0\\n0 0 0 1 0 0\\n0 0 1 0 2 0\\n1 2 0 0 0 2\\n\", \"1 0 0 0 0 0 1 0\\n0 1 0 0 0 0 0 0\\n0 0 1 0 0 1 0 0\\n0 0 0 1 0 0 0 0\\n0 0 0 0 2 0 0 0\\n0 0 1 0 0 1 0 0\\n1 0 0 0 0 0 1 0\\n0 0 0 0 0 0 0 2\\n\", \"1 0 0 0 0 1 0 0\\n0 1 0 0 0 0 0 0\\n0 0 1 1 0 0 1 0\\n0 0 1 1 0 0 1 0\\n0 0 0 0 1 0 0 0\\n1 0 0 0 0 1 0 0\\n0 0 1 1 0 0 1 0\\n0 0 0 0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 1\\n0 0 0 0 1 0\\n0 0 0 1 0 1\\n\", \"2 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 2 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"1 1 0 0\\n1 1 0 0\\n0 0 1 0\\n0 0 0 1\\n\", \"1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 1 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 2 0 0 0 0 2 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 1 0 0\\n0 0 1 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 1 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 0 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 2 0 0 0 0 2 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 1 1\\n0 0 0 2 0 0\\n0 0 1 0 1 1\\n0 0 1 0 1 1\\n\", \"1 0 0 0\\n0 1 1 0\\n0 1 1 0\\n0 0 0 1\\n\", \"1 0 1 0\\n0 1 0 0\\n1 0 1 0\\n0 0 0 1\\n\", \"1 0 0 0 0 0 1 0\\n0 1 0 0 0 0 0 0\\n0 0 2 0 2 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 2 0 2 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 1\\n0 1 0 0\\n0 0 1 0\\n1 0 0 1\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 2\\n\", \"2 1 0 0 0\\n1 2 0 0 0\\n0 0 2 0 1\\n0 0 0 1 0\\n0 0 1 0 2\\n\", \"2 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 2\\n\", \"1 0 1 0\\n0 1 0 0\\n1 0 1 0\\n0 0 0 1\\n\", \"1 0 0 0 1 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 0 0 0 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 2 0 0 0 0 2 0\\n0 0 0 2 0 2 0 2\\n\", \"2 0 0 0 0 0 0 0\\n0 1 0 0 0 0 0 0\\n0 0 1 1 1 0 1 1\\n0 0 1 1 1 0 1 1\\n0 0 1 1 1 0 1 1\\n0 0 0 0 0 2 0 0\\n0 0 1 1 1 0 1 1\\n0 0 1 1 1 0 1 1\\n\", \"2 2 0 2 0 0\\n2 2 0 2 0 0\\n0 0 1 0 0 0\\n2 2 0 2 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 2\\n\", \"1 0 0 1\\n0 1 0 0\\n0 0 1 0\\n1 0 0 1\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 1\\n0 0 0 0 1 0\\n0 0 0 1 0 1\\n\", \"2 0 0 2 0 1\\n0 2 1 0 0 0\\n0 1 2 0 0 0\\n2 0 0 2 0 1\\n0 0 0 0 1 0\\n1 0 0 1 0 2\\n\", \"1 1 0 0\\n1 1 0 0\\n0 0 1 0\\n0 0 0 1\\n\", \"1 0 0 0 1 0 0 0\\n0 2 0 0 0 0 0 0\\n0 0 1 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n1 0 0 0 1 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 1 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 2 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 1 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0 0 0\\n0 1 0 0 0 0 1 0\\n0 0 2 0 2 0 0 0\\n0 0 0 2 0 2 0 2\\n0 0 2 0 2 0 0 0\\n0 0 0 2 0 2 0 2\\n0 1 0 0 0 0 1 0\\n0 0 0 2 0 2 0 2\\n\", \"1 0 0 0\\n0 1 1 0\\n0 1 1 0\\n0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 1 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 2 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 1\\n\", \"1 0 0 0 0 0\\n0 2 0 0 0 0\\n0 0 1 0 0 0\\n0 0 0 1 0 0\\n0 0 0 0 2 0\\n0 0 0 0 0 1\\n\", \"\\n1 0 0 0 0 0 0 0\\n0 2 0 0 0 0 2 0\\n0 0 1 0 1 1 0 0\\n0 0 0 2 0 0 0 2\\n0 0 1 0 1 1 0 0\\n0 0 1 0 1 1 0 0\\n0 2 0 0 0 0 2 0\\n0 0 0 2 0 0 0 2\\n\", \"\\n2 1 0 1\\n1 2 1 0\\n0 1 2 1\\n1 0 1 2\\n\"]}", "source": "taco"}
|
We define a spanning tree of a graph to be a BFS tree rooted at vertex s if and only if for every node t the shortest distance between s and t in the graph is equal to the shortest distance between s and t in the spanning tree.
Given a graph, we define f(x,y) to be the number of spanning trees of that graph that are BFS trees rooted at vertices x and y at the same time.
You are given an undirected connected graph with n vertices and m edges. Calculate f(i,j) for all i, j by modulo 998 244 353.
Input
The first line contains two integers n, m (1 ≤ n ≤ 400, 0 ≤ m ≤ 600) — the number of vertices and the number of edges in the graph.
The i-th of the next m lines contains two integers a_i, b_i (1 ≤ a_i, b_i ≤ n, a_i < b_i), representing an edge connecting a_i and b_i.
It is guaranteed that all edges are distinct and the graph is connected.
Output
Print n lines, each consisting of n integers.
The integer printed in the row i and the column j should be f(i,j) mod 998 244 353.
Examples
Input
4 4
1 2
2 3
3 4
1 4
Output
2 1 0 1
1 2 1 0
0 1 2 1
1 0 1 2
Input
8 9
1 2
1 3
1 4
2 7
3 5
3 6
4 8
2 3
3 4
Output
1 0 0 0 0 0 0 0
0 2 0 0 0 0 2 0
0 0 1 0 1 1 0 0
0 0 0 2 0 0 0 2
0 0 1 0 1 1 0 0
0 0 1 0 1 1 0 0
0 2 0 0 0 0 2 0
0 0 0 2 0 0 0 2
Note
The following picture describes the first example.
<image>
The tree with red edges is a BFS tree rooted at both 1 and 2.
<image>
Similarly, the BFS tree for other adjacent pairs of vertices can be generated in this way.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\\n2\\n3\\n5\\n\", \"9\\n15\\n7\\n12\\n122\\n127\\n99\\n1999999\\n255\\n8388607\\n\", \"1\\n228\\n\", \"1\\n228\\n\", \"9\\n15\\n7\\n12\\n122\\n127\\n99\\n1999999\\n255\\n8388607\\n\", \"1\\n88\\n\", \"9\\n15\\n7\\n12\\n122\\n127\\n99\\n1984716\\n255\\n8388607\\n\", \"1\\n11\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n99\\n1984716\\n255\\n8388607\\n\", \"1\\n19\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n99\\n1984716\\n204\\n8388607\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n71\\n1984716\\n204\\n14628115\\n\", \"1\\n4\\n\", \"9\\n30\\n7\\n4\\n122\\n127\\n92\\n1984716\\n168\\n14628115\\n\", \"1\\n7\\n\", \"9\\n30\\n7\\n4\\n122\\n226\\n92\\n1984716\\n168\\n14628115\\n\", \"9\\n30\\n7\\n4\\n122\\n226\\n170\\n1984716\\n168\\n14628115\\n\", \"1\\n245\\n\", \"9\\n15\\n7\\n12\\n122\\n127\\n99\\n533847\\n255\\n8388607\\n\", \"9\\n30\\n4\\n12\\n122\\n127\\n99\\n1984716\\n255\\n8388607\\n\", \"1\\n32\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n99\\n1984716\\n104\\n8388607\\n\", \"1\\n15\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n134\\n1984716\\n204\\n8388607\\n\", \"1\\n63\\n\", \"9\\n30\\n7\\n12\\n122\\n136\\n92\\n1984716\\n204\\n14628115\\n\", \"1\\n2\\n\", \"9\\n30\\n7\\n4\\n122\\n127\\n17\\n1984716\\n168\\n14628115\\n\", \"9\\n30\\n7\\n4\\n122\\n226\\n92\\n1984716\\n168\\n1710958\\n\", \"9\\n30\\n6\\n4\\n122\\n226\\n170\\n1984716\\n168\\n14628115\\n\", \"1\\n259\\n\", \"9\\n15\\n4\\n12\\n99\\n127\\n99\\n1999999\\n255\\n8388607\\n\", \"9\\n30\\n4\\n21\\n122\\n127\\n99\\n1984716\\n255\\n8388607\\n\", \"9\\n30\\n5\\n12\\n122\\n127\\n99\\n1984716\\n104\\n8388607\\n\", \"9\\n30\\n7\\n12\\n122\\n175\\n134\\n1984716\\n204\\n8388607\\n\", \"9\\n30\\n7\\n14\\n122\\n127\\n71\\n77725\\n204\\n14628115\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n92\\n1984716\\n168\\n17916425\\n\", \"9\\n30\\n7\\n4\\n226\\n127\\n17\\n1984716\\n168\\n14628115\\n\", \"9\\n30\\n6\\n4\\n122\\n226\\n170\\n1984716\\n100\\n14628115\\n\", \"9\\n15\\n4\\n12\\n99\\n127\\n58\\n1999999\\n255\\n8388607\\n\", \"9\\n30\\n4\\n21\\n122\\n210\\n99\\n1984716\\n255\\n8388607\\n\", \"9\\n30\\n5\\n12\\n122\\n127\\n99\\n1984716\\n104\\n660941\\n\", \"9\\n30\\n7\\n12\\n122\\n45\\n134\\n1984716\\n204\\n8388607\\n\", \"9\\n30\\n7\\n21\\n122\\n127\\n71\\n77725\\n204\\n14628115\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n92\\n1984716\\n168\\n1700009\\n\", \"9\\n30\\n7\\n4\\n122\\n327\\n92\\n1984716\\n177\\n1710958\\n\", \"9\\n15\\n4\\n7\\n99\\n127\\n58\\n1999999\\n255\\n8388607\\n\", \"9\\n15\\n7\\n12\\n79\\n127\\n55\\n805011\\n255\\n8388607\\n\", \"9\\n30\\n2\\n21\\n122\\n210\\n99\\n1984716\\n255\\n8388607\\n\", \"9\\n30\\n5\\n12\\n122\\n127\\n99\\n1984716\\n104\\n205715\\n\", \"9\\n30\\n7\\n12\\n122\\n6\\n134\\n1984716\\n204\\n8388607\\n\", \"9\\n30\\n7\\n12\\n122\\n171\\n92\\n1984716\\n168\\n1700009\\n\", \"9\\n30\\n6\\n4\\n122\\n226\\n383\\n1984716\\n100\\n14628115\\n\", \"9\\n28\\n5\\n4\\n95\\n226\\n170\\n1984716\\n227\\n7333744\\n\", \"9\\n30\\n2\\n33\\n122\\n210\\n99\\n1984716\\n255\\n8388607\\n\", \"9\\n30\\n4\\n14\\n122\\n127\\n71\\n77725\\n166\\n14628115\\n\", \"9\\n30\\n11\\n12\\n122\\n136\\n92\\n1984716\\n217\\n14628115\\n\", \"9\\n30\\n7\\n7\\n122\\n171\\n92\\n1984716\\n168\\n1700009\\n\", \"9\\n30\\n6\\n4\\n122\\n226\\n383\\n3214896\\n100\\n14628115\\n\", \"9\\n28\\n5\\n4\\n168\\n226\\n170\\n1984716\\n227\\n7333744\\n\", \"9\\n15\\n7\\n12\\n147\\n3\\n55\\n805011\\n255\\n8388607\\n\", \"9\\n30\\n2\\n33\\n122\\n281\\n99\\n1984716\\n255\\n8388607\\n\", \"1\\n9\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n71\\n1984716\\n204\\n8388607\\n\", \"1\\n17\\n\", \"1\\n10\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n92\\n1984716\\n204\\n14628115\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n92\\n1984716\\n168\\n14628115\\n\", \"1\\n8\\n\", \"1\\n6\\n\", \"1\\n13\\n\", \"9\\n30\\n7\\n4\\n95\\n226\\n170\\n1984716\\n168\\n14628115\\n\", \"9\\n15\\n7\\n12\\n99\\n127\\n99\\n1999999\\n255\\n8388607\\n\", \"1\\n97\\n\", \"1\\n3\\n\", \"9\\n30\\n7\\n14\\n122\\n127\\n71\\n1984716\\n204\\n14628115\\n\", \"9\\n30\\n7\\n12\\n122\\n127\\n92\\n1984716\\n168\\n12775309\\n\", \"1\\n12\\n\", \"1\\n5\\n\", \"1\\n20\\n\", \"9\\n30\\n7\\n4\\n95\\n226\\n170\\n1984716\\n227\\n14628115\\n\", \"1\\n33\\n\", \"9\\n15\\n7\\n12\\n79\\n127\\n99\\n533847\\n255\\n8388607\\n\", \"1\\n64\\n\", \"1\\n29\\n\", \"1\\n16\\n\", \"1\\n51\\n\", \"9\\n30\\n7\\n12\\n122\\n136\\n92\\n1984716\\n169\\n14628115\\n\", \"9\\n30\\n7\\n4\\n122\\n226\\n92\\n1984716\\n177\\n1710958\\n\", \"1\\n14\\n\", \"9\\n30\\n5\\n4\\n95\\n226\\n170\\n1984716\\n227\\n14628115\\n\", \"1\\n443\\n\", \"1\\n43\\n\", \"9\\n15\\n7\\n12\\n79\\n127\\n99\\n805011\\n255\\n8388607\\n\", \"1\\n60\\n\", \"1\\n24\\n\", \"1\\n71\\n\", \"9\\n30\\n7\\n12\\n122\\n136\\n92\\n1984716\\n224\\n14628115\\n\", \"9\\n30\\n6\\n4\\n122\\n226\\n228\\n1984716\\n100\\n14628115\\n\", \"1\\n22\\n\", \"9\\n28\\n5\\n4\\n95\\n226\\n170\\n1984716\\n227\\n14628115\\n\", \"1\\n273\\n\", \"1\\n58\\n\", \"1\\n89\\n\", \"1\\n37\\n\", \"3\\n2\\n3\\n5\\n\"], \"outputs\": [\"3\\n1\\n7\\n\", \"5\\n1\\n15\\n127\\n1\\n127\\n2097151\\n85\\n178481\\n\", \"255\\n\", \"255\\n\", \"5\\n1\\n15\\n127\\n1\\n127\\n2097151\\n85\\n178481\\n\", \"127\\n\", \"5\\n1\\n15\\n127\\n1\\n127\\n2097151\\n85\\n178481\\n\", \"15\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n85\\n178481\\n\", \"31\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n255\\n178481\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n255\\n16777215\\n\", \"7\\n\", \"31\\n1\\n7\\n127\\n1\\n127\\n2097151\\n255\\n16777215\\n\", \"1\\n\", \"31\\n1\\n7\\n127\\n255\\n127\\n2097151\\n255\\n16777215\\n\", \"31\\n1\\n7\\n127\\n255\\n255\\n2097151\\n255\\n16777215\\n\", \"255\\n\", \"5\\n1\\n15\\n127\\n1\\n127\\n1048575\\n85\\n178481\\n\", \"31\\n7\\n15\\n127\\n1\\n127\\n2097151\\n85\\n178481\\n\", \"63\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n127\\n178481\\n\", \"5\\n\", \"31\\n1\\n15\\n127\\n1\\n255\\n2097151\\n255\\n178481\\n\", \"21\\n\", \"31\\n1\\n15\\n127\\n255\\n127\\n2097151\\n255\\n16777215\\n\", \"3\\n\", \"31\\n1\\n7\\n127\\n1\\n31\\n2097151\\n255\\n16777215\\n\", \"31\\n1\\n7\\n127\\n255\\n127\\n2097151\\n255\\n2097151\\n\", \"31\\n7\\n7\\n127\\n255\\n255\\n2097151\\n255\\n16777215\\n\", \"511\\n\", \"5\\n7\\n15\\n127\\n1\\n127\\n2097151\\n85\\n178481\\n\", \"31\\n7\\n31\\n127\\n1\\n127\\n2097151\\n85\\n178481\\n\", \"31\\n7\\n15\\n127\\n1\\n127\\n2097151\\n127\\n178481\\n\", \"31\\n1\\n15\\n127\\n255\\n255\\n2097151\\n255\\n178481\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n131071\\n255\\n16777215\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n255\\n33554431\\n\", \"31\\n1\\n7\\n255\\n1\\n31\\n2097151\\n255\\n16777215\\n\", \"31\\n7\\n7\\n127\\n255\\n255\\n2097151\\n127\\n16777215\\n\", \"5\\n7\\n15\\n127\\n1\\n63\\n2097151\\n85\\n178481\\n\", \"31\\n7\\n31\\n127\\n255\\n127\\n2097151\\n85\\n178481\\n\", \"31\\n7\\n15\\n127\\n1\\n127\\n2097151\\n127\\n1048575\\n\", \"31\\n1\\n15\\n127\\n63\\n255\\n2097151\\n255\\n178481\\n\", \"31\\n1\\n31\\n127\\n1\\n127\\n131071\\n255\\n16777215\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n255\\n2097151\\n\", \"31\\n1\\n7\\n127\\n511\\n127\\n2097151\\n255\\n2097151\\n\", \"5\\n7\\n1\\n127\\n1\\n63\\n2097151\\n85\\n178481\\n\", \"5\\n1\\n15\\n127\\n1\\n63\\n1048575\\n85\\n178481\\n\", \"31\\n3\\n31\\n127\\n255\\n127\\n2097151\\n85\\n178481\\n\", \"31\\n7\\n15\\n127\\n1\\n127\\n2097151\\n127\\n262143\\n\", \"31\\n1\\n15\\n127\\n7\\n255\\n2097151\\n255\\n178481\\n\", \"31\\n1\\n15\\n127\\n255\\n127\\n2097151\\n255\\n2097151\\n\", \"31\\n7\\n7\\n127\\n255\\n511\\n2097151\\n127\\n16777215\\n\", \"31\\n7\\n7\\n127\\n255\\n255\\n2097151\\n255\\n8388607\\n\", \"31\\n3\\n63\\n127\\n255\\n127\\n2097151\\n85\\n178481\\n\", \"31\\n7\\n15\\n127\\n1\\n127\\n131071\\n255\\n16777215\\n\", \"31\\n15\\n15\\n127\\n255\\n127\\n2097151\\n255\\n16777215\\n\", \"31\\n1\\n1\\n127\\n255\\n127\\n2097151\\n255\\n2097151\\n\", \"31\\n7\\n7\\n127\\n255\\n511\\n4194303\\n127\\n16777215\\n\", \"31\\n7\\n7\\n255\\n255\\n255\\n2097151\\n255\\n8388607\\n\", \"5\\n1\\n15\\n255\\n1\\n63\\n1048575\\n85\\n178481\\n\", \"31\\n3\\n63\\n127\\n511\\n127\\n2097151\\n85\\n178481\\n\", \"15\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n255\\n178481\\n\", \"31\\n\", \"15\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n255\\n16777215\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n255\\n16777215\\n\", \"15\\n\", \"7\\n\", \"15\\n\", \"31\\n1\\n7\\n127\\n255\\n255\\n2097151\\n255\\n16777215\\n\", \"5\\n1\\n15\\n127\\n1\\n127\\n2097151\\n85\\n178481\\n\", \"127\\n\", \"1\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n255\\n16777215\\n\", \"31\\n1\\n15\\n127\\n1\\n127\\n2097151\\n255\\n16777215\\n\", \"15\\n\", \"7\\n\", \"31\\n\", \"31\\n1\\n7\\n127\\n255\\n255\\n2097151\\n255\\n16777215\\n\", \"63\\n\", \"5\\n1\\n15\\n127\\n1\\n127\\n1048575\\n85\\n178481\\n\", \"127\\n\", \"31\\n\", \"31\\n\", \"63\\n\", \"31\\n1\\n15\\n127\\n255\\n127\\n2097151\\n255\\n16777215\\n\", \"31\\n1\\n7\\n127\\n255\\n127\\n2097151\\n255\\n2097151\\n\", \"15\\n\", \"31\\n7\\n7\\n127\\n255\\n255\\n2097151\\n255\\n16777215\\n\", \"511\\n\", \"63\\n\", \"5\\n1\\n15\\n127\\n1\\n127\\n1048575\\n85\\n178481\\n\", \"63\\n\", \"31\\n\", \"127\\n\", \"31\\n1\\n15\\n127\\n255\\n127\\n2097151\\n255\\n16777215\\n\", \"31\\n7\\n7\\n127\\n255\\n255\\n2097151\\n127\\n16777215\\n\", \"31\\n\", \"31\\n7\\n7\\n127\\n255\\n255\\n2097151\\n255\\n16777215\\n\", \"511\\n\", \"63\\n\", \"127\\n\", \"63\\n\", \"3\\n1\\n7\\n\"]}", "source": "taco"}
|
Can the greatest common divisor and bitwise operations have anything in common? It is time to answer this question.
Suppose you are given a positive integer $a$. You want to choose some integer $b$ from $1$ to $a - 1$ inclusive in such a way that the greatest common divisor (GCD) of integers $a \oplus b$ and $a \> \& \> b$ is as large as possible. In other words, you'd like to compute the following function:
$$f(a) = \max_{0 < b < a}{gcd(a \oplus b, a \> \& \> b)}.$$
Here $\oplus$ denotes the bitwise XOR operation, and $\&$ denotes the bitwise AND operation.
The greatest common divisor of two integers $x$ and $y$ is the largest integer $g$ such that both $x$ and $y$ are divided by $g$ without remainder.
You are given $q$ integers $a_1, a_2, \ldots, a_q$. For each of these integers compute the largest possible value of the greatest common divisor (when $b$ is chosen optimally).
-----Input-----
The first line contains an integer $q$ ($1 \le q \le 10^3$) — the number of integers you need to compute the answer for.
After that $q$ integers are given, one per line: $a_1, a_2, \ldots, a_q$ ($2 \le a_i \le 2^{25} - 1$) — the integers you need to compute the answer for.
-----Output-----
For each integer, print the answer in the same order as the integers are given in input.
-----Example-----
Input
3
2
3
5
Output
3
1
7
-----Note-----
For the first integer the optimal choice is $b = 1$, then $a \oplus b = 3$, $a \> \& \> b = 0$, and the greatest common divisor of $3$ and $0$ is $3$.
For the second integer one optimal choice is $b = 2$, then $a \oplus b = 1$, $a \> \& \> b = 2$, and the greatest common divisor of $1$ and $2$ is $1$.
For the third integer the optimal choice is $b = 2$, then $a \oplus b = 7$, $a \> \& \> b = 0$, and the greatest common divisor of $7$ and $0$ is $7$.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"4 3 4\\nH 2\\nV 2\\nV 3\\nV 1\\n\", \"7 6 5\\nH 4\\nV 3\\nV 5\\nH 2\\nV 1\\n\", \"2 2 1\\nV 1\\n\", \"2 2 1\\nH 1\\n\", \"2 2 2\\nV 1\\nH 1\\n\", \"2 2 2\\nH 1\\nV 1\\n\", \"10 10 10\\nV 6\\nH 8\\nV 4\\nV 8\\nH 2\\nH 5\\nV 9\\nH 7\\nH 3\\nV 7\\n\", \"5 15 10\\nH 8\\nH 9\\nV 1\\nH 2\\nH 6\\nH 4\\nH 1\\nV 2\\nH 13\\nV 3\\n\", \"15 5 10\\nV 13\\nV 10\\nV 3\\nH 2\\nV 9\\nV 7\\nV 2\\nH 1\\nV 4\\nH 3\\n\", \"2 3 1\\nH 1\\n\", \"200000 200000 1\\nH 1\\n\", \"2 4 1\\nH 2\\n\", \"5 15 10\\nH 8\\nH 9\\nV 1\\nH 2\\nH 6\\nH 4\\nH 1\\nV 2\\nH 13\\nV 3\\n\", \"200000 200000 1\\nH 1\\n\", \"2 2 2\\nH 1\\nV 1\\n\", \"2 2 1\\nH 1\\n\", \"2 2 2\\nV 1\\nH 1\\n\", \"2 2 1\\nV 1\\n\", \"2 4 1\\nH 2\\n\", \"15 5 10\\nV 13\\nV 10\\nV 3\\nH 2\\nV 9\\nV 7\\nV 2\\nH 1\\nV 4\\nH 3\\n\", \"10 10 10\\nV 6\\nH 8\\nV 4\\nV 8\\nH 2\\nH 5\\nV 9\\nH 7\\nH 3\\nV 7\\n\", \"2 3 1\\nH 1\\n\", \"200000 108415 1\\nH 1\\n\", \"3 2 1\\nH 1\\n\", \"2 6 1\\nH 2\\n\", \"2 3 1\\nH 2\\n\", \"200000 108415 1\\nH 2\\n\", \"5 15 10\\nH 8\\nH 9\\nV 1\\nH 2\\nH 6\\nH 3\\nH 1\\nV 2\\nH 13\\nV 3\\n\", \"2 3 2\\nV 1\\nH 1\\n\", \"4 2 1\\nV 1\\n\", \"200000 88688 1\\nH 1\\n\", \"3 3 2\\nV 1\\nH 1\\n\", \"5 15 10\\nH 8\\nH 10\\nV 1\\nH 2\\nH 6\\nH 4\\nH 1\\nV 2\\nH 13\\nV 3\\n\", \"5 2 1\\nH 1\\n\", \"2 12 1\\nH 2\\n\", \"200000 160942 1\\nH 1\\n\", \"4 12 1\\nH 2\\n\", \"4 15 1\\nH 2\\n\", \"200000 200000 1\\nH 2\\n\", \"4 2 2\\nH 1\\nV 1\\n\", \"10 10 10\\nV 6\\nH 8\\nV 3\\nV 8\\nH 2\\nH 5\\nV 9\\nH 7\\nH 3\\nV 7\\n\", \"7 6 5\\nH 5\\nV 3\\nV 5\\nH 2\\nV 1\\n\", \"4 6 1\\nH 2\\n\", \"200000 98691 1\\nH 2\\n\", \"9 2 1\\nH 1\\n\", \"4 13 1\\nH 2\\n\", \"4 24 1\\nH 2\\n\", \"200000 55054 1\\nH 2\\n\", \"4 3 2\\nH 1\\nV 1\\n\", \"4 4 1\\nH 1\\n\", \"200000 98691 1\\nH 4\\n\", \"5 30 10\\nH 8\\nH 9\\nV 1\\nH 2\\nH 5\\nH 3\\nH 1\\nV 2\\nH 13\\nV 3\\n\", \"4 10 1\\nH 2\\n\", \"4 24 1\\nH 1\\n\", \"174568 55054 1\\nH 2\\n\", \"7 4 1\\nH 1\\n\", \"200000 98691 1\\nH 7\\n\", \"7 7 1\\nH 1\\n\", \"3 7 1\\nH 2\\n\", \"6 7 1\\nH 1\\n\", \"2 4 1\\nH 1\\n\", \"4 2 1\\nH 1\\n\", \"6 2 1\\nH 1\\n\", \"4 3 1\\nH 1\\n\", \"3 3 1\\nH 1\\n\", \"5 15 10\\nH 8\\nH 9\\nV 1\\nH 2\\nH 5\\nH 3\\nH 1\\nV 2\\nH 13\\nV 3\\n\", \"3 6 1\\nH 2\\n\", \"4 7 1\\nH 2\\n\", \"4 3 4\\nH 2\\nV 2\\nV 3\\nV 1\\n\", \"7 6 5\\nH 4\\nV 3\\nV 5\\nH 2\\nV 1\\n\"], \"outputs\": [\"8\\n4\\n4\\n2\\n\", \"28\\n16\\n12\\n6\\n4\\n\", \"2\\n\", \"2\\n\", \"2\\n1\\n\", \"2\\n1\\n\", \"60\\n48\\n32\\n32\\n24\\n12\\n12\\n12\\n8\\n8\\n\", \"40\\n40\\n32\\n24\\n24\\n24\\n24\\n18\\n12\\n8\\n\", \"65\\n50\\n35\\n21\\n18\\n12\\n12\\n12\\n9\\n6\\n\", \"4\\n\", \"39999800000\\n\", \"4\\n\", \"40\\n40\\n32\\n24\\n24\\n24\\n24\\n18\\n12\\n8\\n\", \"39999800000\\n\", \"2\\n1\\n\", \"2\\n\", \"2\\n1\\n\", \"2\\n\", \"4\\n\", \"65\\n50\\n35\\n21\\n18\\n12\\n12\\n12\\n9\\n6\\n\", \"60\\n48\\n32\\n32\\n24\\n12\\n12\\n12\\n8\\n8\\n\", \"4\\n\", \"21682800000\\n\", \"3\\n\", \"8\\n\", \"4\\n\", \"21682600000\\n\", \"40\\n40\\n32\\n24\\n24\\n24\\n24\\n18\\n12\\n8\\n\", \"3\\n2\\n\", \"6\\n\", \"17737400000\\n\", \"6\\n4\\n\", \"40\\n40\\n32\\n24\\n20\\n20\\n20\\n15\\n9\\n6\\n\", \"5\\n\", \"20\\n\", \"32188200000\\n\", \"40\\n\", \"52\\n\", \"39999600000\\n\", \"4\\n3\\n\", \"60\\n48\\n32\\n24\\n18\\n9\\n9\\n9\\n6\\n6\\n\", \"35\\n20\\n15\\n9\\n6\\n\", \"16\\n\", \"19737800000\\n\", \"9\\n\", \"44\\n\", \"88\\n\", \"11010400000\\n\", \"8\\n6\\n\", \"12\\n\", \"19737400000\\n\", \"110\\n105\\n84\\n84\\n84\\n84\\n84\\n63\\n51\\n34\\n\", \"32\\n\", \"92\\n\", \"9610317536\\n\", \"21\\n\", \"19736800000\\n\", \"42\\n\", \"15\\n\", \"36\\n\", \"6\\n\", \"4\\n\", \"6\\n\", \"8\\n\", \"6\\n\", \"40\\n40\\n32\\n24\\n24\\n24\\n24\\n18\\n12\\n8\\n\", \"12\\n\", \"20\\n\", \"8\\n4\\n4\\n2\\n\", \"28\\n16\\n12\\n6\\n4\\n\"]}", "source": "taco"}
|
Leonid wants to become a glass carver (the person who creates beautiful artworks by cutting the glass). He already has a rectangular w mm × h mm sheet of glass, a diamond glass cutter and lots of enthusiasm. What he lacks is understanding of what to carve and how.
In order not to waste time, he decided to practice the technique of carving. To do this, he makes vertical and horizontal cuts through the entire sheet. This process results in making smaller rectangular fragments of glass. Leonid does not move the newly made glass fragments. In particular, a cut divides each fragment of glass that it goes through into smaller fragments.
After each cut Leonid tries to determine what area the largest of the currently available glass fragments has. Since there appear more and more fragments, this question takes him more and more time and distracts him from the fascinating process.
Leonid offers to divide the labor — he will cut glass, and you will calculate the area of the maximum fragment after each cut. Do you agree?
-----Input-----
The first line contains three integers w, h, n (2 ≤ w, h ≤ 200 000, 1 ≤ n ≤ 200 000).
Next n lines contain the descriptions of the cuts. Each description has the form H y or V x. In the first case Leonid makes the horizontal cut at the distance y millimeters (1 ≤ y ≤ h - 1) from the lower edge of the original sheet of glass. In the second case Leonid makes a vertical cut at distance x (1 ≤ x ≤ w - 1) millimeters from the left edge of the original sheet of glass. It is guaranteed that Leonid won't make two identical cuts.
-----Output-----
After each cut print on a single line the area of the maximum available glass fragment in mm^2.
-----Examples-----
Input
4 3 4
H 2
V 2
V 3
V 1
Output
8
4
4
2
Input
7 6 5
H 4
V 3
V 5
H 2
V 1
Output
28
16
12
6
4
-----Note-----
Picture for the first sample test: [Image] Picture for the second sample test: $\square$
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.25
|
{"tests": "{\"inputs\": [\"2\\n3\\n4\", \"2\\n1\\n4\", \"2\\n2\\n4\", \"2\\n2\\n1\", \"2\\n1\\n1\", \"2\\n4\\n4\", \"2\\n5\\n4\", \"2\\n1\\n6\", \"2\\n-1\\n4\", \"2\\n6\\n4\", \"2\\n4\\n1\", \"2\\n-1\\n7\", \"2\\n6\\n2\", \"2\\n6\\n1\", \"2\\n-1\\n8\", \"2\\n6\\n3\", \"2\\n10\\n1\", \"2\\n4\\n3\", \"2\\n1\\n7\", \"2\\n3\\n7\", \"2\\n3\\n3\", \"2\\n2\\n8\", \"2\\n7\\n4\", \"2\\n2\\n7\", \"2\\n2\\n2\", \"2\\n10\\n4\", \"2\\n12\\n4\", \"2\\n5\\n1\", \"2\\n-1\\n2\", \"2\\n6\\n6\", \"2\\n13\\n1\", \"2\\n2\\n3\", \"2\\n3\\n13\", \"2\\n1\\n3\", \"2\\n7\\n1\", \"2\\n2\\n14\", \"2\\n1\\n2\", \"2\\n12\\n7\", \"2\\n5\\n2\", \"2\\n-1\\n3\", \"2\\n13\\n2\", \"2\\n8\\n3\", \"2\\n3\\n5\", \"2\\n3\\n14\", \"2\\n2\\n11\", \"2\\n2\\n6\", \"2\\n12\\n12\", \"2\\n-1\\n1\", \"2\\n5\\n3\", \"2\\n1\\n5\", \"2\\n2\\n22\", \"2\\n18\\n12\", \"2\\n-2\\n2\", \"2\\n5\\n5\", \"2\\n4\\n2\", \"2\\n1\\n22\", \"2\\n18\\n18\", \"2\\n5\\n10\", \"2\\n18\\n15\", \"2\\n3\\n2\", \"2\\n-1\\n-1\", \"2\\n4\\n6\", \"2\\n5\\n6\", \"2\\n1\\n12\", \"2\\n2\\n10\", \"2\\n-1\\n5\", \"2\\n7\\n6\", \"2\\n9\\n-1\", \"2\\n9\\n1\", \"2\\n3\\n1\", \"2\\n-2\\n3\", \"2\\n-2\\n8\", \"2\\n11\\n4\", \"2\\n9\\n4\", \"2\\n6\\n7\", \"2\\n3\\n-1\", \"2\\n4\\n8\", \"2\\n-3\\n3\", \"2\\n16\\n4\", \"2\\n12\\n6\", \"2\\n8\\n4\", \"2\\n-1\\n-2\", \"2\\n6\\n9\", \"2\\n2\\n5\", \"2\\n4\\n13\", \"2\\n19\\n1\", \"2\\n4\\n14\", \"2\\n4\\n7\", \"2\\n-2\\n1\", \"2\\n-4\\n-1\", \"2\\n2\\n-1\", \"2\\n5\\n7\", \"2\\n8\\n6\", \"2\\n3\\n6\", \"2\\n2\\n12\", \"2\\n2\\n9\", \"2\\n19\\n12\", \"2\\n-3\\n6\", \"2\\n7\\n3\", \"2\\n1\\n-1\", \"2\\n2\\n38\", \"2\\n3\\n4\"], \"outputs\": [\"NO\\nYES\", \"NO\\nYES\\n\", \"YES\\nYES\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nYES\\n\", \"NO\\nYES\\n\", \"NO\\nYES\\n\", \"NO\\nYES\\n\", \"YES\\nYES\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nYES\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nYES\\n\", \"YES\\nNO\\n\", \"YES\\nYES\\n\", \"NO\\nYES\\n\", \"YES\\nYES\\n\", \"NO\\nNO\\n\", \"NO\\nYES\\n\", \"YES\\nYES\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nYES\\n\", \"YES\\nNO\\n\", \"NO\\nYES\\n\", \"NO\\nNO\\n\", \"NO\\nYES\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"YES\\nYES\\n\", \"YES\\nYES\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nYES\\n\", \"NO\\nYES\\n\", \"NO\\nNO\\n\", \"YES\\nYES\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nYES\\n\", \"NO\\nNO\\n\", \"YES\\nYES\\n\", \"NO\\nYES\\n\", \"NO\\nYES\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nYES\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nYES\\n\", \"NO\\nYES\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nYES\\n\", \"YES\\nYES\\n\", \"NO\\nYES\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"YES\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nNO\\n\", \"NO\\nYES\\n\", \"NO\\nYES\\n\", \"YES\\nYES\\n\", \"YES\\nNO\\n\", \"NO\\nYES\\n\", \"NO\\nYES\\n\", \"NO\\nNO\\n\", \"NO\\nNO\\n\", \"YES\\nNO\\n\", \"NO\\nYES\\n\"]}", "source": "taco"}
|
Asmany strings are strings of '0's and '1's that have as many 00 as 11. A string such as 00110001 consists of 3 "00" and
1 "11". Of course this is not an Asmany string. 0011, 1100, 000111000111 are Asmany strings. An L'th Asmany number is the number of
Asmany strings of length L for all positive integers L.
For esoteric purposes Chef had an oracle (a device) that was capable of answering whether a number that he entered was an Asmany number.
The problem is that his oracle takes too long for large numbers. Him being Chef, he wants to ask the oracle very
large numbers! You tell him that you can give him a better oracle (a program) that will tell him what he wants to know in the blink of
an eye.
------ Input ------
The first Line contains a single number T, the number of test cases.
Each test case contains 1 positive integer N, with not more than 1000 digits.
------ Output ------
Print YES if N is an Asmany number, NO otherwise.
------ Constraints ------
1 ≤ T ≤ 100
1 ≤ Number of digits in N ≤ 1000
------ Sample Input ------
2
3
4
------ Sample Output ------
NO
YES
------ Explanation ------
4 is an Asmany number. To be precise, it is the 4th Asmany number: There are 4 Asmany strings of length 4. 0011, 1100, 0101, 1010.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
{"tests": "{\"inputs\": [\"3\\n1 2 3\\n\", \"3\\n3 1 2\\n\", \"1\\n13\\n\", \"10\\n67 67 67 67 67 67 67 67 67 67\\n\", \"10\\n16 17 16 15 14 15 16 17 16 15\\n\", \"4\\n54 54 54 55\\n\", \"3\\n68 67 67\\n\", \"5\\n46 46 47 46 45\\n\", \"4\\n14 15 15 16\\n\", \"6\\n59 59 60 60 59 58\\n\", \"3\\n40 40 40\\n\", \"4\\n90 91 90 91\\n\", \"10\\n9 9 9 10 10 9 8 8 9 9\\n\", \"3\\n22 23 24\\n\", \"9\\n71 71 70 70 71 70 69 70 71\\n\", \"9\\n15 14 14 13 13 12 13 13 14\\n\", \"4\\n61 60 60 60\\n\", \"4\\n16 17 17 18\\n\", \"6\\n87 86 86 86 85 86\\n\", \"5\\n64 63 63 62 61\\n\", \"9\\n13 80 13 38 98 85 11 73 74\\n\", \"10\\n2 83 18 65 58 95 37 51 86 47\\n\", \"6\\n47 100 96 2 96 43\\n\", \"10\\n28 61 23 73 61 33 45 55 18 43\\n\", \"10\\n95 51 52 8 44 39 77 17 96 88\\n\", \"5\\n14 91 91 91 84\\n\", \"4\\n92 18 29 93\\n\", \"7\\n23 37 39 8 72 31 85\\n\", \"4\\n61 28 3 81\\n\", \"4\\n83 100 81 75\\n\", \"9\\n95 7 97 61 90 7 30 65 39\\n\", \"3\\n90 39 98\\n\", \"3\\n76 9 12\\n\", \"3\\n69 26 73\\n\", \"10\\n55 39 93 42 97 40 36 38 11 97\\n\", \"5\\n21 57 40 94 17\\n\", \"7\\n35 91 87 78 17 71 63\\n\", \"7\\n20 21 95 73 49 98 53\\n\", \"8\\n46 4 30 85 52 6 84 13\\n\", \"10\\n79 84 22 38 23 22 33 42 13 96\\n\", \"4\\n90 91 90 91\\n\", \"4\\n54 54 54 55\\n\", \"10\\n55 39 93 42 97 40 36 38 11 97\\n\", \"3\\n90 39 98\\n\", \"5\\n21 57 40 94 17\\n\", \"8\\n46 4 30 85 52 6 84 13\\n\", \"6\\n47 100 96 2 96 43\\n\", \"4\\n61 28 3 81\\n\", \"5\\n14 91 91 91 84\\n\", \"3\\n22 23 24\\n\", \"1\\n13\\n\", \"9\\n13 80 13 38 98 85 11 73 74\\n\", \"10\\n95 51 52 8 44 39 77 17 96 88\\n\", \"3\\n40 40 40\\n\", \"4\\n16 17 17 18\\n\", \"3\\n68 67 67\\n\", \"4\\n83 100 81 75\\n\", \"9\\n71 71 70 70 71 70 69 70 71\\n\", \"10\\n9 9 9 10 10 9 8 8 9 9\\n\", \"6\\n87 86 86 86 85 86\\n\", \"5\\n64 63 63 62 61\\n\", \"3\\n76 9 12\\n\", \"4\\n61 60 60 60\\n\", \"7\\n23 37 39 8 72 31 85\\n\", \"10\\n67 67 67 67 67 67 67 67 67 67\\n\", \"4\\n92 18 29 93\\n\", \"4\\n14 15 15 16\\n\", \"10\\n79 84 22 38 23 22 33 42 13 96\\n\", \"7\\n20 21 95 73 49 98 53\\n\", \"10\\n28 61 23 73 61 33 45 55 18 43\\n\", \"9\\n15 14 14 13 13 12 13 13 14\\n\", \"5\\n46 46 47 46 45\\n\", \"7\\n35 91 87 78 17 71 63\\n\", \"3\\n69 26 73\\n\", \"10\\n16 17 16 15 14 15 16 17 16 15\\n\", \"9\\n95 7 97 61 90 7 30 65 39\\n\", \"10\\n2 83 18 65 58 95 37 51 86 47\\n\", \"6\\n59 59 60 60 59 58\\n\", \"4\\n90 91 83 91\\n\", \"1\\n17\\n\", \"4\\n59 54 54 55\\n\", \"10\\n55 39 93 63 97 40 36 38 11 97\\n\", \"5\\n21 57 40 94 0\\n\", \"8\\n86 4 30 85 52 6 84 13\\n\", \"6\\n47 110 96 2 96 43\\n\", \"4\\n61 28 4 81\\n\", \"5\\n14 91 91 91 0\\n\", \"3\\n22 6 24\\n\", \"9\\n13 80 13 38 98 85 11 73 30\\n\", \"10\\n95 51 52 8 44 39 60 17 96 88\\n\", \"3\\n47 40 40\\n\", \"4\\n83 110 81 75\\n\", \"10\\n9 9 4 10 10 9 8 8 9 9\\n\", \"3\\n30 9 12\\n\", \"4\\n61 49 60 60\\n\", \"7\\n23 37 46 8 72 31 85\\n\", \"4\\n92 26 29 93\\n\", \"10\\n79 84 22 29 23 22 33 42 13 96\\n\", \"7\\n20 21 95 73 49 153 53\\n\", \"10\\n28 61 23 73 61 62 45 55 18 43\\n\", \"5\\n46 86 47 46 45\\n\", \"7\\n35 91 87 85 17 71 63\\n\", \"3\\n65 26 73\\n\", \"10\\n16 17 16 4 14 15 16 17 16 15\\n\", \"9\\n95 8 97 61 90 7 30 65 39\\n\", \"10\\n2 83 18 65 58 44 37 51 86 47\\n\", \"6\\n59 59 60 59 59 58\\n\", \"3\\n2 1 2\\n\", \"3\\n1 2 1\\n\", \"4\\n90 30 83 91\\n\", \"10\\n105 39 93 63 97 40 36 38 11 97\\n\", \"5\\n21 94 40 94 0\\n\", \"8\\n86 4 30 85 98 6 84 13\\n\", \"6\\n47 110 178 2 96 43\\n\", \"4\\n3 28 4 81\\n\", \"5\\n14 91 91 91 1\\n\", \"3\\n41 6 24\\n\", \"1\\n7\\n\", \"9\\n13 80 13 38 98 85 11 79 30\\n\", \"10\\n95 51 0 8 44 39 60 17 96 88\\n\", \"3\\n66 40 40\\n\", \"4\\n83 110 81 47\\n\", \"10\\n9 9 4 10 10 9 10 8 9 9\\n\", \"3\\n46 9 12\\n\", \"7\\n23 37 46 3 72 31 85\\n\", \"4\\n92 26 29 65\\n\", \"10\\n79 91 22 29 23 22 33 42 13 96\\n\", \"7\\n20 21 95 73 49 153 103\\n\", \"10\\n28 61 41 73 61 62 45 55 18 43\\n\", \"5\\n46 78 47 46 45\\n\", \"7\\n35 91 87 85 17 106 63\\n\", \"3\\n72 26 73\\n\", \"10\\n16 17 16 4 14 15 16 7 16 15\\n\", \"9\\n95 8 97 61 90 7 30 128 39\\n\", \"10\\n2 83 18 65 58 44 37 13 86 47\\n\", \"6\\n59 59 60 20 59 58\\n\", \"3\\n3 0 2\\n\", \"3\\n1 4 1\\n\", \"4\\n90 16 83 91\\n\", \"10\\n105 39 79 63 97 40 36 38 11 97\\n\", \"5\\n21 94 40 161 0\\n\", \"8\\n86 6 30 85 98 6 84 13\\n\", \"6\\n47 100 178 2 96 43\\n\", \"4\\n3 28 0 81\\n\", \"5\\n14 91 91 0 1\\n\", \"3\\n41 5 24\\n\", \"1\\n14\\n\", \"9\\n13 80 22 38 98 85 11 79 30\\n\", \"10\\n95 51 0 8 44 39 60 16 96 88\\n\", \"3\\n66 40 68\\n\", \"4\\n83 110 97 47\\n\", \"3\\n62 9 12\\n\", \"7\\n23 37 76 3 72 31 85\\n\", \"4\\n92 26 29 122\\n\", \"10\\n109 91 22 29 23 22 33 42 13 96\\n\", \"7\\n20 21 74 73 49 153 103\\n\", \"10\\n1 61 41 73 61 62 45 55 18 43\\n\", \"7\\n35 91 87 85 6 106 63\\n\", \"3\\n72 16 73\\n\", \"10\\n16 17 16 7 14 15 16 7 16 15\\n\", \"9\\n95 8 97 45 90 7 30 128 39\\n\", \"10\\n2 83 18 65 58 44 37 13 86 33\\n\", \"6\\n59 59 60 20 59 91\\n\", \"3\\n3 0 4\\n\", \"3\\n1 6 1\\n\", \"4\\n90 16 155 91\\n\", \"10\\n105 15 79 63 97 40 36 38 11 97\\n\", \"5\\n21 94 40 139 0\\n\", \"8\\n41 6 30 85 98 6 84 13\\n\", \"6\\n47 100 178 2 96 82\\n\", \"4\\n3 28 1 81\\n\", \"5\\n14 130 91 0 1\\n\", \"3\\n41 5 17\\n\", \"1\\n18\\n\", \"9\\n13 80 22 23 98 85 11 79 30\\n\", \"10\\n95 51 0 8 44 52 60 16 96 88\\n\", \"3\\n66 36 68\\n\", \"4\\n80 110 97 47\\n\", \"3\\n3 1 2\\n\", \"3\\n1 2 3\\n\"], \"outputs\": [\"YES\\n\", \"NO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\", \"YES\", \"NO\", \"NO\", \"NO\", \"NO\", \"NO\", \"NO\", \"NO\", \"YES\", \"YES\", \"NO\", \"NO\", \"YES\", \"YES\", \"YES\", \"NO\", \"YES\", \"YES\", \"YES\", \"YES\", \"NO\", \"YES\", \"NO\", \"YES\", \"NO\", \"YES\", \"NO\", \"NO\", \"NO\", \"YES\", \"YES\", \"NO\", \"NO\", \"YES\", \"NO\", \"NO\", \"YES\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"YES\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"YES\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\\n\", \"NO\", \"YES\"]}", "source": "taco"}
|
Everybody knows of spaghetti sort. You decided to implement an analog sorting algorithm yourself, but as you survey your pantry you realize you're out of spaghetti! The only type of pasta you have is ravioli, but you are not going to let this stop you...
You come up with the following algorithm. For each number in the array a_{i}, build a stack of a_{i} ravioli. The image shows the stack for a_{i} = 4.
[Image]
Arrange the stacks in one row in the order in which the corresponding numbers appear in the input array. Find the tallest one (if there are several stacks of maximal height, use the leftmost one). Remove it and add its height to the end of the output array. Shift the stacks in the row so that there is no gap between them. Repeat the procedure until all stacks have been removed.
At first you are very happy with your algorithm, but as you try it on more inputs you realize that it doesn't always produce the right sorted array. Turns out when two stacks of ravioli are next to each other (at any step of the process) and differ in height by two or more, the top ravioli of the taller stack slides down on top of the lower stack.
Given an input array, figure out whether the described algorithm will sort it correctly.
-----Input-----
The first line of input contains a single number n (1 ≤ n ≤ 10) — the size of the array.
The second line of input contains n space-separated integers a_{i} (1 ≤ a_{i} ≤ 100) — the elements of the array.
-----Output-----
Output "YES" if the array can be sorted using the described procedure and "NO" if it can not.
-----Examples-----
Input
3
1 2 3
Output
YES
Input
3
3 1 2
Output
NO
-----Note-----
In the second example the array will change even before the tallest stack is chosen for the first time: ravioli from stack of height 3 will slide on the stack of height 1, and the algorithm will output an array {2, 2, 2}.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0.125
|
{"tests": "{\"inputs\": [\"5\\n2 3\\n1 2 3\\n1 1 1\\n2 2\\n4 1\\n2 3\\n2 2\\n2 1\\n1 1\\n2 3\\n6 2 1\\n5 4 3\\n2 1\\n1\\n2\\n\", \"1\\n1 7\\n1 2 4 3 3 3 5\\n\", \"4\\n1 10\\n1 2 3 2 2 2 2 2 3 3\\n1 10\\n1 2 3 3 3 3 3 2 3 3\\n1 10\\n1 2 3 3 3 3 2 2 3 3\\n1 5\\n1 4 3 2 5\\n\", \"1\\n2 4\\n2 1 1 1\\n2 2 2 1\\n\", \"1\\n1 5\\n1 2 4 3 3\\n\", \"1\\n1 5\\n1 3 2 2 4\\n\", \"1\\n1 3\\n2 1 1\\n\"], \"outputs\": [\"1 1\\n-1\\n1 2\\n1 3\\n1 1\\n\", \"3 6\\n\", \"3 8\\n3 8\\n-1\\n2 4\\n\", \"1 4\\n\", \"3 5\\n\", \"2 4\\n\", \"1 3\\n\"]}", "source": "taco"}
|
You are given a grid with $n$ rows and $m$ columns, where each cell has a positive integer written on it. Let's call a grid good, if in each row the sequence of numbers is sorted in a non-decreasing order. It means, that for each $1 \le i \le n$ and $2 \le j \le m$ the following holds: $a_{i,j} \ge a_{i, j-1}$.
You have to to do the following operation exactly once: choose two columns with indexes $i$ and $j$ (not necessarily different), $1 \le i, j \le m$, and swap them.
You are asked to determine whether it is possible to make the grid good after the swap and, if it is, find the columns that need to be swapped.
-----Input-----
Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 100$). Description of the test cases follows.
The first line of each test case contains two integers $n$ and $m$ ($1 \le n, m \le 2 \cdot 10^5$) — the number of rows and columns respectively.
Each of the next $n$ rows contains $m$ integers, $j$-th element of $i$-th row is $a_{i,j}$ ($1 \le a_{i,j} \le 10^9$) — the number written in the $j$-th cell of the $i$-th row.
It's guaranteed that the sum of $n \cdot m$ over all test cases does not exceed $2 \cdot 10^5$.
-----Output-----
If after the swap it is impossible to get a good grid, output $-1$.
In the other case output $2$ integers — the indices of the columns that should be swapped to get a good grid.
If there are multiple solutions, print any.
-----Examples-----
Input
5
2 3
1 2 3
1 1 1
2 2
4 1
2 3
2 2
2 1
1 1
2 3
6 2 1
5 4 3
2 1
1
2
Output
1 1
-1
1 2
1 3
1 1
-----Note-----
In the first test case the grid is initially good, so we can, for example, swap the first column with itself.
In the second test case it is impossible to make the grid good.
In the third test case it is needed to swap the first and the second column, then the grid becomes good.
Read the inputs from stdin solve the problem and write the answer to stdout (do not directly test on the sample inputs). Enclose your code within ```python delimiters.
| 0
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.